Journal List > Nat Prod Sci > v.24(3) > 1102536

TOOLS
Lee, Kang, Kim, Kim, and Sung: Classficiation of Bupleuri Radix according to Geographical Origins using Near Infrared Spectroscopy (NIRS) Combined with Supervised Pattern Recognition
Original Article

Natural Product Sciences 2018;24(3):164-170.

Published online: 17 January 2018

DOI: https://doi.org/10.20307/nps.2018.24.3.164

Classficiation of Bupleuri Radix according to Geographical Origins using Near Infrared Spectroscopy (NIRS) Combined with Supervised Pattern Recognition

Dong Young Lee1, Kyo Bin Kang2, Jina Kim1, Hyo Jin Kim3, Sang Hyun Sung1

1College of Pharmacy and Research Institute of Pharmaceutical Science, Seoul National University, Seoul 151-742, Republic of Korea

2College of Pharmacy, Sookmyung Women's University, Seoul 04310, Republic of Korea

3College of Pharmacy, Dongduk Women's University, Seoul 136-714, Republic of Korea

∗Author for correspondence Sang Hyun Sung, College of Pharmacy and Research Institute of Pharmaceutical Science, Seoul National University, Seoul 151-742, Republic of Korea. Tel: +82-2-880-7859; E-mail: shsung@snu.ac.kr

Received 18 December 2017       Revised 3 April 2018       Accepted 4 April 2018

Copyright © 2018 The Korean Society of Pharmacognosy

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

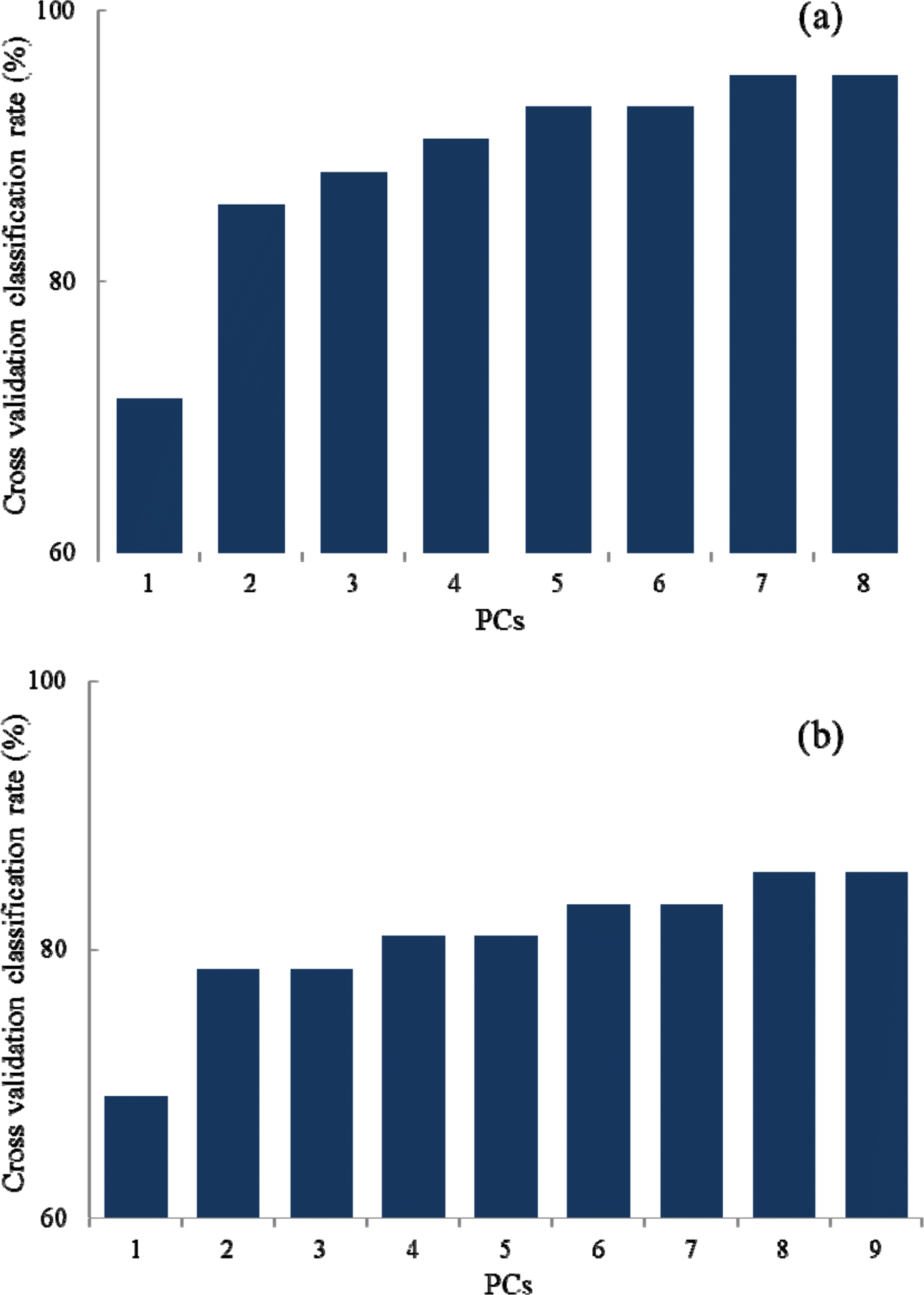
Rapid geographical classification of Bupleuri Radix is important in quality control. In this study, near infrared spectroscopy (NIRS) combined with supervised pattern recognition was attempted to classify Bupleuri Radix according to geographical origins. Three supervised pattern recognitions methods, partial least square discriminant analysis (PLS-DA), quadratic discriminant analysis (QDA) and radial basis function support vector machine (RBF-SVM), were performed to establish the classification models. The QDA and RBF-SVM models were performed based on principal component analysis (PCA). The number of principal components (PCs) was optimized by cross-validation in the model. The results showed that the performance of the QDA model is the optimum among the three models. The optimized QDA model was obtained when 7 PCs were used; the classification rates of the QDA model in the training and test sets are 97.8% and 95.2% respectively. The overall results showed that NIRS combined with supervised pattern recognition could be applied to classify Bupleuri Radix according to geographical origin.

Keywords: Near infrared spectroscopy, Bupleuri Radix, Geographical classification, Supervised pattern recognition

REFERENCES

(1). Ashour M. L., Wink M. J.Pharm. Pharmacol. 2011; 63:305–321.
(2). Bermejo Benito P., Abad Martínez M. J., Silván Sen A. M., Sanz Gómez A., Fernández Matellano L., Sánchez Contreras S., Díaz Lanza A. M.Life Sci. 1998; 63:1147–1156.
(3). Cheng X. Q., Li H., Yue X. L., Xie J. Y., Zhang Y. Y., Di H. Y., Chen D. F. J.Ethnopharmacol. 2010; 130:363–368.
(4). Sun X. B., Matsumoto T., Yamada H. J.Pharm. Pharmacol. 1991; 43:699–704.
(5). Wen S., Huifu X., Hao H.Immunopharmacol. Immunotoxicol. 2011; 33:433–437.
(6). Zhu L., Liang Z. T., Yi T., Ma Y., Zhao Z. Z., Guo B. L., Zhang J. Y., Chen H. B.BMC Complement. Altern. Med. 2017; 17:305–316.
(7). Li X., Jia Y., Song A., Chen X., Bi K.Yakugaku Zasshi. 2005; 125:815–819.
(8). Bao Y., Li C., Shen H., Nan F.Anal. Chem. 2004; 76:4208–4216.
(9). Liau B. C., Hsiao S. S., Lee M. R., Jong T. T., Chiang S. T. J.Pharm. Biomed. Anal. 2007; 43:1174–1178.
(10). Lee J., Yang D. H., Suh J. H., Kim U., Eom H. Y., Kim J., Lee M. Y., Kim J., Han S. B. J. Chromatogr. B.Analyt. Technol. Biomed. Life Sci. 2011; 879:3887–3895.
(11). Huang H. Q., Su J., Zhang X., Shan L., Zhang W. D. J.Chromatogr. A. 2011; 1218:1131–1138.
(12). Tian R. T., Xie P. S., Liu H. P. J.Chromatogr. A. 2009; 1216:2150–2155.
(13). Qin X., Dai Y., Liu N. Q., Li Z., Liu X., Hu J., Choi Y. H., Verpoorte R.Planta Med. 2012; 78:926–933.
(14). Lin X., Xue L., Zhang H., Zhu C.Anal. Bioanal. Chem. 2005; 382:1610–1615.
(15). Gong F., Wang B. T., Chau F. T., Liang Y. Z.Anal. Lett. 2005; 38:2475–2492.
(16). McGoverin C. M., Weeranantanaphan J., Downey G., Manley M. J.Near Infrared Spec. 2010; 18:87–111.
(17). Chen Y., Xie M. Y., Yan Y., Zhu S. B., Nie S. P., Li C., Wang Y. X., Gong X. F.Anal. Chim. Acta. 2008; 618:121–130.
(18). Luo X. F., Yu, X.;Wu, X. M.;Cheng, H. B.;Qu H. B.Microchem. J. 2008; 90:8–12.
(19). Wang L., Lee F. S. C., Wang X.LWT-Food Sci. Technol. 2007; 40:83–88.
(20). Chen Q., Zhao J., Lin H. Spectrochim.Acta A. Mol. Biomol. Spectrosc. 2009; 72:845–850.
(21). Lin H., Zhao J., Chen Q., Zhou F., Sun L. Spectrochim Acta. A.Mol. Biomol. Spectrosc. 2011; 79:1381–1385.
(22). Lee D. Y., Kim S. H., Kim Y. C., Kim H. J., Sung S. H.Microchem. J. 2011; 99:213–217.
(23). Berrueta L. A., Alonso-Salces R. M., Héberger K.J. Chromatogr. A. 2007; 1158:196–214.
(24). Li B., Wei Y., Duan H., Xi L., Wu X.Vib. Spectrosc. 2012; 62:17–22.
(25). Chiang L. H., Russell E. L., Braatz R. D.Chemometrics Intell. Lab. Syst. 2000; 50:243–252.
(26). Jiang H., Liu G. H., Xiao X., Yu S., Mei C., Ding Y.Food Anal. Methods. 2012; 5:928–934.
(27). Luts J., Ojeda F., Van de Plas R., De Moor B., Van Huffel S., Suykens J. A.Anal. Chim. Acta. 2010; 665:129–145.
(28). Ballabio D., Consonni V.Anal. Methods. 2013; 5:3790–3798.
(29). Rubin T. N., Chambers A., Smyth P., Steyvers M.Mach. Learn. 2012; 88:157–208.

Fig. 1.
Average NIR reflectance specrtra of Bupleuri Radix obtained from raw data.
nps-24-164f1.tif
Fig. 2.
Average NIR reflectance specrtra of Bupleuri Radix with 2nd derivative preprocessing.
nps-24-164f2.tif
Fig. 3.
Two dimensional score plot of the top two principal components (PCs) for all samples.
nps-24-164f3.tif
Fig. 4.
Cross validation classification rates of QDA (a) and RBF-SVM (b) models at different PCs.
nps-24-164f4.tif
Table 1.
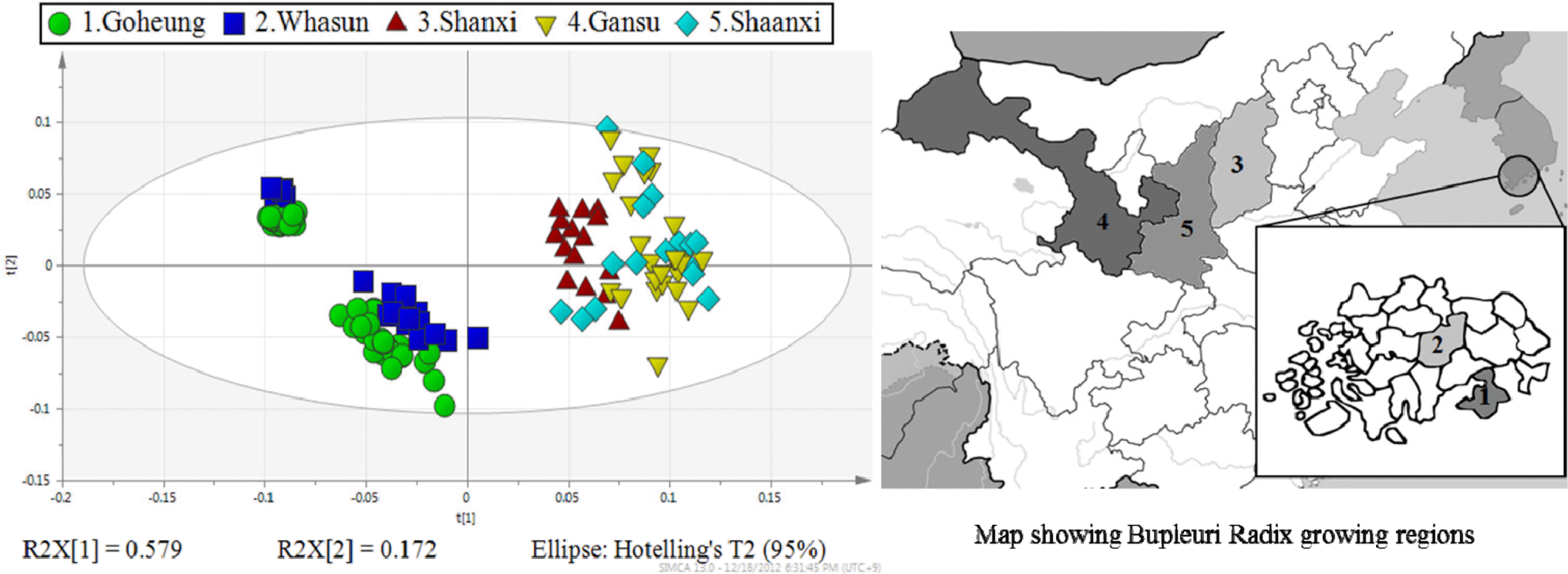
Summary of testing Bupleuri Radix samples
Geographical origins Number of samples
Training set Test set
South Korea
　 Goheung 35 17
　 Whasun 16 7
China
　 Shanxi 10 5
　 Gansu 17 8
　 Shaanxi 11 5
Table 2.
Classification results by PLS-DA model
PLS-DA Goheung Whasun Shanxi Gansu Shaanxi Classification rate (%)
per group all groups
Training set (n=89) Goheung 35 0 0 0 0 100 83.3
Whasun 0 16 0 0 0 100
Shanxi 0 0 8 0 2 80
Gansu 0 0 0 17 0 100
Shaanxi 1 0 0 7 3 27.3
Test set (n=42) Goheung 17 0 0 0 0 100 88.8
Whasun 0 7 0 0 0 100
Shanxi 0 0 2 0 3 40
Gansu 0 0 0 8 0 100
Shaanxi 0 0 0 4 1 20

∗The rows indicate the true sample class and that the columns refer to the observed class.

Table 3.
Classification results by QDA model
QDA Goheung Whasun Shanxi Gansu Shaanxi Classification rate (%)
per group all groups
Training set (n=89) Goheung 35 0 0 0 0 100 97.8
Whasun 0 16 0 0 0 100
Shanxi 0 0 10 0 0 100
Gansu 0 0 0 17 0 100
Shaanxi 0 0 0 2 9 81.8
Test set (n=42) Goheung 17 0 0 0 0 100 95.2
Whasun 0 7 0 0 0 100
Shanxi 0 0 5 0 0 100
Gansu 0 0 0 8 0 100
Shaanxi 0 0 0 2 3 60

∗ The rows indicate the true sample class and that the columns refer to the observed class.

Table 4.
Classification results by RBF-SVM model
RBF-SVM Goheung Whasun Shanxi Gansu Shaanxi Classification rate (%)
per group all groups
Training set (n=89) Goheung 35 0 0 0 0 100 96.6
Whasun 0 16 0 0 0 100
Shanxi 0 0 10 0 0 100
Gansu 0 0 0 17 0 100
Shaanxi 0 0 0 3 8 72.7
Test set (n=42) Goheung 17 0 0 0 0 100 85.7
Whasun 0 7 0 0 0 100
Shanxi 0 0 3 0 2 60
Gansu 0 0 0 7 1 87.5
Shaanxi 0 0 1 2 2 40

∗ The rows indicate the true sample class and that the columns refer to the observed class

TOOLS
Similar articles