This article has been
cited by other articles in ScienceCentral.
Abstract
This tutorial explains the basic principles of mechanistic ligand-receptor interaction model, which is an operational model of agonism. A growing number of agonist drugs, especially immune oncology drugs, is currently being developed. In this tutorial, time-dependent ordinary differential equation for simple Emax operational model of agonism was derived step by step. The differential equation could be applied in a pharmacodynamic modeling software, such as NONMEM, for use in non-steady state experiments, in which experimental data are generated while the interaction between ligand and receptor changes over time. Making the most of the non-steady state experimental data would simplify the experimental processes, and furthermore allow us to identify more detailed kinetics of a potential drug. The operational model of agonism could be useful to predict the optimal dose for agonistic drugs from in vitro and in vivo animal pharmacology experiments at the very early phase of drug development.
Keywords: Mechanistic ligand-receptor interaction, Operational model of agonism, Optimal dose, Prediction
Introduction
In 2006, six healthy volunteers in the UK who participated in a phase 1 study on TGN1412, a humanized CD28 agonist, had severe multiorgan failure.[
1] Because of this disaster, we recognized that a more appropriate approach to estimate the optimal initial dosing level is needed especially for drugs with agonistic mechanism.
The following is a scientific background about ligand receptor binding. Clark first introduced the drug-receptor binding concept in 1926 and his occupancy theory was elaborated during the mid of 20th century.[
2] Ligand-receptor binding kinetics is essential for the understanding of the drug. For example, the half-life of drug response could be independent of the pharmacokinetic half-life of the drug, if the dissociation rate constant (
Kdissoc) of the drug from the receptor is small, which means that the drug bound to receptor dissociates slowly. However, it is known that the relationship between percentage of occupied receptor by the drug and effect is not usually linear
in vivo, that is, the equilibrium dissociation rate constant (
KD) and
EC50 (drug concentration at the half-maximum effect) is different. To describe the discrepancies, an operational model of agonism was established by Black and Leff.[
3,
4] The unique characteristic of the operational model of agonism is the ‘transducer function’ which converts receptor occupation into pharmacological effect. Among all pharmacodynamics models, the
Emax model has the most robust theoretical base in ligand-receptor binding, according to the law of mass action.[
2] However, some drugs, such as the superagonist TGN1412, might exert its maximum effect at lower concentrations at which the receptors were not fully occupied.
In this tutorial, we mathematically derived operational model of agonism for simple ligand-receptor interaction model, which is essential for the understanding. Furthermore, we derived time-dependent ordinary differential equations for simple ligand-receptor interaction model, and operational model of agonism, which is potentially applicable in many in vitro and in vivo experiments to characterize and predict the response of a novel agonist at the very early stage of development.
Ligand-receptor interaction model
L and
R are ligand and receptor, respectively:
Assuming that the response is proportional to the ligand-receptor complex (LR), the amount or concentration of LR over time is our main interest.
The above equations can be rearranged as follows.
At equilibrium,
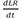
in the equation 2,
(

, equilibrium dissociation rate constant)
If
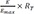
is substituted for
LR, with the assumption of
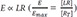
, differential equation for
E can be derived using equation 5 as follows.
The equation 7 can be applied to non-steady state experiments such as single dose pharmacokinetic and pharmacodynamic study in which the drug concentrations and responses were measured serially over time, as an example.
Where fLR is fraction of receptor occupied by drug.
Operational model of agonism
The operational model of agonism introduces transducer function that is stimulated by ligand-receptor complex (not ligand itself), which elicits the drug effect following the same way with the above equation 9, which can be described by the following equation 10 at this time.
Where Emax = maximal effect or response; E = effect elicited at a given level of occupancy, i.e., [LR]; KE = value of [LR] that elicits the half-maximal effect.
(Note that the L in equation 9 is replaced by LR in equation 10)
Substituting
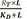
for
LR in the equation 10 (
LR =
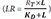
) can be obtained from the equation 8), the following equation is derived.
Assuming that receptor occupancy can be described by a rectangular hyperbolic expression, Black and Leff showed that the transducer function, the functions that links occupancy to response, must be hyperbolic if the observed
E/[L] relationship is hyperbolic.[
34] An important component used in this model is the transducer ratio, τ (tau)
The transducer ratio measures the efficiency of the transduction of receptor occupancy to biological effects. τ is affected by the properties of the tissue, concentration of receptors, and the consequences of drug-receptor interaction, or in other words, the potency of an agonist to elicit a response is affected by both receptor affinity to the agonist and receptor efficiency in translating receptor occupancy to response.
If RT>>KE (Spare receptor model), then
Since
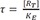
,
By substituting
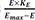
(LR =
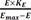
from equation 10) for
LR, from equation 5, a differential equation below is obtained.
The time-dependent differential equations derived in this tutorial would provide a framework for quantitative PK/PD modeling, which could be widely applied in pharmacological in vitro and non-clinical/clinical in vivo experiments for an agonist at non-steady state as well as steady state condition. This operational model of agonism could potentially provide critical information to predict optimal doses of agonists in various stages of clinical trials. For instance, it can potentially be used to obtain the most appropriate doses for future clinical trials including recommended starting dose for a first-in-human study, based on pharmacological in vitro and in vivo experiments at the early stage of drug development.
Acknowledgements
This study was supported by the Technology Innovation Program (grant numbers: 10067737, Establishment of risk management platform with aim to reduce attrition of new drugs and its service) funded by the Ministry of Trade, Industry & Energy (MI, Korea).
This study was also supported by a grant from the Korea Healthcare Technology R&D Project, Ministry for Health & Welfare, Republic of Korea (HI12C1847).
We thank Dr. Joon Seo Lim from the Scientific Publications Team at Asan Medical Center for his editorial assistance in preparing this manuscript.
References
1. Suntharalingam G, Perry MR, Ward S, Brett SJ, Castello-Cortes A, Brunner MD, et al. Cytokine storm in a phase 1 trial of the anti-CD28 monoclonal antibody TGN1412. N Engl J Med. 2006; 355:1018–1028. PMID:
16908486.

2. Salahudeen MS, Nishtala PS. An overview of pharmacodynamics modelling, ligand-binding approach and its application in clinical practice. Saudi Pharm J. 2017; 25:165–175. DOI:
10.1016/j.jsps.2016.07.002. PMID:
28344466.
3. Black JW, Leff P. Operational model of pharmacological agonism. Proc R Soc Lond B Biol Sci. 1983; 220:141–162. PMID:
6141562.
4. Black JW, Leff P, Shankley NP, Wood J. An operational model of pharmacological agonism: the effect of E/[A] curve shape on agonist dissociation constant estimation. Br J Pharmacol. 1985; 84:561–571. PMID:
3978322.

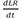 in the equation 2,
in the equation 2, , equilibrium dissociation rate constant)
, equilibrium dissociation rate constant)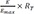 is substituted for LR, with the assumption of
is substituted for LR, with the assumption of 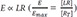 , differential equation for E can be derived using equation 5 as follows.
, differential equation for E can be derived using equation 5 as follows.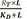 for LR in the equation 10 (LR =
for LR in the equation 10 (LR = 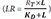 ) can be obtained from the equation 8), the following equation is derived.
) can be obtained from the equation 8), the following equation is derived.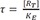 ,
,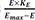 (LR =
(LR = 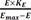 from equation 10) for LR, from equation 5, a differential equation below is obtained.
from equation 10) for LR, from equation 5, a differential equation below is obtained.



 PDF
PDF ePub
ePub Citation
Citation Print
Print


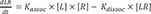
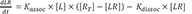
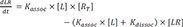
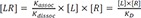
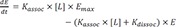
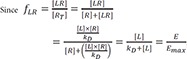
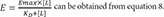
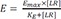
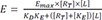
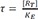
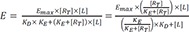
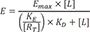
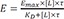
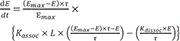
 XML Download
XML Download