PDF
ePub
Citation
Print
Abstract
Purpose
The effect of global inhomogeneity on quantitative susceptibility mapping (QSM) was investigated. A technique referred to as Simultaneous Unwrapping Phase with Error Recovery from inhomogeneity (SUPER) is suggested as a preprocessing to QSM to remove global field inhomogeneity-induced phase by polynomial fitting.
Materials and Methods
The effect of global inhomogeneity on QSM was investigated by numerical simulations. Three types of global inhomogeneity were added to the tissue susceptibility phase, and the root mean square error (RMSE) in the susceptibility map was evaluated. In-vivo QSM imaging with volunteers was carried out for 3.0T and 7.0T MRI systems to demonstrate the efficacy of the proposed method.
Results
The SUPER technique removed harmonic and non-harmonic global phases. Previously only the harmonic phase was removed by the background phase removal method. The global phase contained a non-harmonic phase due to various experimental and physiological causes, which degraded a susceptibility map. The RMSE in the susceptibility map increased under the influence of global inhomogeneity; while the error was consistent, irrespective of the global inhomogeneity, if the inhomogeneity was corrected by the SUPER technique. In-vivo QSM imaging with volunteers at 3.0T and 7.0T MRI systems showed better definition in small vascular structures and reduced fluctuation and non-uniformity in the frontal lobes, where field inhomogeneity was more severe.
Conclusion
Correcting global inhomogeneity using the SUPER technique is an effective way to obtain an accurate susceptibility map on QSM method. Since the susceptibility variations are small quantities in the brain tissue, correction of the inhomogeneity is an essential element for obtaining an accurate QSM.
References
1. Salomir R, de Senneville BD, Moonen CT. A fast calculation method for magnetic field inhomogeneity due to an arbitrary distribution of bulk susceptibility. Concepts in Magn Reson Part B (Magn Reson Engineering). 2003; 19B:26–34.
2. Cho ZH. Review of recent advancement of ultra high field magnetic resonance imaging: from anatomy to tractography. Investig Magn Reson Imaging. 2016; 20:141–151.
3. Haacke EM, Xu Y, Cheng YC, Reichenbach JR. Susceptibility weighted imaging (SWI). Magn Reson Med. 2004; 52:612–618.
4. Sehgal V, Delproposto Z, Haacke EM, et al. Clinical applications of neuroimaging with susceptibility-weighted imaging. J Magn Reson Imaging. 2005; 22:439–450.
5. Mittal S, Wu Z, Neelavalli J, Haacke EM. Susceptibility-weighted imaging: technical aspects and clinical applications, part 2. AJNR Am J Neuroradiol. 2009; 30:232.
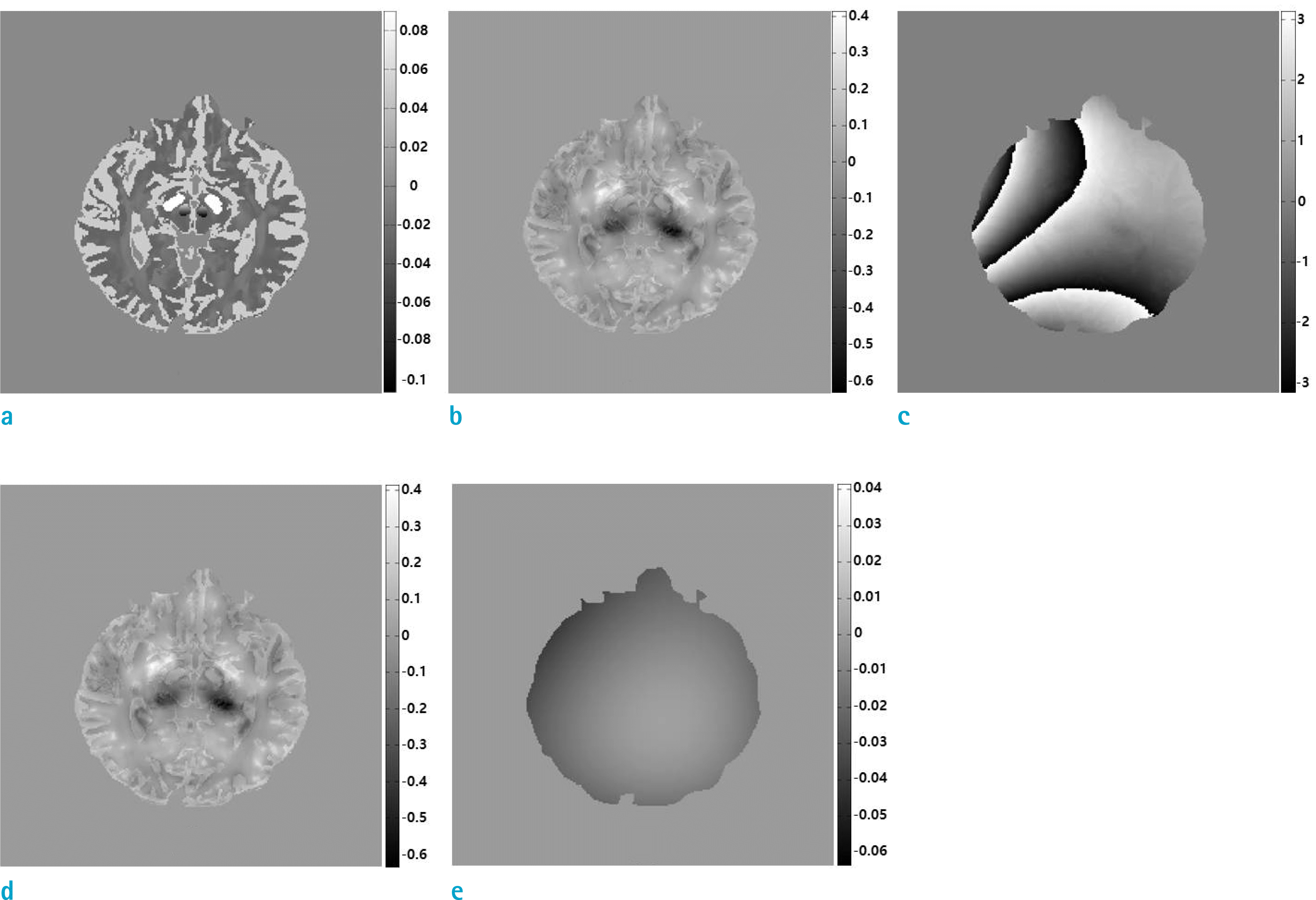Fig. 1.
Numerical phantom for the simulation: (a) An axial plane of the susceptibility data, (b) corresponding tissue phase, (c) combined phase with the global inhomogeneity-induced phase, (d) remaining phase after the global phase removal by SUPER, and (e) the difference between (b) and (d).
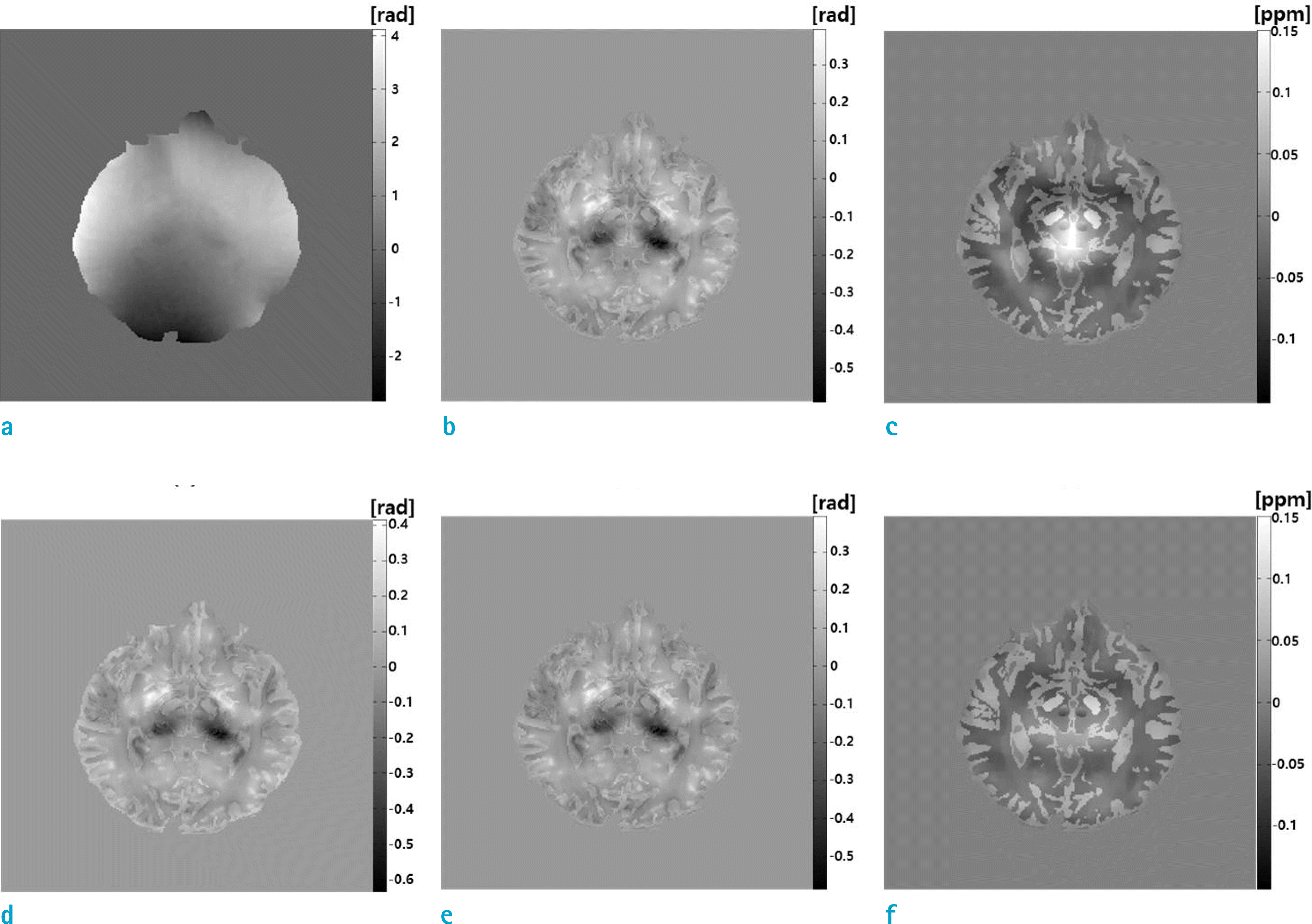Fig. 2.
The QSM without, and with the global inhomogeneity correction are shown in the upper and lower rows, respectively: (a) unwrapped phase by the Laplacian unwrapping, (b) phase after removal of the background susceptibility-induced phase by SHARP, and (c) susceptibility map; and (d) phase after SUPER, (e) phase after SHARP, and (f) susceptibility map.
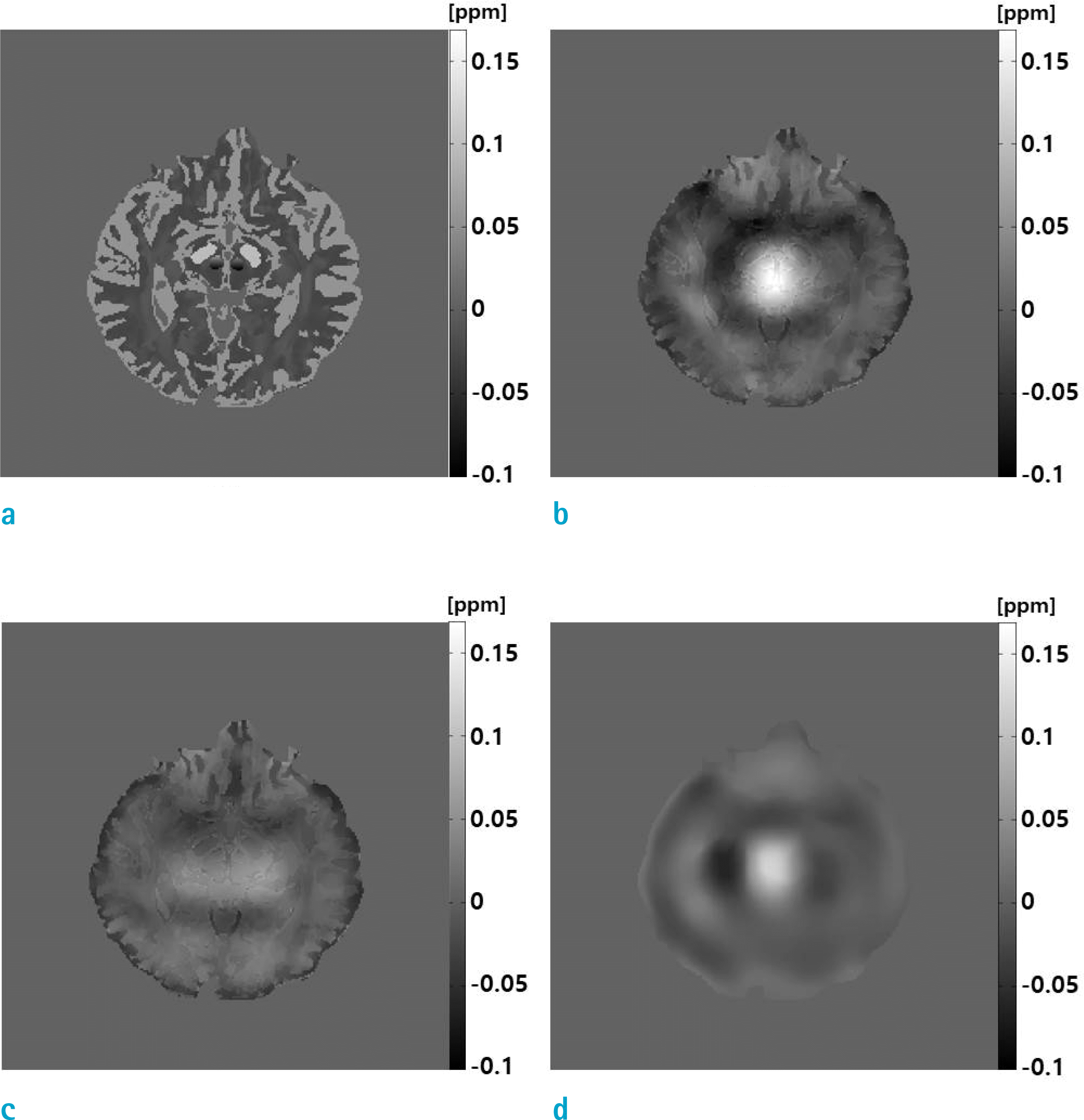Fig. 3.
Errors of the susceptibility map are shown: (a) True susceptibility map, (b) error of the map without global inhomogeneity correction, (c) error of the map with the global inhomogeneity correction, and (d) susceptibility map from the global inhomogeneity-induced phase. Note the similarity between (b) and (d), which ensures that the error is due to the global inhomogeneity.
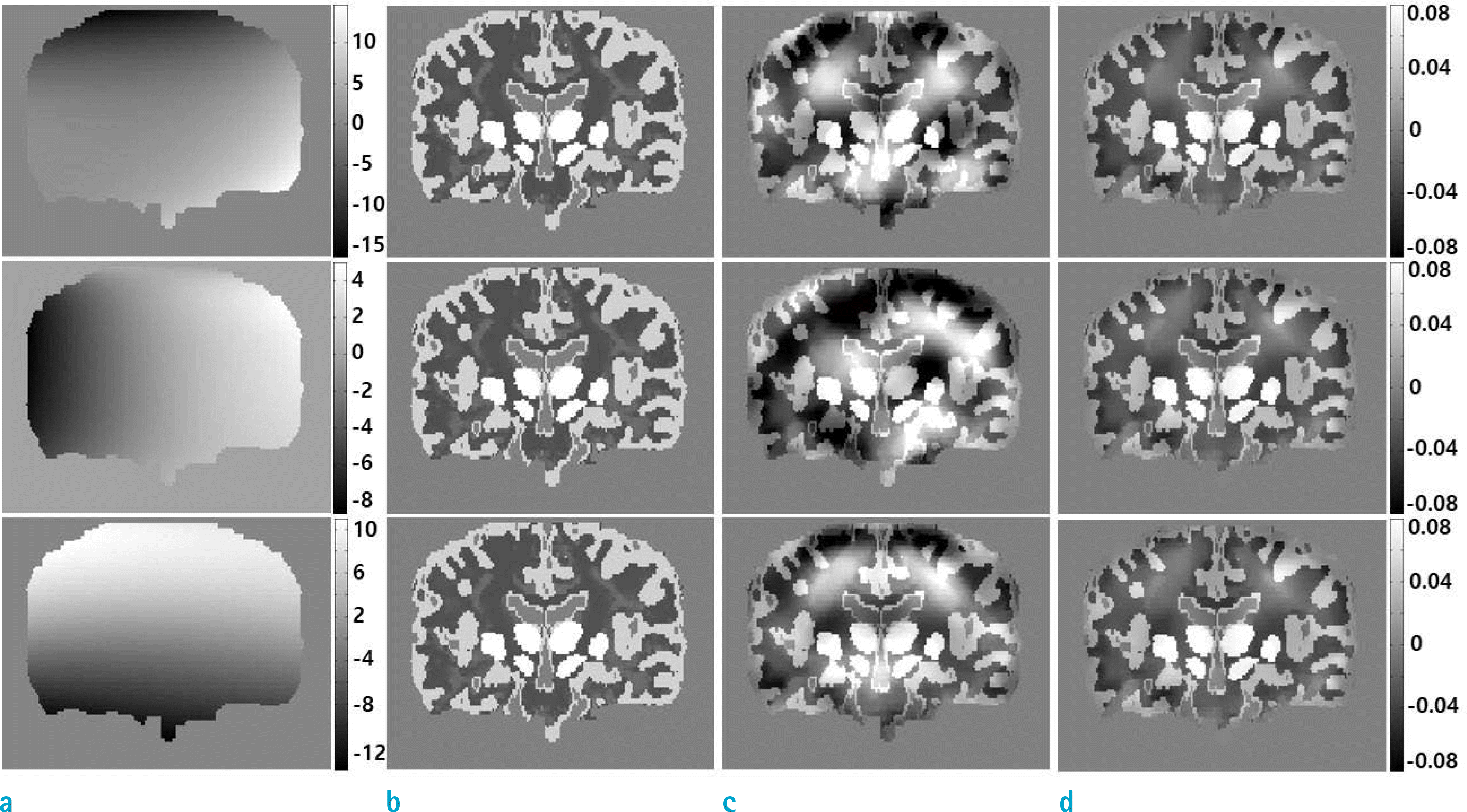Fig. 4.
Susceptibility maps are shown under the three inhomogeneity types: (a) global inhomogeneity phase, (b) true susceptibility maps, (c) susceptibility maps obtained without global inhomogeneity correction, and (d) susceptibility maps obtained with the global inhomogeneity correction by SUPER. The global inhomogeneity is modeled from a 3.0T MRI, a 7.0T MRI, and a non-physical model, from top to bottom.
Fig. 5.
In vivo QSM imaging at 3.0T MRI. Axial, sagittal, and coronal planes are shown from top to bottom: (a) Magnitude images, (b) wrapped phase images, (c) estimated global inhomogeneity by SUPER, (d) and (e) tissue susceptibility-induced phases without and with the global inhomogeneity correction, respectively, (f) difference, (g) and (h) susceptibility maps without and with the global inhomogeneity correction, respectively, and (i) difference. Distinctly different regions in the susceptibility maps are marked with small arrows.
Fig. 6.
In vivo QSM imaging for 7.0T MRI. Axial, sagittal, and coronal planes are shown from top to bottom: (a) magnitudes, (b) wrapped phases, (c) estimated inhomogeneity by SUPER, (d) and (g) tissue susceptibility-induced phase and the susceptibility map without global inhomogeneity correction, (e) and (h) tissue phase and susceptibility map with the global inhomogeneity correction, and (f) and (i) differences between the two phases and the susceptibility maps, respectively. Regions of distinct differences in the susceptibility maps are marked with small arrows.
Table 1.
RMSE of Susceptibility Map in PPM without and with Global Inhomogeneity Correction, RMSE for Unwrapped Phase in Parenthesis
XML Download