PDF
ePub
Citation
Print
Abstract
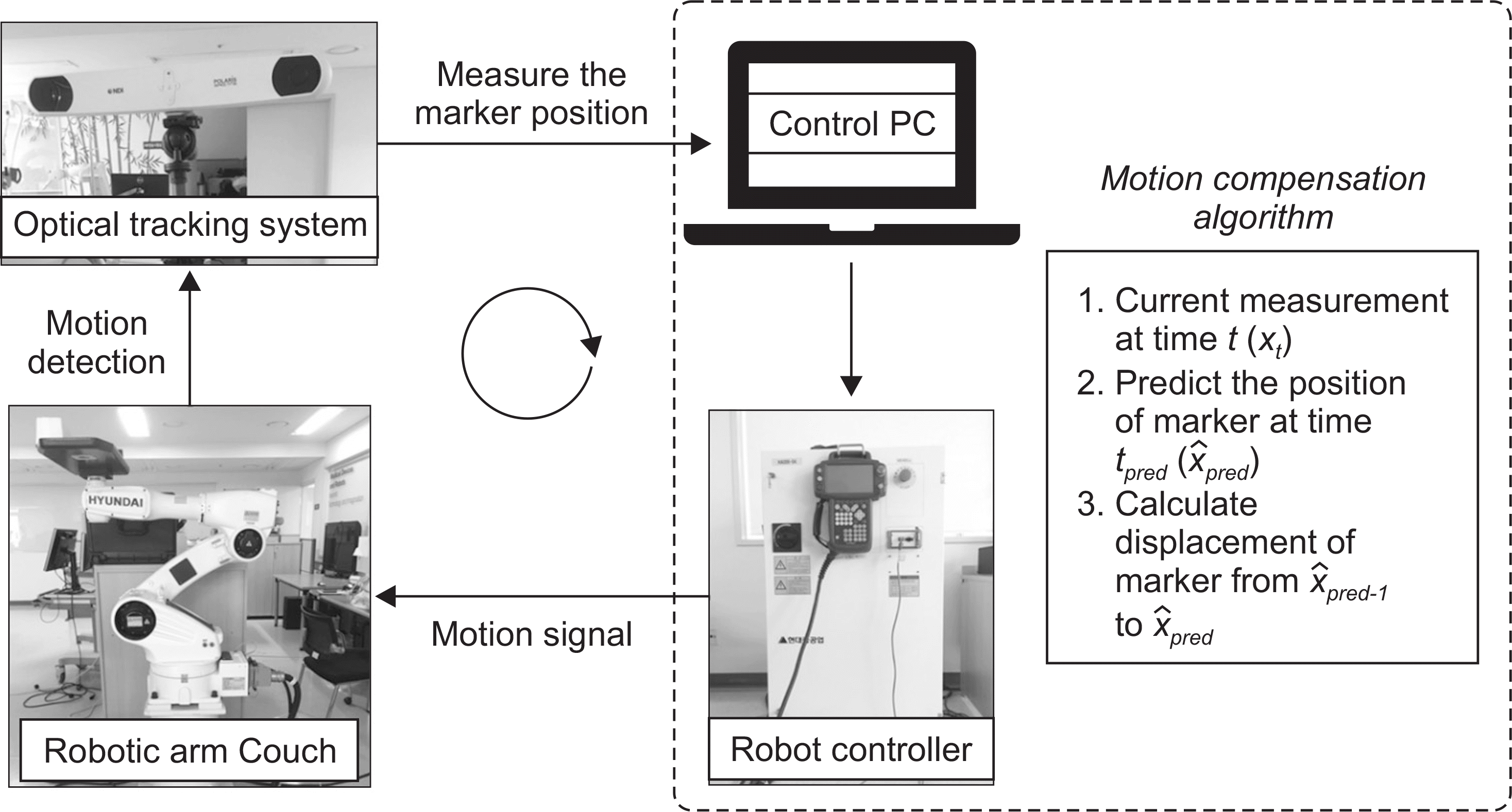
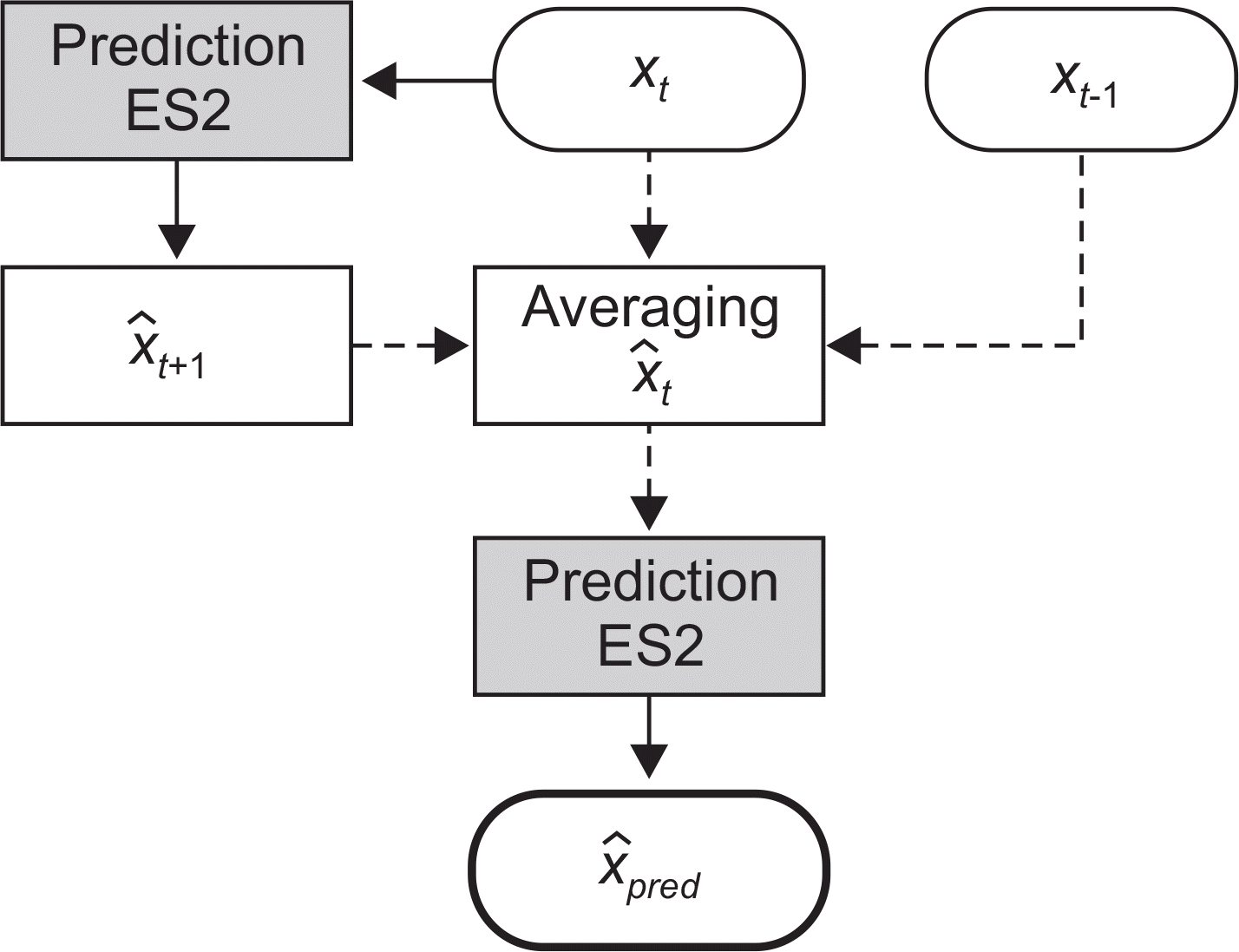
The purpose of this study is to install a system that compensated for the respiration motion using an articulated robotic manipulator couch which enables a wide range of motions that a Stewart platform cannot provide and to evaluate the performance of various prediction algorithms including proposed algorithm. For that purpose, we built a miniature couch tracking system comprising an articulated robotic manipulator, 3D optical tracking system, a phantom that mimicked respiratory motion, and control software. We performed simulations and experiments using respiratory data of 12 patients to investigate the feasibility of the system and various prediction algorithms, namely linear extrapolation (LE) and double exponential smoothing (ES2) with averaging methods. We confirmed that prediction algorithms worked well during simulation and experiment, with the ES2-averaging algorithm showing the best results. The simulation study showed 43% average and 49% maximum improvement ratios with the ES2-averaging algorithm, and the experimental study with the QUASARTM phantom showed 51% average and 56% maximum improvement ratios with this algorithm. Our results suggest that the articulated robotic manipulator couch system with the ES2-averaging prediction algorithm can be widely used in the field of radiation therapy, providing a highly efficient and utilizable technology that can enhance the therapeutic effect and improve safety through a noninvasive approach.
REFERENCES
1.Keall PJ., Mageras GS., Balter JM, et al. The management of respiratory motion in radiation oncology report of AAPM Task Group 76. Med. Phys. 2006. 33(10):3874–900.
2.Chung H., Cho S., Cho B. Feasibility Study of Robotics-based Patient Immobilization Device for Real-time Motion Compensation. Prog Med Phys. 2016. 27(3):117–24.
3.Depuydt T., Verellen D., Haas O, et al. Geometric accuracy of a novel gimbals based radiation therapy tumor tracking system. Radiother Oncol. 2011. 98(3):365–72.
4.Engelsman M., Sharp GC., Bortfeld T, et al. How much margin reduction is possible through gating or breath hold? Phys. Med. Biol. 2005. 50(3):477–90.
5.Stevens CW., Munden RF., Forster KM, et al. Respiratory-driven lung tumor motion is independent of tumor size, tumor location, and pulmonary function. Int. J. Radiation Oncology Biol. Phys. 2001. 51(1):62–8.
6.Sharp GC., Jiang SB., Shimizu S., Shirato H. Prediction of respiratory tumour motion for real-time image-guided radiotherapy. Phys. Med. Biol. 2004. 49(3):425–40.
7.Murphy MJ. Tracking moving organs in real time. Semin Radiat Oncol. 2004. 14(1):91–100.
8.Putra D., Haas OCL., Mills JA., Burnham KJ. A multiple model approach to respiratory motion prediction for realtime IGRT. Phys. Med. Biol. 2008. 53(6):1651–63.
9.Murphy MJ., Pokhrel D. Optimization of an adaptive neural network to predict breathing. Med. Phys. 2009. 36(1):40–7.
10.Kalet A., Sandison G., Wu H., Schmitz R. A state-based probabilistic model for tumor respiratory motion prediction. Phys. Med. Biol. 2010. 55(24):7615–31.
11.Ren Q., Nishioka S., Shirato H., Berbeco RI. Adaptive prediction of respiratory motion for motion compensation radiotherapy. Phys. Med. Biol. 2007. 52(22):6651–61.
12.Ernst F., Schweikard A. Predicting respiratory motion signals for image-guided radiotherapy using multi-step linear methods (MULIN). Int J Comput Assist Radiol Surg. 2008. 3(1):85–90.
13.Ernst F., Schlaefer A., Schweikard A. Prediction of Respiratory Motion with Wavelet-Based Multiscale Autoregression. Proc. of the 10th int. conf. on Medical image computing and computer-assisted intervention, MICCAI (Berlin, Germany). 2007. 668–75.
14.Chiesa S., Placidi L., Azario L, et al. Adaptive optimization by 6 DOF robotic couch in prostate volumetric IMRT treatment: rototranslational shift and dosimetric consequences. J Appl Clin Med Phys. 2015. 16(5):35–45.
15.D'Souza WD., Naqvi SA., Yu CX. Real-time intra-fraction-motion tracking using the treatment couch: a feasibility study. Phys. Med. Biol. 2005. 50:4021–33.
16.Kilby W., Dooley JR., Kuduvalli G, et al. The CyberKnife Robotic Radiosurgery System in 2010. Technol. Cancer Res. Treat. 2010. 9(5):433–52.
17.Diebel J. Representing Attitude: Euler Angles, Unit Quaternions, and Rotation Vectors. Matrix. 2006. 58:1–35.
18.Krilavicius T., Zliobaite I., Simonavicius H., Jarusevicius L. Predicting respiratory motion for real-time tumour tracking in radiotherapy. 2016 IEEE 29th International Symposium on Computer-Based Medical Systems (CBMS), (Dublin, Ireland). 2016. 1–33.
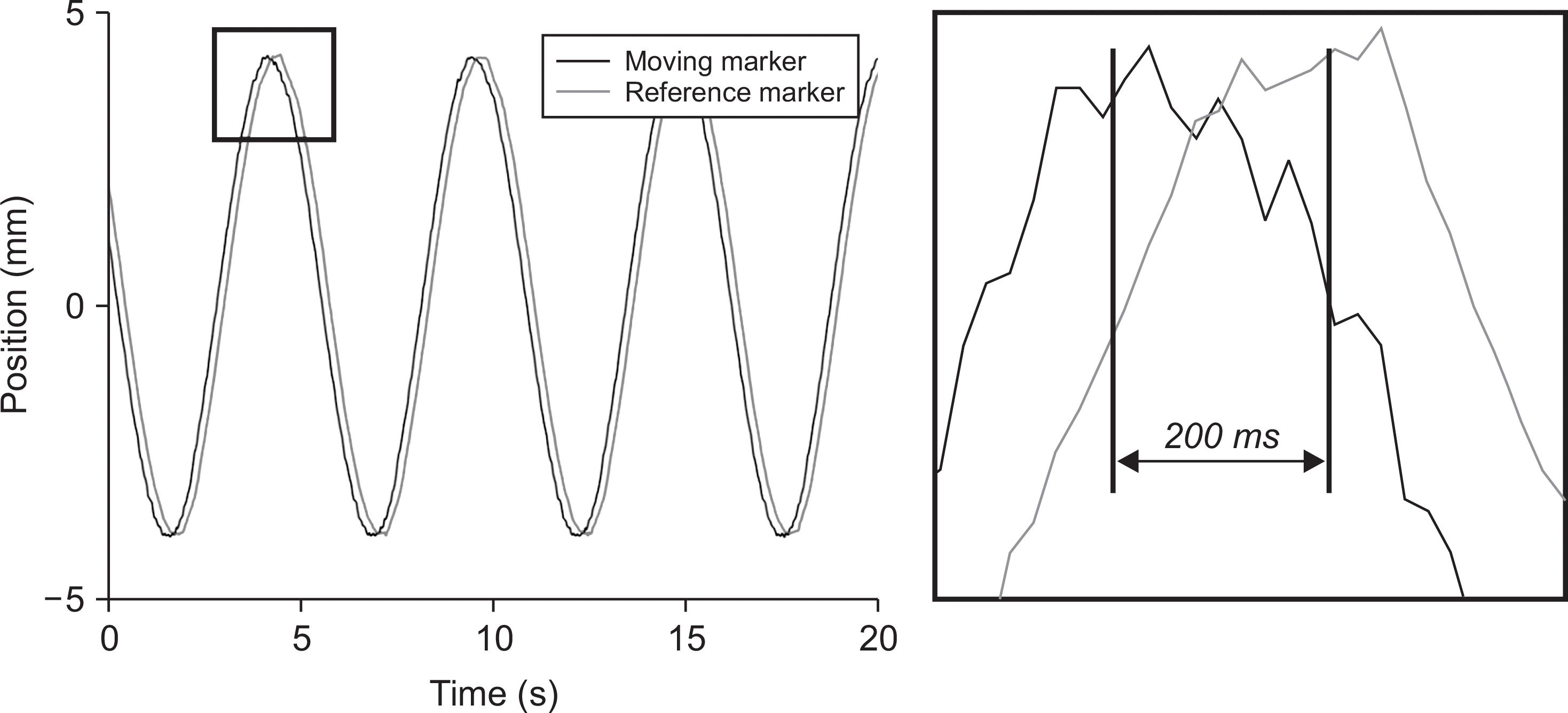Fig. 3
Marker displacement on the rotation phantom and couch, obtained using the tracking system without applying a prediction algorithm. The inset shows a segment of the same signal.
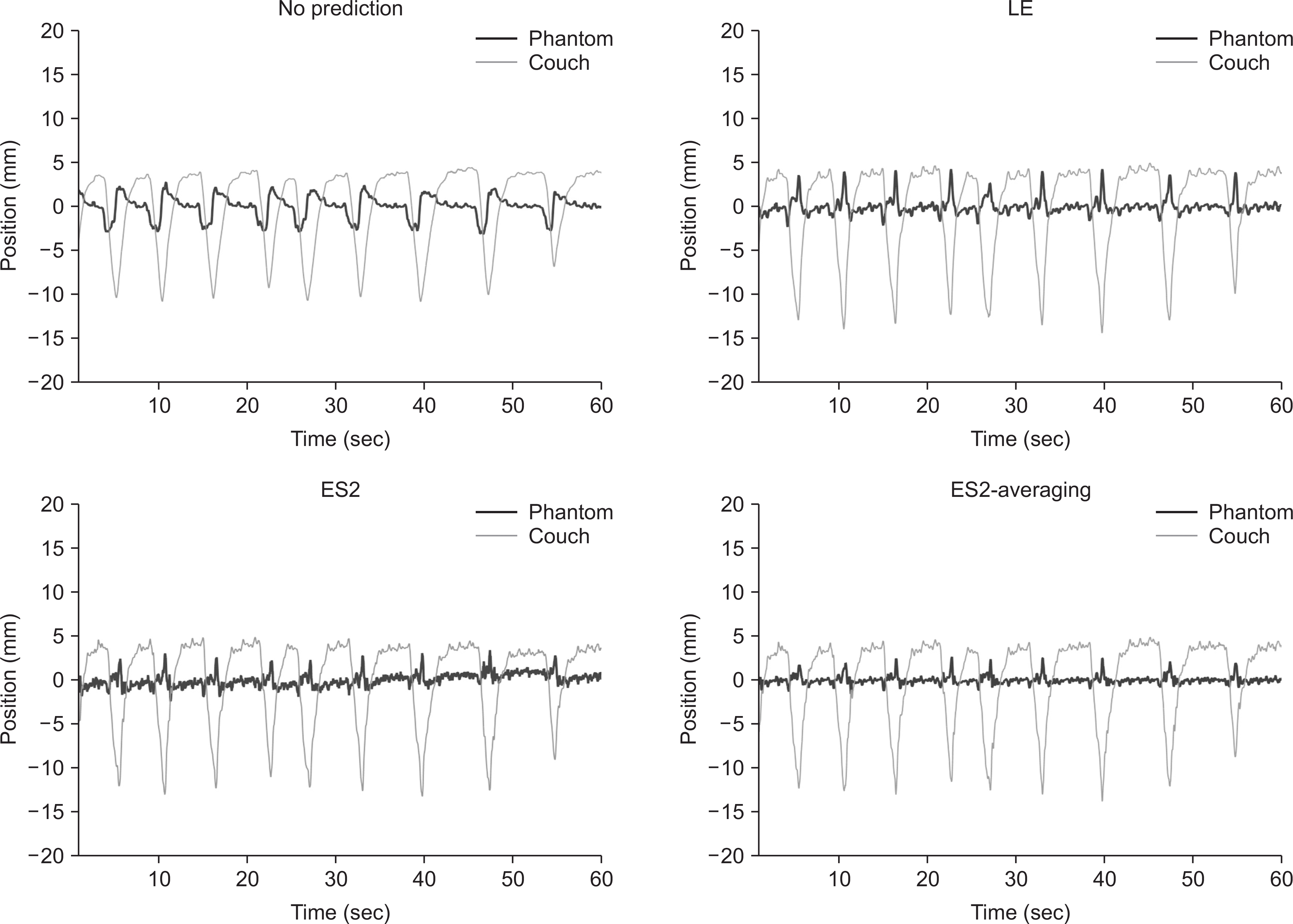Fig. 5
Marker displacements for one (patient 5) out of 12 patients when applying the various prediction algorithms in the experimental study. The thick line indicates the phantom motion; ideally, this should appear still, indicating no relative movement between the phantom and couch.
Table 1.
Three-dimensional RMSE values and improvement ratios in the simulation study
Table 2.
Three-dimensional RMSE values and improvement ratios for the experimental study using the QUASARTM phantom
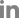
XML Download