PDF
ePub
Citation
Print
Abstract
The difference between three-dimensional (3D) and four-dimensional (4D) dose could be affected by factors such as tumor size and motion. To quantitatively analyze the effects of these factors, a phantom that can independently control each factor is required. The purpose of this study is to develop a deformable lung phantom with the above attributes and evaluate the characteristics. A phantom was designed to simulate diaphragm motion with amplitude in the range 1~7 cm and period up to ≥2 s of regular breathing. To simulate different tumors sizes, custom molds were created using a 3D printer and filled with liquid silicone. The accuracy of the phantom diaphragm motion was assessed by comparing measured motion with predicted motion. Because the phantom diaphragm motion is not identical to the tumor motion, the correlation between the diaphragm and tumor motions was calculated by a curve fitting method to emulate user-intended tumor motion. Tumors of different sizes were located at same position, and tumor setup positions were evaluated. The accuracy of phantom diaphragm motion was better than 1 mm. The diaphragm-tumor correlation showed that the tumor motion in the superior-inferior direction increased with increasing diaphragm motion. The tumor motion was larger in the 10 cm3 tumor than in the 90 cm3 tumor. The range of difference between the tumor setup positions was 0 to 0.45 cm. This phantom showed independently adjusting factors such as tumor size and motion to facilitate quantitative analysis of the dosimetric impact of respiratory motion according to these factors.
REFERENCES
1. Low DA, Nystrom M, Kalinin E, Parikh P, Dempsey JF, Bradley JD, et al. A method for the reconstruction of four-dimensional synchronized CT scans acquired during free breathing. Med Phys. 2003; 30:1254–1263.
2. Pan T, Lee T-Y, Rietzel E, Chen GTY. 4D-CT imaging of a volume influenced by respiratory motion on multislice CT. Med Phys. 2004; 31:333–340.
3. Keall P. 4-dimensional computed tomography imaging and treatment planning. Semin Radiat Oncol. 2004; 14:81–90.
4. Bortfeld T, Jiang SB, Rietzel E. Effects of motion on the total dose distribution. Semin Radiat Oncol. 2004; 14:41–51.
5. Brock KK, McShan DL, Ten Haken RK, Hollister SJ, Dawson LA, Balter JM. Inclusion of organ deformation in dose calculations. Med Phys. 2003; 30:290–295.
6. Jung SH, Yoon SM, Park SH, Cho B, Park JW, Jung J, et al. Four-dimensional dose evaluation using deformable image registration in radiotherapy for liver cancer. Med Phys. 2013; 40:011706.
7. Starkschall G, Britton K, McAleer MF, Jeter MD, Kaus MR, Bzdusek K, et al. Potential dosimetric benefits of four-dimensional radiation treatment planning. Int J Radiat Oncol Biol Phys. 2009; 73:1560–1565.
8. Valdes G, Robinson C, Lee P, Morel D, Low D, Iwamoto KS, et al. Tumor control probability and the utility of 4D vs 3D dose calculations for stereotactic body radiotherapy for lung cancer. Med Dosim. 2015; 40:64–69.
9. Werner R, Ehrhardt J, Schmidt-Richberg A, Albers D, Frenzel T, Petersen C, et al. Towards accurate dose accumulation for Step-&-Shoot IMRT: Impact of weighting schemes and temporal image resolution on the estimation of dosimetric motion effects. Z Med Phys. 2012; 22:109–122.
10. Guckenberger M, Wilbert J, Krieger T, Richter A, Baier K, Meyer J, et al. Four-Dimensional Treatment Planning for Stereotactic Body Radiotherapy. Int J Radiat Oncol Bio Phys. 2007; 69:276–285.
11. Admiraal MA, Schuring D, Hurkmans CW. Dose calculations accounting for breathing motion in stereotactic lung radiotherapy based on 4D-CT and the internal target volume. Radiother Oncol. 2008; 86:55–60.
12. Yeo UA, Taylor ML, Supple JR, Siva S, Kron T, Pham D, et al. Evaluation of dosimetric misrepresentations from 3D conventional planning of liver SBRT using 4D deformable dose integration. J Appl Clin Med Phys. 2014; 15:188–203.
13. Starkschall G, Gibbons JP, Orton CG. To ensure that target volumes are not underirradiated when respiratory motion may affect the dose distribution, 4D dose calculations should be performed. Med Phys. 2009; 36:1–3.
14. Chang J, Suh T-S, Lee D-S. Development of a deformable lung phantom for the evaluation of deformable registration. J Appl Clin Med Phys. 2010; 11:281–286.
15. Serban M, Heath E, Stroian G, Collins DL, Seuntjens J. A deformable phantom for 4D radiotherapy verification: Design and image registration evaluation. Med Phys. 2008; 35:1094–1102.
16. Belyaev O, Herden H, Meier JJ, Muller CA, Seelig MH, Herzog T, et al. Assessment of Pancreatic Hardness—Surgeon versus Durometer. J Surg Res. 2010; 158:53–60.
17. Kashani R, Lam K, Litzenberg D, Balter J. Technical note: A deformable phantom for dynamic modeling in radiation therapy. Med Phys. 2007; 34:199–201.
18. Liu HH, Balter P, Tutt T, Choi B, Zhang J, Wang C, et al. Assessing RespirationInduced Tumor Motion and Internal Target Volume Using Four-Dimensional Computed Tomography for Radiotherapy of Lung Cancer. Int J Radiat Oncol Bio Phys. 2007; 68:531–540.
19. Li F, Li J, Zhang Y, Shang D, Fan T, Liu T, et al. Geometrical differences in gross target volumes between 3DCT and 4DCT imaging in radiotherapy for non-small-cell lung cancer. J Radiat Res. 2013; 54:950–956.
20. Mageras GS, Pevsner A, Yorke ED, Rosenzweig KE, Ford EC, Hertanto A, et al. Measurement of lung tumor motion using respiration-correlated CT. Int J Radiat Oncol Bio Phys. 2004; 60:933–941.
21. Elena N, Symonds-Tayler JRN, James LB, Steve W. Quantifying the effect of respiratory motion on lung tumour dosimetry with the aid of a breathing phantom with deforming lungs. Phys Med Biol. 2006; 51:3359–3374.
22. Sarker J, Chu A, Mui K, Wolfgang JA, Hirsch AE, Chen GTY, et al. Variations in tumor size and position due to irregular breathing in 4D-CT: A simulation study. Med Phys. 2010; 37:1254–1260.
23. Aznar MC, Persson GF, Kofoed IM, Nygaard DE, Korreman SS. Irregular breathing during 4DCT scanning of lung cancer patients: Is the midventilation approach robust? Phys Medica. 2014; 30:69–75.
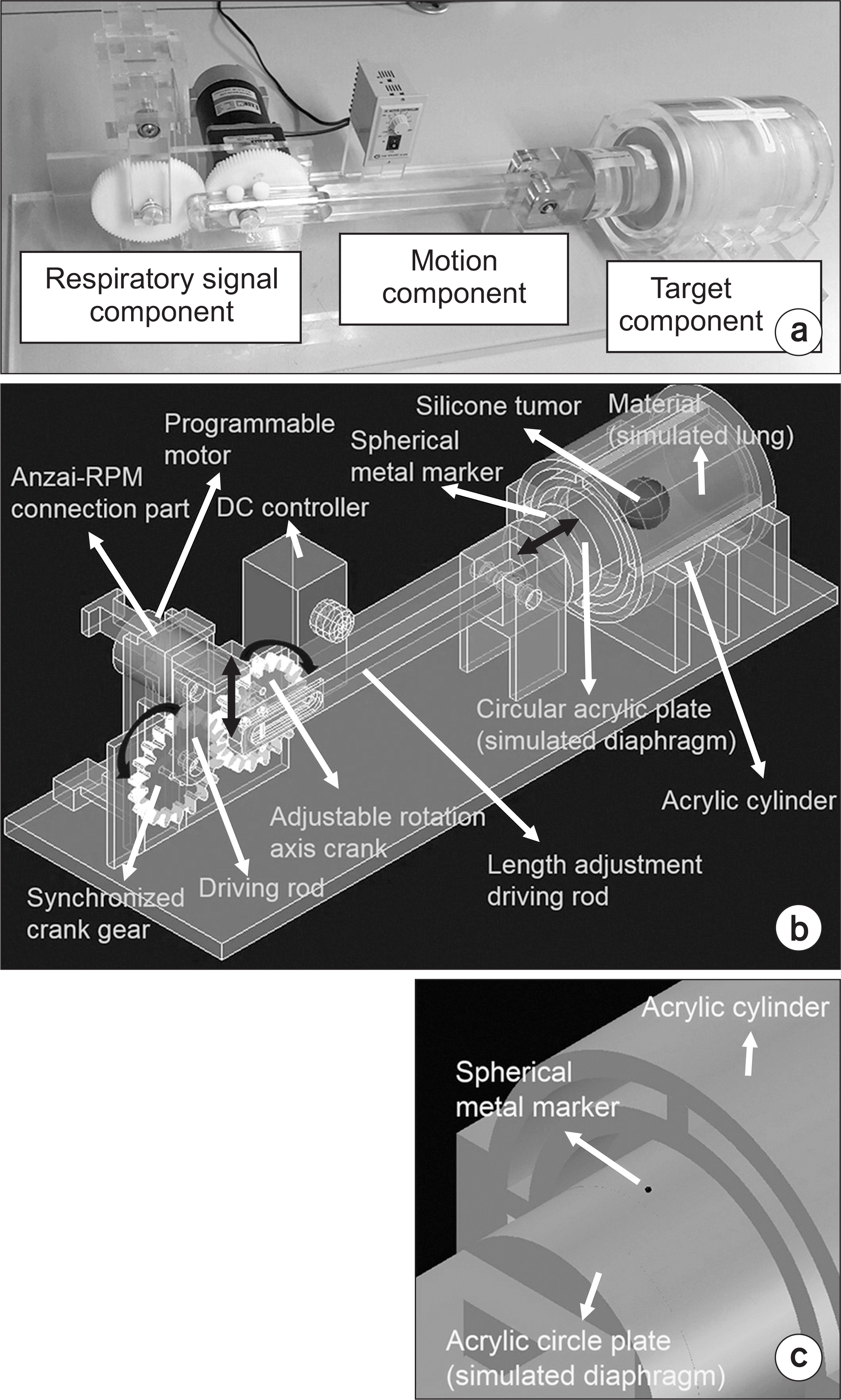Fig. 1.
Developed deformable lung phantom comprising target, motion, and respiratory signal components. The blue arrows describe the phantom motions. (a) Photograph, (b) overall diagram in AutoCAD (Auto CAD 2016, Autodesk Inc, San Rafael, CA), and (c) enlarged image of the upper side of the acrylic circle plate.
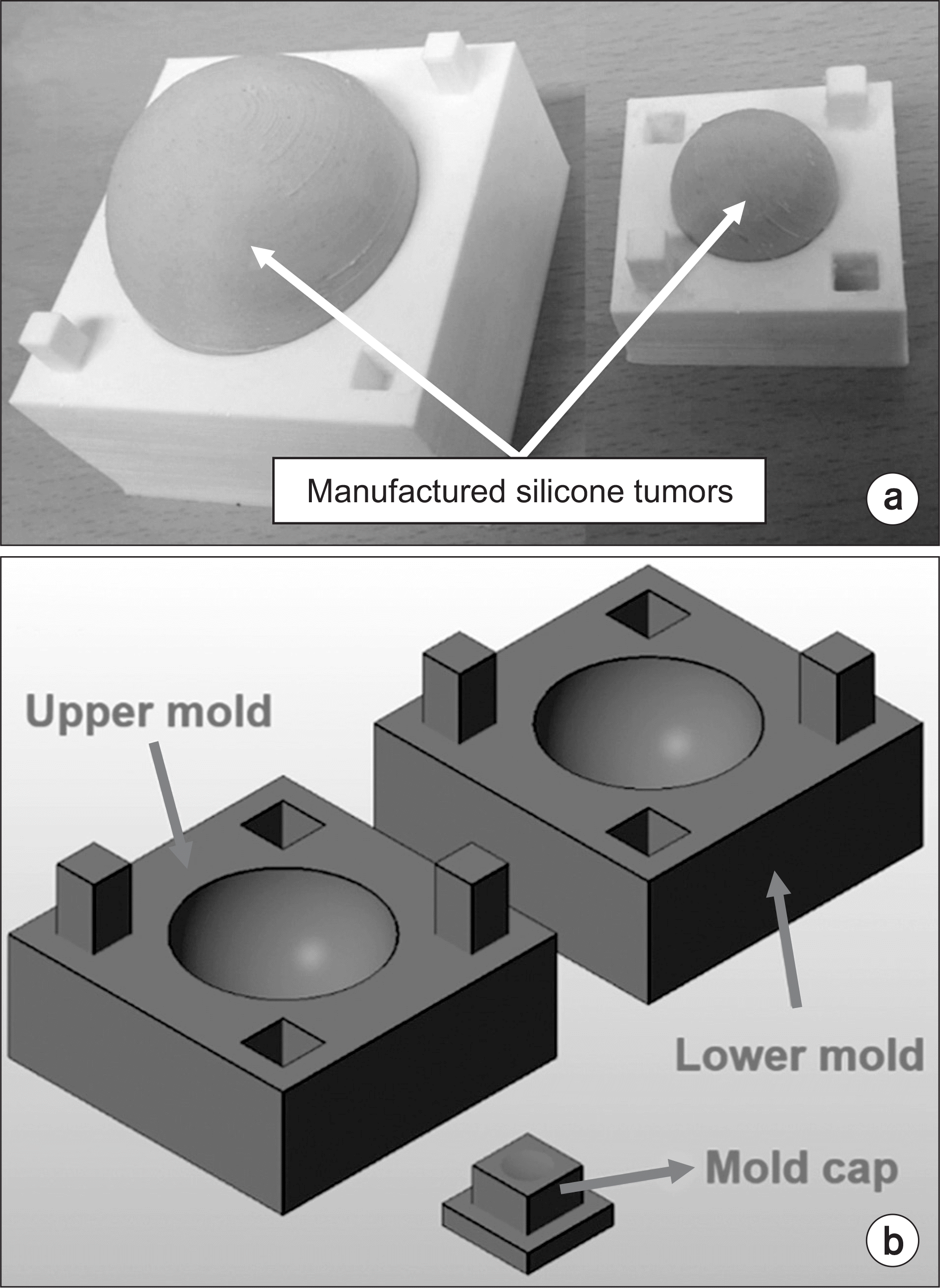Fig. 2.
Tumor molds manufactured using a three-dimensional (3D) printer. Tumors of different sizes were produced using liquid silicone rubber and molds. (a) Photograph of tumors in the tumor molds that have 90 cm3 and 10 cm3 tumor sizes, respectively, and (b) diagram of the tumor mold set for a 3D printing.
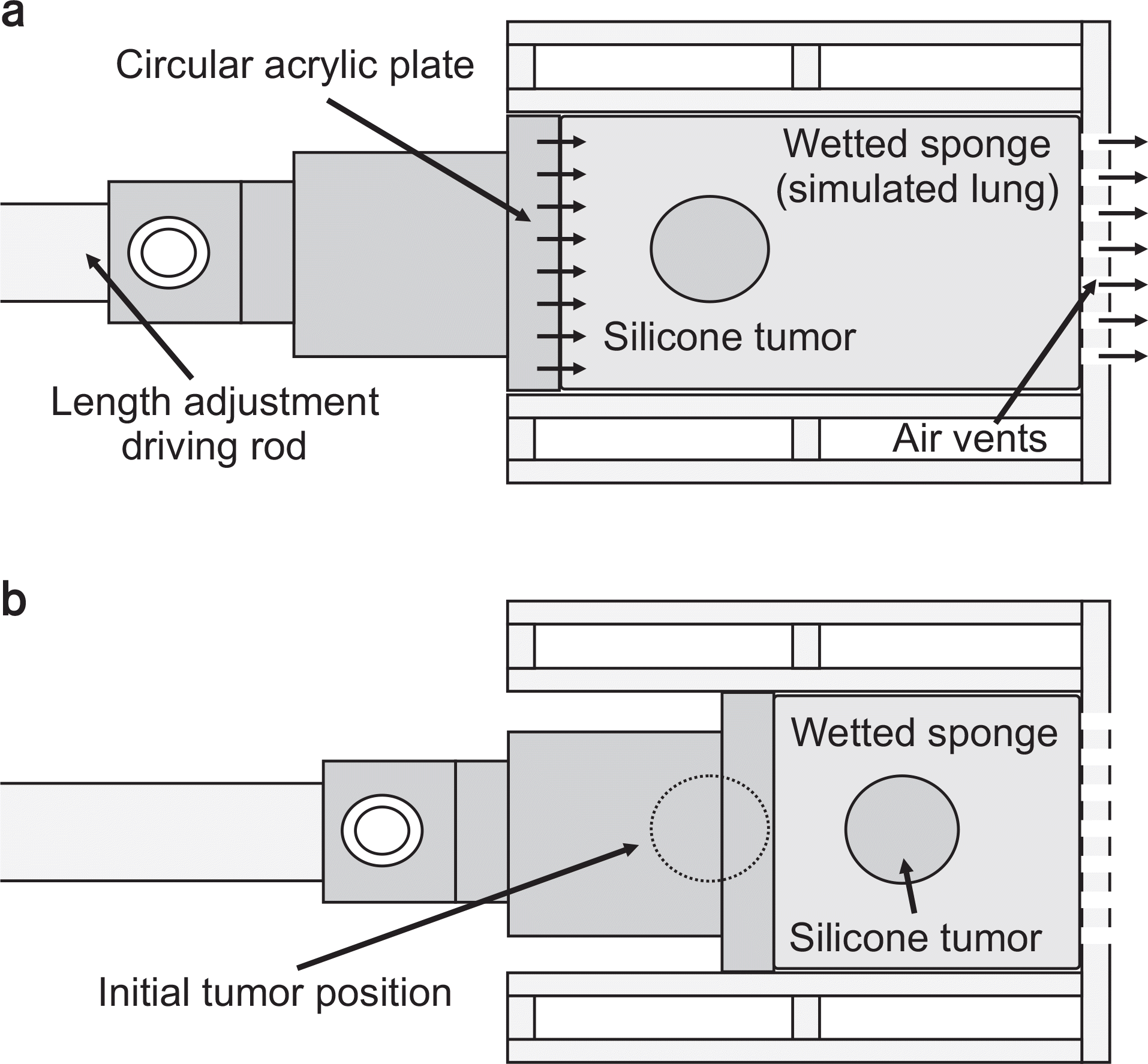Fig. 3.
Detailed motion of the phantom in the target component. (a) End-inhalation phase, and (b) end-exhalation phase.
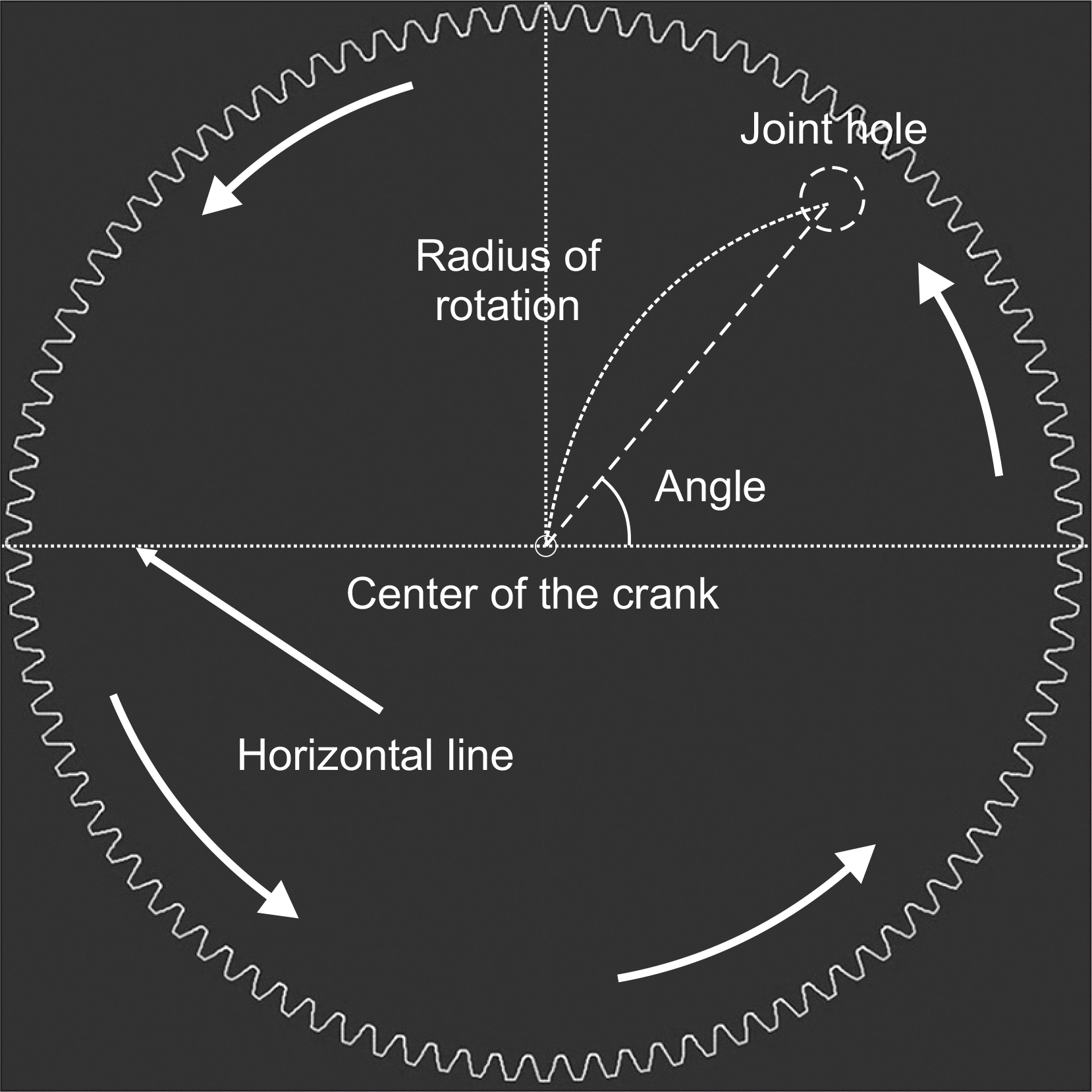Fig. 4.
Detailed two-dimensional diagram of the adjustable rotation axis crank. The horizontal line (red dotted line) is parallel with the bottom surface of the phantom. The joint hole is the connection point between the length adjustment driving rod and the adjustable rotation axis crank, and the angle is defined on the basis of the horizontal line and a line (white dashed line) from the crank center to the joint hole. The radius of rotation is the distance between the center of the crank to the joint hole. The red arrows describe the crank motion.
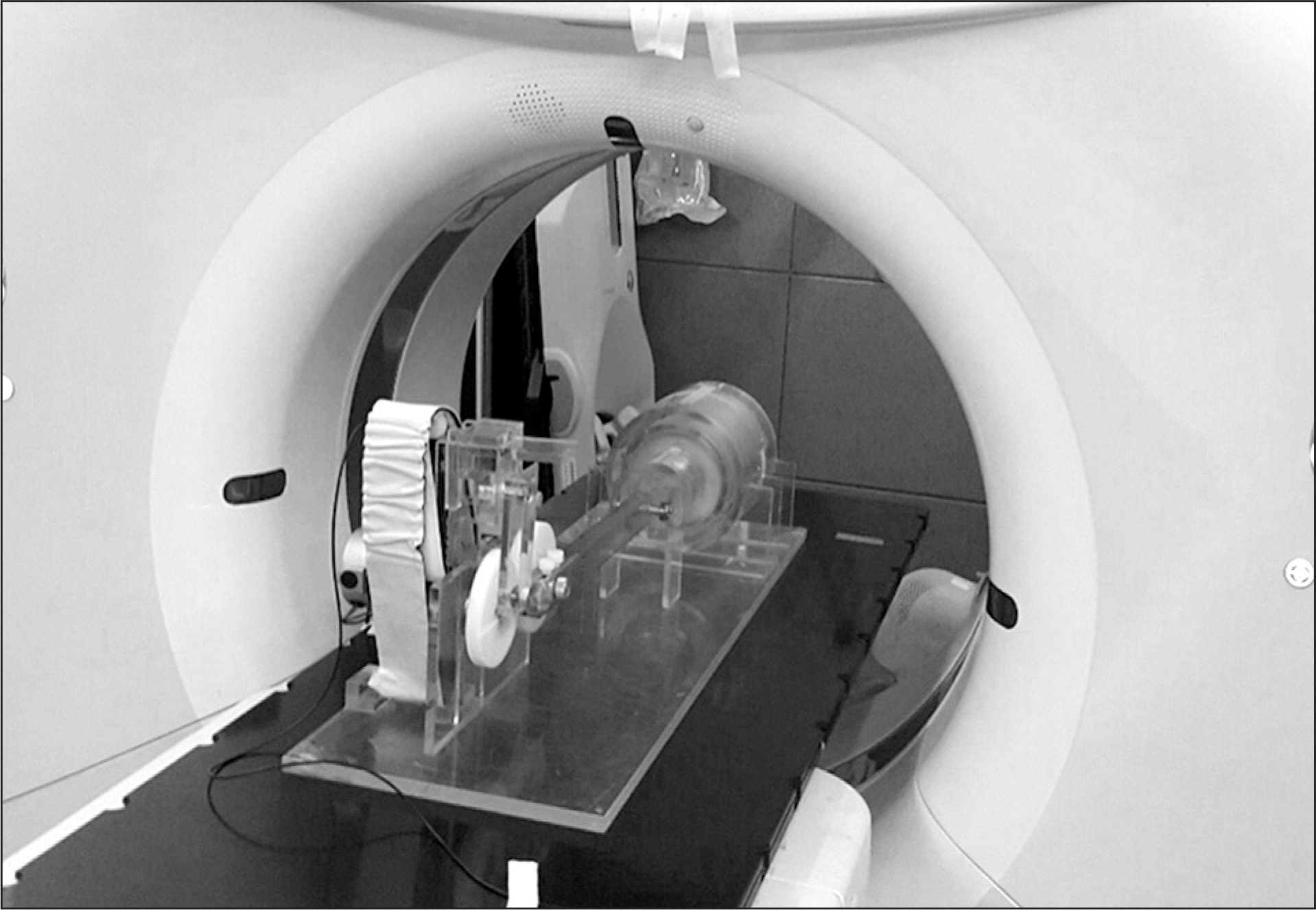Fig. 5.
The setup of the developed phantom equipped with the ANZAI belt to acquire four-dimensional computed tomography data.
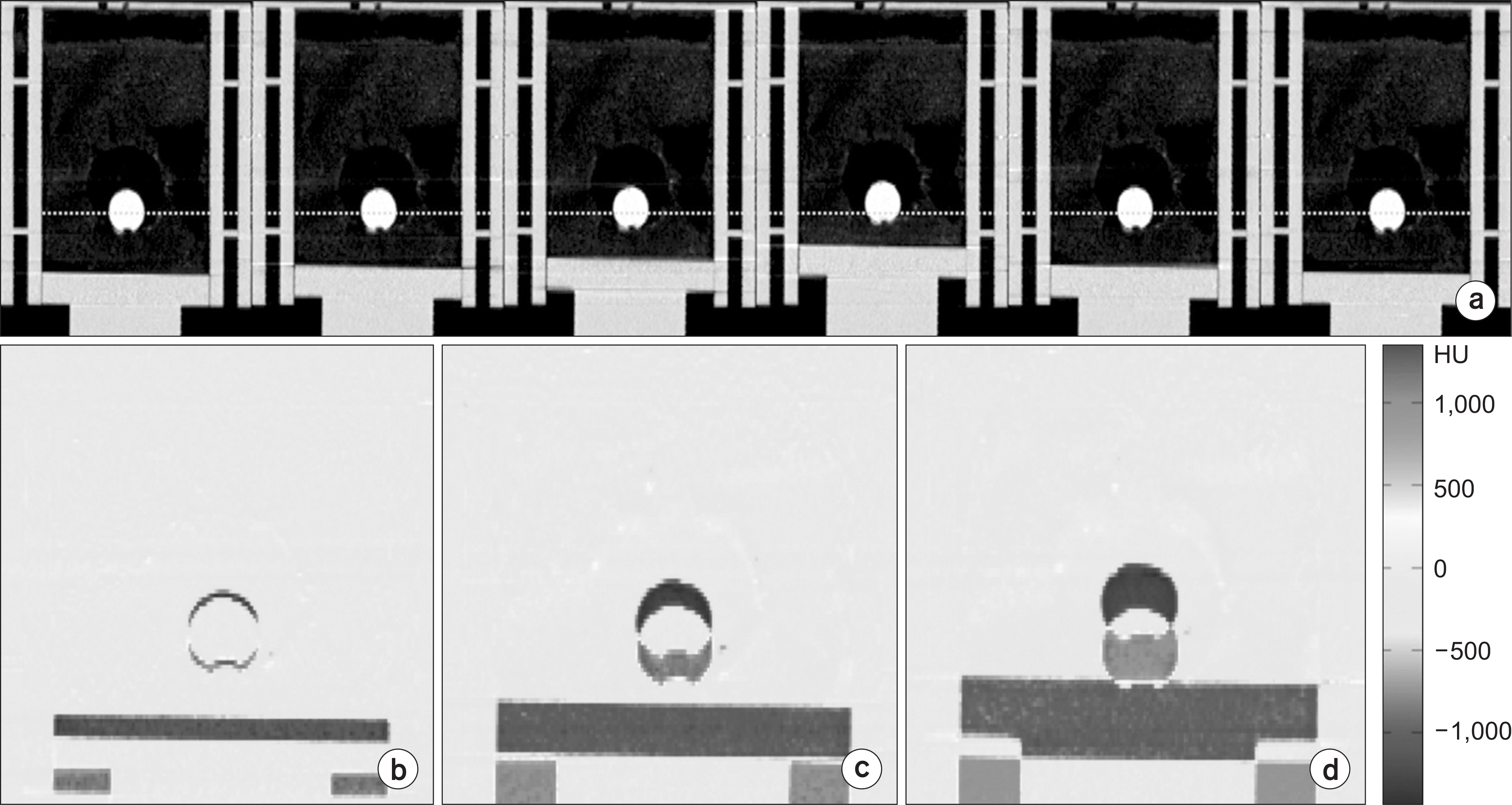Fig. 6.
Example of a phantom four-dimensional computed tomography (4DCT) image of a 10 cm3 tumor. (a) Coronal views of the 4DCT image for setting the 2 cm motion amplitude case. (b~d) Difference between the 4DCT end-inhalation and end-exhalation phase image, (b) setting the 1 cm phantom diaphragm motion case, (c) setting the 2 cm phantom diaphragm motion case, and (d) setting the 3 cm phantom diaphragm motion case.
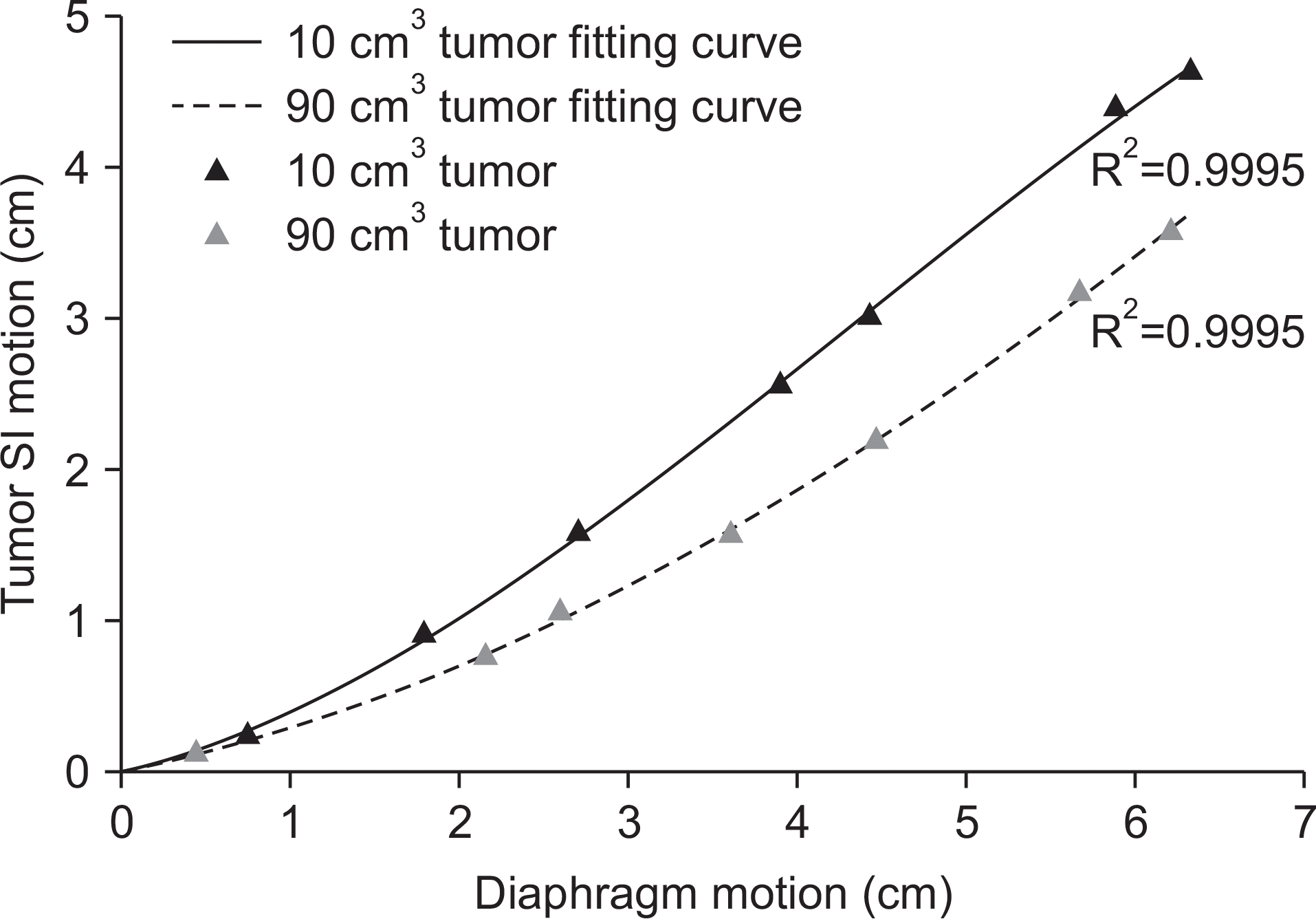Fig. 7.
Diaphragm-tumor correlation curves between the phantom diaphragm motion and tumor motion in the superior-inferior (SI) direction. The colored triangle symbols represent the tumor center-of-mass (COM) positions in the SI direction acquired from four-dimensional computed tomography (4DCT) data, and the colored lines are the fitting curves. On the basis of the tumor COM position from the 4DCT data, the curve fitting was performed using the cubic polynomial method.
Fig. 8.
Four-dimensional computed tomography images for coronal view at the end-inhalation phase for one data set to identify the tumor positions. The red dotted lines describe the tumor surfaces, and the orange arrows represent the distance between the phantom diaphragm and tumor surface. (a) 90 cm3 tumor case, (b) 10 cm3 tumor case.
Fig. 9.
Four-dimensional dose (4D dose) calculation process. Three-dimensional dose (3D dose) distributions are calculated at each phase on the basis of the same treatment planning that is planned on the reference phase (end-exhalation) image of four-dimensional computed tomography. Deformation vector fields (DVFs) between the reference and the other phase images are acquired using the deformable image registration. These DVFs applied the 3D dose distribution, which is dose warping, and the dose distributions deformed by the DVFs were summed with equal weighting.
Fig. 10.
Example of dose distributions of 90 cm3 tumor (phantom motion amplitude of 1 cm) for coronal views. (a) Three-dimensional dose (3D dose) distribution, (b) four-dimensional dose (4D dose) distribution, and (c) distribution of difference between the 3D and 4D dose.
Table 1.
Verification of the phantom diaphragm motion: equation and measured motions.
Table 2.
Tumor trajectories between the end-inhalation and end-exhalation phase images for each tumor size case.
XML Download