Improvement of Analytic Reconstruction Algorithms Using a Sinogram Interpolation Method for Sparse-angular Sampling with a Photon-counting Detector

Dohyeon Kim; Byungdu Jo; Su-Jin Park; Hyemi Kim; Hee-Joung Kim

doi:10.14316/pmp.2016.27.2.105

Journal List > Prog Med Phys > v.27(3) > 1098540

Go to TopGo to Top Go to BottomGo to Bottom

TOOLS

Kim, Jo, Park, Kim, and Kim: Improvement of Analytic Reconstruction Algorithms Using a Sinogram Interpolation Method for Sparse-angular Sampling with a Photon-counting Detector

Original Article

Progress in Medical Physics 2016;27(3):105-110.

Published online: 19 September 2016

DOI: https://doi.org/10.14316/pmp.2016.27.2.105

Improvement of Analytic Reconstruction Algorithms Using a Sinogram Interpolation Method for Sparse-angular Sampling with a Photon-counting Detector

Dohyeon Kim^∗, Byungdu Jo^†, Su-Jin Park^†, Hyemi Kim^†, Hee-Joung Kim^†,

^∗Departments of Radiation Convergence Engineering, Yonsei University, Wonju, Korea

^†Departments of Radiological Science, College of Health Science, Yonsei University, Wonju, Korea

Correspondence: Hee-Joung Kim (hjk1@yonsei.ac.kr) Tel: 82-33-760-2983, Fax: 82-33-760-2562

Received 7 July 201621 September 2016 Accepted 22 September 2016

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Sparse angular sampling has been studied recently owing to its potential to decrease the radiation exposure from computed tomography (CT). In this study, we investigated the analytic reconstruction algorithm in sparse angular sampling using the sinogram interpolation method for improving image quality and computation speed. A prototype of the spectral CT system, which has a 64-pixel Cadmium Zinc Telluride (CZT)-based photon-counting detector, was used. The source-to-detector distance and the source-to-center of rotation distance were 1,200 and 1,015 mm, respectively. Two energy bins (23∼33 keV and 34∼44 keV) were set to obtain two reconstruction images. We used a PMMA phantom with height and radius of 50.0 mm and 17.5 mm, respectively. The phantom contained iodine, gadolinium, calcification, and lipid. The Feld-kamp-Davis-Kress (FDK) with the sinogram interpolation method and Maximum Likelihood Expectation Maximization (MLEM) algorithm were used to reconstruct the images. We evaluated the signal-to-noise ratio (SNR) of the materials. The SNRs of iodine, calcification, and liquid lipid were increased by 167.03%, 157.93%, and 41.77%, respectively, with the 23∼33 keV energy bin using the sinogram interpolation method. The SNRs of iodine, calcification, and liquid state lipid were also increased by 107.01%, 13.58%, and 27.39%, respectively, with the 34∼44 keV energy bin using the sinogram interpolation method. Although the FDK algorithm with the sinogram interpolation did not produce better results than the MLEM algorithm, it did result in comparable image quality to that of the MLEM algorithm. We believe that the sinogram interpolation method can be applied in various reconstruction studies using the analytic reconstruction algorithm. Therefore, the sinogram interpolation method can improve the image quality in sparse-angular sampling and be applied to CT applications.

Keywords: Sinogram interpolation, Computed tomography (CT), Image reconstruction, Low-dose, Photon-counting detector

REFERENCES

1.Kalke M., Siltanen S. Sinogram interpolation method for sparse-angle tomography. Appl Math. 5(3):423–441. 2014.

2.Brooks RA., Weiss GH., Talbert AJ. A new approach to interpolation in computed tomography. J Comput Assisted Tomogr. 2(5):577–585. 1978.

3.Kim D., Park S-J., Jo B., Kim H., Kim H-J. Investigation of sparse-angle view in cone beam computed tomography (CBCT) reconstruction algorithm using a sinogram interpolation method. IFMBE Proceedings. 2015, Canada, pp.74.

4.Siltanen S., Kolehmainen V., Järvenpää S, et al. Statistical inversion for medical x-ray tomography with few radiographs: I. General theory. Phys Med Biol. 48(10):1465–1490. 2003.

5.Lahart MJ. Estimation of reconstructions in computed tomography. J Opt Soc Am. 71(10):1155–1161. 1981.

6.Shikhaliev PM., Xu T., Molloi S. Photon counting CT: Concept and initial results. Med Phys. 32(2):427–436. 2005.

7.Lundqvist M., Cederstrom B., Chmill V., Danielsson M., Hasegawa B. Evaluation of a photon counting X-ray imaging system. IEEE Trans Nucl Sci. 48(4):1530–1536. 2001.

8.Sarkar V., Shi C., Rassiah-Szegedi P, et al. The effect of a limited number of projections and reconstruction algorithms on the image quality of megavoltage digital tomosynthesis. J Appl Clin Med Phys. 10(3):155–172. 2009.

9.Feldkamp LA., Davis LC., Kress JW. Practical cone-beam algorithm. J Opt Soc Am A. 1(6):612–619. 1984.

10.Shepp LA., Vardi Y. Maximum likelihood reconstruction for emission tomography. IEEE Trans Med Imag. 1(2):113–122. 1982.

11.Dempster AP., Laird NM., Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. J R Statist Soc B. 39(1):1–38. 1977.

12.https://en.wikipedia.org/wiki/Signal-to-noise_ratio_(imaging).

13.Bertram M., Wiegert J., Schäfer D., Aach T., Rose G. Directional View Interpolation for Compensation of Sparse Angular Sampling in Cone-Beam CT. IEEE Trans Med Imag. 28(7):1011–1022. 2009.

14.Bertram M., Rose G., Schäfer D., Wiegert J., Aach T. Directional interpolation of sparsely sampled cone-beam CT sinogram data. IEEE Int Symp Biomed Imag. 1:928–931. 2004.

Fig. 1

Flowchart of the proposed sinogram interpolation method.

Fig. 2

Spectral CT system with CZT-based photon-counting detector.

Fig. 3

Illustration of the PMMA phantom containing four materials.

Fig. 4

Restored PMMA phantom sinogram. (a) Without interpolation in 36 views, (b) With interpolation in 36 angular views.

Fig. 5

The reconstruction images of the PMMA phantom with the FDK and MLEM algorithms. (a∼c) Non-enhanced iodine image (23∼33 keV): (a) FDK without the sinogram interpolation method, (b) FDK with the sinogram interpolation method, (c) MLEM (10 iterations). (d∼e) Enhanced iodine image (34∼44 keV): (d) FDK without the sinogram interpolation method, (e) FDK with the sinogram interpolation method, (f) MLEM (10 iterations).

Fig. 6

The SNRs in the reconstruction images by FDK with the sinogram interpolation method, FDK without the sinogram interpolation method, and MLEM (10 iterations) (23∼33 keV).

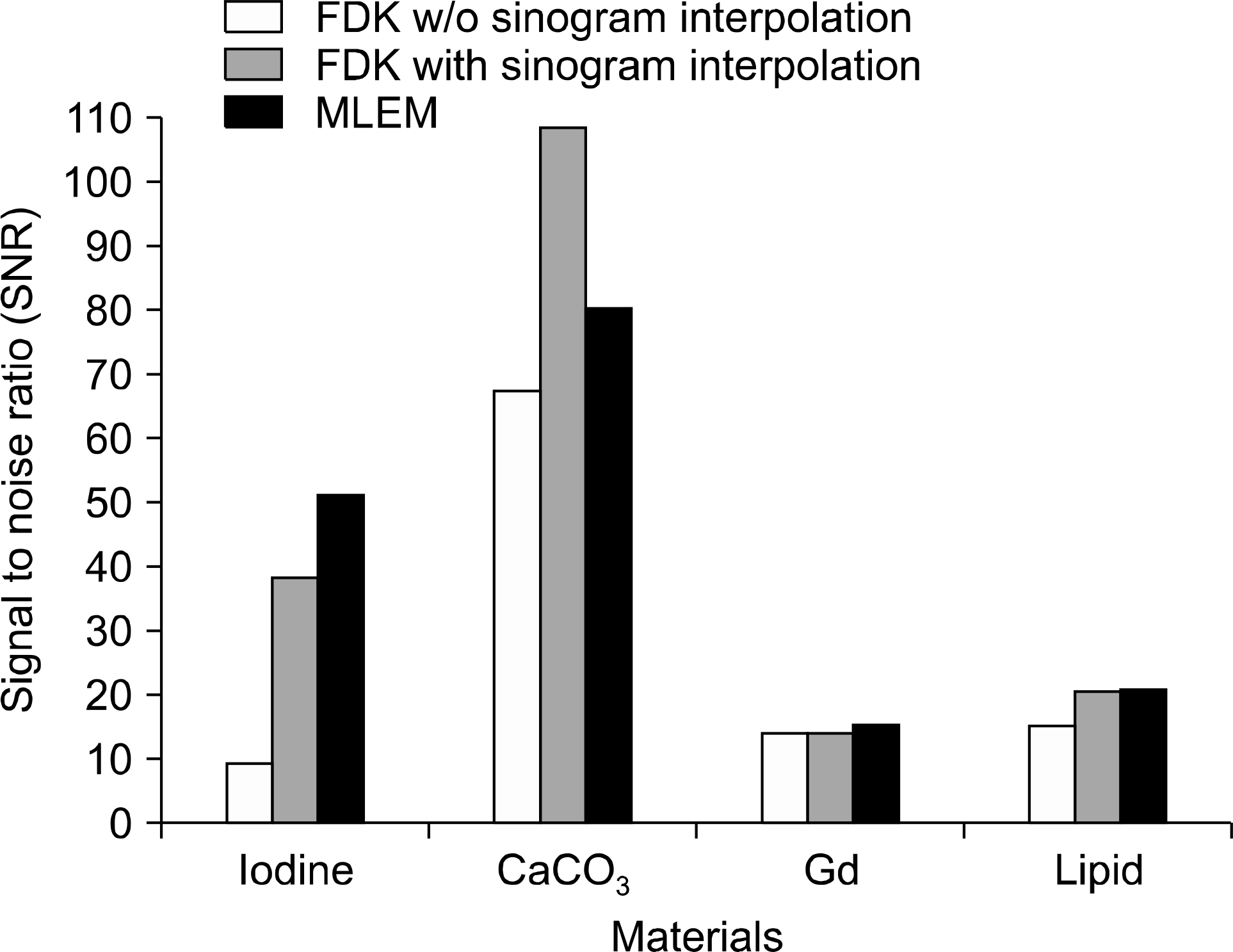
Fig. 7

The SNRs in reconstruction images by FDK with the sinogram interpolation method, FDK without the sinogram interpolation method, and MLEM (10 iterations) (34∼44 keV).

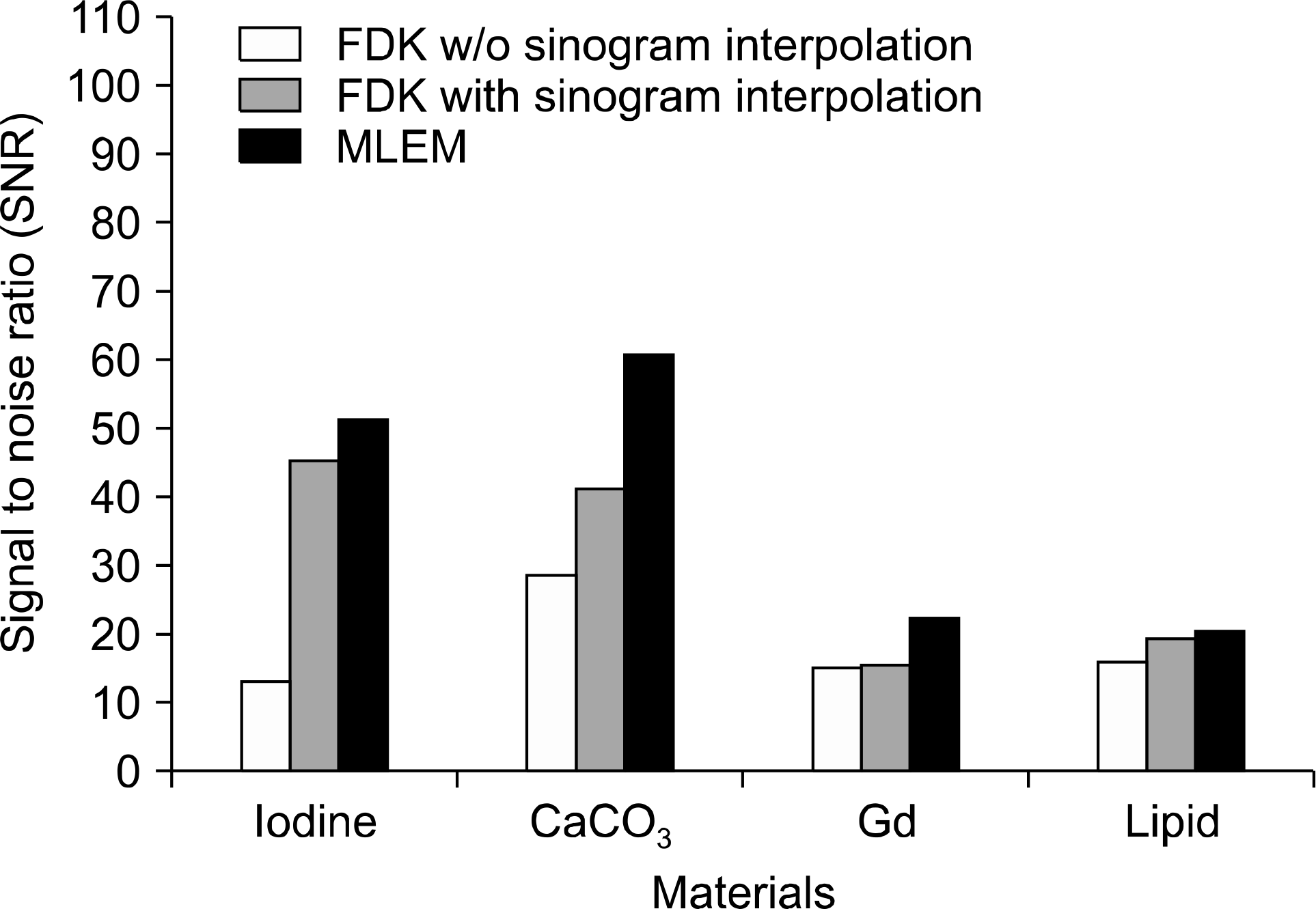
Fig. 8

Time consumption for reconstructing images by FDK with the sinogram interpolation method, FDK without the sinogram interpolation method, and MLEM (10 iterations).

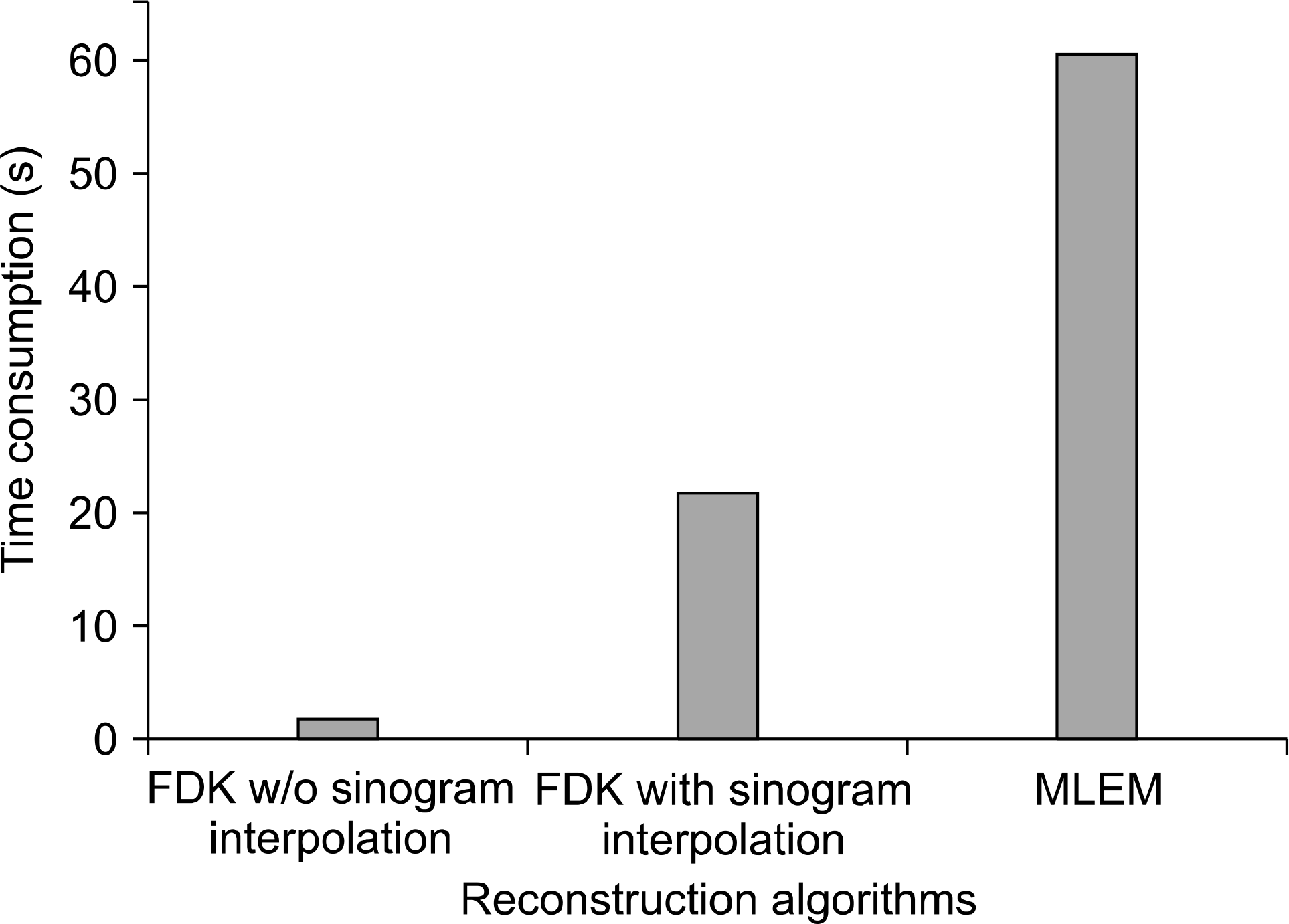
Table 1.

Detailed acquisition parameters of the spectral CT system.

Source to detector distance (SID)	1,200 mm
Source to center of rotation distance	1,015 mm
Detector information
Pixel pitch	0.8 mm
Detector length	51.2 mm
Number of pixels	64×1
Source information	bin 1: 23∼33 keV
	bin 2: 34∼44 keV
Number of projections (angle interval)	36 projections (10^o)
Reconstruction method	1. Reconstruction method –‘FBP’
	2. Filter –‘Ram-lak’

TOOLS

Similar articles