Abstract
Purpose
Among RF pulses, a sinc pulse is typically used for slice selection due to its frequency-selective feature. When a sinc pulse is implemented in practice, it needs to be apodized to avoid truncation artifacts at the expense of broadening the transition region of the excited-band profile. Here a sinc pulse tailored by a new apodization function is proposed that produces a sharper transition region with well suppression of truncation artifacts in comparison with conventional tailored sinc pulses. A multiband pulse designed using this newly apodized sinc pulse is also suggested inheriting the better performance of the newly apodized sinc pulse.
Materials and Methods
A new apodization function is introduced to taper a sinc pulse, playing a role to slightly shift the first zero-crossing of a tailored sinc pulse from the peak of the main lobe and thereby producing a narrower bandwidth as well as a sharper pass-band in the excitation profile. The newly apodized sinc pulse was also utilized to design a multiband pulse which inherits the performance of its constituent. Performances of the proposed sinc pulse and the multiband pulse generated with it were demonstrated by Bloch simulation and phantom imaging.
Results
In both simulations and experiments, the newly apodized sinc pulse yielded a narrower bandwidth and a sharper transition of the pass-band profile with a desirable degree of side-lobe suppression than the commonly used Hanning-windowed sinc pulse. The multiband pulse designed using the newly apodized sinc pulse also showed the better performance in multi-slice excitation than the one designed with the Hanning-windowed sinc pulse.
Conclusion
The new tailored sinc pulse proposed here provides a better performance in slice (or slab) selection than conventional tailored sinc pulses. Thanks to the availability of analytical expression, it can also be utilized for multiband pulse design with great flexibility and readiness in implementation, transferring its better performance.
In comparison with other imaging modalities such as X-ray, computed tomography (CT), ultrasound etc., magnetic resonance imaging (MRI) has unique appealing features of not only offering various image contrasts with anatomical, physiological, and chemical meanings, but also allowing slice-selective 2D imaging as well as 3D tomographic imaging. Especially, MRI capability of slice selection originates from the availability of the frequency-selective spin excitation which some shaped radiofrequency (RF) pulses are able to offer with a well-defined square-like response profile in frequency domain. Among the frequency-selective RF pulses, a sinc pulse is most widely used for slice (or slab) selection not only because it has been well known to obtain a rectangular-window function from a sinc function via Fourier transform, but also because the width of the spin-excited region is well approximated by the RF pulse bandwidth especially in a linear regime at low flip angles (1). As the RF pulse is implemented with a finite length in practice, it is desirable to tailor a sinc pulse with proper apodization in order to avoid truncation artifacts (2). Despite the virtue of apodization to reduce the truncation artifacts, there is a trade-off between the apodization and the sharpness of a transition region in the frequency-response profile of the RF pulse. In other words, stronger apodization of a RF pulse in time domain yields more suppression of truncation artifacts but broader transition region of the pass-band profile in frequency domain.
In this paper a new type of tailored sinc pulse is proposed which utilizes a new apodization function. The newly apodized sinc pulse provides a sharper transition region and less amount of unwanted signals outside the excitation bandwidth in the frequency-response profile than conventional tailored sinc pulses, e.g., using the Hanning apodization function. Design of a multiband pulse based on the newly apodized sinc pulse is also discussed, expecting that its appealing features can be inherited to the multiband pulse designed with it. Performances of the proposed sinc pulse and the multiband pulse generated by it are demonstrated by Bloch simulation and phantom imaging at 3T.
Provided that the apodization function (Apo(t)) is described explicitly, time-dependent expression for a tailored sinc pulse is given by
where t0 is the time of the first zero-crossing and is one-half the width of the central lobe in the sinc function. The apodization function typically tapers the sinc pulse at its edges in order to minimize the truncation artifacts. Common apodization functions including the Hanning and Hamming windows are based on the cosine function, which is (3),
where N is the total number of zero-crossings in the sinc pulse and α is the parameter used to determine the type of apodization. The Hanning and Hamming windows are generated by setting α = 0.5 and 0.46, respectively. When α = 0, Apo(t) = 1 and Eq. [1] then reduces to the original sinc function with no apodization.
While common tailored sinc pulses employ a cosine function as a basic constituent (Eq. [2]), the proposed new apodization function is given by combining two cosine-damped functions, which are represented inside the parentheses in the following:
Here η and β were empirically determined to be 0.2 and 0.3 while optimizing the apodizing performance of Eq. [3] in terms of transition sharpness, side lobes, and bandwidth. It is interesting to note that common apodization functions in Eq. [2] are basically bell shaped (Fig. 1a), whereas the new apodization function has quite a different shape from them as shown in Figure 1b, having two sharp bipolar peaks the positions of which correspond to the two first zero-crossings of the sinc pulse to be apodized (Fig. 2a). This new type of weighting form is mainly attributed to the first cosine-damped function inside the brackets in Eq. [3]. Since β does not exist in the denominator, the first cosine-damped function behaves differently with respect to t from the second cosine-damped function outside the brackets, which is bell-shaped like the conventional apodization functions, and makes the peculiar shape shown in Figure 1b especially having two sharp bipolar peaks at the positions of the two first zero-crossings of the sinc pulse to be apodized (Fig. 2a). As a result of this special weighting, the first zero-crossings of the newly apodized sinc pulse are slightly shifted outward from the central peak of the sinc pulse (Fig. 2b), thereby producing a narrower bandwidth and a sharper transition of the excited-band profile than the most common Hanning-windowed sinc pulse (Fig. 3a, b). These appealing features of the proposed sinc pulse might be expected from the fact that the bandwidth of a sinc pulse is inversely proportional to the width of the first zero-crossing through Fourier transform to a good approximation in the low-flip angle regimes.
Recently, as one of the attractive fast imaging methods, simultaneous multi-slice imaging techniques have been proposed using a multiband pulse for simultaneous excitation of multiple slices (456). There are several ways of designing a multiband pulse including a Sinnar-Le-Roux (SLR) algorithm (7). Among them, the approaches that provide an analytical expression for pulse generation are easy to implement and flexible in changing the pulse parameters such as phase, bandwidth, and the number of bands (8910). They simply write a multiband pulse as a sum of single-band pulses with the phase of each pulse shifted in a scheduled way. For example, when based on a sinc pulse, a multiband pulse can be expressed as
where the MB in the subscript was used as an abbreviation of multiband and φn is the phase of the nth sinc pulse. According to Eq. [4], φn determines the location of the nth excitation band in the frequency domain due to the linear and frequency-shift properties of Fourier transform, whereas the sinc function determines the shape of the slice (or slab) profile. To minimize the truncation effects on multi-slice profiles, therefore, the sinc function in Eq. [4] needs to be tailored with proper apodization. In this case, the newly apodized sinc pulse proposed in Eqs. [1] and [3] can be utilized and Eq. [4] is then rewritten for the newly tailored multiband pulse as
Simulation was carried out for testing the performance of the proposed sinc pulse with new apodization and the four-band multiband pulse designed with it. Excitation profiles were obtained by Bloch simulation in MATLAB (Mathworks, R2011a, Natick, MA, USA) using three sinc pulses with no apodization, Hanning apodization, and new apodization, respectively, and corresponding three four-band multiband pulses. A three-lobe sinc pulse with four zero-crossings was used with 4-ms pulse length and thus 1-kHz pulse bandwidth.
For the simulation using the single-band tailored sinc pulses for spin excitation, the entire frequency range of all the assumed spin isochromats was set to 3 kHz so that it can fully cover the excitation bandwidth which approximately corresponds to the pulse bandwidth. The flip angle for spin excitation was assumed to be 90°. The full-width-half-maximum (FWHM) of the excitation profiles was measured to see whether the apodization-induced broadening of the excitation profile affects the excitation bandwidth. The area of the excitation profile outside the FWHM was also calculated by numerical integration to evaluate the effects of side lobes and broadening of the excitation profile simultaneously, which can be a good indicator of how much unwanted signal existing outside the excitation bandwidth smears into a slice through slice selection because the FWHM is used to determine the magnitude of the slice-selective gradient in practice. Lastly, the transition sharpness of the excitation profile was measured by calculating the width between the frequencies at 5% and 95% of the maximum amplitude of the excitation profile.
In the case of using the multiband pulses for spin excitation, each excitation bandwidth and the separation width between two consecutive excitation bands were set to be same as 1 kHz. The whole frequency range across all the assumed spin isochromats was assumed to be 10 kHz. The pulse length was set to 4 ms as was in the simulation using the single-band sinc pulse.
To confirm the Bloch simulation results of the proposed sinc pulse and the multiband pulse designed with it, experiments were performed using a spherical water phantom on a 3T whole-body scanner manufactured by ISOL technology of Korea.
First, the newly apodized sinc pulse was used for slab selection in conventional 3D gradient-echo imaging. For comparison, the Hanning-windowed and unapodized sinc pulses were also tested with the same experimental setup. Scan parameters were: TE/TR = 4.8/9.1 ms, FOV = 250 × 250 × 120 mm3, flip angle = 8°, matrix size = 512 × 256 × 120, and slab thickness = 50 mm.
Next, a four-band pulse designed with the newly apodized sinc pulse was applied for slab selection in the same 3D gradient-echo imaging sequence. Four-band pulses based on the Hanning-windowed and unapodized sinc pulses were also tested for comparison purposes. Scan parameters were: TE/TR = 20/30 ms, FOV = 256 × 256 × 32 mm3, flip angle = 14°, matrix size = 64 × 64 × 104, and slab thickness = 26 mm. While the image was highly defined along the slab-selective direction with a spatial resolution of 0.31 mm in order to clearly demonstrate the apodization effects on the excitation profile, especially on the region between two consecutive bands as well as the transition region of each band, the data in other two directions were obtained with a relatively low spatial resolution of 4 mm.
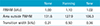
Figure 3 shows the excitation profiles produced by the single-band tailored sinc pulses (Fig. 3a, b) and the four-band multiband pulses designed with them (Fig. 3c, d) with no apodization (black), Hanning apodization (green), and the new apodization (red). As shown in Figure 3a and 3b, while the newly apodized sinc pulse delivered the excitation profile with side lobes of much less amplitude than the unapodized sinc pulse but a slightly larger amplitude than the Hanning-windowed sinc pulse, it produced sharper transition (0.36 kHz) and narrower FWHM (1.02 Hz) in the excited-band profile than the Hanning-windowed sinc pulse which yielded 0.5 kHz and 1.10 kHz for the transition width and FWHM, respectively (Table 1). The area of the excitation profiles outside the FWHM was 131.6, 127.9, and 106.3 [a.u.] for the cases with no apodization, Hanning apodization, and new apodization, respectively, implying that unwanted signals existing outside the excitation bandwidth least contributes to the inside of a slice in the case of the new tailored sinc pulse.
On the other hand, as shown in Figure 3c and 3d, the performance of a single-band pulse was well inherited to a multiband pulse designed with it. In other words, each excitation-band profile of the multiband pulse is almost as same as that of the single-band pulse used for designing the multiband pulse. Therefore, as was the case in the single-band sinc pulses, the multiband pulse designed with the new tailored sinc pulse demonstrated more desirable performance in simultaneous four-slice selection than the one generated by the Hanning-windowed sinc pulse.
The phantom experiments well confirmed the results of Bloch simulation. In Figures 4 and 5, phantom images were demonstrated for the three cases with Hanning apodization, new apodization, and no apodization, having the slab-selective orientation as a horizontal direction. To better illustrate the difference between the three cases, 1D magnitude profiles were obtained along the horizontal lines drawn with yellow color and plotted as black, green, and red lines for the three cases of no apodization, Hanning apodization, and new apodization, respectively.
As shown from the images as well as the 1D profiles in Figure 4, the new tailored sinc pulse yielded a sharper excitation profile than the Hanning-windowed one, well suppressing the side-lobe artifacts in comparison to the unapodized one. These experimental results of the single-band sinc pulses are in exact agreement with the simulation results shown in Figure 3a and 3b.
In the case of the multiband pulses, the phantom imaging results were also consistent with the simulation results. As expected from the number of bands of the multiband pulse used, four regions were excited and visualized corresponding to the four pass-bands of the multiband pulse (Fig. 5a). With of the multiband pulse made of unapodized sinc pulses, side-lobe effects as banding artifacts are clearly seen between the excited regions, whereas the side-lobe artifacts are barely recognized but at the expense of broadening of the excited regions when using the multiband pulse designed with the Hanning-windowed sinc pulse. The most desirable situation occurred in the use of the multiband pulse based on the new tailored sinc pulse, showing that the side-lobe artifacts were well suppressed with a sharper transition of each excitation band than the Hanning-window-based multiband pulse.
In this article a new type of window function was analytically proposed for better apodization of a sinc pulse. The newly apodized sinc pulse demonstrated less intrusion of unwanted signals existing outside the excitation bandwidth into the inside of a slice, also showing a sharper transition of the excitation profile, than a conventional Hanning-windowed sinc pulse. Moreover, such desirable features of the new tailored sinc pulse were well transferred to the multiband pulse design using this new tailored sinc pulse as a basic component. Another to-be-noted virtue of the multiband pulse design proposed here was the availability of the analytical expression of the multiband pulse to be designed, which allows for readiness in implementation and flexibility in changing pulse parameters such as phase, bandwidth, and the number of bands, etc.
An important issue in the multiband pulse design is how to reduce the peak RF power, especially as the number of bands increases, and this can be effectively achieved by scrambling the phase of each excitation band in generation of a multiband pulse. When an analytical form is given for the multiband pulse design like Eq. [4] or [5], an easy way for the phase scrambling is to make a phase table using the Bloch simulation so that the phase of each excitation band is randomly distributed to minimize the resulting RF peak amplitude (910). Another possible approach is to utilize a frequency-modulation pulse in the multiband pulse design, which intrinsically produces non-linear phase distribution in the excitation bandwidth. For example, the hyperbolic-secant pulse can be a candidate for that purpose because it creates a non-linear phase profile delivering an excellent excitation profile (1112).
In conclusion, the new tailored sinc pulse proposed here provides a better performance in slice (or slab) selection than conventional tailored sinc pulses. Thanks to the availability of analytical expression, it can also be utilized for multiband pulse design with great flexibility and readiness in implementation. As demonstrated from both simulation and experiment, the better performance of the proposed tailored sinc pulse is well maintained in the multiband pulse generated using it. It is expected that the multiband pulses designed with the proposed tailored sinc pulse will be beneficial in many applications of simultaneous multi-slice imaging.
Figures and Tables
 | Fig. 1Apodization functions used for tailoring a three-lobe sinc pulse to reduce truncation artifacts. (a) Hanning- (solid line) and Hamming-apodization (dashed line) functions. (b) The new apodization function which has quite a different waveform from conventional bell-shaped apodization functions. |
 | Fig. 2(a) Illustration of how the new apodization function is applied to a three-lobe sinc pulse. The positions of the two sharp bipolar peaks of the new apodization function correspond to the two first zero-crossings of the original sinc pulse, shifting the first zero-crossing slightly outward from the original positions (gray arrows). (b) Comparison of sinc pulses with no apodization (black), Hanning apodization (green), and new apodization (red). While the Hanning-windowed and unapodized sinc pulses coincide in the position of the first zero-crossings, the newly apodized sinc pulse has slightly shifted first zero-crossings as expected from (a). For better demonstration, the region (0.2 ≤ t ≤ 0.3 ms) around the first-zero crossing in left side was zoomed-in at the bottom in (a) and (b). |
 | Fig. 3Bloch simulation results acquired using (a, b) tailored sinc pulses and (c, d) four-band multiband pulses for spin excitation. (a, b) The newly apodized sinc pulse yielded sharper transition region and narrower bandwidth at the expense of slightly larger side lobes than the Hanning-windowed sinc pulse. The amount of unwanted signals existing outside the bandwidth was the least with the newly apodized sinc pulse (Table 1). (c, d) Inheriting the characteristics of the single-band sinc pulse in each band, the four-band multiband pulse designed with the newly apodized sinc pulse showed better performance than the one based on the Hanning-windowed sinc pulse. |
 | Fig. 4(a) Images of a sphere water phantom acquired using three single-band sinc pulses with no apodization, Hanning apodization, and new apodization. (b) 1D magnitude profiles extracted along the horizontal yellow lines in (a). In agreement with the simulation results, the new tailored sinc pulse showed better performance with well suppression of side-lobe artifacts than the Hanning-windowed sinc pulse in terms of transition sharpness. |
 | Fig. 5(a) Phantom images acquired using three four-band multiband pulses designed with three sinc pulses with no apodization, Hanning apodization, and new apodization, respectively. (b) 1D magnitude profiles extracted along the horizontal yellow lines in (a). As expected from the number of bands, four selective regions were successfully excited. As was in the Bloch simulation, the multiband pulse generated by the newly apodized sinc pulse gave a better performance than the one designed using the Hanning-windowed sinc pulse. These results also demonstrate that the performance of a single-band pulse is well transferred to the multiband pulse based on that single-band pulse. |
Acknowledgments
This work was supported by NRF-2010-0025744, IBS-R015-D1, and the Advanced MRI Study Group of KSMRM.
References
1. Pauly J, Nishimura D, Macovski A. A k-space analysis of small-tip-angle excitation. 1989. J Magn Reson. 2011; 213:544–557.
2. MacFall JR, Charles HC, Prost R. Truncated sinc slice excitation for 31P spectroscopic imaging. Magn Reson Imaging. 1990; 8:619–624.
3. Bernstein S, King KF, Zhou XJ. Handbook of MRI pulse sequences. Burlington, MA: Elsevier;2004.
4. Moeller S, Yacoub E, Olman CA, et al. Multiband multi-slice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fMRI. Magn Reson Med. 2010; 63:1144–1153.
5. Feinberg DA, Setsompop K. Ultra-fast MRI of the human brain with simultaneous multi-slice imaging. J Magn Reson. 2013; 229:90–100.
6. Wu X, Schmitter S, Auerbach EJ, Moeller S, Ugurbil K, Van de Moortele PF. Simultaneous multislice multiband parallel radiofrequency excitation with independent slice-specific transmit B1 homogenization. Magn Reson Med. 2013; 70:630–638.
7. Pauly J, Le Roux P, Nishimura D, Macovski A. Parameter relations for the Shinnar-Le Roux selective excitation pulse design algorithm [NMR imaging]. IEEE Trans Med Imaging. 1991; 10:53–65.
8. Goelman G, Leigh JS. Multiband adiabatic inversion pulses. J Magn Reson A. 1993; 101:136–146.
9. Goelman G. Two methods for peak RF power minimization of multiple inversion-band pulses. Magn Reson Med. 1997; 37:658–665.
10. Wong E. Optimized phase schedules for minimizing peak RF power in simultaneous multi-slice RF excitation pulses. In : Proceedings of the 20th Annual Meeting of ISMRM; Melbourne, Australia. 2012.
11. Park JY, DelaBarre L, Garwood M. Improved gradient-echo 3D magnetic resonance imaging using pseudo-echoes created by frequency-swept pulses. Magn Reson Med. 2006; 55:848–857.
12. Park JY, Garwood M. Spin-echo MRI using pi/2 and pi hyperbolic secant pulses. Magn Reson Med. 2009; 61:175–187.




 PDF
PDF ePub
ePub Citation
Citation Print
Print


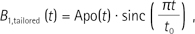
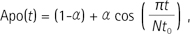
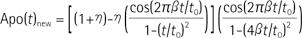
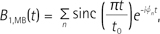
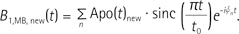
 XML Download
XML Download