Prodrug Kinetics
When a prodrug is administered orally, it undergoes complicate processes of absorption, distribution, metabolism, and excretion. To understand these processes for metabolites, Cummings and Martin published results on the excretion and accrual of drug metabolites in 1963.[
4] This provides the basis for the pharmacokinetics of drug and its metabolites and can be readily applied to study the pharmacokinetics of prodrug. Since then, many theoretical analyses and reviews, related to prodrug pharmacokinetics, have been published.[
5678910] A thorough understanding of prodrug kinetics is daunting and may be achieved using sophisticated physiologically based pharmacokinetic (PBPK) modeling.[
1112]
To get some insight pertinent to prodrug kinetics, we consider a simple scheme for the fate of a prodrug (P) after intravenous administration (
Fig. 1). A fraction of the prodrug (
f) is metabolized and produces a parent drug (D) with a first-order formation rate constant,
kf(D). The drug (D) may be further metabolized to a daughter metabolite (DM
1) or excreted. The elimination rate constant of the parent drug,
kel(D), is expressed by the sum of the formation rate constant of the daughter metabolite,
kf(DM1), and the urinary excretion rate constant,
kex(D). More than one metabolite may be formed with a formation rate constant,
kf(PM2), and then excreted with a rate constant,
kex(PM2). Otherwise, a fraction of the drug is excreted into urine as unchanged form (P) with a rate constant,
kex(P). The overall elimination rate constant of the prodrug,
kel(P), is the sum of
kf(D),
kf(PM2), and
kex(P). No matter how complex the pathways may appear, the time course for the change of metabolite amount can be described by a general relationship: rate of change of metabolite amount in body = rate of formation − rate of elimination. [
56] However, a full mathematical description of this model is still complex and difficult to solve. We will further simplify this model to have clear understanding of the factors influencing the amount of parent drug in the body.
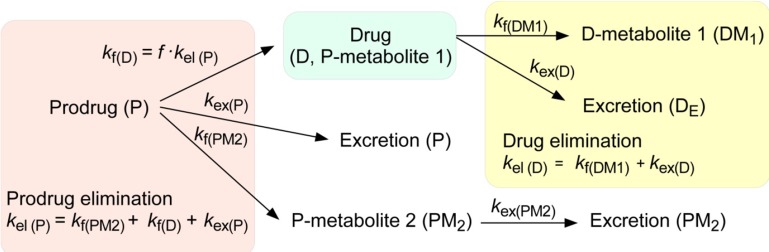 | Figure 1A model to describe the kinetics of a prodrug and its metabolites. The prodrug (P) is metabolized or excreted unchanged according to the elimination rate constant (kel(P)). The drug (D) is eliminated according to the elimination rate constant (kel(D)). See text for details.
|
A basic model for prodrug kinetics
Consider a simple case of a two-step consecutive first-order irreversible reaction:
This model provides the basis for developing more complex models. Thus it is crucial to understand this reaction kinetics thoroughly for further study. Here, we use simple notations for the sake of clarity. We can set up the following three differential equations to describe the change in amounts of A, B, and C over time.
At t = 0, A = A0 and B = C = 0, and A + B + C = A0 at all times. The Eq. (1) can be solved immediately to give
Substituting Eq. (4) into Eq. (2), we get
Eq. (5) can be solved simply by noting that
By multiplying both sides of Eq. (5) by ek2t and using the above relationship, we get
If k1 ≠ k2, integration of Eq. (6) from t = 0 to t gives
In the special case when k1 = k2, Eq. (6) can reduce to
Then, the integrated expression becomes
The expression for C can be obtained using the mass balance relationship, C = A0 − A − B,
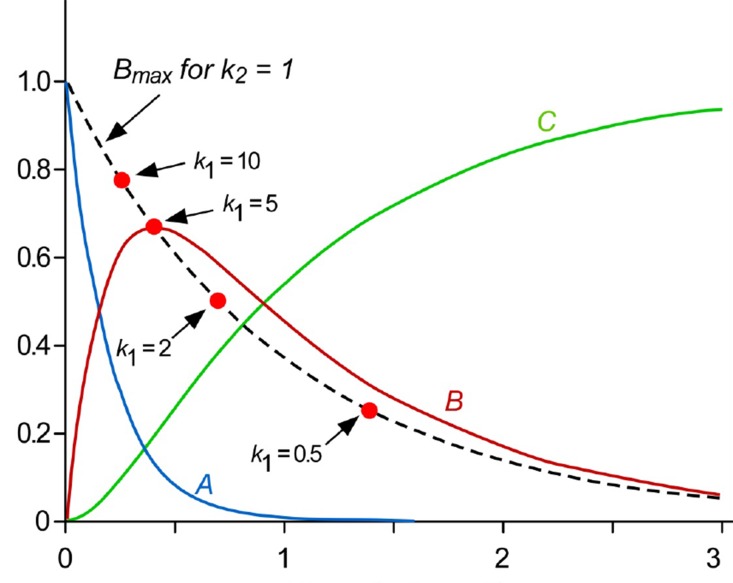
Figure 2 shows a typical amount-time profile of each species for the consecutive first-order irreversible reaction. The amount of A decreases at the normal exponential rate characteristic of a first-order decay curve (blue line). The amount of B follows a bi-exponential profile, first rising and then declining (red line). The amount of C continuously increases and reaches a plateau (green line). This profile is useful for quantifying absorption and elimination processes of drug as well as formation and elimination processes of metabolite.[
1314]
To calculate the maximum amount of B (Bmax) and the time to reach the peak (tmax), we take the derivative of Eq. (7), set the derivative, dB/dt, to zero, and rearrange to obtain
Take the natural logarithm of both sides and solve for tmax to get
The resulting Bmax at tmax then becomes
Using Eq. (10), we obtain
From Eq. (11), we get
Therefore,
In
Figure 2, we also visualized the Equations (11), (13), and (14) to show that
tmax decreases and
Bmax increases as the ratio of
k1 to
k2 increases (dashed line). In other words, when
k2 is smaller than
k1, the amount of A quickly decreases while the amount of
B increases rapidly, reaches a maximum at a shorter time, and then falls off with time.
Plasma concentration profile after intravenous administration of prodrug
Now consider a case for the intravenous administration of prodrugs (P) in which all the prodrugs are converted to active drugs (D) and then eliminated. In this case, the first-order formation rate constant for D, kf(D), is equal to the elimination rate constant for P, kel(P). The parameter kel(D) represents the first order elimination rate constant for D. The rate of change of D in the blood is determined by the difference between the formation and the elimination rates. Because the level of each species in the blood is measured in concentration ([D] = D/VD, where VD is the volume of distribution for D), it is convenient to express Eq. (7) with the same unit. Then, using new notations (k1 → kf(D); k2 → kel(D)), we get
where VP is the volume of distribution for P, and [P]0 is the initial concentration of P in the blood.
When plasma concentrations are measured as a function of time, the area under the concentration-time curve (AUC) is of great interest in pharmacokinetics. We can derive a useful relationship between AUC and clearance (CL = k×V; volume/time in unit) by solving Eq. (2) using a concentration-time integral method. Writing Eq. (2) in new notations and taking the integral of both sides, we get
Because D is not present in the body initially or at infinity, the left side becomes zero. Rearranging Eq. (16) and substituting kel(P) = CL(P)/VP and kel(D) = CL(D)/VD, we get
This ratio is useful to study metabolic pathway and pharmacokinetic interactions.[
891013]
Elimination rate-limited (ERL) and formation rate-limited (FRL) metabolism
As shown in Eq. (15), the plasma drug concentration, [
D], at any given time is expressed by two exponential functions. Depending on the relationship between the prodrug and drug elimination rates, one term can become more dominant than the other. For a more detailed discussion, we consider two limiting situations. In the first situation, formation is a much faster process than elimination (ERL metabolism:
kf(D) >
kel(D)). In the second situation, formation proceeds much more slowly than elimination (FRL metabolism:
kf(D) <
kel(D)). To help understand the underlying kinetics, we simulated these situations to draw semi-logarithmic plots of plasma concentration versus time using Eq. (15) (
Fig. 3).
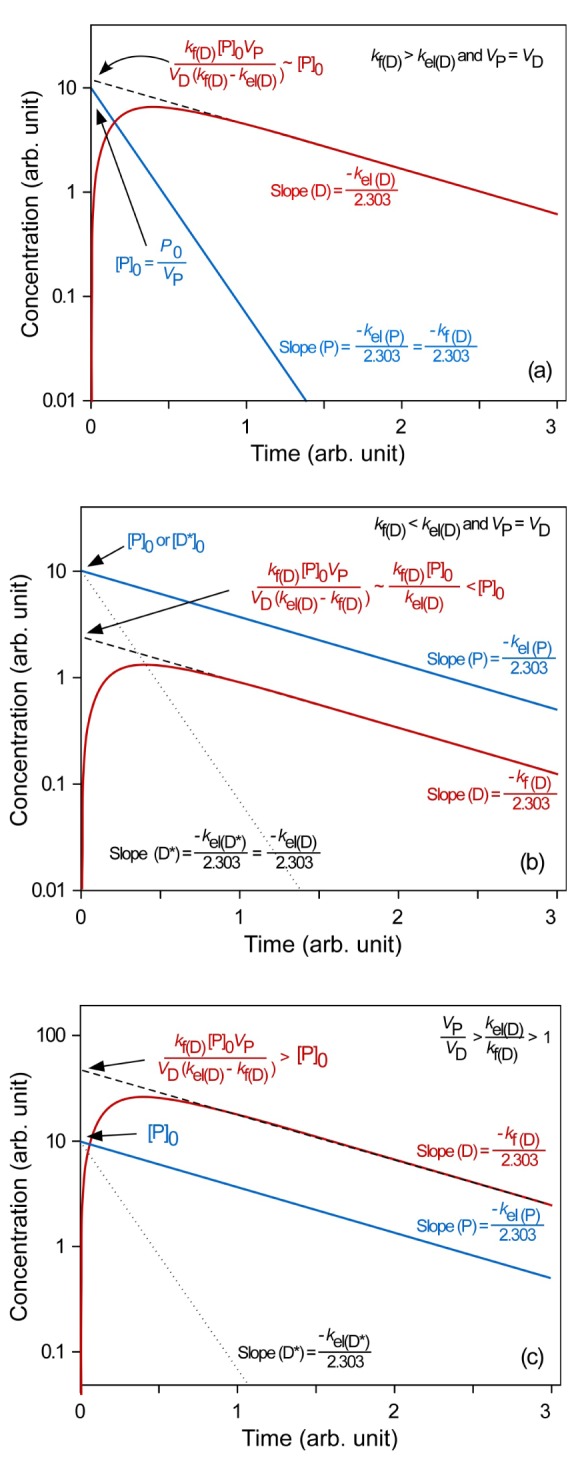 | Figure 3Semi-logarithmic concentration-time profile of a prodrug (P; blue line) and its formed metabolite (parent drug, D; red line). Simulations were performed using Microsoft Excel for three cases: (a) ERL metabolism where kf(D) > kel(D): kf(D) = 5, kel(D) = 1, and VD = VP = 1, (b) FRL metabolism where kf(D) < kel(D): kf(D) = 1, kel(D) = 5, and VD = VP = 1, and (c) FRL metabolism for VP/VD > kel(D)/kf(D) > 1: kf(D) = 1, kel(D) = 5, and VD = 0.05. VP = 1, and A0 = 10. Back extrapolation (dashed line; plotted using Eq. (19) or (21)) of the elimination phase slope (red line) provides an estimate of [D]0. The dotted line was plotted using Eq. (23) for the direct intravenous administration of a preformed (or synthesized) parent drug (D*) with the initial amount of D* (D*0) = 10 in (b) and 0.5 in (c). See text for details.
|
In ERL metabolism, at large time, the first term approaches zero because kf(D) > kel(D), and Eq. (15) reduces to
Taking the logarithm to the base 10 of Eq. (18), we get
Thus, the semi-logarithmic plots of plasma concentration versus time become linear with a slope of
kel(D)2.303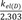
at large time. Back extrapolation (dashed line) of the elimination phase slope (red line) provides an estimate of [D]
0, which is the intercept of
kf(D)VP[P]0VD(kf(D)−kel(D))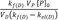
(
Fig. 3a). When
kf(D) >>
kel(D) and V
P = V
D, the intercept can be further reduced to [P]
0.
This situation is commonly encountered in the metabolism of many prodrugs.[
1015] An example is the metabolism of an antitrypanosomal compound (OSU-36) after an intravenous administration of its ester prodrug (OSU-40) to rat. The hydrolysis of OSU-40 was fast, and its concentrations declined rapidly with short half-life (4.8 min). Whereas, the concentrations of OSU-36, hydrolyzed from OSU-40, declined slowly with the half-life of 41.9 min. This was close to the elimination half-life of the preformed OSU-36 (43.9 min), directly administered to the systemic circulation by an intravenous injection.[
15]
In FRL metabolism (kf(D) < kel(D)), at large time, Eq. (15) can be
reduced in a similar way to give
and
The slope and intercept of the semi-logarithmic plot of plasma concentration versus time are
kf(D)2.303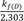
and
kf(D)VP[P]0VD(kel(D)−kf(D))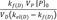
, respectively (
Fig. 3b). In the elimination phase, thus, the concentration of the parent drug is governed by the prodrug formation rate, not by the prodrug elimination rate. Since
kf(D) <
kel(D), the intercept can be further reduced to
The plasma prodrug concentration, [P], at any given time is easily obtained from Eq. (4), and its final semi-logarithmic expression is
In equations (21) and (23), it is worthwhile to note that the slopes are the same, that is, the concentrations of the parent drug and prodrug decline in parallel (
Fig. 3b). Because the parent drug is eliminated almost as soon as it is formed, the elimination rate is approximately equal to the formation rate. The above equation can also be used to plot the plasma concentration-time profile of a preformed D (D*) directly administered to the systemic circulation by an intravenous injection (dotted line). From
Figure 3b, we can easily figure out that the half-life of the formed parent drug (ln 2/
kf(D)) in the elimination phase is longer than that of the preformed parent drug (ln 2/
kel(D*)). The half-life of the formed parent drug reflects that of the prodrug (ln 2/
kel(P) = ln 2/
kf(D)).
The FRL metabolism is less encountered in prodrug kinetics but occasionally in metabolite kinetics.[
101316] One interesting example is the metabolism of 3′-azido-2′,3′-dideoxy-5′-O-oxalatoylthymidine (AZT-Ac) to zidovudine, [3′-azido-2′,3′-dideoxythymidine (AZT)].[
16] Only AZT was detected in plasma, indicating that the prodrug is rapidly hydrolyzed in vivo with a high elimination rate constant. Thus, the first step looks like proceeding according to ERL-metabolism. However, the concentrations of AZT metabolized from AZT-Ac (t
1/2 = 2.16 h) declined more slowly than those of AZT from preformed AZT (t
1/2 = 0.96 h). This means that the metabolic pathway proceeds according to FRL metabolism (
kf(AZT) <
kel(AZT)), as discussed above. This discrepancy may be explained by the presence of multiple pathways for AZT-Ac elimination (small f in
Fig. 1) or by the presence of another intermediate between AZT-Ac and AZT. Because AUC for AZT metabolized from AZT-Ac is slightly larger than that for AZT from preformed AZT at the same intravenous dose, the latter explanation looks more plausible.
In FRL metabolism, it is interesting to consider one more situation where
VP/
VD >
kel(D)/
kf(D) > 1, or CL
(P) > CL
(D). As shown in
Figure 3c, the intercept for the parent drug ([D]
0) is greater than that for the prodrug ([P]
0). This situation is encountered in the metabolic conversion of propranolol to naphthoxylactic acid (NLA) after single intravenous and oral doses.[
17] The AUC of NLA was two times greater than that of propranolol after an intravenous dose of propranolol (4 mg) and ten times after a single oral dose (20 or 80 mg). This can be easily explained if the volume of distribution of NLA is much smaller than that of propranolol. The volumes of distribution of basic drugs are often larger than 100 L, while those of their acidic metabolites are close to 10~20 L.[
13] Thus, this situation is expected to be common when a basic prodrug is converted to an acidic parent drug.
We described the prodrug kinetics for the simplest situation: formation and sequential elimination. We can consider a more complicated model to account for more realistic situations but will lose simplicity by including more terms in equations. A more detailed discussion is beyond the scope of this tutorial. For further study, we recommend to read articles and book chapters in the References section.

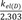 at large time. Back extrapolation (dashed line) of the elimination phase slope (red line) provides an estimate of [D]0, which is the intercept of kf(D)VP[P]0VD(kf(D)−kel(D))
at large time. Back extrapolation (dashed line) of the elimination phase slope (red line) provides an estimate of [D]0, which is the intercept of kf(D)VP[P]0VD(kf(D)−kel(D))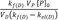 (Fig. 3a). When kf(D) >> kel(D) and VP = VD, the intercept can be further reduced to [P]0.
(Fig. 3a). When kf(D) >> kel(D) and VP = VD, the intercept can be further reduced to [P]0.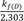 and kf(D)VP[P]0VD(kel(D)−kf(D))
and kf(D)VP[P]0VD(kel(D)−kf(D))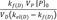 , respectively (Fig. 3b). In the elimination phase, thus, the concentration of the parent drug is governed by the prodrug formation rate, not by the prodrug elimination rate. Since kf(D) < kel(D), the intercept can be further reduced to
, respectively (Fig. 3b). In the elimination phase, thus, the concentration of the parent drug is governed by the prodrug formation rate, not by the prodrug elimination rate. Since kf(D) < kel(D), the intercept can be further reduced to



 PDF
PDF ePub
ePub Citation
Citation Print
Print



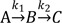
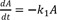
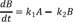
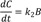
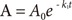
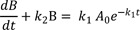
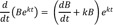
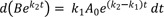
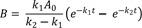
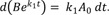 .
.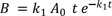 .
.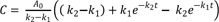
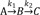
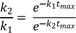
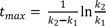
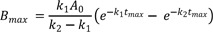
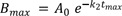
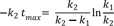
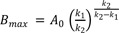
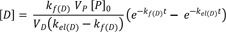
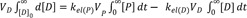 .
.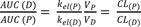 .
.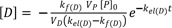 .
.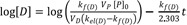
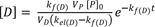
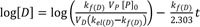 .
.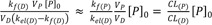
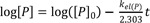
 XML Download
XML Download