Abstract
Purpose
This study aimed to measure the bilateral differences of facial lines in spherical coordinates from faces within a normal range of asymmetry utilizing cone-beam computed tomography (CBCT).
Materials and Methods
CBCT scans from 22 females with normal symmetric-looking faces (mean age 24 years and 8 months) were selected for the study. The average menton deviation was 1.01±0.66 mm. The spherical coordinates, length, and midsagittal and coronal inclination angles of the ramal and mandibular lines were calculated from CBCT. The bilateral differences in the facial lines were determined.
It is not unusual for healthy individuals to have minimal asymmetry of the face which does not cause any esthetic or functional problems.1-6 The range of acceptable minimal asymmetry should be understood prior to diagnosing problematic asymmetry that needs surgical intervention for esthetic and functional rehabilitation.
Researchers, using three-dimensional computed tomography (3D CT), have found that bilateral differences in some facial lines contribute to facial asymmetry.7-11 The distance or inclination of the lines connecting condyle landmarks and gonion landmarks (ramus length, ramal inclination from a frontal view, ramal inclination from a lateral view) and the distance of the line connecting the gonion and the menton (mandibular body length) might contribute to mandibular asymmetry.7,11 The facial lines can be more clearly defined by their length and vertical and horizontal angle in a spherical coordinate system.12
Spherical coordinate systems are used for various purposes such as astronomy and geology. For example, in geology, a spherical coordinate system describes a flying object over the earth with its distance from the center of the earth and its latitude and longitude. Symmetry of objects in 3D space can be also evaluated using a spherical coordinate system.13-18
For defining a facial line in 3D human structure, the spherical coordinate system can be modified to length, midsagittal and coronal inclinations, which are angles of the line relative to the midsagittal and coronal reference planes.12
This study aimed to obtain bilateral differences of facial lines from normal symmetric-looking faces without distinctive asymmetry in spherical coordinates, so this study's findings could provide a reference in the evaluation of facial asymmetry.
Twenty-two CBCT scans were selected for this study. The CBCT scans had been obtained from female patients (average age 24 years 8 months: age range from 18 years 3 months to 31 years 9 months) who had undergone surgical extraction of lower third molars and had needed CBCT scans for localization of the inferior alveolar nerve canal in relationship with the third molars.
The selection criteria of the study subjects were as follows; age of 18 years old or more, the mandible scanned including condyles and gonions by CBCT, class I occlusion, no plastic surgery history, and no distinctive facial asymmetry on clinical examination.
The average menton deviation of the subjects was 1.01±0.66 mm, which was measured as the distance of the menton from the midsagittal reference plane on CBCT. Since the study subjects had no distinctive facial asymmetry on clinical examination and the menton deviation was less than 2 mm,19,20 they were considered to have normal symmetric faces.
CBCT scans had been acquired using MercuRay (Hitachi, Tokyo, Japan) with a 512×512 matrix, 120 kV, and 15mA. The scanning time was 9 seconds. The field of view (FOV) had a 15 cm diameter in a globe shape. Five hundred twelve DICOM data were obtained with slice thickness of 0.29 mm. The acquired DICOM data were inputted into a personal computer. Using the CBCT data, 3D images were reconstructed by V-works 4.0+V-surgery software (Cybermed Co., Seoul, Korea). A multiplanar reformatted image, a volumetric model, and a surface-rendered model of a CBCT scan, which were completely interfaced with each other in the software, were constructed in V-works 4.0. The landmarks were defined on the volumetric model with the guidance of the multiplanar reformatted image.
Table 1 shows the anatomical landmarks, reference planes, and facial lines used for this study. Three orthogonal reference planes, the horizontal (xy plane), midsagittal (yz plane), and coronal (xz plane) reference planes were established. The horizontal reference plane was first established using right Po, left Po, and left Or.7,21 The midsagittal reference plane was then formed perpendicular to the horizontal reference plane and passing through Na and Dent.22 The coronal reference plane was perpendicular to both the midsagittal and the horizontal reference planes passing through Dent.22 The condylar landmarks were identified as the most superior (Cdsup), lateral (Cdlat), and posterior (Cdpost) points of the condylar head. The gonion landmarks were identified as the most inferior (Goinf), lateral (Golat), and posterior (Gopost) points of the gonion area. The menton (Me) was defined as the most inferior point on the mandibular symphysis (Table 1, Fig. 1).
All image data and surface-rendered models were transferred to the V-surgery program (Cybermed Co., Seoul, Korea), where the rectangular coordinates (|x|, y, z) of the landmarks were acquired. |x| was the distance from the midsagittal reference plane, y was the distance from the coronal reference plane, and z was the distance from the horizontal reference plane; |x| was set to absolute values.
The facial lines, ramal height (RH: line Cdsup-Goinf), ramal lateral (RL: line Cdlat-Golat), ramal posterior (RP: line Cdpost-Gopost), and mandibular body (MB: line Gopost-Me) were established relative to the landmarks.7,11 The side of the face on which Me was placed was identified as the deviated side, while the contralateral side of the face was considered to be the opposite side. The rectangular coordinates of the starting landmarks of the facial lines, Goinf, Golat, and Gopost, were obtained. The bilateral differences of the starting landmarks of the facial lines (dx, dy, dz) were obtained and their means were calculated, where (dx, dy, dz) was (xdeviated-xopposite, ydeviated-yopposite, zdeviated-zopposite). The menton was excluded because one point of the menton was used for the bilateral lines for MB in each individual (Table 1).
The alternate spherical coordinates of the facial lines, RH, RL, RP, and MB, were obtained from the rectangular coordinates of the landmarks. As for RL, (xcd-xgo, ycd-ygo, zcd-zgo), (xcd, ycd, zcd) was for Cdlat, and (xgo, ygo, zgo) was for Golat. When x=xcd-xgo, y=ycd-ygo, and z=zcd-zgo, the alternate spherical coordinates (v, θ, ϕ) were calculated as below:
for θ, ϕ in radian measure (θrad=θ°×π/180), where v was the distance of the lines; θ, midsagittal inclination, was the angle inclination from the midsagittal reference plane; ϕ, coronal inclination, was the angle inclination from the coronal reference plane.12
The spherical coordinates of the facial lines were acquired on the deviated and opposite sides. The means of the spherical coordinates of the deviated and opposite sides were compared by a paired t-test. Null hypotheses of no difference were rejected if the p-values were less than 0.05. The mean and standard of the bilateral differences (dv, dθ, dϕ) between the deviated and opposite sides were obtained, where (dv, dθ, dϕ) was (vdeviated-vopposite, θdeviated-θopposite, ϕdeviated-ϕopposite) (Fig. 2). Statistical analyses were performed using SPSS version 15.0 software (SPSS, Chicago, IL, USA).
The bilateral differences of the starting landmarks of the facial lines (dx, dy, dz) between the deviated side and opposite side were obtained. The bilateral differences of the starting landmarks were (-0.08±3.01 mm, -1.08±3.8 mm, 0.29±3.36 mm) for Golat, (0.56±3.39 mm, 0.31± 3.36 mm, 1.80±3.22 mm) for Gopost, and (0.48±3.23 mm, 0.18±3.18 mm, 0.90±3.04 mm) for Goinf (Table 2).
There was no statistically significant difference between the spherical coordinates of the deviated and opposite sides. The bilateral differences of the facial lines in the spherical coordinate system (dv, dθ, dϕ) were (-0.62±3.69 mm, -0.86±2.18°, 1.28±3.14°) for RH, (-2.10±3.24 mm, -0.88±2.07°, -0.42±3.52°) for RL, (-1.29±2.64 mm, -1.45±3.58°, -0.39±4.53°) for RP, and (-0.09±2.46 mm, -0.93±2.72°, -0.52±2.26°) for MB (Table 3).
Accurate diagnosis is essential for ensuring a good treatment plan and postoperative evaluation for facial asymmetry. Three-dimensional CT has an advantage over two-dimensional (2D) cephalometric radiographs in depicting 3D human anatomic structure. Three-dimensional CT depicts the human face without superimposition, magnification, or distortion of anatomic structures, all of which are inherent on 2D cephalometric radiographs. This study aimed to measure the bilateral differences of the facial lines in spherical coordinates from the faces with a normal range of asymmetry utilizing 3D CBCT.
In this study, CBCT was used for 3D CT analysis of facial asymmetry in normal individuals. Studies have reported that the linear accuracy of CBCT was similar to that of CT.23,24 The mean difference between the actual measurement on the skull and measurement on CT was 0.83% in the study by Cavalcanti and Vannier23 and -1.13 ±1.47% in the study of Periago et al.24 The accuracy of the linear measurement on CBCT was acceptable for 3D facial analysis.
This study showed that there were minimal differences on the starting landmarks of the facial lines in all of the study subjects (Table 2). No perfect symmetry of facial lines in spherical coordinates was seen in any study subject. All of the subjects had somewhat asymmetrical facial lines, though there was no statically significant difference between the deviated and opposite sides. Considering only the mean value, the facial lines of the deviated side were shorter and more erect toward the midsagittal reference plane than those of the opposite side, the RH and RL of the opposite side were more erect toward the coronal reference plane than that of the deviated side, and the RP and MB of the deviated side were more erect toward the coronal reference plane than those of the opposite side (Table 3).
Several researchers have developed standard values for the normal range of asymmetry by obtaining bilateral differences of landmarks in rectangular coordinates for hard or soft tissue analysis on 3D CT.21,22,25,26 However, there has been no study on the normal range of asymmetry of facial lines. The spherical coordinate systems were applied for this study to obtain the normal range of asymmetry of the facial lines, which might be critical contributing factors to facial asymmetry.7,11
In conclusion, the normal range of facial asymmetry in the spherical coordinate system in this study should be useful as a reference for planning treatment of facial asymmetry and for evaluation of facial asymmetry of the postoperative state. This study was limited by the inclusion of females only, whose faces are small enough for the condyles and chin to be projected in a 15 cm diameter FOV of CBCT, the maximum FOV that the machine allowed. The sample size in this study was only 22 female subjects. Further study with a larger sample size of male and female subjects using CBCT with a wider FOV is needed.
Figures and Tables
 | Fig. 13D reconstruction image of CBCT. A. Three orthogonal reference planes are established. B-D. Condylar landmarks and gonion landmarks and the menton are identified. |
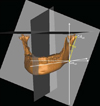 | Fig. 2Spherical coordinates of a facial line, the ramal lateral (RL) is seen. v is the distance of the lines; θ, the midsagittal inclination, is the angle inclination from the midsagittal reference plane; ϕ, the coronal inclination, is the angle inclination from the coronal reference plane. The mandible is cropped for understanding. |
References
1. Alavi DG, BeGole EA, Schneider BJ. Facial and dental arch asymmetries in Class II subdivision malocclusion. Am J Orthod Dentofacial Orthop. 1988. 93:38–46.

2. Peck S, Peck L, Kataja M. Skeletal asymmetry in esthetically pleasing faces. Angle Orthod. 1991. 61:43–48.
3. Ferrario VF, Sforza C, Miani A Jr, Serrao G. Dental arch asymmetry in young healthy human subjects evaluated by Euclidean distance matrix analysis. Arch Oral Biol. 1993. 38:189–194.

4. Ferrario VF, Sforza C, Miani A, Tartaglia G. Craniofacial morphometry by photographic evaluations. Am J Orthod Dentofacial Orthop. 1993. 103:327–337.

5. Farkas LG. Anthropometry of the head and face. 1994. 2nd ed. New York: Raven Press;103–111.
6. Ras F, Habets LL, van Ginkel FC, Prahl-Andersen B. Method for quantifying facial asymmetry in three dimensions using stereophotogrammetry. Angle Orthod. 1995. 65:233–239.
7. Hwang HS, Hwang CH, Lee KH, Kang BC. Maxillofacial 3-dimensional image analysis for the diagnosis of facial asymmetry. Am J Orthod Dentofacial Orthop. 2006. 130:779–785.

8. Baek SH, Cho IS, Chang YI, Kim MJ. Skeletodental factors affecting chin point deviation in female patients with class III malocclusion and facial asymmetry: a three-dimensional analysis using computed tomography. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 2007. 104:628–639.

9. Tuncer BB, Ataç MS, Yüksel S. A case report comparing 3-D evaluation in the diagnosis and treatment planning of hemimandibular hyperplasia with conventional radiography. J Craniomaxillofac Surg. 2009. 37:312–319.

10. Vezzetti E, Calignano F, Moos S. Computer-aided morphological analysis for maxillo-facial diagnostic: a preliminary study. J Plast Reconstr Aesthet Surg. 2010. 63:218–226.

11. Kim EJ, Palomo JM, Kim SS, Lim HJ, Lee KM, Hwang HS. Maxillofacial characteristics affecting chin deviation between mandibular retrusion and prognathism patients. Angle Orthod. 2011. 81:988–993.

12. Yoon SJ, Wang RF, Hwang HS, Kang BC, Lee JS, Palomo JM. Application of spherical coordinate system to facial asymmetry analysis in mandibular prognathism patients. Imaging Sci Dent. 2011. 41:95–100.

13. Fisher NI, Lewis T, Embleton BJ. Statistical analysis of spherical data. 1993. Cambridge: Cambridge University Press;17–28.
14. Leong P, Carlile S. Methods for spherical data analysis and visualization. J Neurosci Methods. 1998. 80:191–200.

15. Thaller B. Advanced visual quantum mechanics. 2005. New York: Springer;1–56.
16. Allen TR, Kupfer JA. Application of spherical statistics to change vector analysis of landsat data: Southern Appalachian spruce-fir forests. Remote Sens Environ. 2000. 74:482–493.

17. Yu P, Grant PE, Qi Y, Han X, Ségonne F, Pienaar R, et al. Cortical surface shape analysis based on spherical wavelet. IEEE Trans Med Imaging. 2007. 26:582–597.
18. Cuartero A, Armesto J, Rodriguez PG, Arias P. Error analysis of terrestrial laser scanning data by means of spherical statistics and 3D graphs. Sensors (Basel). 2010. 10:10128–10145.

19. Haraguchi S, Takada K, Yasuda Y. Facial asymmetry in subjects with skeletal Class III deformity. Angle Orthod. 2002. 72:28–35.
20. Ferguson JW. Cephalometric interpretation and assessment of facial asymmetry secondary to congenital torticollis. The significance of cranial base reference lines. Int J Oral Maxillofac Surg. 1993. 22:7–10.

21. Park SH, Yu HS, Kim KD, Lee KJ, Baik HS. A proposal for a new analysis of craniofacial morphology by 3-dimensional computed tomography. Am J Orthod Dentofacial Orthop. 2006. 129:600.e23–600.e34.

22. Katsumata A, Fujishita M, Maeda M, Ariji Y, Ariji E, Langlais RP. 3D-CT evaluation of facial asymmetry. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 2005. 99:212–220.

23. Cavalcanti MG, Vannier MW. Quantitative analysis of spiral computed tomography for craniofacial clinical applications. Dentomaxillofac Radiol. 1998. 27:344–350.

24. Periago DR, Scarfe WC, Moshiri M, Scheetz JP, Silveira AM, Farman AG. Linear accuracy and reliability of cone beam CT derived 3-dimensional images constructed using an orthodontic volumetric rendering program. Angle Orthod. 2008. 78:387–395.

25. Yoon SJ, Lim HJ, Kang BC, Hwang HS. Three dimensional CT analysis of facial asymmetry. Korean J Oral Maxillofac Radiol. 2007. 37:45–51.
26. Hwang HS, Yuan D, Jeong KH, Uhm GS, Cho JH, Yoon SJ. Three-dimensional soft tissue analysis for the evaluation of facial symmetry in normal occlusion individuals. Korean J Orthod. 2012. 42:56–63.




 PDF
PDF ePub
ePub Citation
Citation Print
Print





 XML Download
XML Download