This article has been
cited by other articles in ScienceCentral.
Abstract
Clearance is a key concept in pharmacokinetics, but it is not easy to understand for beginners. This tutorial aims to help beginners by using the analogy of a vacuum cleaner clearing the dust from the air in a room. The air, the volume of the air, the dust and the vacuum cleaner are used to represent the plasma, the volume of distribution, the drug and the eliminating organ, respectively, in the human body. Because the capacity of a vacuum cleaner (eliminating organ) is an inherent feature that is independent of the concentration of dust (drug), the elimination rate (eliminated amount/time) of dust (drug), which is proportional to its concentration in the air (plasma), cannot reflect this inherent capacity correctly. Clearance estimates the volume of the solvent (air or plasma) cleared by the organ per unit time rather than the amount of the solute (dust or drug) removed. Therefore, clearance has the unit of volume/time. Just as the air is cleared of dust, but is not eliminated by the vacuum cleaner, the plasma is cleared of drug, but is not eliminated from the human body.
Keywords: clearance, pharmacokinetics, vacuum cleaner
Introduction
The concept of clearance (CL)in physiology was first introduced in 1928[
1] and was redefined in pharmacokinetics as the ratio of the dose and the area under the concentration–time curve(AUC).[
2] This tutorial aims to help beginners understand the concept of CL. The term ‘beginner’indicates those who have just entered postgraduate courses on clinical pharmacology and pharmaceutical industry employees who wish to understand some basic terms in pharmacokinetics,regardless of their undergraduate major.
Unless you work as part of the nephrology team in a hospital, CL is the type of term that may be heard only in physiology classes in medical or pharmacy schools. Those who majored in biological sciences in their undergraduate courses have almost always answered ‘No’ when asked ‘Have you ever heard of the term CL?’ in my pharmacokinetics classes for graduate students (personally, I do not understand why physiology, the pillar of biology, is neglected in their curricula). However, even for medical or pharmacy school graduates, the concept of CL learned in a physiology or pharmacology class is hard to understand at first. TCP (Transl Clin Pharmacol) has therefore published a comprehensive article written by Holford and Yim[
3] that discusses the relationships of CL with dose, concentration and elimination rate using examples of commonly used drugs. In contrast to Holford's article, this tutorial focuses on how CL differs from the elimination rate using an example that students may experience in their daily lives.
In 1988, I was a medical student taking a physiology class. The concept of CL described in the renal physiology chapter of the textbook was a puzzle to my colleagues and me. The description was written in ordinary medical terms, but the sentence composed of these plain terms dumped us into a maze. During winter vacation after that semester, I spent days trying to understand the concept of CL on my own. After days of thinking, I devised my own explanatory scenario to overcome this little devil, CL. This tutorial therefore originated from a medical student's frustration about 30 years ago, so I hope it can now help similarly frustrated young readers.
Analogy of a vacuum cleaner
Instead of talking about CL as a pharmacokinetic parameter, let us initiate our discussion in an empty room with a vacuum cleaner. The human body is replaced by the room and the plasma by the air in that room (
Table 1).
The vacuum cleaner is a household commodity. How can you best describe its performance or capacity to clean the room air? The rpm and suction power of the motor? Whichever metric is chosen, it should be something that can represent its capacity to perform its unique role–cleaning. Let us suppose that your vacuum cleaner is used to clean the air (to eliminate dust in the air) instead of the carpet in your room.
How does a vacuum cleaner work? Conventional vacuum cleaners have dust bags inside. When the motor starts to run, the air sucked in passes through the dust bag, where dust particles are caught. You are in a room with dusty air (dust particles 100 ng/L = 100 µg/m
3 of air). A brand new vacuum cleaner that has never been used is switched on to clean the air. After 30 minutes of vacuuming, you switch it off and disassemble it to weigh the dust collected into the bag (
Fig. 1). The amount of dust in the bag is 200 ng. How would you state the cleaning capacity of your cleaner now? Because your vacuum filtered 200 ng of dust per 30 min, you may first say that it cleans dust at a rate of 400 ng/h (= 200 ng/0.5 h): The amount of dust captured per unit time, what a simple answer!
Does this metric really express the cleaning capacity? We assume that the capacity of a vacuum or any other mechanical instrument should be constant regardless of conditions, unless these are extreme. What if the room air is more or less dusty than the first room (100 ng/L)? To clarify this issue, you move to the next room, where the dust concentration is 50 ng/L (half that of the first) and repeat the same test using the same vacuum cleaner but with a new dust bag. As a result, you collect 100 ng of filtered dust particles after 30 minutes of vacuuming (= 200 ng/h), only half that collected in the first room. Therefore, if we regard the capacity of a mechanical device as an inherent feature that does not change, the dust mass captured per unit time cannot be used to describe the vacuum's capacity. In other words, we want the vacuum's capacity to be expressed in a metric that is constant, regardless of the dustiness of the air.
CL has the unit of volume/time
Now, why don't we focus on the solvent (air) instead of the solute (dust)? Instead of asking how much dust was removed, ask how much air was cleared! This shift of viewpoint may resolve the issue of the capacity metric being changed by the dust concentration.
The volume of air cleared per time in the first room is easily calculated from the amount of dust cleared per time (200 ng/0.5 h) as follows: 200 ng/0.5 h = 400 ng/h = 4 L (air) × 100 ng/L (dust concentration)/h. Thus, 4 L/h of air was cleared in the first room. Then, let us compare this with the case of the second room. The amount of air cleared per time in the second room is 100 ng/0.5 h (=200 ng/h). It is also converted as follows: 100 ng/0.5 h = 200 ng/h = 4 L (air) × 50 ng/L (dust concentration in the second room)/h. Therefore, the amount of air cleared in the second room was also 4 L/h. The volume of air cleared per unit time in both rooms was identical regardless of the dust concentration (
Table 2). Therefore, the capacity of the vacuum cleaner is best expressed in terms of cleared air volume per unit time rather than filtered dust amount per unit time. This exemplifies the concept of CL: dust (solute) CL by the vacuum cleaner is expressed in terms of air (solvent) volume per time, which remains constant as long as the vacuum operates normally (the author is not sure whether a vacuum cleaner's capacity really follows first-order kinetics, but this tutorial assumes so for teaching purposes).
From the above example, CL may be defined as follows: the capacity of an organ to eliminate a substance dissolved in plasma expressed as the volume of plasma cleared of the substance per time. Just substitute the dust, air, and vacuum cleaner with the drug, plasma, and eliminating organ, respectively.
Let us return to the vacuum cleaner. To measure CL more precisely, we need to collect the dust for a longer time (much longer than 30 min). It would be best to collect the dust until no more is detected in the air. One problem in calculating the capacity for clearing the air (CL) is that the concentration of dust in the air also changes over time. In the previous example, we assumed that the concentration remained constant for the 30-min interval, which is not a perfectly correct assumption. However, the example seems to work when the decrease in the dust concentration of the room air within the 0.5 h interval is negligible (when the room is large enough). However, when the vacuum cleaner is run until all dust particles are eliminated, the decrease in the dust concentration of the air should be taken into consideration.
To calculate the capacity (CL) of the vacuum, we use the following equation in our thinking process.
When the vacuum works long enough (eternally) to eliminate all of the dust particles in the air:
The problem of time-varying (or decreasing-with-time) dust concentration multiplied by ∞ h is solved by the classical ‘mensuration by parts' method. The right side of the above equation is rewritten as:
Readers may now see that this is identical to the well-known equation ‘Dose = CL × AUC’. Those who are not familiar with this formula are recommended to read some pharmacokinetics textbooks.
The vacuum cleaner does not eliminate the air, but rather, it clears the air by filtering out dust particles; the air simply passes through the vacuum cleaner. Therefore, the CL by the vacuum cleaner cannot be higher than its air flow, i.e., the capacity of the motor of the vacuum cleaner. Likewise, the blood CL by any eliminating organ cannot be higher than its blood flow. (The issue of CL estimation methods of using plasma or blood concentration has been discussed elsewhere.[
4]) The CL of a vacuum cleaner would equal zero regardless of its air flow when the dust bag is torn. Likewise, hepatic or renal CL would equal zero regardless of its plasma flow if its metabolic enzymes or glomeruli cannot clear the target substance. Lastly, the volume of the room in which the vacuum cleaner operates may be compared to the volume of distribution of drug.
Summary
From this example of a dusty room where a vacuum (and its motor) is running, we can imagine the human body with an eliminating organ and a heart. The CL by a vacuum cleaner is constant regardless of the dust concentration in the room air, just as the drug CL by a human organ is constant regardless of the drug concentration (under the assumption of linear kinetics). CL is measured in volume/time, as you can see from the vacuum cleaner example.
The clearing capacity (CL) of a vacuum cleaner (eliminating organ) is an inherent feature that is independent of the concentration of dust (drug).
The elimination rate (eliminated amount/time) of dust (drug) is proportional to its concentration in the air (plasma); therefore, it cannot reflect the inherent capacity correctly.
CL estimates the volume of the solvent (air or plasma) cleared by the organ per unit time instead of the amount of the solute (dust or drug).
The relationship is: elimination rate = amount/time = concentration × volume/time = concentration × CL
Figures and Tables
Figure 1
Mechanism of a vacuum cleaner. The amount of dust filtered into the bag was measured after running the cleaner for 30 min.
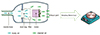
Table 1
The human body compared to a room to understand the concept of clearance (CL) in pharmacokinetics

|
Features |
Room |
Human body |
|
Volume |
Volume of air in the room |
Volume of distribution |
|
Organ |
Vacuum cleaner |
Liver or kidney |
|
Fluid flowing through the organ |
Air (L/min) |
Plasma (L/min) |
|
Fluid inlet |
Nozzle and hose |
Organ's artery |
|
Fluid outlet |
Exhaust port |
Organ's vein |
|
Driving force for the flow |
Motor |
Heart |
|
Eliminated substance |
Dust particles |
Drug molecules |
|
Mechanism of elimination |
Filtration (filter bag) |
Excretion or metabolism |
|
Elimination rate determined by |
Flow, particle size and conc
|
Flow, CLint and conc
|
|
Clearance determined by |
Flow and particle size |
Flow and CLint
|
Table 2
Comparison of the air-clearing capacity of a vacuum cleaner measured in two rooms. CL is the only appropriate metric for the capacity, which should be identical for the two rooms

|
First Room |
Second Room |
Unit |
|
Dust concentration in the air |
100 ng/L |
50 ng/L |
amount/volume |
|
Dust filtered in 30 min |
200 ng |
100 ng |
time |
|
Elimination rate for dust |
400 ng/h |
200 ng/h |
amount/time |
|
Cleared air in 30 min |
2 L (200 ng = 100 ng/L × 2 L) |
2 L (100 ng = 50 ng/L × 2 L) |
volume/time |
|
Cleared air in unit time (CL) |
4 L/h |
4 L/h |
volume/time |
Acknowledgement
The author appreciates CEED communications for their help in the illustrations in this tutorial.
The author also appreciates many students who gave valuable feedbacks on this example of a vacuum cleaner.
References
1. Möller E, McIntosh JF, Van Slyke DD. Studies of urea excretion II. Relationship between urine volume and the rate of urea excretion by normal adults. J Clin Invest. 1928; 6:427–465.
2. Hoenig V, Schück O. Hepatic clearance theory and applications. Rev Czech Med. 1956; 2:62–66.
3. Holford N, Yim DS. Clearance. Transl Clin Pharmacol. 2015; 23:42–45.

4. Atkinson AJ Jr. Pitfalls in the calculation of hemodialysis clearance and in the assessment of dialysis efficacy. Transl Clin Pharmacol. 2016; 23:153–156.





 PDF
PDF ePub
ePub Citation
Citation Print
Print


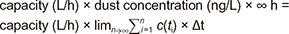



 XML Download
XML Download