Journal List > Transl Clin Pharmacol > v.24(2) > 1082643

TOOLS
Choi: Statistical basis for pharmacometrics: random variables and their distribution functions, expected values, and correlation coefficient
Original Article

Translational and Clinical Pharmacology 2016;24(2):66-73.

Published online: 15 June 2016

DOI: https://doi.org/10.12793/tcp.2016.24.2.66

Statistical basis for pharmacometrics: random variables and their distribution functions, expected values, and correlation coefficient

Kyungmee Choi∗, +,

Division of Mathematics, College of Science and Technology, Hongik University at Sejong, Jochiwon, Sejong 30016, South Korea

∗Correspondence: K. Choi; Tel: +82-44-860-2237, Fax: +82-44-863-2648, E-mail: kmchoi@hongik.ac.kr

+ This work was supported by the 2016 Hongik University Academic Research Support Fund.

Received 22 February 2016       Accepted 29 April 2016

Copyright © 2016 Korean Society for Clinical Pharmacology and Therapeutics

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

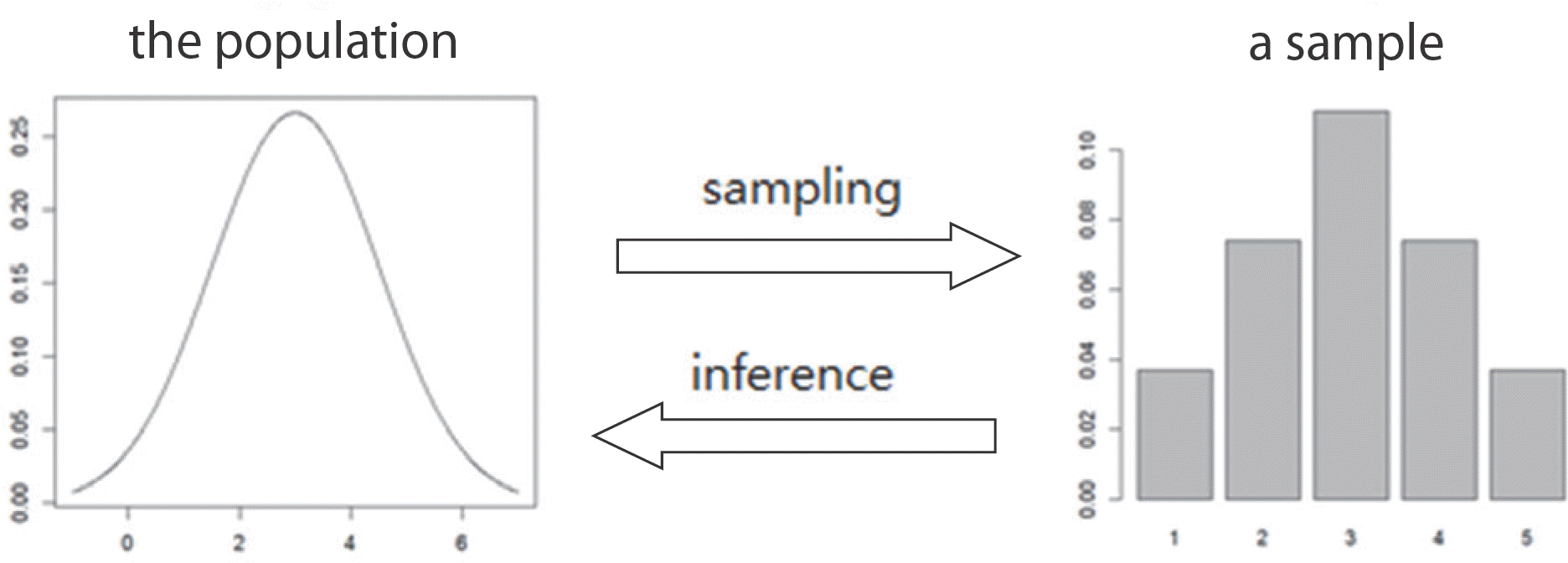
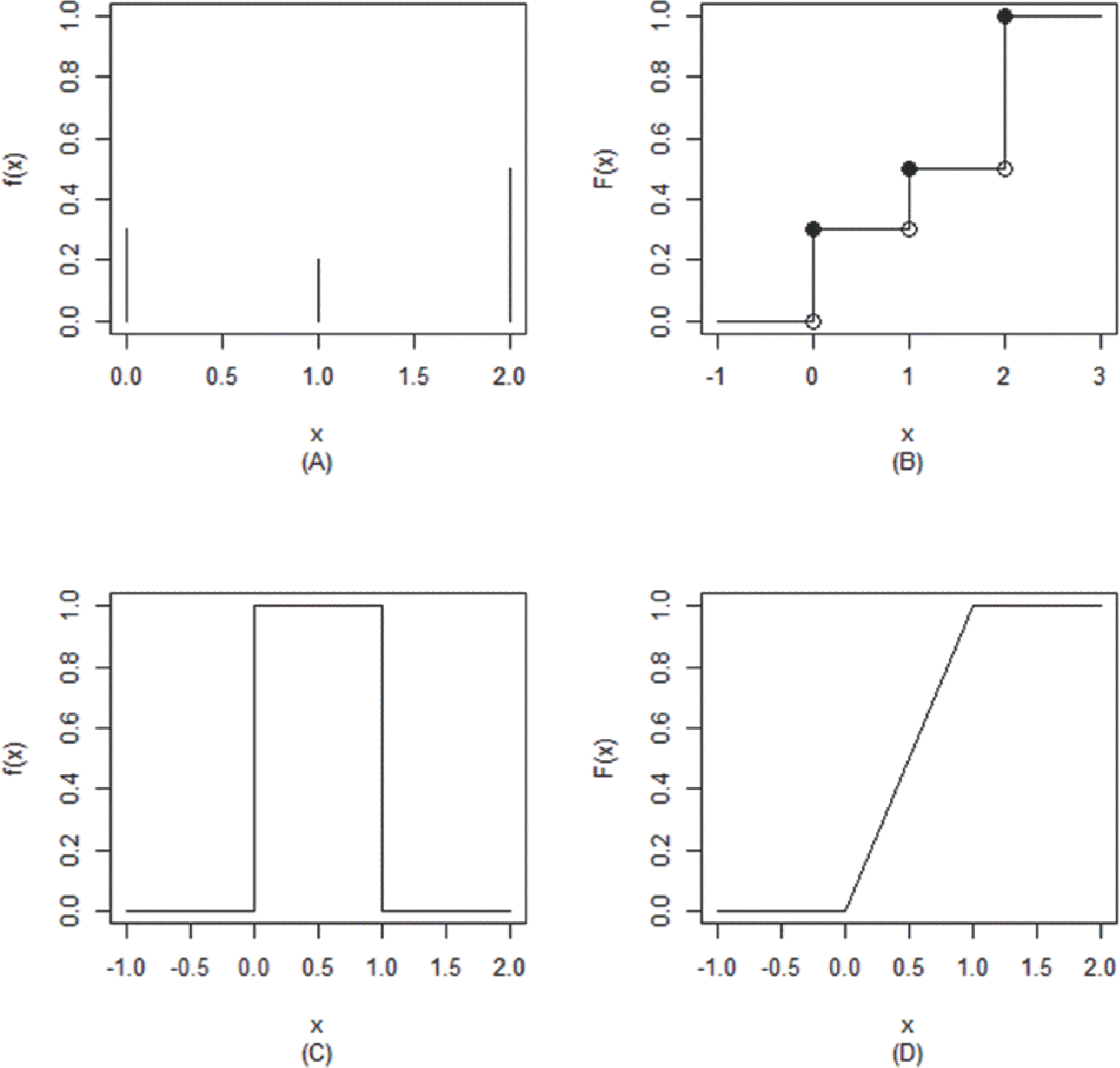
For pharmacometricians, probability theory is the very first obstacle towards the statistics since it is solely founded on mathematics. The purpose of this tutorial is to provide a simple version of introduction to a univariate random variable, its mean, variance, and the correlation coefficient of two random variables using as simple mathematics as possible. The definitions and theorems in this tutorial appear in most of the statistics books in common. Most examples are small and free of subjects like coins, dice, and binary signals so that the readers can intuitively understand them.

Keywords: Probability, Expected values, Moment generating function, Correlation coefficient

References

1. Hogg RV, Craig AT. Introductin to Mathematical Statistics. 4th ed.Macmillan, Publishing Company;1978.
2. Hogg RV, Tanis EA. Probability and Statistical Inference. 3rd ed.Macmillan, Publishing Company;1983.
3. Kim WC, et al. Introduction to Statistics. 4th ed.Youngchi, Seoul;2005.
4. Mood AM, Graybill FA, Boes DC. Introduction to the Theory of Statistics, McGraw-Hill, New York. 1974.
5. Peebles PZ JR. Probability, Random Variables, and Random Signal Principles. 4th ed.McGraw-Hill Korea;2001.
6. Rice JA. Mathematical Statistics and Data Analysis. 3rd ed.Brooks/Cole Cengage Learning;2007.
7. Rosner B. Fundamentals of Biostatistics, 6th ed. 2006.
8. Ross S. A First Course in Probability and Statistical Inference. 8th ed.Pearson Education, New Jersey;2010.

Figure 1.
The probability density function of the population and the histogram of sample.
tcp-24-66f1.tif
Figure 2.
The three routers in a communication system.
tcp-24-66f2.tif
Figure 3.
(A) the pdf of Example 9 (B) cdf of Example 9 (C) the pdf of Example 10 (D) the cdf of Example 10.
tcp-24-66f3.tif
TOOLS
Similar articles