This article has been corrected. See "Erratum: R-based reproduction of the estimation process hidden behind NONMEM Part 2: First-order conditional estimation" in Volume 26 on page 99.
Abstract
The first-order conditional estimation (FOCE) method is more complex than the first-order (FO) approximation method because it estimates the empirical Bayes estimate (EBE) for each iteration. By contrast, it is a further approximation of the Laplacian (LAPL) method, which uses second-order expansion terms. FOCE without INTERACTION can only be used for an additive error model, while FOCE with INTERACTION (FOCEI) can be used for any error model. The formula for FOCE without INTERACTION can be derived directly from the extension of the FO method, while the FOCE with INTERACTION method is a slight simplification of the LAPL method. Detailed formulas and R scripts are presented here for the reproduction of objective function values by NONMEM.
Go to : 
REFERENCES
1.Kang D., Bae KS., Houk BE., Savic RM., Karlsson MO. Standard Error of Empirical Bayes Estimate in NONMEM® VI. Korean J Physiol Pharmacol. 2012. 16:97–106. DOI: doi: 10.4196/kjpp.2012.16.2.97.

2.Sheiner LB., Beal SL. Evaluation of methods for estimating population pharmacokinetics parameters. I. Michaelis-Menten model: routine clinical pharmacokinetic data. J Pharmacokinet Biopharm. 1980. 8:553–571.
3.Sheiner LB., Beal SL. Evaluation of methods for estimating population pharmacokinetic parameters. II. Biexponential model and experimental pharmacokinetic data. J Pharmacokinet Biopharm. 1981. 9:635–651.

4.Sheiner LB., Beal SL. Evaluation of methods for estimating population pharmacokinetic parameters. III. Monoexponential model: routine clinical pharmacokinetic data. J Pharmacokinet Biopharm. 1983. 11:303–319.

5.Kim MG., Yim DS., Bae KS. R-based reproduction of the estimation process hidden behind NONMEM® Part 1: first-order approximation method. Transl Clin Pharmacol. 2015. 23:1–7. DOI: doi: 10.12793/tcp.2015.23.1.1.

6.Beal SL., Sheiner LB., Boeckmann AJ., Bauer R. NONMEM user's guides. Ellicott city, MD, USA. 1989–2011.
7.Wang Y. Derivation of various NONMEM estimation methods. J Pharmacokinet Pharmacodyn. 2007. 34:575–593. DOI: doi: 10.1007/s10928-007-9060-6.

9.Plan EL., Maloney A., Mentre F., Karlsson MO., Bertrand J.Performance com-parison of various maximum likelihood nonlinear mixed-effects estimation methods for dose-response models. AAPS J. 2012. 14:420–432. DOI: doi: 10.1208/s12248-012-9349-2.

10.Peck CC., Beal SL., Sheiner LB., Nichols AI. Extended least squares nonlinear regression: a possible solution to the "choice of weights" problem in analysis of individual pharmacokinetic data. J Pharmacokinet Biopharm. 1984. 12:545–558.

11.Sheiner LB., Beal SL. Pharmacokinetic parameter estimates from several least squares procedures: superiority of extended least squares. J Pharmaco-kinet Biopharm. 1985. 13:185–201.

12.Peck CC., Sheiner LB., Nichols AI. The problem of choosing weights in nonlinear regression analysis of pharmacokinetic data. Drug Metab Rev. 1984. 15:133–148. DOI: doi: 10.3109/03602538409015060.

Go to : 




 PDF
PDF ePub
ePub Citation
Citation Print
Print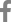




 XML Download
XML Download