Abstract
A fundamental problem in analyzing complex multilevel-structured periodontal data is the violation of independency among the observations, which is an assumption in traditional statistical models (e.g., analysis of variance and ordinary least squares regression). In many cases, aggregation (i.e., mean or sum scores) has been employed to overcome this problem. However, the aggregation approach still exhibits certain limitations, such as a loss of power and detailed information, no cross-level relationship analysis, and the potential for creating an ecological fallacy. In order to handle multilevel-structured data appropriately, mixed effects models have been introduced and employed in dental research using periodontal data. The use of mixed effects models might account for the potential bias due to the violation of the independency assumption as well as provide accurate estimates.
Generally, most of the data collected in dental research contain information on complex inherent structures. In order to assess an individual's oral health status, a dentist must inspect the specific status of each tooth and its adjacent tissue unit. Because a person has multiple teeth and each tooth has multiple surfaces or sites, the resulting data innately contains a large volume of information on these complex structures [1,2,3]. This kind of multilevel-structured data is commonly observed in various dental research fields such as restorative dentistry [4], orthodontics [5], or periodontics [2]. An example of the complex multilevel structure of periodontal data is shown in Fig. 1, which depicts a four-level structure containing time points (level 1), sites (level 2), teeth (level 3), and persons (level 4). Analysis of this complex multilevel-structured data has been challenging because many methodological problems need to be considered and resolved [6,7].
An important problem when analyzing multilevel-structured data is the inherent violation of the independency assumption on which many traditional statistical methods are based. Teeth of a particular person share a common environment within the same oral cavity; therefore, the health status of these teeth may be related to each other. In disaggregation, individuals within a given dataset are approached as independent observations. If the data has a multilevel structure, it is ignored. In this case, a traditional statistical model will be incorrectly applied to a multilevel-structured dataset. One example of this kind of error would be applying the traditional analysis of variance model to correlate the relationship of multiple observations such as the correlation of multiple implants from the same patient. From a practical perspective, collecting information on 100 implants from 40 patients might require less effort and time than examining 100 implants from 100 patients would (assuming that each implant was randomly selected from each patient who might also have multiple implants). The amount of information collected from the 100 implants in 40 patients (correlated data) will likely be smaller than that from 100 implants in 100 patients (independent data). Therefore, if all other conditions are equal, the standard errors calculated from the correlated data will be larger than those from the independent data will be. In other words, if the correlated data is analyzed using the standard analytic methods that assume independence among individuals, a critical problem of underestimating the standard errors may lead to erroneously significant results.
In other cases, multilevel-structured dental data has frequently been treated as an aggregated form of averaged or summed scores. In the field of periodontal research, the gingival index or periodontal index is computed as a mean score of multiple teeth and/or multiple sites. In addition, the degree of dental caries can be operationalized by the decayed, missing, and filled teeth (DMFT) index, which is the sum of the total number of decayed, missing, and filled teeth. However, this aggregation method has demonstrated at least three shortcomings. First, a substantial loss of power is inevitable because a small number of aggregated values are used in the data analysis. For instance, each patient has only one DMFT value in the data analysis, instead of all of their observed records on dental caries experienced in all of their teeth. Second, there might be a loss of detailed observations. For example, a small number of deep pockets or a large number of shallow pockets can give the same averaged or summed periodontal index score, even though these data were obtained from very different measures status. Similarly, a high DMFT index score may imply that either the patient has many decayed teeth or many treated, filled teeth, which are quite different conditions from the viewpoint of treatment requirements. Third, it is impossible to estimate the status or the change in any conditions at the lower level such as at the teeth level. For example, evaluating the effectiveness of a periodontal treatment based on a specific change to the periodontal status around a tooth is impossible when only an aggregated score per subject is provided.
There are two general classes of approaches for analyzing data with a complex multilevel structure: the multilevel mixed effects model [8,9,10] and the generalized estimating equation (GEE) approach [11]. A noteworthy difference between these two methods is whether the differences between persons have been explicitly modeled or not. A characteristic of correlated, multilevel-structured data is the existence of heterogeneity between higher level units (i.e., a difference between average values or average effects among certain groups/persons). While the multilevel mixed effects model explicitly analyses the higher unit-specific differences, the GEE method accounts for these differences implicitly by regarding them as an unwanted interference. These two classes of models can be generalized to create models for continuous, binary, ordered, or counted outcomes.
To illustrate the main differences between these two classes of models, models for binary outcomes are exemplified below. The simplest form of a multilevel mixed effects model for a binary outcome can be obtained by introducing a random intercept, bj, which represents the difference between higher level units (e.g., with the tooth as the first level and the person as the second level). The simplest multilevel mixed effects model is:
where, Yij is the outcome variable for jth individual's ith tooth, β0j is the intercept for jth individual, β1j is the slope for jth individual, and Xij is the predictor for jth individual's ith tooth. According to the types of outcome variables, a link function (e.g., identity, log, or logit) can be used. In addition, various error covariance structures such as homogeneous, heterogeneous, or autocorrelated structures among residuals can be explicitly modeled to account for the error at the teeth level. Thus, the equation models the relation between the predictors and outcomes at the second level. The mixed effect models might represent associations between predictors and the binary outcome variable at the person level as well as at the teeth level. Specifically, the intercept and the effects of the predictors on the outcome variable at the teeth level are assumed to vary across the individual in a population [12,13]. The models at the second level can be expressed as:
where, γ00 and γ10 are the average intercept and slope at the population level, respectively. Generally, the covariance structure among deviation scores at the person level is assumed to be normally distributed. Those coefficients are referred to as fixed effects, which are interpreted as the population values. Additionally, u0j and u1j are the deviation scores from the average scores at the individual level. Those coefficients are referred to as random effects that explicitly indicate the degree to which the intercept and slopes vary among persons. Because the two effects are combined in the single equation and model, the model is referred to as the mixed effects model. Finally, the magnitude of the design effects (i.e., the violation of independence among these teeth) could be estimated by intraclass correlation. Intraclass correlation is the percentage of observed variation in the outcome variable attributable to person-level characteristics. This percentage could be computed in an unconditional model.
On the other hand, the GEE approach for a binary outcome can be expressed as the following model:
where Yij is the outcome variable for jth individual's ith tooth, β0* is the average intercept at the person level, β1* is the average slope at the person level, and Xij is the predictor for jth individual's ith tooth. Additionally, link functions are selected depending on the type of outcome variable. The regression parameters in the GEE model represent population-averaged effects, and the GEE models the correlations or covariances among the teeth to account for the correlations evident between lower level units that exist within higher level units [12,14]. Researchers who employ the GEE are typically interested in estimating the effects of predictors on outcome variables at the person level. Because the interest is at the person level, the covariance structures at the teeth level such as repeated or clustered observations could be reasonably modeled to estimate regression coefficients and the corresponding standard errors. Deciding between these two models to analyze correlated (repeated or clustered) data may mainly depend on whether the effect of higher level units or population-averaged effects are of interest.
Three noteworthy examples of periodontal research that applied the multilevel mixed effects model are introduced in Table 1. Tu et al. [15,16] investigated the longitudinal relationships between the outcomes lifetime cumulative attachment loss (LCAL) and probing depth in relation to potential risk factors for periodontal disease progression. The risk factors of interest included site-level factors (supragingival calculus, subgingival calculus, and bleeding on probing), tooth-level factors (tooth position), and subject-level factors (number of sites with a LCAL>1 mm and smoking status). The multilevel mixed effects model was applied, and the results revealed a linear relationship for tooth position and a significant effect for subgingival calculus and bleeding on probing with both LCAL and probing depth. Pereira et al. [17] explored the association between plasmic human immunodeficiency virus viral load and subgingival microbiota measured at 12 sites in each patient with chronic periodontitis (six sites from a tooth with the highest probing depth and six with a tooth in good periodontal health). A two-level model for an ordinal outcome variable was constructed with sites as the first level and persons as the second level. Last, Guglielmetti et al. [18] aimed to compare the presence and number of periodontal pathogens in smokers and never-smokers. Using four subgingival plaque samples collected from each person, the presence and number of bacteria were analyzed using the multilevel mixed model logistic regression and multilevel mixed model linear regression, respectively.
Abuhussein et al. [19] investigated factors associated with apoptosis in serum, saliva, and gingival crevicular fluid (GCF) and their associations with periodontal disease severity and activity. Clinical assessments such as those testing for gingivitis, measuring the number of deep pockets, and categorizing patients into mild or moderate/severe chronic periodontitis groups were determined at six sites per tooth. In addition, the GCF sample was collected from the mesiobuccal site of each tooth. To adjust for the correlated multiple measures taken from each patient, the GEE was implemented. The outcomes of interest were the aforementioned clinical groups and the number of deep pockets. The main explanatory variables were the level of GCF DNA fragmentation and presence or absence of the apoptosis markers. In patients with chronic periodontitis, factors associated with apoptosis in GCF were reported after adjustment for the multiple observations (in the mesio-buccal site of each tooth) that were performed in each patient.
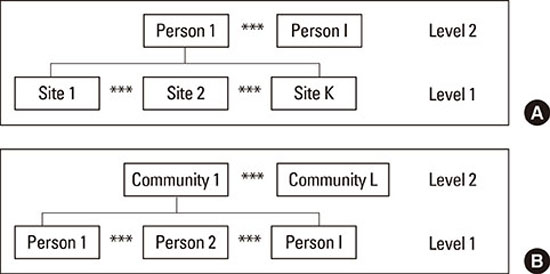
Fig. 2 depicts the collection framework for a multilevel-structured dataset with multiple repeated measurements taken at the person or community level. Table 2 lists specific examples of these kinds of data in periodontal research. Multiple repeated measures in the same individual are frequently used in an attempt to measure the variable accurately. For example, Monje et al. [20] measured the sinus lateral wall thickness in atrophic posterior maxillae at six different sites in each patient; therefore, multiple repeated observations were made at the person level (Fig. 2A). Because correlated repeated measures were made in the same person, a mixed effects model was applied to assess the effects of residual ridge height, sex, and age on sinus lateral wall thickness. After consideration of the repeated measurements, the authors found that sinus lateral wall thickness was influenced by residual ridge height, the presence of teeth, and age.
The multilevel structure is a general phenomenon in data obtained from society, which also has a natural, multilevel structure. Many aspects of the human society frequently form a multilevel structure, (e.g., the four-level structure of students (level 1), classes (level 2), schools (level 3), and districts (level 4). Vettore et al. [21] investigated the prevalence and geographical distribution of periodontal disease and its association with contextual and individual social inequalities. Contextual effects mean that a higher level (community level in the example) factor affects the relationship with the lower level (person level) factor and the outcome variables. In their study, social inequalities were assessed using the Human Development Index and the Gini Index of Income Inequality. A multilevel model was implemented to accommodate the multilevel structure of the data and evaluate the contextual relationship of periodontal disease state (person-level variable) with the second-level variables. The authors concluded that income inequality (the second-level, community variable) plays a significant role in the occurrence of severe periodontal disease (the first-level, personal variable).
A fundamental problem in analyzing complex multilevel-structured periodontal data is the violation of independency among the observations. In order to handle multilevel-structured data appropriately, the mixed effects models should be used. In doing so, the bias resulting from the violation of the independency assumption might be avoided and the estimates might be provided accurately.
Figures and Tables
Figure 2
Depiction of repeated measurements (A) at multiple sites in a single individual (person level) and (B) in multiple individuals in a community (community level).
Table 1
Examples of published periodontal studies using multilevel mixed effects modeling.

| Source | Feature | Contents |
|---|---|---|
| Tu et al. (2004) [15] | Purpose | To investigate longitudinal relationships between the outcomes of lifetime cumulative attachment loss and probing depth in relation to potential risk factors for periodontal disease progression |
| Outcome variable | Lifetime cumulative attachment loss and probing depth | |
| Covariates | Site level (supragingival calculus, bleeding on probing, etc.), tooth level (tooth position), subject level (smoking status etc.) | |
| Measurements | From 1986 to 1989 at baseline, 12 months, and 30 months; all the teeth; mesio-buccal, disto-buccal, disto-lingual, and mesio-lingual surfaces of all teeth | |
| Statistical analysis | Multilevel modeling | |
| Pereira et al. (2014) [17] | Purpose | To investigate the association between detectable plasmatic human immunodeficiency virus (HIV) viral load and high levels of periodontal- and non-periodontal-related microorganisms in the subgingival microbiota of individuals with HIV. |
| Outcome variable | Ordered variable of 35 bacterial species (0, not detected; 1, low levels; 2, mild levels; 3, high levels) | |
| Measurements | At 12 sites of each individual with chronic periodontitis (six sites of the tooth with highest pocket depth and six sites of the tooth with periodntal health - disto-buccal, buccal, mesio-buccal, disto-lingual, lingual, and mesio-lingual) | |
| Statistical analysis | Multilevel ordinal regression (two-level random-intercepts and fixed slopes model considering periodontal sites nested within individuals) | |
| Guglielmetti et al. (2014) [18] | Purpose | To compare the presence and number of periodontal pathogens in smokers and never-smokers |
| Outcome variable | Presence and mean number of bacteria | |
| Measurements | Four measurements from each patient (a pooled subgingival plaque sample from the deepest periodontal pocket in each quadrant) | |
| Statistical analysis | Multilevel mixed logistic regression for presence of bacteria; multilevel mixed-model linear regression for the mean number of bacteria |
Table 2
Published periodontal studies analyzing data with repeated sites and repeated time points.

| Source | Feature | Contents |
|---|---|---|
| Monje et al. (2014) [20] | Purpose | To examine the sinus lateral wall thickness of atrophic posterior maxilla |
| Outcome variable | Residual ridge height (RH, the distance from the alveolar crest up to the lowest points of the sinus floor) and lateral wall thickness (LWT, a perpendicular line at 3, 5, 7, 10, 13, and 15 mm from the lowest point of the sinus floor) | |
| Measurements | Six LWTs and one RH in millimeters from a maxillary sinus | |
| Statistical analysis | The mixed linear model was used to test the effect of sex, type of edentulism, etc., on LWT of the sinus | |
| Vettore et al. (2013) [21] | Purpose | To estimate the prevalence and geographical distribution of periodontal disease and its association with contextual and individual social inequalities |
| Outcome variable | Severity of periodontal disease (moderate, severe) using the community periodontal index and clinical attachment loss | |
| Explanatory variable | Contextual characteristics of cities - human development index, gini index | |
| Measurements | Cross-sectional | |
| Statistical analysis | Multilevel logistic regression |
References
1. Gilthorpe MS, Griffiths GS, Maddick IH, Zamzuri AT. An application of multilevel modelling to longitudinal periodontal research data. Community Dent Health. 2001; 18:79–86.
2. Gilthorpe MS, Griffiths GS, Maddick IH, Zamzuri AT. The application of multilevel modelling to periodontal research data. Community Dent Health. 2000; 17:227–235.
3. Gilthorpe MS, Maddick IH, Petrie A. Introduction to multilevel modelling in dental research. Community Dent Health. 2000; 17:222–226.
4. Gilthorpe MS, Mayhew MT, Bulman JS. Multilevel survival analysis of amalgam restorations amongst RAF personnel. Community Dent Health. 2002; 19:3–11.
5. Gilthorpe MS, Cunningham SJ. The application of multilevel, multivariate modelling to orthodontic research data. Community Dent Health. 2000; 17:236–242.
6. Hannigan A, Lynch CD. Statistical methodology in oral and dental research: pitfalls and recommendations. J Dent. 2013; 41:385–392.

7. Macfarlane TV, Worthington HV. Some aspects of data analysis in dentistry. Community Dent Health. 1999; 16:216–219.
9. Mason WM, Wong GM, Entwistle B. Contextual analysis through the multilevel linear model. In : Leinhardt S, editor. Sociological methodology. San Francisco: Jossey-Bass;1983. p. 72–103.
10. Bolker BM, Brooks ME, Clark CJ, Geange SW, Poulsen JR, Stevens MH, et al. Generalized linear mixed models: a practical guide for ecology and evolution. Trends Ecol Evol. 2009; 24:127–135.

11. Liang KY, Zeger SL. Longitudinal data analysis using generalized linear models. Biometrika. 1986; 73:13–22.

12. Kim HY, Preisser JS, Rozier RG, Valiyaparambil JV. Multilevel analysis of group-randomized trials with binary outcomes. Community Dent Oral Epidemiol. 2006; 34:241–251.

13. Diez Roux AV. A glossary for multilevel analysis. J Epidemiol Community Health. 2002; 56:588–594.

14. Hu FB, Goldberg J, Hedeker D, Flay BR, Pentz MA. Comparison of population-averaged and subject-specific approaches for analyzing repeated binary outcomes. Am J Epidemiol. 1998; 147:694–703.

15. Tu YK, Gilthorpe MS, Griffiths GS, Maddick IH, Eaton KA, Johnson NW. The application of multilevel modeling in the analysis of longitudinal periodontal data--part I: absolute levels of disease. J Periodontol. 2004; 75:127–136.

16. Tu YK, Gilthorpe MS, Griffiths GS, Maddick IH, Eaton KA, Johnson NW. The application of multilevel modeling in the analysis of longitudinal periodontal data--part II: changes in disease levels over time. J Periodontol. 2004; 75:137–145.

17. Pereira VT, Pavan P, Souza RC, Souto R, Vettore MV, Torres SR, et al. The association between detectable plasmatic human immunodeficiency virus (HIV) viral load and different subgingival microorganisms in Brazilian adults with HIV: a multilevel analysis. J Periodontol. 2014; 85:697–705.

18. Guglielmetti MR, Rosa EF, Lourencao DS, Inoue G, Gomes EF, De Micheli G, et al. Detection and quantification of periodontal pathogens in smokers and never-smokers with chronic periodontitis by real-time polymerase chain reaction. J Periodontol. 2014; 85:1450–1457.

19. Abuhussein H, Bashutski JD, Dabiri D, Halubai S, Layher M, Klausner C, et al. The role of factors associated with apoptosis in assessing periodontal disease status. J Periodontol. 2014; 85:1086–1095.

20. Monje A, Catena A, Monje F, Gonzalez-García R, Galindo-Moreno P, Suarez F, et al. Maxillary sinus lateral wall thickness and morphologic patterns in the atrophic posterior maxilla. J Periodontol. 2014; 85:676–682.

21. Vettore MV, Marques RA, Peres MA. Social inequalities and periodontal disease: multilevel approach in SBBrasil 2010 survey. Rev Saude Publica. 2013; 47:Suppl 3. 29–39.




 PDF
PDF ePub
ePub Citation
Citation Print
Print




 XML Download
XML Download