Abstract
Objective
The purpose of this study was to determine whether the results of fractal analysis can be used as criteria for midpalatal suture maturation evaluation.
Methods
The study included 131 subjects aged over 18 years of age (range 18.1–53.4 years) who underwent cone-beam computed tomography. Skeletonized images of the midpalatal suture were obtained via image processing software and used to calculate fractal dimensions. Correlations between maturation stage and fractal dimensions were calculated using Spearman's correlation coefficient. Optimal fractal dimension cut-off values were determined using a receiver operating characteristic curve.
Results
The distribution of maturation stages of the midpalatal suture according to the cervical vertebrae maturation index was highly variable, and there was a strong negative correlation between maturation stage and fractal dimension (−0.623, p < 0.001). Fractal dimension was a statistically significant indicator of dichotomous results with regard to maturation stage (area under curve = 0.794, p < 0.001). A test in which fractal dimension was used to predict the resulting variable that splits maturation stages into ABC and D or E yielded an optimal fractal dimension cut-off value of 1.0235.
Orthopedic expansion of the palate was first described approximately 150 years ago in a case review by Angell.1 It has also been reported that in growing children, expansion of maxillary width can improve posterior cross bite, increase nasal width, reduce nasal resistance, and improve breathing.2 However, there are many potential pitfalls associated with rapid maxillary expansion (RME) treatment in adults, due to closure of the midpalatal suture and the strong buttress of the sphenoid, zygomatic, and nasal bones and the nearby structures.3 Owing to these factors, RME treatment in adults can induce bending of the alveolar bone, compression of the periodontal ligament, resorption of the buccal root, perforation of the buccal alveolar bone, severe pain, periodontal side effects, and gingival recession of the maxillary molar area.4 Therefore, when non-surgical expansion of the midpalatal suture is deemed impossible in an adult, RME can be performed by surgical means via osteotomy of the midpalatal suture and corticotomy of the nearby skeletal structure.
In adults, surgically assisted rapid maxillary expansion (SARME) has advantages such as improved nasal breathing, aesthetic enhancement due to reduction of the buccal corridor, and reducing the potential need for extraction treatment.5 However, it is also reportedly associated with disadvantages including pressure-related non-infectious frank necrosis (in approximately 1.8% of cases),6 bleeding and infection during surgery, joint pain, periodontal problems, recurrence,7 and a requirement for surgery with hospitalization. Another limitation of SARME is that it generally cannot be performed when the discrepancy in width requires an improvement of more than 7 mm.8
Currently, if the midpalatal suture has already closed in an adult, the only method of resolving the discrepancy in width is SARME. However, if the degree of closure of the midpalatal suture can be accurately determined, the traditional RME method may be used for expansion of the palate, even in aged patients. In general, the midpalatal suture is known to start closing at the ages of 14–15 years in female subjects and 15–16 years in male subjects,9 and thereafter closure of the midpalatal suture increases until the age of approximately 30 years in both sexes. However, the timing and degree of maturation vary substantially between individuals, and closure usually begins posteriorly and progresses anteriorly.10 The rate of ossification throughout the suture area is slow in all individuals, and the highest ossification rate in the older age group was reportedly only 13.1% with a 44-year-old male subject.11 A recent quantitative study based on micro-computed tomography (micro-CT) suggests that the degree of ossification or maturation of the midpalatal suture may be extremely low, and that the degree of interdigitation is independent of age.12
Most reports on the degree of closure of the midpalatal suture published to date are histological micro-CT studies based on autopsies,13 but the methods used in these studies cannot be clinically applied to patients for diagnostic purposes. A recently developed method involving descriptive evaluation of the midpalatal suture via cone-beam computed tomography (CBCT) imaging has been proposed,14 but that method entails potential variability among observers with regard to selecting the regions of interest (ROIs), and the quality of the images utilized. Therefore, it is necessary to develop a CBCTbased method incorporating more objectively selected ROIs, in order to determine the degree of closure of the midpalatal suture.15
Studies of the shape of human cranial sutures suggest that a suture can be seen as a fractal pattern with high confidence.16 "Fractal", a term first used by Kauffman17 in the 1970s, includes the concepts "break" and "fragment". The first fractal analysis of cranial suture in mammals was conducted in the 1980s.18 Subsequent studies incorporating fractal analysis showed that fractal dimensions are proportional to localized stress,19 and that more complex suture forms are associated with a smaller distance between the two relevant bones.20 However, there have been no fractal studies on sutures other than those investigating cranial sutures, and a distinct lack of fractal studies using CBCT have been reported.
The purpose of this study was to evaluate the correlation between fractal dimension and maturation of the midpalatal suture with CBCT data, and to determine whether the results of fractal analysis may be used as criteria to determine maturation stage in a clinical setting.
A selection of adult patients hospitalized at the orthodontics department at Pusan National University Dental Hospital in 2013 (144 in total, 72 men and 72 women) who underwent CBCT imaging (Zenith 3D; Vatech Co., Gyeonggi-do, Korea) for diagnostic purposes were enrolled in the study. Thirteen patients breached the inclusion criteria (lesions, incisive canal cysts or impacted teeth; congenital bone defects, cleft palate; sinus pneumatization in the midpalatal area), resulting in a final subject pool of 131 patients (69 men and 62 women) with a mean age of 24.1 ± 5.9 years (male subjects 23.1 ± 5.8 years, female subjects 25.2 ± 5.9 years) and an age range of 18.1–53.4 years. The cervical vertebrae maturation (CVM) index distribution of the patients is shown in Table 1. This study was approved by the institutional review board of Pusan National University Dental Hospital (PNUDH-2014-018).
While undergoing CBCT, the patients stood in line with the Frankfort horizontal plane, parallel to the ground surface and in the maximum intercuspal position. The CBCT settings used were: field of view 20 × 19 cm; tube voltage 90 kVp; tube current 4.0 mA; scan time 24 s). Using a CT analysis program (Ez3D 2009; Vatech Co.), antero-posterior reference lines on the axial plane were set to pass at the midpalatal suture, and a horizontal reference line on the coronal plane was set to coincide with the line connecting the center of the palate in the maxillary first molar area. A panoramic curve was then configured for the antero-posterior connection on the sagittal plane crossing the midpalatal suture. Thickness was set to 0 mm to avoid surrounding structures (i.e., the vomer) being mistaken for a radiopaque region of the midpalatal suture. A curve was then defined to connect the vertical center of the bone constituting the midpalatal part (Figure 1). All CBCT images were taken under the same voltage and current conditions without adjustment of the contrast or brightness, and then captured under the same conditions (window level, 1,298 HU; width, 4,498 HU).
The maturation classification system suggested by Angelieri et al.14 was used, whereby 5 different types of midpalatal sutural morphology are distinguished based on intermaxillary bony line shapes. An example of the images classified is shown in Figure 1D. Each image was classified into stages A–E. These descriptive stages of midpalatal suture maturation determined via standardized CBCT cross-sectional images in the axial plane were as follows: A, straight sutural line with little or no interdigitation; B, scalloped high-density midpalatal suture line; C, two parallel, scalloped, high-density midpalatal suture lines close to each other; D, invisible suture line in palatine bone; and E, actual suture is not visible in at least a portion of the maxilla. The principal examiner, who was well trained in this method, classified all images. This evaluation was considered 'ground truth' rather than 'gold standard'. Two days later, the same examiner reclassified 30 randomly selected images to evaluate intra-examiner reliability. To evaluate inter-examiner reliability, two other experienced orthodontists (each with over 1 year of experience in interpreting CBCT scans for diagnostic purposes) classified 30 randomly selected images under the same conditions (same room lighting and computer monitor).
ROIs were selected from images similar to that shown in Figure 1D by cropping them. The cortical lining part of the incisive canal was excluded from the ROI because it increases the radiopaque region, which may affect the calculation of fractal dimension. A narrow ROI was set forth from the rear of the incisive canal to the front of the posterior nasal spine to exclude parts other than the midpalatal suture. An image-processing program (Photoshop CS6 Extended; Adobe Systems, San Jose, CA, USA) was used to process the images in accordance with the method devised by White and Rudolph,21 as follows: A Gaussian filter (sigma = 35 pixels) was applied to each ROI to remove structures with small or intermediate sizes and blurring was performed until only structures with large differences in density remained. This blurred image was subtracted from the original image. Image J version 1.48 software (National Institute of Health, Bethesda, MD, USA) was then used to create a binary image. Erosion and dilation were performed once to reduce noise, and the image was skeletonized. Fractal dimension was then obtained via the box-counting function of Image J (Figure 2).
A weighted kappa coefficient was calculated to evaluate inter- and intra-examiner reliability using MedCalc version 12.3.0 (MedCalc Software, Oostende, Belgium). Agreement was defined in accordance with the scale described by Landis and Koch22 (< 0, no agreement; 0–0.20, slight agreement; 0.21–0.40, fair agreement; 0.41–0.60, moderate agreement; 0.61−0.80, substantial agreement; 0.81–1.00, almost perfect agreement). All data are presented as mean ± standard deviation values. A Scheffe's ANOVA test was performed to compare fractal dimension at each maturation stage. The correlation between maturation stage and fractal dimension was estimated using Spearman's correlation coefficient. The optimal cut-off value of fractal dimension was estimated by using a receiver operating characteristic (ROC) curve. IBM SPSS Statistics version 21.0 software (IBM Co., Armonk, NY, USA) was used for all statistical analyses, and p < 0.05 was considered statistically significant.
The intra-examiner reliability analysis showed almost perfect agreement for fractal dimension, with a weighted kappa coefficient of 0.84 (95% confidence interval [CI] 0.74–0.93). The inter-examiner reliability analysis showed substantial agreement for fractal dimension, with weighted kappa coefficients from 0.67 (95% CI 0.38–0.95) to 0.72 (95% CI 0.48–0.97). With regard to the CVM index, the inter-examiner reliability analysis demonstrated substantial agreement, with weighted kappa coefficients from 0.69 (95% CI 0.53–0.86), and the intra-examiner reliability demonstrated substantial agreement, with weighted kappa coefficients from 0.71 (95% CI 0.56−0.86).
The distribution of maturation stages of the midpalatal suture according to the CVM index was variable (Table 2). There were no subjects with CVM I–IV or maturation stage A. Among the 21 subjects with CVM V, maturation stages B–C, in which the midpalatal suture is not fused, were found in 13 (61.9%; males 77.8%, females 50.0%). Among the 110 subjects with CVM VI, maturation stages B–C were found in 42 (38.2%; males 41.6%, females 34.0%). In total, maturation stages B–C were found in 55 of the 131 subjects (41.9%; males 32/69, 46.4%; females 23/62, 37.1%). The Scheffe's post-hoc analysis shown in Table 2 was performed using total subjects, due to the limited numbers of patients classified as CVM V and CVM VI. There were differences in mean fractal dimension between maturation stages B, C, D, and E.
A strong negative correlation was found between maturation stage and fractal dimension (−0.623, p < 0.001; Table 3, Figure 3). The correlation coefficients for males and females were −0.649 (p < 0.001) and −0.569 (p < 0.001) respectively.
A ROC curve (Figure 4) was used to express the boundary between maturation stages A–C and D or E, for which fusion of the midpalatal suture could be determined as a fractal dimension. Fractal dimension was found to be a statistically significant indicator that predicted dichotomous maturation stage results (area under curve [AUC] = 0.794, p < 0.0001). At the optimal fractal dimension cut-off value of 1.0235, a test in which fractal dimension was used to predict the variable that splits maturation stages into A–C and D or E resulted in the following values: Sensitivity 64.9%, specificity 86.6%, false positive rate 35.1%, false negative rate 13.4%, positive predictability 80.3%, and negative predictability 74.6%.
The appropriate time for maxillary expansion has been a matter of great controversy. Some authors have suggested that surgery should be considered for patients older than 14 years,23 whereas others have argued that surgery should only be considered for male patients older than 25 years and female patients older than 20 years.24 Similarly, there are contrasting views on the timing of fusion of the midpalatal suture. In our study, the distribution of maturation stages indicated that the midpalatal suture remained in a non-fused state in a large proportion of adults. This implies that age should not be the only factor used to determine whether SARME can be performed, and that conventional RME may be possible in adults. Indeed, in some studies RME has been performed in adults.2425
The availability of a method to accurately evaluate the midpalatal suture would facilitate the avoidance of errors associated with uniformly using SARME according to age. Currently, the objective indicators to determine maturation stage are unclear. The CBCT-based method proposed by Angelieri et al.14 is a useful and simple method that may prove valuable for clinical application. In our study, the reliability of this method was sufficiently high to justify its use in clinics. However, examiners required a lot of training to reach an adequate level of proficiency. Therefore, we evaluated whether a more objective and quantitative method incorporating fractal analysis could provide diagnostic criteria. As a strong negative correlation between fractal dimension and maturation stage was established in our study using fractal analysis, it may be a viable alternative to the method suggested by Angelieri et al.14 Fractal analysis has the advantage of being more objective and quantitative than other methods. Our study used a panoramic curve to obtain the image of the midpalatal suture area, which can be easily applied to different palatal planes.
The study by Angelieri et al.14 divided maturation stage dichotomously into A–C and D or E. These authors suggested that this delineation represented the boundary between the viability and non-viability of conventional RME. Like wise, our study aimed to find a fractal dimension value that would classify maturation stage into A–C and D or E, and this was achieved by using a ROC curve (Figure 4). After drawing a curve with the false positive rate (100% specificity) plotted on the x-axis and the true positive rate (sensitivity) plotted on the y-axis, the optimal cut-off value of these two axes with a conflicting relationship (i.e., the value of fractal dimension that maximizes sensitivity and specificity) was found to be 1.0235. In this study, the AUC was 0.794 (p < 0.0001). Since the AUC yielded a high value, it would be reasonable to consider this value the boundary that determines fusion of the midpalatal suture. Obviously, there is a limit to using the absolute cut-off value determined in our study. However, if criteria are provided for a direct comparison of the fractal dimensions of each individual, this value could become an extremely simple and useful clinical indicator for evaluating the possibility of maxillary expansion during the first clinical examination.
Many studies are being conducted using fractal analysis, and its usefulness in dental research has been demonstrated.26 Based on the current study, we suggest that fractal analysis could be used as a method for evaluating the midpalatal suture. However, some problems would need to be solved before it could be used as a diagnostic method in the clinic.
First, according to a study by Lee et al.,27 there is an association between fractal dimension and bone marrow density. In relation to this, Majumdar et al.28 argued that there is value in studying osteoporosis using fractal dimension analysis. In other words, differences in fractal dimension values reflect differences in bone density among individuals, and it can be impractical to directly compare this value between individuals. This notion is supported by the fact that different studies on fractal dimension in the normal maxillary interdental bone29 have yielded different normal values. Similarly, to make the optimal cut-off value that determines fusion of the midpalatal suture meaningful, the accuracy of using fractal dimension in the clinic may be further increased by using the ratio of the fractal dimension value of the midpalatal suture to the value derived from a specific reference point (i.e., specific cranial suture), instead of directly comparing fractal dimension values between individuals.
Second, the methods of determining fractal dimensions are extremely diverse, for example simplified spatial methods (such as the caliper method, tile counting method, and pixel dilation method), general spatial methods (such as the box counting method, intensity variance method, Hurst method, variation method, and blanket method), and spectral methods (such as spatial and spectral methods and the power spectrum method) have all been reported.30 Geraets and van der Stelt30 revealed that fractal dimensions reported in studies using fractal analysis for bone diseases differ according to the methods used. As fractal dimensions can differ according to the calculation methods used, it is necessary to unify the methods used for clinical applications.
Third, errors may accumulate at each of the several steps required to calculate fractal dimensions (from configuration of ROI to image processing), which may influence the final results. In addition to selecting the optimal method to determine fractal dimensions, accuracy may be improved further by devising a means to reduce the number of steps involved in calculating them.
Despite the inevitable problems associated with the clinical application of fractal dimension, a significant association between fractal dimension and the maturation stage of the midpalatal suture was demonstrated in our study. Therefore, as there are not enough objective quantitative indicators to determine the maturation stage of the midpalatal suture in the clinic, our study is meaningful and constitutes a sufficiently useful and valuable method, provided that the problems mentioned above can be addressed. In the future, if it is combined with histologic studies, it can be expected to provide a basis for the development of methods that can be more objectively applied to fractal analysis. If the maturation stage of the midpalatal suture can be determined before maxillary expansion in adults, it would be useful for determining the indications for non-surgical RME.
According to the distribution of maturation stages, the proportion of non-fusion of the midpalatal suture is higher in adults than is currently assumed. Therefore, uniformly performing SARME according to age is not appropriate. Based on the current study, we concluded the following:
1. There is a strong correlation between fractal dimension and the maturation stage of the midpalatal suture.
2. The optimal fractal dimension cut-off value can be determined and utilized as a reference for the use of non-surgical RME.
3. Fractal analysis is an objective and quantitative method; therefore, it may be useful for the evaluation of midpalatal suture maturation.
Figures and Tables
Figure 1
Cone-beam computed tomography (CBCT) imaging. A, Antero-posterior reference lines in the axial plane; the line passing through the midpalatal suture. B, A horizontal reference line in the coronal plane; the line connecting the center of the palate in the maxillary first molar area. C, Generation of a panoramic curve that connects the vertical center points of the palate in the sagittal plane passing through the midpalatal suture. D, Palatal area after generating the panoramic curve. A box indicates the region of interest (ROI). A narrow ROI was established from the rear of the incisive canal to the front of the posterior nasal spine, in order to exclude parts other than the midpalatal suture.
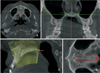
Figure 2
The fractal dimension calculation process. A, Image subtracted from the original image after performing Gaussian blurring of the region of interest. B, Image skeletonized after creating a binary image. C, Fractal dimension calculated via the box counting method.

Figure 4
Receiver operating characteristic curve. When the optimal fractal dimension cut-off value was 1.0235, sensitivity, specificity, false positive rate, false negative rate, positive predictability, and negative predictability were 64.9%, 86.6%, 35.1%, 13.4%, 80.3%, and 74.6% respectively.

Notes
References
1. Angell EH. Treatment of irregularity of the permanent or adult teeth. Dental Cosmos. 1860; 1:540–544.
2. Doruk C, Sökücü O, Sezer H, Canbay EI. Evaluation of nasal airway resistance during rapid maxillary expansion using acoustic rhinometry. Eur J Orthod. 2004; 26:397–401.

3. Baldawa RS, Bhad WA. Stress distribution analysis during an intermaxillary dysjunction: A 3-D FEM study of an adult human skull. Ann Maxillofac Surg. 2011; 1:19–25.

4. Carmen M, Marcella P, Giuseppe C, Roberto A. Periodontal evaluation in patients undergoing maxillary expansion. J Craniofac Surg. 2000; 11:491–494.

5. Koudstaal MJ, Smeets JB, Kleinrensink GJ, Schulten AJ, van der Wal KG. Relapse and stability of surgically assisted rapid maxillary expansion: an anatomic biomechanical study. J Oral Maxillofac Surg. 2009; 67:10–14.

6. Lehman JA Jr, Haas AJ. Surgical-orthodontic correction of transverse maxillary deficiency. Dent Clin North Am. 1990; 34:385–395.
7. Mehra P, Cottrell DA, Caiazzo A, Lincoln R. Life-threatening, delayed epistaxis after surgically assisted rapid palatal expansion: a case report. J Oral Maxillofac Surg. 1999; 57:201–204.

8. Silverstein K, Quinn PD. Surgically-assisted rapid palatal expansion for management of transverse maxillary deficiency. J Oral Maxillofac Surg. 1997; 55:725–727.

9. Korn EL, Baumrind S. Transverse development of the human jaws between the ages of 8.5 and 15.5 years, studied longitudinally with use of implants. J Dent Res. 1990; 69:1298–1306.

10. Persson M, Thilander B. Palatal suture closure in man from 15 to 35 years of age. Am J Orthod. 1977; 72:42–52.

11. Knaup B, Yildizhan F, Wehrbein H. Age-related changes in the midpalatal suture. A histomorphometric study. J Orofac Orthop. 2004; 65:467–474.
12. Korbmacher H, Schilling A, Püschel K, Amling M, Kahl-Nieke B. Age-dependent three-dimensional microcomputed tomography analysis of the human midpalatal suture. J Orofac Orthop. 2007; 68:364–376.

13. Melsen B. Palatal growth studied on human autopsy material. A histologic microradiographic study. Am J Orthod. 1975; 68:42–54.
14. Angelieri F, Cevidanes LH, Franchi L, Gonçalves JR, Benavides E, McNamara JA Jr. Midpalatal suture maturation: classification method for individual assessment before rapid maxillary expansion. Am J Orthod Dentofacial Orthop. 2013; 144:759–769.

15. Tian Y, Liu F, Sun H, Lv P, Cao Y, Yu M, et al. Alveolar bone thickness around maxillary central incisors of different inclination assessed with conebeam computed tomography. Korean J Orthod. 2015; 45:245–252.

16. Yu JC, Wright RL, Williamson MA, Braselton JP 3rd, Abell ML. A fractal analysis of human cranial sutures. Cleft Palate Craniofac J. 2003; 40:409–415.

17. Kauffman SA. Part I. 5. Self organization and adaptation in complex systems. In : Kauffman SA, editor. The origins of order: self-organization and selection in evolution. New York: Oxford University Press;1993. p. 173–235.
19. Russell AP, Thomason JJ. Mechanical analysis of the mammalian head skeleton. In : Hanken J, Hall BK, editors. The skull. Vol. 3. Chicago: University of Chicago Press;1993. p. 345–383.
21. White SC, Rudolph DJ. Alterations of the trabecular pattern of the jaws in patients with osteoporosis. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 1999; 88:628–635.

22. Landis JR, Koch GG. The measurement of observer agreement for categorical data. Biometrics. 1977; 33:159–174.

23. Mommaerts MY. Transpalatal distraction as a method of maxillary expansion. Br J Oral Maxillofac Surg. 1999; 37:268–272.

24. Alpern MC, Yurosko JJ. Rapid palatal expansion in adults with and without surgery. Angle Orthod. 1987; 57:245–263.
25. Capelozza Filho L, Cardoso Neto J, da Silva Filho OG, Ursi WJ. Non-surgically assisted rapid maxillary expansion in adults. Int J Adult Orthodon Orthognath Surg. 1996; 11:57–66.
27. Lee RL, Dacre JE, James MF. Image processing assessment of femoral osteopenia. J Digit Imaging. 1997; 10:3 Suppl 1. 218–221.

28. Majumdar S, Lin J, Link T, et al. Fractal analysis of radiographs: assessment of trabecular bone structure and prediction of elastic modulus and strength. Med Phys. 1999; 26:1330–1340.





 PDF
PDF ePub
ePub Citation
Citation Print
Print






 XML Download
XML Download