Survival Analysis of Gastric Cancer Patients with Incomplete Data

Abbas Moghimbeigi; Lily Tapak; Ghodaratolla Roshanaei; Hossein Mahjub

doi:10.5230/jgc.2014.14.4.259

Abstract

Purpose

Survival analysis of gastric cancer patients requires knowledge about factors that affect survival time. This paper attempted to analyze the survival of patients with incomplete registered data by using imputation methods.

Materials and Methods

Three missing data imputation methods, including regression, expectation maximization algorithm, and multiple imputation (MI) using Monte Carlo Markov Chain methods, were applied to the data of cancer patients referred to the cancer institute at Imam Khomeini Hospital in Tehran in 2003 to 2008. The data included demographic variables, survival times, and censored variable of 471 patients with gastric cancer. After using imputation methods to account for missing covariate data, the data were analyzed using a Cox regression model and the results were compared.

Results

The mean patient survival time after diagnosis was 49.1±4.4 months. In the complete case analysis, which used information from 100 of the 471 patients, very wide and uninformative confidence intervals were obtained for the chemotherapy and surgery hazard ratios (HRs). However, after imputation, the maximum confidence interval widths for the chemotherapy and surgery HRs were 8.470 and 0.806, respectively. The minimum width corresponded with MI. Furthermore, the minimum Bayesian and Akaike information criteria values correlated with MI (-821.236 and -827.866, respectively).

Conclusions

Missing value imputation increased the estimate precision and accuracy. In addition, MI yielded better results when compared with the expectation maximization algorithm and regression simple imputation methods.

Introduction

According to statistics published by the World Health Organization (WHO) in 2010, most deaths occur from noncontiguous diseases. According to the statistics, more than 36 million deaths in 2008 were related to noncontiguous diseases, of which 48%, 21%, and 12% were related to heart disease, cancer and respiratory disease, respectively.1 In Iran, cancer is the third-leading cause of death after heart disease and accident. According to the most recent statistics from the Iran Cancer Research Center, in Iran gastric cancer is the most common type of cancer among men and the third-most common type among women.2,3

The prognosis of gastric cancer is usually poor,4,5 and therefore this disease has a high mortality rate. Given the low survival rate of such patients, it is very important to determine the factors that influence survival in gastric cancer patients. In Iran, various studies of gastric cancer patients6,7,8,9,10 and factors influencing their survival have been conducted using Cox regression modeling. Survival data analysis and modeling in the context of missing covariates present three major problems: 1) reduced efficacy because of the irregular information structure and complexity; 2) the lack of ability to use available software intended to analyze complete data; and 3) biased parameter estimation because of differences between observed and non-observed data.11 Most researchers exclude subjects with at least 1 missing data point, resulting in a large amount of data and analytical inefficacy. Ignoring these missing data leads to biased estimations results, especially when there is a difference between the survival durations of patients with at least 1 missing data point and that of patients with complete data.11

Understanding the mechanism of missing data is a substantial issue when performing an analysis. There are three mechanisms of missing data, as follows: when the variable with missing data is independent of the other variables, the missing data are considered missing completely at random (MCAR); when the variable with missing data is dependent on the observed data, the missing data are called missing at random (MAR); and finally, when the variable is dependent on missing values, the missing data are missing not at random. In the first two cases, the mechanism of missing data is ignored11 because the negative effects of missing data on the estimates are unavoidable and the missing data can be imputed. There are two types of imputation: simple imputation and multiple imputation (MI). In simple imputation, there is only imputed 1 value for a missing value, whereas in MI more than 1 independent values are obtained from imputation model to replace each missing value, and therefore m completed sets of data are obtained.11

The aim of this study was to conduct a comprehensive comparison of the results of registered factors that affect gastric cancers. To achieve this, we analyzed primary data with missing values using two simple imputation methods, regression and expectation maximization (EM) algorithm, and one MI method based on the Monte Carlo Markov Chain (MCMC).

Materials and Methods

1. Data

In this paper, data related to the survival of 471 gastric cancer patients who were referred to the cancer institute at Imam Khomeini Hospital, Tehran in 2003 to 2008 were investigated. The study variables included demographic data such as the age at diagnosis and sex; degree of tumor differentiation based on WHO criteria (weak, moderate, or good); tumor site (cardia, body, or antrum); tumor size (cm), pathological stage based on the American Joint Committee on cancer, 6th edition (II, III, or IV); treatment type, including chemotherapy (adjuvant, neoadjuvant, or palliative), radiotherapy, or surgery (resection or palliative bypass; yes/no); and weight loss (yes/no). Patient survival was registered from the time of diagnosis to death or the end of the study. Subjects who could not be contacted directly or who did not die before the end of the study were considered censored observations.10 All tests were conducted at a significance level of 0.05.

2. Cox proportional hazards model

To identify the factors influencing patient survival, we used a general form of the Cox proportional hazards model12:

h (t, X_{1}, ⃛, X_{p}) = h_{°} (t) exp (\sum_{i = 1}^{p} β_{i} X_{i})

The proportional hazards hypothesis was evaluated with a goodness of fit test.

This model was evaluated in complete cases and after completing a data set consisting of missing data via the three imputation methods. Although there are many imputation methods, the performance of these methods depends on the percentage of missing values, missing data pattern, type, and number of variables, and sample size. In this work, two simple imputation methods, regression and EM algorithm, and a MI method based on MCMC were used to impute absent values in a real data set, followed by a comparison of the results.

3. Complete case analysis

This method deletes all cases with at least 1 missing variable; accordingly, the analyses are conducted using cases in which all variables have been observed and there are no missing values. The MCAR hypothesis must be stated when using this method to obtain unbiased estimates. The complete case analysis is suitable for datasets with few missing values and a large sample size.

4. Regression imputation

In this method, missing values based on predictions from the regression model are imputed.11 The variable with missing values is considered a response variable and other variables are predicting variables; therefore, missing values are predicted as new observations through a fitted model. In this context, two types of logistic regression (for nominal and ordinal categorical variables) were used to handle categorical variables and multiple linear regressions were used for continuous variable imputations.

5. Expectation maximization algorithm

This iterative method is used to find the maximum likelihood of parameters in problems with missing data along with the simple imputation of missing data.13 This algorithm can be summarized in 4 stages: replacing the missing values with estimated values, estimation of parameters, re-estimation of the missing values assuming that the new parameter is correct, and a new estimation of parameters. The algorithm is repeated in a loop that continues to converge. If the matrix of data Y=(Y_obs, Y_mis) has a joint density function P(Y|θ) and log likelihood function l(Y|θ), the EM algorithm can be rewritten as follows:

θ^{(t + 1)} = \arg \max_{θ} E (l (θ | Y) Y_{o b s}, θ^{(t)})

6. Multiple imputations using the Monte Carlo Markov Chain method

MI has three steps. First, each missing value is imputed with a set of acceptable values that reflect uncertainty about the real value to be imputed. These multiple imputed data are subsequently analyzed using standard methods available for analyzing complete data, and multiple analyses are combined to yield the final results.

MI can be conducted using various methods, one of which is Gibbs sampling based on the MCMC methods. In this model, categorical variables are located among the cells of a table at the level intersections of these variables with multinomial marginal distributions. On each categorical variable level, continuous variables are considered to have multivariate normal distributions with means that differ among cells, and the covariance matrix is considered similar among all cells. In this model, the missing data mechanism is considered to be random and all hypotheses of this model are based on ignorable missingness.

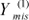Assuming the ignorable missingness mechanism, we can obtain m sets of imputed values in the form jgc-14-259-i003

, ...,

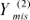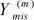of by using the Bayesian method and considering a prior distribution of θ. These imputed values are independent observations of the posterior density P(Y_mis|Y_obs)=∫P(Y_mis|Y_obs ,θ)P(θ|Y_obs)dθ. 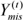To obtain the missing values, data augmentation was used in two steps; this represents a special case of Gibbs sampling in which updated values are obtained from conditional distributions in the case of jgc-14-259-i006

and θ^(t) in the t^th iteration, as follows:

Y_{m i s}^{(t + 1)} = P (\frac{Y_{m i s}}{Y_{o b s, θ^{(t)}}})

θ^{(t + 1)} = P (\frac{θ}{Y_{o b s}, Y_{m i s}^{(t + 1)}})

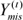Under reasonable conditions such as t→∞, the values of (θ^(t), jgc-14-259-i007

become stationary and the missing values are obtained from this distribution after convergence. The EM algorithm is used to generate the initial data augmentation values. In the MI method, 5 data sets were generated, and each of the 5 imputed sets were analyzed using the Cox regression model; we then combined the rules to obtain the final results. In this method, each data set is analyzed separately, and the results are combined according to specific rules to yield a general result comprising uncertainty about the missing data.14

7. Statistical software

Cox proportional hazard model fitting and regression imputation were performed using SPSS ver. 16.0 (SPSS Inc., Chicago, IL, USA). A MIX package of R software (version 2.15.1; Institute for Statistics and Mathematics, Vienna University of Economics and Business, Vienna, Austria; available at http://www.r-project.org/index.html) was used for MI and EM algorithm imputation (imp.mix and da.mix functions).

Results

Overall, 153 patients (32.5%) died; the remaining patients were censored at the end of the study or dropped out. The mean patient survival time after diagnosis was 49.1±4.4 months, with a maximum survival time of 125 months. Table 1 lists the demographic and clinical characteristics of the patients as percentages along with data missingness information. As shown in Table 1, the following variables have missing values: tumor differentiation degree (12.1%), tumor site (14.2%), tumor size (54.8%), pathological stage (50.5%), chemotherapy (3.2%), radiotherapy (4.9%), surgery (4.5%), and weight loss (39.9%). The overall missing data rate was 79%, requiring the removal of 371 of the 471 patients.

Regarding the missing data problem, the missing data proportion is not the only criterion for imputation. The missing data mechanisms and patterns have greater impacts on research results than does the missing data proportion.15 In order to obtain reliable results from the imputation, acceptance of the MAR or MCAR hypothesis is a key assumption. In the present study, Little's MCAR test16 was performed using SPSS ver. 16.0 and the MCAR assumption was not rejected (P=0.658). In addition, we considered the missing and non-missing data as two separate groups for all variables. We then compared the gender and age of the groups using the chi-square test and t-test. All P-values exceeded 0.05 and confirmed the assumption of MCAR for these data.

Table 2 lists coefficients of the variables in a Cox regression model before and after imputation along with the percentages of missing variables, standard errors, P-values, and hazard ratios (HRs) with 95% confidence intervals (CIs). The complete case analysis setting only used information from 100 of the 471 patients. The proportionality assumption for all variables was evaluated by including the time-dependent covariates. In this regard, the time-dependent covariates were generated by creating interactions between the predictors and a function of survival time (logarithm of time) and were included in the model. Based on the goodness of fit test, the proportional hazard hypothesis was supported. The generated time-dependent covariates were not significant (P>0.05).

As seen in Table 2, the age at diagnosis was the only significant variable in the complete case data analysis (P<0.001). In addition, very large and uninformative CIs were obtained for the chemotherapy and surgery variable HRs. This problem was not observed after imputation. After a regression imputation of the missing values, the variables of sex, age at diagnosis, tumor differentiation degree (weak), and pathologic stage (IV) were found to be significant (P<0.001). Furthermore, after MI the variables of sex, age at diagnosis, tumor differentiation degree (weak), and pathologic stage (IV) were found to be significant (P<0.001). In addition to the significant variables identified via MI, the variable of pathological stage (III) was significant in the EM algorithm imputation.

Furthermore, Table 2 shows that after imputation, the widths of the HR CIs were reduced; also, the CIs corresponding to MI were narrower than the others.

The Bayesian information crirerion (BIC) and Akaike information criteria (AIC) values have been calculated for the gastric cancer data subjected to the three imputation methods and complete case analysis. The minimum BIC and AIC values correlated with the MI (-821.236 and -827.866, respectively).

Discussion

This study evaluated the performances of two simple imputation methods and the MI method with respect to missing data and compared the results of these techniques with the result of a complete case analysis of gastric cancer data.

Diagnosis of the prognostic factors of gastric cancer is very important when determining the type of treatment. The effects of the imputation methods were compared after a Cox regression model evaluation. The results of the present study indicate that the CIs corresponding to the imputed data sets were narrower than that of the complete analysis, indicating improved estimate precision. Generally, a wider interval implies a less efficient approach. MI is the best approach in terms of efficiency because it yielded the narrowest CI. Furthermore, the complete case analysis yielded the worst results based on this criterion. Additionally, the MI performance was superior according to the BIC and AIC criteria for comparing models. The key point in the present study analysis is that imputation techniques improved the identification of factors that influence survival. We found that the variables of sex, age at diagnosis, tumor differentiation degree (weak), and pathologic stage (IV) all had significant effects on survival in gastric cancer patients.

In the MI setting, missing data were imputed five times to provide highly accurate estimates and avoid random effects on imputation. Two other imputation techniques (EM algorithm and regression) are also suitable when working with missing data. However, these techniques only replace each missing value with a single value. Accordingly, imputation uncertainty and estimate precision are not taken into account and may be diminished because of the high proportion of missing data.17 In this regard, single imputation cannot represent any additional uncertainty that might arise when the reason for data missingness is unknown.

In addition, even if the proportion of missing data for each variable is low, this may cause serious problems in multivariate modeling when patients with missing data are scattered throughout the dataset.17 This is because the number of complete cases available for analysis might be substantially reduced, thus increasing the risk of bias consequent to case exclusion. Power reduction is another consequence of complete case analysis, and case deletion may result in biased regression coefficients if the remaining cases are not representative of the entire sample.18

Several studies have confirmed the satisfactory performance of the MI technique in a simulation based on various criteria for handling missing covariates. Peng and Zhu,19 in a study to evaluate the performance of MI, concluded that MI had a lower bias and better efficiency and coverage with respect to estimating true parameter values than did the EM algorithm and complete case analysis.

In their study, Baneshi and Talei17 showed that the exclusion of cases with missing data led to bias and imprecise estimates and suggested that missing data imputation should be a primary step before conducting any modeling. Molenberghs et al.,20 in a study to compare different imputation techniques, concluded with a strong recommendation for MI. In addition, Marshall et al.21,22 concluded that MI might be the preferred approach for handling data missingness. Accordingly, the results of the present study confirm those previous findings.

Generally, invalid results are the usual consequence of excluding cases with missing data and analyzing only those subjects with complete data (complete case analysis).

Instead, before conducting any analysis, a close examination should be conducted in an attempt to understand the reasons for data missingness. Once the MCAR or MAR mechanism is assumed, missing data imputation should be performed before any modeling practice.

However, these results are only based on a single realistic population and the MCAR mechanism. Therefore, a limitation of this study is that the obtained results are not fully generalizable to other populations with differing distributions, correlations, and missing data mechanisms; hence, further studies are required.

This study addressed the performance of three imputation techniques with respect to a realistic data set from gastric cancer patients. Based on two evaluation criteria, the performance of MI was superior to that of simple imputation techniques of EM algorithm and regression. Furthermore, these three imputation methods yielded better performances than the complete case analysis. However, further studies are required because these results were based only on a single data set.