Journal List > Healthc Inform Res > v.23(1) > 1075869

TOOLS
Cho, Kim, Chae, and Song: Application of Queueing Theory to the Analysis of Changes in Outpatients' Waiting Times in Hospitals Introducing EMR
Original Article

Healthcare Informatics Research 2017; 23(1): 35-42.

Published online: 31 January 2017

DOI: https://doi.org/10.4258/hir.2017.23.1.35

Application of Queueing Theory to the Analysis of Changes in Outpatients' Waiting Times in Hospitals Introducing EMR

Kyoung Won Cho, PhD1, Seong Min Kim, BS1, Young Moon Chae, PhD2, Yong Uk Song, PhD3

1Department of Healthcare Administration, Kosin University, Busan, Korea.

2Graduate School of Public Health, Yonsei University, Seoul, Korea.

3Division of Business Administration, Yonsei University Wonju Campus, Wonju, Korea.

Corresponding Author: Yong Uk Song, PhD. Division of Business Administration, Yonsei University Wonju Campus, 1, Yeonsedae-gil, Heungeop-myeon, Wonju 26493, Korea. Tel: +82-33-760-2340, yusong@yonsei.ac.kr

Received 2 November 2016       Revised 24 January 2017       Accepted 25 January 2017

© 2017 The Korean Society of Medical Informatics

(open-access):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Objectives

This research used queueing theory to analyze changes in outpatients' waiting times before and after the introduction of Electronic Medical Record (EMR) systems.

Methods

We focused on the exact drawing of two fundamental parameters for queueing analysis, arrival rate (λ) and service rate (µ), from digital data to apply queueing theory to the analysis of outpatients' waiting times. We used outpatients' reception times and consultation finish times to calculate the arrival and service rates, respectively.

Results

Using queueing theory, we could calculate waiting time excluding distorted values from the digital data and distortion factors, such as arrival before the hospital open time, which occurs frequently in the initial stage of a queueing system. We analyzed changes in outpatients' waiting times before and after the introduction of EMR using the methodology proposed in this paper, and found that the outpatients' waiting time decreases after the introduction of EMR. More specifically, the outpatients' waiting times in the target public hospitals have decreased by rates in the range between 44% and 78%.

Conclusions

It is possible to analyze waiting times while minimizing input errors and limitations influencing consultation procedures if we use digital data and apply the queueing theory. Our results verify that the introduction of EMR contributes to the improvement of patient services by decreasing outpatients' waiting time, or by increasing efficiency. It is also expected that our methodology or its expansion could contribute to the improvement of hospital service by assisting the identification and resolution of bottlenecks in the outpatient consultation process.

Keywords: Electronic Medical Record, Healthcare, Queue, Waiting Time

I. Introduction

Hospitals are doing their best to provide a variety of medical services to increase patients' satisfaction. In particular, they have introduced Electronic Medical Record (EMR) systems to enhance their business efficiency and the quality of medical services [1]. However, public hospitals, which are less competitive than private hospitals, are one step behind in introducing EMR. Therefore, the Korean government has begun to implement EMR systems in public hospitals, such as Incheon Medical Center [2], Busan Medical, Gunsan Medical Center, and medical centers in the Gyeongbuk region [3].
It is known that the introduction of EMR has the effect of reducing outpatients' waiting times [4]. Many changes in business process regarding chart management have been reported because there is no need to deliver charts manually from storage to the medical office with the introduction of EMR. Hence, there is a need to investigate how much processing time is reduced in departments influenced by the introduction of EMR.
Previous studies regarding waiting time in medical services have focused on doctors and patient consultations in general hospitals [5]. Such studies found that the factors influencing consultation and waiting times are medical providers' characteristics, characteristics related to consultation, and patients' characteristics [6] as well as consultation department, whether a patient had an appointment or not, whether the patient was a new outpatient or not, patients' perceived consultation waiting times, patients' endurable waiting times [7], and so forth.
Studies applying queueing theory to medical service can be classified into those on waiting time and utilization analysis [8], those on system design satisfying some conditions regarding queueing [910], and those on the relation between appointment systems and queueing. From the perspective of system size, they have been conducted at the levels of the department, the healthcare center, and the regional health system [11]. Studies conducted at the department level include those conducted at Departments of Internal Medicine [6], Orthopedics [8], Emergency Room [1213], Radiology [10], and MRI [14]. Studies conducted at the healthcare center level include those conducted on a whole outpatient department [5715]. Studies on waiting time and utilization analysis can be further classified into those on reneging [111617], variable arrival rate [18], priority queueing discipline [1920], and blocking [21]. Studies on system design can be further classified into those on blocking [22] and cost minimization [2324]. Studies on the relation between appointment systems and queue include those considering bottlenecks and those on appointment and patient financial services [25].
In addition, previous studies on waiting time related to the introduction of hospital information systems include a study on the reduction of waiting time, which was conducted by surveying and investigating a specific hospital [4]. However, we could not find any previous studies that have made use of queueing theory to investigate changes in outpatient waiting times before and after the introduction of EMR. Therefore, in this research, we investigated changes in the outpatient waiting times before and after the introduction of EMR by applying queueing theory.
The remainder of this paper is organized as follows. First, Section II addresses queueing theory and explains our proprietary method to calculate waiting times. Section III analyzes changes in outpatient waiting times before and after the introduction of EMR in some Korean public hospitals, which were calculated by the proposed method. Finally, Section IV discusses some implications of our findings and draws some conclusions.

II. Methods

To investigate changes in outpatient waiting times before and after the introduction of EMR by applying queueing theory, we review queueing theory briefly and then explain our approach to examine outpatients' waiting times, which includes data collection and the calculation of arrival and service rates.

1. Queueing Theory

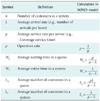
Patients who want to receive medical services always arrives randomly, and they require immediate services available at that time. If the service facility is operating at peak capacity when they arrive, they should wait in line with patience. At this point, according to the difference between the patients' arrival rate and the time required for services, a queue, in which the patients wait to be served, is formed. Due to the characteristics of medical services, it is very difficult to predict exactly when a patient will arrive and how much time will be taken for the service. Therefore, the ultimate objective of queueing theory is to achieve an economic equilibrium between the service cost and the patients' wasted time while waiting in the queue to be served. Measurement scales for a queueing system include the average number of customers in its queue (Lq), the average number of customers in its entire system including the entity being served (Ls), the average waiting time in its queue (Wq), and the average waiting time in its entire system (Ws). The symbols and concepts for a queueing model are presented in Table 1.

2. Our Approach

We analyze outpatients' waiting time using digital data, such as booking time, blood pressure measurement time, prescription input time, and payment reception time of patients who have visited public hospitals. There is, however, a variety of outpatient consultation paths as seen in Figure 1. In particular, since there are cases in which a nurse processes several patients' bookings collectively after consultation without individual booking, as in path 4 in Figure 1, and doctors input prescriptions after payment without booking, as in path 5 or 6, we can say that the booking times in the digital data are distorted and cannot reflect the outpatients' true waiting times. In addition, if we remove those distorted data with a naive intention to use correct data only, it would decrease the number of consultations and would result in the underestimation of measurements, including waiting time, number of customers in the queue, and so forth.
We focus on the exact drawing of two fundamental parameters from the digital data for queueing analysis, namely, the arrival rate (λ) and the service rate (µ), to overcome these problems. If we know the exact values of the arrival rate and the service rate, we can calculate the average waiting time in a queue (Wq) as in Table 1. Thus, it is possible to measure the decrease in outpatients' waiting times before and after the introduction of EMR.
Almost all queueing models assume the probability distribution of the interarrival time and the service time as an exponential distribution, and the number of arriving patients per unit of time follows Poisson distribution. Therefore, we assume that the probability distributions of the interarrival and service times are exponential. Furthermore, because the purpose of this research was to analyze the change in outpatients' consultation time in terms of a hospital and as a result, the number of the server is one in this case, we use the queueing model of M/M/1 for the analysis.

1) Data collection

We collected digital and observation data from three public hospitals that had introduced EMR systems as part of a local hospital information support initiative by the Korea Ministry of Health and Welfare in 2014. These public hospitals introduced new EMR systems on March 23, March 24, and April 13, 2015, respectively. Observers collected data by recording the time when a patient was called and entered the doctor's room and the time when the consultation was finished and the patient came out of the room. The digital data were collected for the weeks during which the observation was performed. The digital data were extracted from databases in public hospitals, which existed even before the introduction of EMR. Patients' names and gender information were masked for their privacy, and we used logs of reception times and prescription input times in seconds. Basic information on study hospitals for the three public hospitals, namely, Hospitals A, B and C, are shown in Table 2.

2) Calculation of arrival rate

There are two ways to calculate the arrival rate. One is to calculate the average interarrival times and then take its inverse number; the other is to take the average number of arrivals, and these two numbers must be equal. As seen in Table 3, the difference between the first patient's arrival time 9:01:10 (arrival 0) and the last patient's arrival time 9:47:55 (arrival 10) in data 1 is 46 minutes and 45 seconds or 2,805 seconds. By dividing the 2,805 seconds by the average interarrival time of 280.5 seconds, we obtain 10, which is the number of arrived patients except the first patient or arrival 0.
We calculate the arrival rate by using the reception time as the patient's arrival time. However, since nurses sometimes process reception collectively in public hospitals, we can say that the reception time data are distorted, and those reception times are not exactly equal to the true arrival times. However, the average interarrival time is not changed because the interarrival times for other reception times are increased as much when the interarrival times for the reception times input collectively by nurses are decreased to zero. As an example of arrival 6 in Table 3, even though the arrival time 9:43:48 in data 1 is changed to 9:23:48 in data 2, the average interarrival time is unchanged and maintains the value of 280.5 seconds. Therefore, there is no change in the calculated value of the arrival rate. As a result, we can obtain the exact arrival rate from the digital reception time data regardless of the distortion of the data by collective input.
On the other hand, consultation time in hospitals includes lunch time from 12:30 to 13:30, and receptions rarely occur during lunch time. If we do not consider lunch time and use the daily reception time data from 9:00 to 17:00 to calculate the arrival rate, the average interarrival time, which includes a relatively long interarrival time during lunch time, is overestimated. As a result, the arrival rate is underestimated. Moreover, the total consultation time is 7 hours per day excluding lunch time, while the reception time data include the data during 8 hours per day, which results in dissonance between the consultation time period (7 hours) and reception time period (8 hours) per day. For this reason, we calculate the arrival rate considering lunch time. We divide a day into morning and afternoon, classify the reception data into the data before 12:30 and the data after 12:30, and we calculate interarrival times for each set of data separately. Using the entire data for the dates when we collected the data, we calculate the average interarrival time and, finally, we calculate the arrival rate. This arrival rate is exactly equal to the average number of arrivals for the mornings and afternoons of the dates when we collected the data.

3) Calculation of service rate

Digital data in hospitals usually do not include a patient's consultation start time and finish time. The consultation, however, finishes with prescription input, so we use the prescription input time as the consultation finish time. Nevertheless, there is no consultation start time in the digital data. However, when a doctor treats patients in succession, a patient's consultation start time is the previous patient's consultation finish time, so we can use the previous patient's consultation finish time, that is, prescription input time, as the patient's consultation start time. In other words, the time period between a patient's prescription input time and his/her previous patient's prescription input time is the consultation time or service time for the patient, and the inverse number of the average consultation time is the service rate.
The important point here is that we must exclude the data for cases in which the doctor does not treat patients in succession and a patient's consultation start time is not equal to the previous patient's prescription input time. Considering these cases, we calculate the service rate by excluding the outlier data among those service times. In this study, however, it was impossible to identify the outlier data from the digital data in hospitals, so we used the observation data for consultation time acquired by an observer who actually visited public hospitals and carried out the observation work. However, since we could not find a statistical significance in using the observation data due to its limitation in the number of the data, we use those observation data just for support. That is, instead of obtaining the service rate by averaging the observed consultation times, we used the maximum of the observed consultation times to identify outliers, and we averaged the consultation time from the digital data in hospitals after excluding the consultation times of which the value was greater than the maximum observed consultation time. After that, we used the inverse number of the average as the service rate.
We carried out a t-test to verify whether there was any difference between the service rates obtained from the digital and observed data (Table 4). Since we were able to conduct observation during just one day, we used digital data for the same day of observation. The differences between the average service rates were 67.47 and 14.9 in the first and second investigations in Hospital A, 12.68 and 25.37 in Hospital B, and 65.66 and 58.06 in Hospital C. We found that there was no statistically significant difference between the service rates obtained from digital and observed data except in the first investigation in Hospital A, where the service rates from the digital and observed data were statistically significantly different with the p-value of 0.001. Although we cannot argue the consistency of the service rates statistically because only six comparison data sets were considered, we may claim that the service rates from the digital and observed data were similar to each other and the service rates obtained from digital data, which were based on huge data sets, were more accurate than the service rates obtained from observed data, which were based on a limited number of data sets.

III. Results

We analyzed the changes in outpatients' consultation waiting times before and after the introduction of EMR by applying the proposed method to calculate the waiting times. We obtained and compared outpatients' waiting times before and after the introduction of EMR in three public hospitals, namely, Hospitals A, B and C.
We carried out queueing analysis for outpatients' waiting times before and after the introduction of EMR and investigated the changes in waiting time (Table 5). In the case of Hospital A, the patients' average waiting times in a queue were 221.75 and 49.33 seconds before and after the introduction of the system, for which the decrease rate was 77.75%. In the case of Hospital B, the patients' average waiting times in a queue were 94.23 and 50.87 seconds before and after the introduction of the system, for which the decrease rate was 46.02%. In the case of Hospital C, the patients' average waiting times in a queue were 177.64 and 98.49 seconds before and after the introduction of the system, for which decrease rate was 44.56%. We obtained the waiting times from observation data as well to verify the decrease in waiting time obtained from digital data; thus, we could confirm that the outpatients' waiting times decreased after the introduction of EMR. The average waiting time in all of the three hospitals were 150.62 and 60.34 seconds before and after the introduction of the system, for which the decrease rate was 59.94%.

IV. Discussion

We analyzed the changes in outpatients' waiting times before and after the introduction of EMR using the proposed method. According to the analysis result, the outpatients' waiting times in three public hospitals decreased after the introduction of EMR, which coincides with the research by [4]. In addition, we calculated waiting times using observation data to confirm the decrease in waiting time obtained using digital data. Moreover, the decrease in waiting times based on both the observation and digital data were in the range between 44% and 78%, which is relatively high. However, the investigated hospitals had relatively small numbers of outpatients, which resulted in relatively few substantial waiting times, and most of the waiting time was taken up by manual chart management, the elimination of which resulted in sharply decreased waiting times. Thus, our results verify that the introduction of EMR contributes to the improvement of patient services by decreasing outpatients' waiting time or by increasing efficiency [6].
This research had some limitations. First, even though we used many digital data from three hospitals for a t-test to verify the service rates, we may need more data sets than the six from the three hospitals to argue the statistical significance and generalize our approach. Furthermore, the result of reduction in waiting times might differ according to the size of the hospital. Large hospitals usually provide their services based on appointment, which results in a shorter time for chart delivery, which in turn results in a smaller reduction in waiting times. Hence, extended studies considering hospital size with more data sets are recommended.
In sum, the analysis of changes in waiting time using observation data gathered by an observer in the field is time consuming and has some limited generalizability due to special situations during consultations. It is, however, possible to analyze waiting times while minimizing the input errors and limitations influencing consultation procedures if we use digital data and apply queueing theory. It is expected that the proposed method or its expansion could contribute to the improvement of hospital services by helping to identify and resolve bottlenecks in the outpatient consultation process.

Figures and Tables

Figure 1

Patient consultation paths.

hir-23-35-g001
Table 1

Symbols for queueing model and calculation in M/M/1 model

hir-23-35-i001
Table 2

Basic information on study hospitals

hir-23-35-i002
Table 3

Calculation of arrival rate

hir-23-35-i003
Table 4

The t-test for service rate

hir-23-35-i004
Table 5

Changes in outpatients' waiting time

hir-23-35-i005

aCutting criteria. bDecrease rate = (A – B) / A × 100.

Acknowledgments

This research was supported by the “Performance evaluation program of information systems for the regional public hospitals” funded by the Ministry of Health and Welfare.

Notes

Conflict of Interest No potential conflict of interest relevant to this article was reported.

References

1. Jeong BH, Choi JT, Park SS. An implementation of medical treatment schedule guidance system for inpatients satisfaction improvement. J Korean Inst Inf Technol. 2012; 10(2):88–93.
2. Chae YM, Cho KW, Kim HS, Park CB. Evaluation of hospital information system based on the performance reference model. Korean J Health Serv Manag. 2011; 5(1):1–13.
crossref
3. Cho KW, Bae SK, Ryu JH, Kim KN, An CH, Chae YM. Performance evaluation of public hospital information systems by the information system success model. Healthc Inform Res. 2015; 21(1):43–48.
crossref
4. An CH. Study on the economic analysis of hospital information system for regional medical center [dissertation]. Seoul, Korea: Yonsei University;2013.
5. Park SH. Analysis of factors delaying on waiting time for medical examination of outpatient on a hospital. J Korean Soc Qual Assur Health Care. 2001; 8(1):56–72.
6. Hwang JI. Factors influencing consultation time and waiting time of ambulatory patients in a tertiary teaching hospital. Qual Improv Health Care. 2006; 12(1):6–16.
7. Ko YK. The relationships among waiting time, patient's satisfaction, and revisiting intention of outpatients in general hospital. J Korean Acad Nurs Adm. 2010; 16(3):219–228.
crossref
8. Yeo H, Bak W, Yoo M, Park S, Lee S. Evaluation of patients' queue environment on medical service using queueing theory. J Korean Soc Qual Manag. 2014; 42(1):71–79.
crossref
9. Green LV, Soares J, Giglio JF, Green RA. Using queueing theory to increase the effectiveness of emergency department provider staffing. Acad Emerg Med. 2006; 13(1):61–68.
crossref
10. Park CK, Kwag EJ. A case study about managing waiting time for raising customer's satisfaction in the medical service. Korean J Hosp Manag. 2009; 14(3):132–153.
11. HallR. BelsonD. MuraliP. DessoukyM. Modeling patient flows through the health care system. In : Hall R, editor. Patient flow. New York (NY): Springer;2013. p. 3–42.
12. Kim S, Seo H, Lee J, Kwon Y, Kim S, Park I, et al. An application of a queueing network for waiting time reduction at the emergency care center. Proceedings of the Korean Operations and Management Science Society Conference. 2009 Oct 30; Seoul, Korea. p. 298–316.
13. Mandelbaum A, Momcilovic P, Tseytlin Y. On fair routing from emergency departments to hospital wards: QED queues with heterogeneous servers. Manag Sci. 2012; 58(7):1273–1291.
crossref
14. Green LV, Savin S. Reducing delays for medical appointments: a queueing approach. Oper Res. 2008; 56(6):1526–1538.
crossref
15. Kim S, Son U, Choi J, Roh J, Yang Y. Analysis of factors delaying on waiting time of outpatient in a general hospital. Health Welf. 2008; 10:107–120.
crossref
16. Broyles JR, Cochran JK. Estimating business loss to a hospital emergency department from patient reneging by queuing-based regression. Proceedings of the 2007 Industrial Engineering Research Conference. 2007 May 19-23; Nashville, TN. p. 613–618.
17. Roche KT, Cochran JK. Improving patient safety by maximizing fast-track benefits in the emergency department: a queuing network approach. Proceedings of the 2007 Industrial Engineering Research Conference. 2007 May 19-23; Nashville, TN. p. 619–624.
18. Worthington DJ. Queueing models for hospital waiting lists. J Oper Res Soc. 1987; 38(5):413–422.
crossref
19. Green L. Queueing analysis in healthcare. In : Hall RW, editor. Patient flow: reducing delay in healthcare delivery. New York (NY): Springer;2006. p. 281–307.
20. Fiems D, Koole G, Nain P. Waiting times of scheduled patients in the presence of emergency requests [Internet]. place unknown: publisher unknown;2015. cited at 2016 Dec 3. Available from: http://www.math.vu.nl/~koole/publications/2005report1/art.pdf.
21. Koizumi N, Kuno E, Smith TE. Modeling patient flows using a queuing network with blocking. Health Care Manag Sci. 2005; 8(1):49–60.
crossref
22. de Bruin AM, van Rossum AC, Visser MC, Koole GM. Modeling the emergency cardiac in-patient flow: an application of queuing theory. Health Care Manag Sci. 2007; 10(2):125–137.
crossref
23. Gorunescu F, McClean SI, Millard PH. A queueing model for bed-occupancy management and planning hospitals. J Oper Res Soc. 2002; 53(1):19–24.
crossref
24. Gorunescu F, McClean SI, Millard PH. Using a queueing model to help plan bed allocation in a department of geriatric medicine. Health Care Manag Sci. 2002; 5(4):307–312.
25. Park CS, Koh SH. A case study on the improvement of general hospital outpatients waiting time using TOC methodology. Korean J Hosp Manag. 2011; 16(1):77–100.
TOOLS
Similar articles