1. Levey AS, Inker LA, Coresh J. Chronic kidney disease in older people. JAMA. 2015; 314(6):557–558.

2. Mills KT, Xu Y, Zhang W, Bundy JD, Chen CS, Kelly TN, et al. Abstract MP40: Global burden of chronic kidney disease in 2010: a pooling analysis of population-based data worldwide. Circulation. 2015; 131:Suppl 1. AMP40.
3. Saatchi M, Poorolajal J, Amirzargar MA, Mahjub H, Esmailnasab N. Long-term survival rate of kidney graft and associated prognostic factors: a retrospective cohort study, 1994-2011. Ann Transplant. 2013; 18:153–160.

4. White SL, Chadban SJ, Jan S, Chapman JR, Cass A. How can we achieve global equity in provision of renal replacement therapy? Bull World Health Organ. 2008; 86(3):229–237.

5. Hamidi O, Poorolajal J, Farhadian M, Tapak L. Identifying important risk factors for survival in kidney graft failure patients using random survival forests. Iran J Public Health. 2016; 45(1):27–33.
6. Hesketh CC, Knoll GA, Molnar AO, Tsampalieros A, Zimmerman DL. Vitamin D and kidney transplant outcomes: a protocol for a systematic review and meta-analysis. Syst Rev. 2014; 3:64.

7. Han J, Kamber M. Data mining: concepts and techniques. Amsterdam: Elsevier/Morgan Kaufmann;2000.
8. Tu JV. Advantages and disadvantages of using artificial neural networks versus logistic regression for predicting medical outcomes. J Clin Epidemiol. 1996; 49(11):1225–1231.

9. Delen D, Oztekin A, Tomak L. An analytic approach to better understanding and management of coronary surgeries. Decis Support Syst. 2012; 52(3):698–705.

10. Agresti A, Kateri M. Categorical data analysis. In : Lovric M, editor. International encyclopedia of statistical science. Heidelberg: Springer;2011. p. 206–208.
11. Linder R, Konig IR, Weimar C, Diener HC, Poppl SJ, Ziegler A. Two models for outcome prediction. Methods Inf Med. 2006; 45(5):536–540.

12. Caocci G, Baccoli R, Littera R, Orru S, Carcassi C, La Nasa G. Comparison between an artificial neural network and logistic regression in predicting long term kidney transplantation outcome. In : Suzuki K, editor. Artificial neural networks: architectures and applications. Rijeka, Croatia: InTech;2013.
13. Luck M, Sylvain T, Cardinal H, Lodi A, Bengio Y. Deep learning for patient-specific kidney graft survival analysis [Internet]. Ithaca (NY): arXiv.org;2017. cited at 2017 Oct 1. Available from:
https://arxiv.org/abs/1705.10245.
14. Ayat S, Farahani HA, Aghamohamadi M, Alian M, Aghamohamadi S, Kazemi Z. A comparison of artificial neural networks learning algorithms in predicting tendency for suicide. Neural Comput Appl. 2013; 23(5):1381–1386.

15. Lofaro D, Greco R, Papalia T, Bonofiglio R. Increasing levels of hemoglobin improve renal transplantation outcomes. Transplant Proc. 2011; 43(4):1036–1038.

16. Prasad GVR, Ananth S, Palepu S, Huang M, Nash MM, Zaltzman JS. Commercial kidney transplantation is an important risk factor in long-term kidney allograft survival. Kidney Int. 2016; 89(5):1119–1124.

17. Sert I, Colak H, Tugmen C, Dogan SM, Karaca C. The effect of cold ischemia time on delayed graft function and acute rejection in kidney transplantation. Saudi J Kidney Dis Transpl. 2014; 25(5):960–966.

18. Gonzalez-Molina M, Burgos D, Cabello M, Ruiz-Esteban P, Rodriguez MA, Gutierrez C, et al. Impact of immunosuppression treatment on the improvement in graft survival after deceased donor renal transplantation: a long-term cohort study. Nefrologia. 2014; 34(5):570–578.
19. Rostami Z, Shafighi N, Baghersad MM, Einollahi B. Risk factors for immediate anemia in renal transplant recipients: a single-center experience. Transplant Proc. 2011; 43(2):581–583.

20. Oetting WS, Guan W, Schladt DP, Wildebush WA, Becker J, Thyagarajan B, et al. Telomere length of recipients and living kidney donors and chronic graft dysfunction in kidney transplants. Transplantation. 2014; 97(3):325–329.

21. Gondos A, Dohler B, Brenner H, Opelz G. Kidney graft survival in Europe and the United States: strikingly different long-term outcomes. Transplantation. 2013; 95(2):267–274.
22. Ghadiani MH, Peyrovi S, Mousavinasab SN, Jalalzadeh M. Delayed graft function, allograft and patient srvival in kidney transplantation. Arab J Nephrol Transplant. 2012; 5(1):19–24.
23. Guliyev O, Sayin B, Uyar ME, Genctoy G, Sezer S, Bal Z, et al. High-grade proteinuria as a cardiovascular risk factor in renal transplant recipients. Transplant Proc. 2015; 47(4):1170–1173.

24. Ounissi M, Cherif M, Abdallah TB, Bacha M, Hedri H, Abderrahim E, et al. Risk factors and consequences of delayed graft function. Saudi J Kidney Dis Transpl. 2013; 24(2):243–246.

25. Lin CC, Chan HH, Huang CY, Yang NS. Predictive models for pre-operative diagnosis of rotator cuff tear: a comparison study of two methods between logistic regression and artificial neural network. Appl Mech Mater. 2014; (595):263–268.

26. Shi HY, Lee KT, Lee HH, Ho WH, Sun DP, Wang JJ, et al. Comparison of artificial neural network and logistic regression models for predicting in-hospital mortality after primary liver cancer surgery. PLoS One. 2012; 7(4):e35781.

27. Chen H, Zhang J, Xu Y, Chen B, Zhang K. Performance comparison of artificial neural network and logistic regression model for differentiating lung nodules on CT scans. Expert Syst Appl. 2012; 39(13):11503–11509.

28. Tapak L, Mahjub H, Hamidi O, Poorolajal J. Real-data comparison of data mining methods in prediction of diabetes in Iran. Healthc Inform Res. 2013; 19(3):177–185.

29. Lau L, Kankanige Y, Rubinstein B, Jones R, Christophi C, Muralidharan V, Bailey J. Machine-learning algorithms predict graft failure after liver transplantation. Transplantation. 2017; 101(4):e125–e132.

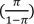 indicates the odds of classifying the response variable in category one than zero using several covariates and factors [10]. In the present study, we used the age and sex of donors and recipients, type of donor (living or deceased), etc. as covariates (χ) and having chronic nonreversible graft rejection as the binary response. Thus, π, is the probability of graft rejection.
indicates the odds of classifying the response variable in category one than zero using several covariates and factors [10]. In the present study, we used the age and sex of donors and recipients, type of donor (living or deceased), etc. as covariates (χ) and having chronic nonreversible graft rejection as the binary response. Thus, π, is the probability of graft rejection.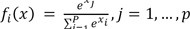 where xi's are predictor variables) in the output layer. The functional form of MLP is written as
where xi's are predictor variables) in the output layer. The functional form of MLP is written as
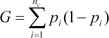 where nc shows the number of classes in the output variable, and pi stands for the ratio of this class.
where nc shows the number of classes in the output variable, and pi stands for the ratio of this class.



 PDF
PDF ePub
ePub Citation
Citation Print
Print


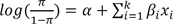
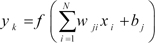





 XML Download
XML Download