Abstract
Objectives
Breast cancer has a high rate of recurrence, resulting in the need for aggressive treatment and close follow-up. However, previously established classification guidelines, based on expert panels or regression models, are controversial. Prediction models based on machine learning show excellent performance, but they are not widely used because they cannot explain their decisions and cannot be presented on paper in the way that knowledge is customarily represented in the clinical world. The principal objective of this study was to develop a nomogram based on a naïve Bayesian model for the prediction of breast cancer recurrence within 5 years after breast cancer surgery.
Methods
The nomogram can provide a visual explanation of the predicted probabilities on a sheet of paper. We used a data set from a Korean tertiary teaching hospital of 679 patients who had undergone breast cancer surgery between 1994 and 2002. Seven prognostic factors were selected as independent variables for the model.
The number of breast cancer patients is continually increasing. The prevalence of breast cancer in the female population of Korea was 16.7 per 100,000 in 1996 and 46.8 per 100,000 in 2006, a nearly threefold increase over a decade. Breast cancer is highly curable, but it is also notorious for having a high rate of recurrence (20%-30%). Of the patients with recurrence, 70.9% of patients experience a recurrence within 3 years of surgery, and 92% within 5 years in Korea. In one study, more than half of the patients who had a relapse of breast cancer had also a third attack of the cancer [1]. Thus, the period of treatment for breast cancer is long. To prevent breast cancer recurrence, it is important to predict such recurrence, to provide proper treatment immediately after surgery, and to identify breast cancer early.
Many studies have used a machine-learning algorithm to predict the recurrence of breast cancer [2345]. The most frequently used machine-learning algorithm is an artificial neural network (ANN) [23]. However, in a neural network, it is difficult to know the relationships between attribute values and classes. This is an issue of great importance in the clinical field. Physicians are not willing to use the so-called 'black box model' Because of its explainability, the naïve Bayesian classifier is a useful method for providing valuable insight into the structure of the decision-making process. The naïve Bayesian classifier is one of the simplest useful methods to provide predictive models for diagnosis, prognosis, and treatment planning from retrospective patient data. However, machine learning algorithms are not preferred by clinicians for medical predictions because prediction is difficult without a computer or calculator for probability calculation. A sheet of paper illustrating a simple flowchart or tables is the usual means of knowledge representation in the clinical world. Computer-based calculations are still far from most clinicians' minds. A nomogram is an intuitive, easy-to-interpret graph that can represent prediction models on a sheet of paper [6]. Thus, it can provide, in a simple form, the predicted probability of a specific outcome for an individual patient. The purpose of this study was to use the naïve Bayesian classifier to develop such a nomogram as a tool that is intuitive and easy to use in daily practice for the prediction of breast cancer recurrence within 5 years after breast cancer surgery.
We used clinical data obtained from the Breast Cancer Center of the Ajou University Medical Center in Korea. The data was previously reported and described [7]. This data pertained to breast cancer patients who had undergone breast cancer surgery during the years from 1994 to 2002, with at least a 60-month follow-up. The median follow-up of the patients was 86 months. A subset of 679 of the 733 patients was selected from the study participants by exclusion of males (n = 11), women with other multiple cancers (n = 14) or stage IV cancer (n = 7), and those with an unspecified follow-up time (n = 22) (Table 1).
An important challenge in the construction of a prognosisprediction model is the selection of prognostic factors. Ideally, all variables that improve the performance of the model should be used. However, practically, the selected variables must also be appropriate according to previously established clinical knowledge. Variables that are selected purely by statistical or machine learning methods without a clear clinical context are not easily accepted by the clinical community. This is a major reason that prediction models based purely on machine learning are not widely used, despite their superior prediction performance over traditional models. We used both previously established clinical knowledge and univariate analyses to select relevant independent variables for the prediction model (Figure 1). The variable selection process was described in detail in a previous report [7]. The clinical data contained 192 fields, including administrative, epidemiological, clinical, pathological, and post-surgery information. A total of 38 clinically relevant variables were preliminarily screened by a breast surgeon. Of these, 14 variables were selected during a second round of consensus meetings between a physician, a surgical pathologist, and a breast surgeon. For the final stage of prognostic factor selection, we used univariate analyses based on Pearson chi-square test for categorical variables and univariate logistic regression for continuous variables. The resulting seven statistically significant (p < 0.05) variables were histological grade, local invasion of tumor, number of tumors, tumor size, lymphovascular invasion, estrogen-receptor status, and the number of metastatic lymph nodes. A prediction model for breast cancer recurrence within 5 years after surgery was then constructed using a naïve Bayesian classifier. The model was transformed into a nomogram for representation on paper.
Visualization is one of the most intuitive methods of knowledge representation and is suitable for physicians in complex and busy clinical environments. A nomogram can reveal the structure of a naïve Bayesian classifier as well as the relative importance of the attributes. Thus, we decided to use both methods to fulfill the requisites. A naïve Bayesian classifier is a simple probabilistic classifier based on Bayes' theorem, with a strong assumption of the conditional independence of features relevant to the class. For the naïve Bayesian classifier, we used Laplace correction as a smoothing method to estimate posterior probabilities. Drawing a nomogram based on a naïve Bayesian has already been well established [8]. Under the independence assumption, the conditional probability P(c|X) for a sample X with a set of instance X = (a1, a2, ..., am) to be a member of class c is computed as follows:
Let c be the class for which a nomogram is constructed; the probability of the alternative class c is P(c|X).
The Odds for these two probabilities are defined as
Here, log it is defined as log Odds. This translates to
where OR is the odds ratios. Here, logit of class probability P(c|X) is determined by the sum of independent values of logOR of the attribute value (ai). This property is used for the construction of a nomogram that relates the feature values to the point score. Experts, such as statisticians, can interpret a scale using logOR points, but most clinicians may find it easier to use a scale with integer points from 0 to 100. Therefore, we used integer points in deference to clinical environments. To show the sum of individual point scores as a class probability, we start from equation (3) and F(c|X). Let F(c|X) equal the sum of logOR(ai). Equation (3) becomes and P(c|X) is computed as
The sum of the points, which forms the lower part of the nomogram, is then a function of P(c|X) = f(F(c|X)). It is linked by the known attributes to the class probability. This nomogram is a graphical calculating representation that is used by the total points to identify the probability of breast cancer recurrence within 5 years after breast cancer surgery. The naive Bayes classifier and nomogram visualization was implemented in the Orange data mining suite (University of Ljubljana, Ljubljana, Slovenia). The naïve Bayes classifier uses locally weighted scatterplot smoothing (LOESS) to estimate the conditional probabilities for continuous attributes. The size of the LOESS window and the LOESS sample points are 0.5 and 100, respectively. Figure 2 shows the proposed nomogram based on the constructed naïve Bayesian classifier.
For construction and performance assessment of the prediction model, we split the entire data sample into two mutually exclusive sets, one for training (70% of the data) and one for testing (the remaining 30%). The training set was used to generate the prediction model, and the testing set was employed to estimate the model's performance. Table 2 displays the characteristics of the training and test data sets.
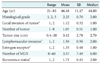
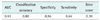
Figure 3A shows the receiver operating characteristics (ROC) diagram of the naive Bayesian classifier for the recurrence class. The area under the curve (AUC) is a statistically consistent and more discriminating measure than an accuracy measure [9] and a global summary statistic of diagnostic accuracy. AUC can distinguish among non-informative (AUC = 0.5), less accurate 0.5 < AUC ≤ 0.7), moderately accurate (0.7 < AUC ≤ 0.9), highly accurate (0.9 < AUC ≤ 1), and perfect tests (AUC = 1) [10]. In this study, the performance of the naïve Bayesian classifier was moderately accurate (AUC = 0.81) (Table 3). Using the testing data set, a calibration plot (Figure 3B) of class probabilities against those predicted by the naïve Bayesian classifier showed good calibration of the classifier.
Decisions about how to treat breast cancer patients after surgery are important to prevent the recurrence of breast cancer, yet predicting the disease outcome for an individual patient is a highly challenging task. Many studies have addressed the prediction of breast cancer recurrence, and the most frequently used methods have been traditional statistical analyses. The Cox proportional-hazard regression model is the standard survival analysis statistical technique for the analysis of time-to-event data due to the relative simplicity of the established statistical theory. However, Cox regression cannot be readily adapted to nonlinear problems [11]. For such problems, machine learning techniques are a well-known alternative to traditional regression methods [1213]. Machine learning techniques can perform extremely well for many medical problems, but significant limitations hinder their use in the real clinical world. One of these limitations is that clinicians and patients cannot easily use such a prediction model without a computer or calculator. Another is that they cannot provide valuable insight by exposing the relationships among attributes and classes. As a remedy to these problems, we applied a naïve Bayesian classifier to provide valuable insight and constructed a nomogram for visualization of the prediction model. The performance of the proposed model was similar to that of an SVM-based prediction model (AUC = 0.85) [7], or that of an ANN-based model (AUC = 0.85) [3]. However, this comparison had the limitation that the performance of the SVM and ANN was obtained from the published literature.
We selected seven relevant factors for the prediction model using a combination of clinical knowledge and statistical analysis. Variables selected purely by statistical analysis without clinical context are generally unacceptable to clinicians, even if the performance is superior. In this study, experienced clinicians selected 14 factors out of 192 potential factors through screening and multistep consensus meetings, and a final statistical method was used to confirm the final seven variables. All of the selected seven factors are well-known to clinicians and can be easily obtained from patients. In consideration of complex clinical environments, our proposed nomogram based on naïve Bayesian with simple variables should enhance acceptance of the model by clinicians. In clinical practice, clinicians have to decide whether or not to treat patients with various adjuvant therapies (chemotherapy, radiotherapy, hormone therapy, etc.) after surgery. However, if a breast cancer patient who has undergone surgery has a high predicted probability of recurrence in the proposed model, it will help the clinician to derive an aggressive adjuvant therapy for recurrence prevention of breast cancer. The proposed model can also help patients who have been provided with personalized adjuvant therapy to reduce their risk of breast cancer recurrence.
The proposed model showed moderate accuracy, thus it can be used in real clinical settings. However, it is necessary to evaluate the proposed model with external data for validation.
We have proposed a novel prognostic model predicting the risk of recurrence within 5 years after breast cancer surgery. This model can assist clinicians in the selection of appropriate adjuvant treatments for individual patients. This nomogram-based approach should be particularly useful for clinicians to compute the probability of breast cancer recurrence without depending on a computer or calculator.
Figures and Tables
 | Figure 1Process of selecting prognostic factors in the model using both previously established clinical knowledge and statistical analysis. |
 | Figure 2Proposed nomogram for the prediction of breast cancer recurrence within 5 years after breast cancer surgery. By using a measure, each score of the variables can be transferred into the total score, which is linked to the responding probability. |
 | Figure 3Receiver operating characteristics (ROC) curve and calibration plot for the naïve Bayesian classifier at 5 years after breast cancer surgery. (A) The area under the ROC curve (AUC) was 0.81 for naïve Bayesian classifier. (B) The x-axis represents the predicted probability of recurrence; the y-axis represents observed probability. TP: true positive, FP: false positive. |
References
1. Korean Breast Cancer Society. Breast cancer facts and figures 2006-2008. Seoul: Breast Cancer Society;2008. p. 1–16.
2. Bourdes VS, Bonnevay S, Lisboa PJ, Aung MH, Chabaud S, Bachelot T, et al. Breast cancer predictions by neural networks analysis: a comparison with logistic regression. In : Proceedings of 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBS); 2007 Aug 22-26; Lyon, France. p. 5424–5427.
3. Jerez JM, Franco L, Alba E, Llombart-Cussac A, Lluch A, Ribelles N, et al. Improvement of breast cancer relapse prediction in high risk intervals using artificial neural networks. Breast Cancer Res Treat. 2005; 94(3):265–272.

4. Jerez-Aragones JM, Gomez-Ruiz JA, Ramos-Jimenez G, Munoz-Perez J, Alba-Conejo E. A combined neural network and decision trees model for prognosis of breast cancer relapse. Artif Intell Med. 2003; 27(1):45–63.

5. Yi M, Buchholz TA, Meric-Bernstam F, Bedrosian I, Hwang RF, Ross MI, et al. Classification of ipsilateral breast tumor recurrences after breast conservation therapy can predict patient prognosis and facilitate treatment planning. Ann Surg. 2011; 253(3):572–579.

6. Mozina M, Demsar J, Kattan M, Zupan B. Nomograms for naive Bayesian classifiers and how can they help in medical data analysis. In : Proceedings of International Medical Informatics Association (MEDINFO2004); 2004 Sept 7-11; San Francisco, CA. p. 1762.
7. Kim W, Kim KS, Lee JE, Noh DY, Kim SW, Jung YS, et al. Development of novel breast cancer recurrence prediction model using support vector machine. J Breast Cancer. 2012; 15(2):230–238.

8. Mozina M, Demsar J, Kattan MW, Zupan B. Nomograms for visualization of naive Bayesian classifier. In : Boulicaut JF, Esposito F, Giannotti F, Pedreschi D, editors. Knowledge discovery in databases: PKDD 2004. Heidelberg: Springer;2004. p. 337–348.
9. Huang J, Ling CX. Using AUC and accuracy in evaluating learning algorithms. IEEE Trans Knowl Data Eng. 2005; 17(3):299–310.

10. Greiner M, Pfeiffer D, Smith RD. Principles and practical application of the receiver-operating characteristic analysis for diagnostic tests. Prev Vet Med. 2000; 45(1-2):23–41.

11. Aitkin M, Laird N, Francis B. A reanalysis of the Stanford heart transplant data. J Am Stat Assoc. 1983; 78(382):264–274.





 PDF
PDF ePub
ePub Citation
Citation Print
Print


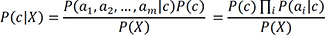
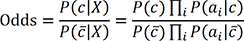
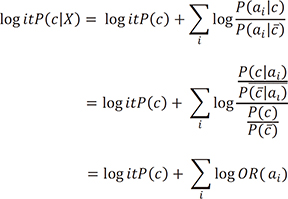
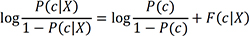

 XML Download
XML Download