1. Schoenhagen P, Stillman AE, Halliburton SS, White RD. CT of the heart: principles, advances, clinical uses. Cleve Clin J Med. 2005; 72(2):127–138.

2. Barandiaran I, Macia I, Berckmann E, Wald D, Dupillier MP, Paloc C, et al. An automatic segmentation and reconstruction of mandibular structures from CT-data. In : Proceedings of 10th International Conference on Intelligent Data Engineering and Automated Learning; 2009 Sep 23-26; Burgos, Spain. p. 649–655.
3. World Health Organization. The world health report 2003: shaping the future. Geneva, Switzerland: World Health Organization;2003.
5. Malladi R, Sethian JA, Vemuri BC. Shape modeling with front propagation: a level set approach. IEEE Trans Pattern Anal Mach Intell. 1995; 17(2):158–175.

6. van Assen HC, Danilouchkine MG, Dirksen MS, Reiber JH, Lelieveldt BP. A 3-D active shape model driven by fuzzy inference: application to cardiac CT and MR. IEEE Trans Inf Technol Biomed. 2008; 12(5):595–605.

7. Takagi T, Sugeno M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans Syst Man Cybern. 1985; 15(1):116–132.

8. Mitchell SC, Bosch JG, Lelieveldt BP, van der Geest RJ, Reiber JH, Sonka M. 3-D active appearance models: segmentation of cardiac MR and ultrasound images. IEEE Trans Med Imaging. 2002; 21(9):1167–1178.

9. Ecabert O, Peters J, Schramm H, Lorenz C, von Berg J, Walker MJ, et al. Automatic model-based segmentation of the heart in CT images. IEEE Trans Med Imaging. 2008; 27(9):1189–1201.

10. Funka-Lea G, Boykov Y, Florin C, Jolly MP, Moreau-Gobard R, Ramaraj R, et al. Automatic heart isolation for CT coronary visualization using graph-cuts. In : Proceedings of 3rd IEEE International Symposium on Biomedical Imaging: Nano to Macro; 2006 Apr 6-9; Arlington, VA. p. 614–617.
11. Grady L, Sun V, Williams J. Interactive graph-based segmentation methods in cardiovascular imaging. In : Paragios N, Chen Y, Faugeras O, editors. Handbook of mathematical models in computer vision. New York (NY): Springer;2006. p. 453–469.
12. Kanungo T, Mount DM, Netanyahu NS, Piatko CD, Silverman R, Wu AY. An efficient k-means clustering algorithm: analysis and implementation. IEEE Trans Pattern Anal Mach Intell. 2002; 24(7):881–892.

13. Couprie C, Grady L, Najman L, Talbot H. Power watershed: a unifying graph-based optimization framework. IEEE Trans Pattern Anal Mach Intell. 2011; 33(7):1384–1399.

14. Gonzalez RC, Woods RE, Eddins SL. Digital image processing using MATLAB. Upper Saddle River (NJ): Person Prentice Hall;2004.
15. Rudin LI, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms. Physica D. 1992; 60(1):259–268.

16. Perona P, Malik J. Scale-space and edge detection using anisotropic diffusion. IEEE Trans Pattern Anal Mach Intell. 1990; 12(7):629–639.

17. Sinop AK, Grady L. A seeded image segmentation framework unifying graph cuts and random walker which yields a new algorithm. In : Proceedings of 2007 IEEE 11th International Conference on Computer Vision; 2007 Oct 14-21; Rio de Janeiro, Brazil. p. 1–8.
18. Lorensen WE, Cline HE. Marching cubes: a high resolution 3D surface construction algorithm. ACM SIGGRAPH Comput Graph. 1987; 21(4):163–169.

19. Zijdenbos AP, Dawant BM, Margolin RA, Palmer AC. Morphometric analysis of white matter lesions in MR images: method and validation. IEEE Trans Med Imaging. 1994; 13(4):716–724.

20. Chan TF, Vese LA. Active contours without edges. IEEE Trans Image Process. 2001; 10(2):266–277.

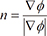 . When ϕ(x,t = 0) is given, the evolution equation for ϕ can be derived as
. When ϕ(x,t = 0) is given, the evolution equation for ϕ can be derived as
 , the curvature K is calculated as the divergence of the unit normal vector:
, the curvature K is calculated as the divergence of the unit normal vector:




 PDF
PDF ePub
ePub Citation
Citation Print
Print


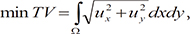
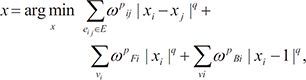

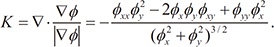


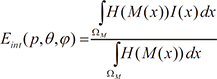



 XML Download
XML Download