2. SVR-based prediction model
Regression is a statistical method which is widely used to predict and analyze the relationship of data between a dependent variable and one or more independent variables. Many kinds of regression methods have been proposed and these can be classified as simple regression and multiple regressions according to the number of independent variables. Regression model can be represented as a function f which is related dependent variable Y.
where X is independent variables and β is unknown parameters.
To estimate appropriate regression model, it is recommended to perform regression with large amount data after eliminating outliers by using standardized residual or studentized residual, because the conventional regression models are extremely influenced by amount and quality of data as shown in
Figure 1.
However to collect large amount with high quality of data is limited, especially, in clinical cases, and outlier is recognized as important object which contains useful information. Therefore, in this study, SVR-based method, which is possible to analyze small amount of clinical data with outliers effectively, is proposed to overcome the drawbacks of the conventional statistical analysis methods.
SVR is constructing regression model by minimizing generalization error based on SRM while other statistical methods are based on ERM [
14]. Moreover SVR performs data analysis in high dimensional feature space which is mapped by kernel function such as polynomial, RBF, and etc. Therefore SVR is possible to deal with small amount of data with outliers.
Suppose the given training data {(xi, yi),⃛,(xN, yN)}⊂χ × R, where N denotes number of data, x, y denote input and output vector respectively, and χ denotes input data space. The goal of SVR is to find a function f that has minimum ω less than ε deviation from the target yi.
where <·,·> denotes the dot product in χ.
Convex optimization problem to find minimum ω can be rewritten as follows.
However, from the Equation (3), it is impossible to analyze the training data that exists out of the bound ε. Therefore, to overcome it, slack variables ξi, ξi* are applied, then Equation (3) can be rewritten as follows.
In here, regularization constant C > 0 controls model complexity by determining how much of error will be allowed for training data that is out of the bound ε.
By applying Lagrange function to solve Equation (4) and kernel function to map data into high dimensional space, it can be rewritten as Equation (5) and (6) [
13-
15].
where k (x, x') := <Φ (x), Φ (x')> and Φ denote mapping function and k denotes kernel function.
Typical kernel functions and their parameters are summarized in
Table 2.
The performance of SVR is closely related to SVR parameters and kernel function. The examples for SVR parameters (C: regularization constant, ε: error bound) are shown in
Figure 2.
From
Figure 2A and 2B, SVR parameter C is related to the complexity of model. That is, the complexity of regression model is increased as C is increased. Therefore, we could compose a model which has minimum training error by selecting higher value of C. However, testing error will be increased with higher value of C, because of overfitting problem.
Moreover
Figure 2C and 2D show the influence of SVR parameter ε. ε controls model complexity similar with C. The difference of C and ε is that C controls complexity by adjusting the error sensitivity of training data, and ε controls complexity by adjusting the number of support vectors. As shown in
Figure 2C and 2D, the number of support vector is decreased and the regression model is simplified as ε is increased.
Therefore, to select optimal parameter is important to construct proper regression model based on SVR. In this study, we have tested on several conditions (C: 500 and 1,000; ε : 0.001 and 0.005; and Gaussian RBF kernel parameter: 2 and 4). According to the condition, we have constructed SVR prediction model to analyze the change of mass diameter on CMT.
To analyze the change of mass diameter on CMT, we have collected data of fifty nine infants with CMT. From the CMT data, we select independent variables based on t-test and Pearson's correlation coefficient. After selecting independent variables, we constructed SVR prediction model using Gaussian RBF kernel. The algorithm of this study is summarized as follows.
Step 1] Collect data of infants with CMT.
Step 2] Select independent variables using t-test and Pearson's correlation coefficient method.
Step 3] Construct SVR prediction model according to SVR parameters.
Step 4] Evaluate the performance of SVR model according to parameters based on root mean square error (RMSE).
The architecture of SVR is shown in
Figure 3.

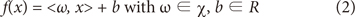
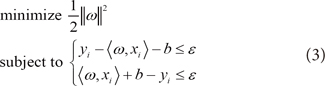
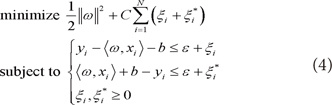
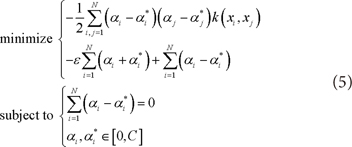
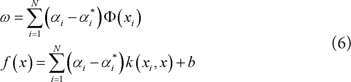




 PDF
PDF ePub
ePub Citation
Citation Print
Print








 XML Download
XML Download