Abstract
Purpose
The management of metal-induced field inhomogeneities is one of the major concerns of distortion-free magnetic resonance images near metallic implants. The recently proposed method called “Slice Encoding for Metal Artifact Correction (SEMAC)” is an effective spin echo pulse sequence of magnetic resonance imaging (MRI) near metallic implants. However, as SEMAC uses the noisy resolved data elements, SEMAC images can have a major problem for improving the signal-to-noise ratio (SNR) without compromising the correction of metal artifacts. To address that issue, this paper presents a novel reconstruction technique for providing an improvement of the SNR in SEMAC images without sacrificing the correction of metal artifacts.
Materials and Methods
Low-rank approximation in each coil image is first performed to suppress the noise in the slice direction, because the signal is highly correlated between SEMAC-encoded slices. Secondly, SEMAC images are reconstructed by the best linear unbiased estimator (BLUE), also known as Gauss-Markov or weighted least squares. Noise levels and correlation in the receiver channels are considered for the sake of SNR optimization. To this end, since distorted excitation profiles are sparse, l1 minimization performs well in recovering the sparse distorted excitation profiles and the sparse modeling of our approach offers excellent correction of metal-induced distortions.
Results
Three images reconstructed using SEMAC, SEMAC with the conventional two-step noise reduction, and the proposed image denoising for metal MRI exploiting sparsity and low rank approximation algorithm were compared. The proposed algorithm outperformed two methods and produced 119% SNR better than SEMAC and 89% SNR better than SEMAC with the conventional two-step noise reduction.
Metal-induced field inhomogeneity is one of the major concerns in magnetic resonance imaging (MRI) near metallic implants. For distortion-free MRI with metallic implants, a number of sequence techniques have been reported in the MRI literature to recover artifacts such as signal loss and distortion in the images. To reduce in-plane distortion with metallic implants, view angle tilting (VAT) (1) spin echo sequence uses a gradient on the slice select axis during readout gradient. The selected slice is successfully viewed at an angle that compensates for the distortion during readout gradient. However, VAT leads to the penalty of blurring due to the modulation of the k-space related to the excited profile. In three-dimensional (3D) MRI near metallic implants, multi-acquisition variable-resonance image combination (MAVRIC) (2) minimizes artifacts by limiting the excited bandwidth and then uses multiple resonance frequency offset acquisitions to cover the full spectral range. MAVRIC has good signal-to-noise ratio (SNR), but requires long scan times. Slice encoding for metal artifact correction (SEMAC) (3) corrects severe metal artifacts by employing additional z-phase encoding steps for each excited slice against metal-induced field inhomogeneity and VAT. SEMAC is effective with superior metal artifact reduction. Despite the advantages of metal artifact correction, since noisy resolved pixels are included in image reconstruction, SEMAC suffers from noise amplification.
To solve this problem, SEMAC with noise reduction (4) has been proposed. This method employs a two-step approach (rank-1 approximation along the coil dimension (c) followed by soft thresholding in the slice direction), but does not consider noise correlation of coils and results in a direct tradeoff between image accuracy and denoising. Thus, to further expedite noise reduction in SEMAC, in this work we develop a novel image de-noising algorithm that exploits 1) low-rank approximation using strong correlation of pixels (x-z) in the slice direction (s), 2) best linear unbiased estimator (BLUE) image combination in the coil direction with noise correlation, and 3) recovery of distorted slice profile using the sparsity of signals in the slice direction with orthogonal matching pursuit (OMP).
The proposed method - Image denoising for metal MRI exploiting sparsity and low-rank priors in SEMAC-sequentially optimizes multi-dimensional SEMAC data (x-y-z-coil-slice) fidelity constraints and high sparsity of distorted slice profiles while preserving the SEMAC-resolved data by solving the constrained optimization problems. The resulting algorithm is compared against turbo spin echo (TSE) alone and the conventional two-step approach proposed by Lu et al. (4), to measure the improvement possible from combining these three different sequential processes.
In 3D MRI, the 3D volume can be separately divided into multiple 2D slices in the readout direction. SEMAC rearranges resolved excitation profiles to correct metal-induced distortions acquiring additional z-phase encoding steps in each slice position. Denote the excitation magnetization ρe(x,z), the metal-induced inhomogeneity Δf(x,z), the z-phase encoding steps zn, the nth incremental gradient amplitude Gzn, the VAT-compensation gradients Gs, and each duration tx, ts, Tzn, the measured k-space signal Sn(kx,ks,kzn) with the coil sensitivity C(x,z) at nth z-phase encoding step is given by
where kx=γGxtx, ks=γGsts and kzn=γGznTzn. To satisfy VAT-compensation condition, ts should be identical to tx. VAT suppresses in-plane distortion of metallic implants exploiting a gradient on the slice select axis during readout gradient. From Eq. [1], one of the multiple z-phase encoding steps has its own signal, whereas the others of the different z-phase encoding steps have signal void in the same slice position. Therefore, multiple resolved data elements are required to preserve their own signal and metal-induced artifacts can be corrected via aligning them to their actual voxel location. To correct through-plane distortions with metal-induced field inhomogeneities, SEMAC uses a linear complex sum integrating the resolved excitation profiles in the slice direction. By manipulating all actual signals into place, 3D distortion-free images can finally be acquired. Despite the advantages of metal artifact correction, since noisy resolved pixels are included in image reconstruction, SEMAC suffers from noise amplification. To address that issue, the proposed algorithm allows combining the two most important attributes of SEMAC data characteristics: correlation and sparsity within the resolved excitation profiles.
In SEMAC data acquisition, the measured signal Y can be represented in the vector form as
where F is Fourier transform operator, P is slice profile Images, and w is noise. Figure 1, illustrates fully described multi-dimensional SEMAC data which consist of the readout direction x, the phase encoding direction y, the slice position direction z, the coil direction c and the slice direction s. Searching for low-rank data, c-s dimensional SEMAC data, shown in Figure 2a, can be made. Due to noise correlation of coils, singular values slowly decrease in Figure 2c. Thus, it is not good approach in c-s dimension because there is a direct tradeoff between image accuracy and denoising. However, strong correlation of pixels exists in z-s dimensional SEMAC data for each coil. The pixels in the x-s dimension are arranged into a single vector: Pj=[ℓ(xj,s0),…,ℓ(xj,sn)]H where xj is the jth pixel in the z direction, and sn is the nth pixel in the s direction. Figure 2b illustrates reduced data representation in the z-s dimension. To exploit the correlation of pixels (in xy-z) along the s direction, image pixels in spatiotemporal dimension are rearranged into a single matrix: L=[P0,…,Pm-1]H where the rows of L correspond to the s direction and the columns of L to the z direction. The zeros in the L matrix are removed and the high SNR pixels are shifted to the center, yielding another permuted matrix Lp (Ns × Nz). In Figure 2c, singular values of z-s dimensional data decrease faster than them of c-s dimensional data. The few significant singular values imply that the dataset can be effectively approximated as a low-rank matrix (5). Thus, singular value decomposition of the Lp followed by the low-rank approximation (67) is performed by minimizing the following constrained optimization problem:
where F is a Fourier transformation operator and Y is the measured data. With the nuclear norm (8), Eq. [3] is replaced as
Since the cost function is strictly convex, it is easy to show that it exists a unique minimum value. Consequently, L̆ matrix means the recovery of low-rank L̆ matrix.
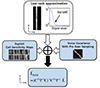
Generally, BLUE (9) is an effective inverse problem method. BLUE is also called SENSE (sensitivity encoding) (10) which is an image-based reconstruction method in parallel MRI (pMRI) (11). Once noises are pre-processed in the xyz-s dimension, SEMAC data is optimally combined in the coil direction using BLUE with noise covariance of coils. The Gauss-Markov theorem states BLUE is defined as
where Ψ is the noise covariance matrix, C is the coil sensitivity, and L̆ is the solution of the optimization problem in the low-rank approximation. In Eq. [5], Ψ is the noise covariance matrix means the levels and correlation of noise from the phase-array receiver channels to optimize SNR. BLUE exploits the noise covariance matrix to de-correlate noise. Figure 3 describes BLUE processing pipeline. Thus, given the explicit knowledge of noise covariance and coil sensitivity from the pre-scan, BLUE reconstruction enhances noise performance in the coil direction. L̆BLUE stands for the high-SNR image sequentially suppressed both noise along z-s dimension and c-s dimension.
The recent theoretical result indicates that minimizing the l1 norm is optimal and readily recovers the sparse signals in some representation frames. As SEMAC data undergo the initial two pre-processing steps (low-rank approximation followed by BLUE), images are rarely contaminated by noises and highly sparse in the slice direction. That is image signals, which result from metal-induced field inhomogeneities, are disseminated to a limited number of resolved data elements. By solving the following constrained optimization problem:
where L̆BLUE indicates the noise-suppressed SEMAC images, sparse distorted slice profiles in SEMAC are recovered using compressive sensing algorithm (121314).
To enhance sparsity, we apply a sparsifying transform, which is 1D Fourier transform along the z direction, in Eq. [6]. Roughly, sparse recovery algorithms are grouped into greedy-type algorithm (1516) and gradient-type algorithm (17) to minimize l1 norm. The recent research results indicate that a greedy-type algorithm called OMP (1819) is comparable for another algorithm called basis pursuit (BP) (20). BP means a principle of global optimization without any specific algorithm and finds signal representations in over-complete dictionaries by convex optimization. However, OMP is an improved version of matching pursuit (MP). An intrinsic feature of MP is that when stopped after a few steps, it yields an approximation exploiting only a few atoms, which means discrete-time signals of length n. When a collection of waveforms is orthogonal, OMP algorithm performs perfectly. Thus, the l1 minimization is performed using the OMP algorithm: It starts from an “empty model”, builds up a signal model, and picks up an atom at a time, which adds to the signal model the most important new atom. This iterative algorithm is converged until the maximum residual signal in x-f domain reaches the noise level. OMP reliably recovers the distorted excitation profiles in x-f domain. Therefore, the final reconstructed image is acquired by inverse Fourier transform (IFT) along the z direction.
Several experiments are performed qualitatively and quantitatively comparing the proposed algorithm with conventional TSE, SEMAC (3), two step noise reduction (4). To investigate the utility of the proposed algorithm, in vivo knee data is acquired in a volunteer with knee arthroplastics (pedicle screws) using 2D SEMAC imaging at a 1.5 tesla (T) whole-body MR scanner (Magnetom Avanto, Siemens Medical Solutions, Erlangen, Germany). 640 noise samples are acquired separately before actual imaging data acquisition. The imaging parameters are: matrix, 320 x 320; FOV, 22 cm; z-phase encoding steps for SEMAC, 8; thickness, 3 mm; flip angle, 150°; effective TE, 36 ms; TR, 3500 ms; number of slice, 24; and imaging time, 5.7 min. A 8-channel standard knee matrix coil is used for signal reception. The noise covariance matrix is estimated from additional noise scan. An off-line image reconstruction of the proposed algorithm for SEMAC is performed using Matlab programming environment (Math Works Inc., Natick, MA, USA). The free parameters for low rank and sparsity priors are empirically chosen. Each reconstructed image is evaluated qualitatively by comparing differently processing images and quantitatively by computing the peak-SNR (PSNR):
The PSNR are computed from final composite magnitude images. As PSNR does not account for preserving important anatomic region of interest, the zoomed images are used to compare the relative performances of the proposed algorithm for SEMAC.
Figure 4 compares pre-processing knee images using low-rank approximation. First row (a-d) is SEMAC without low-rank approximation. Second row (e-h) is SEMAC with c-s low-rank approximation. Third row (i-l) is SEMAC with z-s low-rank approximation. In slice direction, four images, which are two peripheral (a, e, i, d, h, l), intermediate (b, f, j) and central slices (c, g, k), are selected to evaluate the effect of low-rank approximation. Two peripheral images represent the better effect of z-s low-rank approximation and central images represent the similar signal levels. The noise amplification in Figure 4 relatively decreases as the number of row increases. As expected, z-s low-rank approximation qualitatively outperforms two methods.
To further understand the denoising capabilities of BLUE processing, SNR-optimized coil combination is shown for another SEMAC slice profiles in Figure 5 Peripheral (a, e, d, h), intermediate (b, f) and central slices (c, g), are selected to evaluate the effect of BLUE in slice direction. First row illustrates one of coil images which are applied by z-s low-rank approximation. In Figure 5a, b and d still suffer from noise amplification, while Figure 5c has good noise reduction. However, Figure 5c doesn't have enough signal intensity. In contrast, the images of second row are rarely contaminated by noise and image details are returned back. Roughly, e, f and h in Figure 5 have similar signal intensities while Figure 5g has both good noise reduction and signal levels. They also have equally anatomic structure except distorted excitation region. As a result, BLUE processing is effective to noise suppression and provides signal enhancement. Generally, its performance depends on coil sensitivity information and noise covariance estimation. Thus, if the estimated noise covariance matrix is not available, BLUE processing may still be used to suboptimal results.
As SEMAC data undergo the two pre-processing steps, low-rank approximation followed by BLUE, resulting images are rarely contaminated by noises and highly sparse in the slice direction. Figure 6 illustrates sparse recovery using iterative OMP algorithm. Figure 6a and b are similarly shown but Figure 6c means OMP performs well in recovering the sparse distorted excitation profiles. For OMP, the optimal thresholding value is chosen with the consideration of noise level. The optimal value for thresholding is decreased from central slice to peripheral slice in the slice direction because noise amplification and signal level worsen with the distance of central excitation slice. The magnitude difference image demonstrates that tuning thresholding value is empirically critical in obtaining desirable images.
With linear complex sum, multiple resolved excitation profiles change a composite SEMAC image without metal artifacts. Figure 7 compares four images reconstructed using TSE, SEMAC, SEMAC with two-step noise reduction, and the proposed algorithm. TSE with metallic implants suffers from severe metal artifacts and signal loss near metallic implants makes boundary of tissues near metallic implants ambiguous in Figure 7a. SEMAC corrects metal artifacts but the resulting image still has signal degradation in Figure 7b. To tackle noise amplification, two-step noise reduction is introduced. However, noise is not suppressed enough in Figure 7c and computation time also increases with two-step denoising. Figure 7d shows the proposed SEMAC image obtained from low-rank approximation, BLUE and iterative OMP algorithm. The proposed algorithm corrects severe metal artifacts and outperforms two methods and produces 119% PSNR (23.6 dB) better than SEMAC (10.8 dB) and 89% PSNR better than SEMAC with the conventional two-step noise reduction (12.5 dB).
We successfully demonstrated that the proposed, novel algorithm for SEMAC, if compared with conventional denoising methods, substantially improves SNR and reduces artifacts. The proposed method is highly effective and promising for significant clinical impact in evaluation of millions of patients with metallic implants.
SEMAC has shown effective performance in obtaining MR images near metallic implants with correcting metal-induced distortion. Despite the advantages of metal artifact correction, since noisy resolved pixels are included in image reconstruction, SEMAC suffers from noise amplification and has long scan times depending on the additional z-phase encoding steps. To improve the SNR of SEMAC images, SEMAC with noise reduction (4) employs SVD-based denoising with low-rank approximation in the coil direction and soft-thresholding in the slice direction. However, this two-step approach does not consider noise correlation of coils (Fig. 2c) and results in a direct tradeoff between image accuracy and denoising performance. Although obtaining sparse signal recovery, soft-thresholding in image domain may fail to capture small detail in soft tissues.
In the proposed, global two-step SEMAC denoising process, the BLUE image combination is followed by the low-rank approximation. The sequential order is chosen to effectively employ a noise statistic among receiver coils available prior to imaging while enhancing computational efficiency. Let the BLUE image combination in the coil direction be preceded by the low-rank approximation in the z-slice dimension. Then, the matrix LP, which results from the matrix L for each coil using image support reduction and monotonic sorting of voxels, varies coil-by-coil. Since the low-rank approximation operates in the matrix LP, image voxels may experience different denoising in each coil, potentially changing noise correlation among receiver coils.
Hence, the BLUE, which exploits noise covariance among receiver coils as prior information, may produce non-optimal image combination in the coil direction. Additionally, given the reversed order of the global, two-step denoising operation, the low-rank approximation needs to be further applied by a factor of the number of coils, substantially decreasing computational.
To further expedite noise reduction in SEMAC, we propose three-step sequential denoising exploiting low-rank approximation and sparsity in multi-dimensional data representation. The proposed algorithm for SEMAC z-s dimension reduces noise amplification by obtaining the significant singular values using coil sensitivity and noise covariance matrix. Thus, BLUE provides SNR-optimized coil combination. These noise pre-processing steps enable the l1 minimization to recover sparse distorted slice profiles and suppress noise from the correction of through-plane distortions. For rapid imaging, the proposed method is easily combined with fast sampling schemes (1114).
Figures and Tables
Fig. 1
Fully described multi-dimensional SEMAC (slice encoding for metal artifact correction) data representation.

Fig. 2
(a) Reduced data representation in the c-s dimension, (b) reduced data representation in the z-s dimension, (c) normalized singular values of (a) and (b).

Fig. 4
Pre-processing of noise using low-rank approximation. 1st row (no low rank processing): (a) peripheral slice, (b) intermediate, (c) central slice, (d) peripheral slice, 2nd row (c-s low rank processing): (e) peripheral slice, (f) intermediate, (g) central slice, (h) peripheral slice, 3rd row (z-s low rank processing): (i) peripheral slice, (j) intermediate, (k) central slice, (l) peripheral slice.
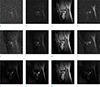
Fig. 5
BLUE (best linear unbiased estimator) processing. 1st row (z-s low-rank): (a) peripheral slice, (b) intermediate, (c) central slice, (d) peripheral slice 2nd row (z-s low-rank + BLUE): (e) peripheral slice, (f) intermediate, (g) central slice, (h) peripheral slice.
References
1. Cho ZH, Kim DJ, Kim YK. Total inhomogeneity correction including chemical shifts and susceptibility by view angle tilting. Med Phys. 1988; 15:7–11.
2. Koch KM, Lorbiecki JE, Hinks RS, King KF. A multispectral three-dimensional acquisition technique for imaging near metal implants. Magn Reson Med. 2009; 61:381–390.
3. Lu W, Pauly KB, Gold GE, Pauly JM, Hargreaves BA. SEMAC: Slice Encoding for Metal Artifact Correction in MRI. Magn Reson Med. 2009; 62:66–76.
4. Lu W, Pauly KB, Gold GE, Pauly JM, Hargreaves BA. Slice encoding for metal artifact correction with noise reduction. Magn Reson Med. 2011; 65:1352–1357.
5. Candes EJ, Recht B. Exact matrix completion via convex optimization. Found Comput Math. 2009; 9:717–772.
6. Cai JF, Candes EJ, Shen Z. A singular value thresholding algorithm for matrix completion. SIAM Journal on Optimization. 2010; 20:1956–1982.
7. Lee K, Bresler Y. ADMiRA: atomic decomposition for minimum rank approximation. IEEE Trans Inf Theory. 2010; 56:4402–4416.
8. Lee K, Bresler Y. Guaranteed minimum rank approximation from linear observations by nuclear norm minimization with ellipsoidal constraint. arXiv preprint. 2009; arXiv:0903.4742.
9. Erez Y, Schechner YY, Adam D. Space variant ultrasound frequency compounding based on noise characteristics. Ultrasound Med Biol. 2008; 34:981–1000.
10. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999; 42:952–962.
11. Blaimer M, Breuer F, Mueller M, Heidemann RM, Griswold MA, Jakob PM. SMASH, SENSE, PILS, GRAPPA: how to choose the optimal method. Top Magn Reson Imaging. 2004; 15:223–236.
12. Donoho DL. Compressed sensing. IEEE Trans Inf Theory. 2006; 52:1289–1306.
13. Daubechies I, Defrise M, De Mol D. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun Pure Appl. 2004; 57:1413–1457.
14. Lustig M, Donoho D, Pauly JM. Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007; 58:1182–1195.
15. Davis G, Mallat S, Avellaneda M. Adaptive greedy approximation. Constr Approx. 1997; 13:57–98.
16. Tropp JA. Greed is good: algorithmic results for sparse approximation. IEEE Trans Inform Theory. 2004; 50:2231–2242.
17. Figueiredo MAT, Nowak RD, Wright SJ. Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems. IEEE J Sel Top Signal Process. 2007; 1:586–597.
18. Tropp JA, Gilbert AC. Signal revocery from random measurements via orthogonal matching pursuit. IEEE Trans Inf Theory. 2007; 53:4655–4666.
19. Gamper U, Boesiger P, Kozerke S. Compressed sensing in dynamic MRI. Magn Reson Med. 2008; 59:365–373.
20. Chen SS, Donoho DL, Saunders MA. Atomic decomposition by basis pursuit. SIAM Review. 2001; 43:129–159.




 PDF
PDF ePub
ePub Citation
Citation Print
Print


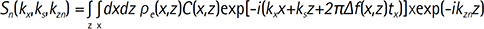
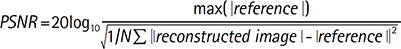


 XML Download
XML Download