Abstract
Purpose
A new compressed sensing technique by iterative truncation of small transformed coefficients (ITSC) is proposed for fast cardiac CINE MRI.
Materials and Methods
The proposed reconstruction is composed of two processes: truncation of the small transformed coefficients in the r-f domain, and restoration of the measured data in the k-t domain. The two processes are sequentially applied iteratively until the reconstructed images converge, with the assumption that the cardiac CINE images are inherently sparse in the r-f domain. A novel sampling strategy to reduce the normalized mean square error of the reconstructed images is proposed.
Results
The technique shows the least normalized mean square error among the four methods under comparison (zero filling, view sharing, k-t FOCUSS, and ITSC). Application of ITSC for multi-slice cardiac CINE imaging was tested with the number of slices of 2 to 8 in a single breath-hold, to demonstrate the clinical usefulness of the technique.
Cardiovascular MRI with high spatial and temporal resolutions is essential to diagnosis; however, the collection of large data within a limited time is challenging, even with the latest high-end hardware (1). Many approaches have been tried to increase the rate of data acquisition with improved hardware, e.g., a high intensity and high slew-rate gradient system (2), and parallel acquisition systems with array coils (3, 4). Fast switching of large gradient fields, however, increases eddy currents and acoustic noise, and induces peripheral nerve stimulation (5, 6). Parallel imaging using the parallel acquisition system has been used for various clinical applications including cardiac MRI to increase the acquisition rate (7).
Alternatively, cardiovascular MRI with less data without much loss of image quality has been investigated, for example view sharing (8), to skip high spatial frequency data or to have different sampling rates for high and low spatial frequency bands, by compromising spatial and temporal resolutions. The skipped data are interpolated (9) or substituted by the measured data at a nearby cardiac phase (10) or simply assumed to be zero. These approaches are relatively easy to implement by software, without adding hardware; however, aliasing artifacts are often observed in the reconstructed images due to the under-sampled data, especially when the compression factor is high (11).
Compressed sensing is another software approach (12). Under-sampling is similarly applied to reduce the rate of data acquisition. However, the sampling locations are random, to reduce aliasing artifacts. Reconstruction with compressed sensing is similar to finding a solution from under-sampled data, with the assumption that cardiac CINE images are sparse in a transformed domain (13). Minimization of the L1 norm is usually applied to find such a sparse solution (14). Minimization of weighted L2 norm iteratively with weighs updated from the currently reconstructed images is tried in k-t FOCUSS (15) and k-t ISD (16) with iterative support detection. Motion estimation techniques in video compression are applied to the reconstruction of compressed sensing (17, 18). Combining the compressed sensing with parallel imaging is introduced to increase the acceleration rate, by merging k-t SPARSE technique with sensitivity encoding (SENSE) (19, 20).
In this paper, a new compressed sensing technique is proposed by iterative truncating small transformed coefficients (ITSC). Unlike most of existing compressed sensing techniques to find the sparest solution among the candidates satisfying the data consistency, ITSC applies the sparseness condition and the consistency condition separately, to make the data sparse by truncating small transformed coefficients in r-f domain first, then the data consistency is applied by restoring the measured data in k-t domain iteratively, until the solution or reconstructed images converge (21). From simulations with in-vivo cardiac CINE MRI data of volunteers, the reconstructed images with various under-sampled data sets converge rapidly, and the normalized mean square errors decrease, as the number of iterations increases. The performance of the ITSC appears superior to existing methods, such as zero filling (1), view sharing (8), and k-t FOCUSS (15). Furthermore the proposed algorithm is computationally efficient and is stable without using matrix inversion during the reconstruction. In-vivo multi-slice cardiac imaging with single breath hold was demonstrated for various compression factors and number of slices for clinical applicability of the technique.
Two-dimensional (2-D) or three-dimensional (3-D) cardiac CINE images have sparse frequency characteristics, due to the periodic motion of the heart with relative small motions between adjacent cardiac frames. If the signal is sparse, a perfect reconstruction may be achieved from under-sampled data (12). The amount of under-sampled or compressed data required for a perfect reconstruction may vary, depending on the sparseness of the data. In cardiac CINE MRI, compression factors (CF) of 2-8 have been reported with reasonable image qualities (3, 13, 16, 17, 18). Since the under-sampling with an equidistance sampling interval introduces aliasing error, a non-equidistance (random) sampling is required for compressed sensing (14).
Figure 1 shows the two test data sets used for the evaluation and optimization of the proposed compressed sensing technique. The data sets were obtained by the balanced steady-state free precession (SSFP) technique from a 1.5 Tesla whole body MRI system, using an eight-channel array coil. Data set A was obtained with the repetition time (TR) and echo time (TE) of 4.71 ms and 2.35 ms, respectively. Data set B was obtained with TR and TE of 4.30 ms and 1.94 ms, respectively. The data from each array coil element was reconstructed separately, and then averaged with magnitude to improve the signal-to-noise ratio. A total of 20 and 16 cardiac frames were contained with temporal resolutions of 37.7 ms and 34.4 ms in the data sets A and B, respectively. Full data were acquired without under-sampling in a single breath-hold. In these experiments, a segmented cardiac sequence was used (22, 23), with the number of views per segment of 8, and the image matrix size of 256x256. Partial echo with an acquisition length of three-quarters of the full echo was acquired in the readout gradient direction, to reduce the echo time for data set B, where the partial echo reconstruction technique is applied with phase correction (24).
Several under-sampled data sets were generated from the fully acquired data sets along the phase encoding gradient direction, which is directly related to the measurement time of the MR examination. For a quantitative evaluation, the normalized mean square error (NMSE) is used, and is given by
Where, Î(x,y;t) denotes reconstructed CINE images from the under-sampled data set, I (x,y;t) denotes reference CINE images obtained from the full data set by conventional 2-D Fourier transform, Nx and Ny the numbers of image matrix sizes in the x and y directions, and Nt the number of cardiac frames. Although two-dimensional CINE images were used, the technique can easily be expanded to three-dimensional CINE images, without loss of generality.
Quantitative evaluations with NMSE are performed for zero filling, view sharing (8), k-t FOCUSS (15), and ITSC. The zero filling method simply assumes zero for the data not acquired. For the evaluation, the technique is assumed to acquire lower spatial frequencies for a given compression factor. Reconstruction is done simply by two-dimensional Fourier transform. The up-sampled image pixels are interpolated by sinc function (25). The view sharing technique acquires data uniformly for a given compression factor. The acquired phase encoding gradients at the current cardiac phase are one step shifted from those at the previous cardiac phase. The data not acquired are adopted or duplicated from the measured data of the same phase encoding gradient at the nearest cardiac phase (8). After filling the data, reconstruction is done by the conventional Fourier transform. The k-t FOCUSS is one of the compressed sensing techniques (15, 17). The technique is known to be a generalized version of k-t BLAST, and shows one of the best performances in the field. Reconstruction is done iteratively to minimize L1 norm by minimizing L2 norm, with updated weighting matrix by the currently reconstructed image for the next stage reconstruction.
Since most of the energy is concentrated in the lower spatial frequency band in general images, including cardiac CINE MRI, a sampling strategy that assigns more acquisitions on a lower spatial frequency band is advantageous, to reduce error due to under-sampling. The sampling strategy is described with a histogram function that is defined as the number of acquisitions for a given phase encoding gradient during a period of the cardiac cycle. Thus the function has the maximum value of the number of cardiac frames, in the case of full acquisitions; and a minimum value of zero, in the case of no acquisition. Three sampling strategies are considered: (a) uniform, (b) Gaussian, and (c) modified Gaussian histogram functions. For the modified Gaussian function, dc is acquired for every frame, and small positive and negative bands are acquired alternatively. For a given number of acquisitions, the acquired frames are chosen randomly, while the total number of acquisitions for each cardiac frame is maintained same. Examples of the acquired frames are shown in the white line segments in Fig. 2 (left) with corresponding histogram functions (right) for CF of 8.
Data sparseness in a transformed domain is a prerequisite to compressed sensing. Since cardiac CINE images are generally not sparse in the spatial domain as a function of time (cardiac phase), some transformations are necessary, to make the transformed coefficients sparse. Several transforms, such as the Fourier transform, discrete cosine transform (DCT), Karhunen Louve transform (KLT) (26), and wavelet transform (13), are known to have an "energy compaction" property, concentrating most of the energy on a small number of transformed coefficients. These transforms have also been widely used for image and video compression (27, 28). Although it's difficult to define data sparseness objectively, independent from reconstruction algorithm, ITSC uses Fourier transform and the data sparseness in r-f domain, following previous explorations in the literature (15, 16). Best results are also obtained using the sparseness of r-f domain in our evaluation with the test data sets. Note that r denotes 2-D or 3-D spatial (image) domain and f denotes frequency obtained by the Fourier transform along the time (cardiac phase).
Reconstruction from under-sampled data in the compressed sensing is similar to finding a solution to the underdetermined equations. In the compressed sensing, the solution (reconstructed image) is assumed to be sparse in the transformed domain. Unlike existing approaches, the sparsity condition is imposed on the currently reconstructed images, by truncating small transformed coefficients in the proposed method. Since the transformed coefficients distributed most sparsely in the r-f domain, the truncation is imposed on the coefficients in the r-f domain. Measured data are, however, restored for data consistency. Thus the key components of the ITSC method are to truncate small transformed coefficients in the r-f domain, and to restore the measured data in the k-t domain iteratively, until the reconstructed images converge. The detailed procedures are described below.
Step 1: Initial estimation of the data not acquired is adopted from the acquired data with the same phase encoding gradient in the nearest cardiac frame. If there are multiple nearest cardiac frames, the average value of the data is used. If there is no measured data for a phase encoding gradient in the entire cardiac cycle, the data is assumed to be zero. This might happen for a high phase encoding gradient with a high compression factor.
Step 2: Using the initial estimation, cardiac CINE images are reconstructed in the r-t space by conventional 2-D Fourier transform.
Step 3: From the reconstructed CINE images, the mean and standard deviation are calculated for each pixel along the cardiac phase. The pixel having a standard deviation below a threshold is classified as a stationary region, and the values in the stationary region are replaced by the mean value for all of the cardiac phase.
Step 4: The CINE images are transformed back to the k-t space by the inverse 2-D Fourier transform, and the measured data are restored for data consistency. Although the restoration may not change the data significantly initially, it is an important step, in conjunction with the truncation of small transformed coefficients.
Step 5: After restoration, the data are reconstructed again, and checked for whether further iteration is necessary. The iteration may be stopped if the reconstructed images converge, i.e., the changes between the currently reconstructed images and the previously reconstructed ones are below a threshold which is determined experimentally. From experiments, the reconstructed images converged rapidly in most cases. In practice, the convergence is well achieved after a predefined number of iterations instead of checking the difference.
Step 6: If further iteration is necessary, one-dimensional Fourier transform is applied along the cardiac phase, to convert the cardiac CINE images into the data in the r-f space. As discussed previously, the data in the r-f space appear most sparse.
Step 7: Small transformed coefficients are truncated below a threshold in the r-f space. A constant or a frequency-dependent threshold function may be used. In our application, a constant threshold is used for all the data in r-f space regardless of the spatial coordinate or frequency. The threshold was chosen by trial and error to make NMSE minimum for the test data sets.
Step 8: The modified data in the r-f space is reconstructed to CINE images. Then the process moves to Step 3 repeatedly.
As seen the procedures, ITSC is a computationally efficient algorithm and is stable without using matrix inversion. The algorithm is adequate for parallel processing, especially with a graphic processing unit (GPU) with massively parallel processors.
The performance of ITSC is evaluated under various conditions, with several under-sampled test data sets. Table 1 shows the normalized mean square error evaluated for the three sampling strategies shown in Fig. 2. In this evaluation, each sampling histogram is optimized to make a minimum NMSE for a given compression factor. For example, the variances of the Gaussian and modified Gaussian histogram functions are optimally chosen to make minimum NMSEs. Table 1 shows that a lower NMSE is obtained with Gaussian or modified Gaussian histogram functions. From Table 1, the sampling histogram function plays an important role in the NMSE of the reconstructed images. The modified Gaussian histogram is chosen for the ITSC method.
Figure 3 shows the convergence of the algorithm tested with NMSE of the reconstructed images as a function of iteration number. This shows that NMSE decreases as the number of iterations increases, although NMSE increases slightly after attaining a minimum point. From experiments, most of the reconstructed images rapidly converge, in a few iterations. Since the reconstructed images with full data are used as reference images, some noise is included in the reference images. Thus there may be some noise effect in the NMSE, especially when the signal-to-noise ratio is not high. A practical way is to apply the algorithms with a predefined number of iterations. From our experience, the number of iterations of 3 or 4 is a reasonable choice.
The performance of the ITSC is evaluated for three under-sampled data sets, with CF of 2, 4, and 8. The performances of three other imaging methods are also evaluated for comparison: zero filling, view sharing, and k-t FOCUSS (15). Figures 4 and 5 show reconstructed images from the test data set A with CF of 2, 4, and 8. Error images by subtracting the reconstructed images from the reference image are also shown, with an amplification factor of 3 for better visualization. Only one cardiac frame is shown out of multiple frames, i.e., a systolic phase in Fig. 4 and a diastolic phase in Fig. 5. As seen in Figs. 4 and 5 all the reconstructed images are very close to the reference image for CF of 2. From the error images (c) k-t FOCUSS and (d) ITSC have less error than (a) zero filling and (b) view sharing. Some blurring and aliasing artifact are found in the reconstructed images with regular sampling (a, b) for CF of 4, while those with random sampling (c, d) show better qualities. Resolution degradation and aliasing artifacts are serious in (a, b) for CF of 8. Although edge sharpness is degraded, better reconstructed images are obtained in (c, d). All the reconstructed images by ITSC, the number of iterations was set 3. Similar results are obtained with the test data set B (see Table 2).
The temporal profiles of the reconstructed images are shown in Fig. 6 for the test set A with CF=4 (top) and for the test set B with CF of 8 (bottom), where the horizontal axis denotes time, and the vertical axis the distance along the phase encoding gradient direction. As seen in the profiles resolution degradation is found in the zero filling (a), edge degradation in view sharing (b). Better profiles are obtained for the compressed sensing (c and d). More detailed profiles are obtained in ITSC method as shown in the white arrows.
Table 2 summarizes the NMSEs of the reconstructed images. Note the performances are dependent on the statistics of the test data sets, e.g., degree of sparseness and signal-to-noise ratio. Table 2 indicates that NMSEs by the compressed sensing techniques (k-t FOCUSS and ITSC) are much lower than those by the zero filling or view sharing techniques. The NMSEs by k-t FOCUSS are similar to those by ITSC. The NMSEs by ITSC are the lowest among the four techniques.
In-vivo multi-slice cardiac CINE imaging is tried by ITSC for real application of the technique. Since full data was not acquired, the quantitative evaluation with NMSE cannot be made. Each row (a ~ e) in Figure 7 corresponds to one cardiac CINE experiment with a single breathhold. For example, the top row corresponds to a single-slice CINE experiment without compression, while the third row corresponds to three-slice cardiac CINE experiment with CF of 3. Locations of slices are chosen similarly to make comparisons between experiments easily. Each slice consists of 16 cardiac frames. Figure 7 shows that reasonable image qualities are obtained, even with a 8-slice experiment (CF=8), which improves diagnosis substantially. Since all the slices are obtained in one experiment in a single breath-hold, they have higher accuracy compared to multiple experiments by changing slice locations without compression, due to limited accuracy in registration of the moving heart with longer measurement time.
The compressed sensing technique tries to make perfect or near perfect reconstruction from under-sampled data, by utilizing sparse distribution of the transformed coefficients. The under-sampling reduces measurement time, while the near perfect reconstruction guarantees diagnostic image quality. A primary question in compressed sensing is whether the transformed coefficients of cardiac CINE MRI are sparsely distributed. The coefficients in a transformed domain have very small magnitudes in most of the high frequencies, and have large values only in a small number of the lower frequencies; thus cardiac CINE MRI may be sparse, if small coefficients are assumed to be zero. The high frequencies, although they are small, contribute to the sharpness of the images in either spatial or temporal domains. Thus some degradation of image quality is inevitable with higher compression factors, and the qualities of the reconstructed images are directly related to the degrees of sparsity of the data.
Reconstruction from under-sampled data is equivalent to finding a solution from underdetermined equations. Thus a priori knowledge is necessary to find such a solution. The solution having a minimum L2 norm is analytically known; however, it is not suitable for cardiac CINE MRI, since the reconstructed images do not usually show sharp edges. The solution having minimum L0 norm (minimum number of nonzero coefficients) agrees well with the definition of sparseness; however, it is difficult to obtain even numerically. The solution having a minimum L1 norm may be the next best choice in most cases.
Unlike existing approaches to find a solution with minimum L1 norm, data sparseness is imposed on the solution, without interference with the measured data. Initial estimation of the solution in ITSC is similar to the view sharing technique, by sharing measured data in near frames. Good initial estimation makes the solution converge rapidly. Data sparseness is imposed by truncating small transformed coefficients in the r-f domain, while the measured data in the k-t space are restored. As truncation and restoration are applied iteratively, the reconstructed images converge to a desirable solution that has sparse distribution in the transformed domain. Since the data in the transformed domain are only approximately sparse, there are limitations in perfect reconstruction, which restricts application of the compressed sensing with high compression factors. From our study, compression factors of 3-4 are reasonable choices for most cases.
The compressed sensing technique may be an inevitable choice to find an optimal solution under various technical constraints (i.e., gradient system, SNR, etc.), and physiological constraints (peripheral nerve stimulation). The technique is often compared to video and image compression. International standards, such as MPEG and JPEG, are widely used in communication and broadcasting. Since full image or video data are available at the encoding end, encoding can be done more effectively. On the other hand, full data are not available in compressed sensing; thus the performance is limited. The main issue in compressed sensing is effective measurement and reconstruction, rather than encoding and decoding. The level of error tolerance in medical imaging may be different from those in broadcasting and multimedia applications. However, there are similarities in utilizing data sparseness; compressed sensing utilizes data sparseness during data acquisition and reconstruction, while video compression utilizes data sparseness during the encoding and decoding processes. There have been many ongoing discussions on to what degree compression factors are permissible for clinical applications (29) and (30). The popularity of MP3, JPEG and MPEG in modern multimedia archiving and communication and broadcasting fields suggests a prospective future for compressed sensing techniques in cardiac MRI.
In conclusion, the proposed iterative truncation of small transformed coefficients method was successfully applied to multi-slice cardiac CINE MRI in a single breath-hold. To obtain 2-8 slices of CINE images using the method improves the diagnosis substantially with corresponding compression factor of 2-8 (same as the acquired number of slices).
Figures and Tables
 | Fig. 1Test data sets for cardiac CINE MRI for evaluation of the compressed sensing technique with other imaging methods. |
 | Fig. 2Three sampling strategies and corresponding sampling locations are exemplary shown for CF of 8: (a) uniform sampling, (b) Gaussian sampling, and (c) modified Gaussian sampling. The acquired locations are shown with white line segments at left, where the horizontal axis denotes the cardiac frame (1~16), and the vertical axis denotes the phase encoding gradient (-128~127). The corresponding histogram functions are shown at right, where the horizontal axis denotes the number of acquisitions over a period of the cardiac cycle, and the c vertical axis denotes the phase encoding gradient. |
 | Fig. 4Reconstructed images at a systolic phase, from the test data set A with CF of 2, 4, and 8 are shown for (a) zero filling, (b) view sharing, (c) k-t FOCUSS, and (d) ITSC. The conventionally reconstructed image with full data is shown at top. Error images are also shown for better visualization. |
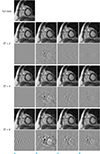 | Fig. 5Reconstructed images at a diastolic phase are shown for (a) zero filling, (b) view sharing, (c) k-t FOCUSS, and (d) ITSC with error images. |
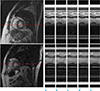 | Fig. 6The temporal profiles of the reconstructed images are shown right, for the test set A with CF of 4 (top) and for the test set B with CF of 8 (bottom).The horizontal axis is time, and the vertical axis is the broken line shown in the reconstructed images left corresponding to the phase encoding gradient direction for (a) reference with full data, (b) zero filling, (c) view sharing, (d) k-t FOCUSS, and (e) ITSC.
|
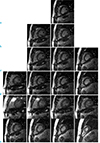 | Fig. 7In-vivo applications of ITSC for multi-slice cardiac CINE MRI.The reconstructed images are shown for (a) without compression, and with CF of (b) 2, (c) 3, (d) 4, and (e) 8. Note the number of slices obtained in single breath-hold is identical to the compression factor.
|
Table 1
The Normalized Mean Square Error is Evaluated for Three Sampling Strategies

Table 2
Summarized NMSEs of the Reconstructed Images with Various Compression Factors

Acknowledgment
This work was supported in part by a National Research Foundation of Korea (NRF) grant, funded by the Korea government (MSIP) (No. 2009-0083512). The present research has also been conducted in part by a Research Grant of Kwangwoon University in 2013, and a Research Grant supported by the Small and Medium Business Administration of Korea.
References
1. Lee VS. Cardiovascular MRI: Physical Principles to Practical Protocols. Lippincott Williams &. Philadelphia: Lippincott Williams & Wilkins;2006.
2. Carpenter TA, Williams EJ. MRI - from basic knowledge to advanced strategies: hardware. Eur Radiol. 1999; 9:1015–1019.
3. Tsao J, Boesiger P, Pruessmann KP. k-t BLAST and k-t SENSE: dynamic MRI with high frame rate exploiting spatiotemporal correlations. Magn Reson Med. 2003; 50:1031–1042.
4. Schmitt M, Potthast A, Sosnovik DE, et al. A 128-channel receive-only cardiac coil for highly accelerated cardiac MRI at 3 Tesla. Magn Reson Med. 2008; 59:1431–1439.
5. Liu F, Zhao H, Crozier S. On the induced electric field gradients in the human body for magnetic stimulation by gradient coils in MRI. IEEE Trans Biomed Eng. 2003; 50:804–815.
6. Glover PM. Interaction of MRI field gradients with the human body. Phys Med Biol. 2009; 54:R99–R115.
7. Schoenberg SO, Dietrich O, Reiser MF. Parallel imaging in clinical MR applications. Berlin: Springer;2007.
8. Riederer SJ, Tasciyan T, Farzaneh F, Lee JN, Wright RC, Herfkens RJ. MR fluoroscopy: technical feasibility. Magn Reson Med. 1988; 8:1–15.
9. Doyle M, Walsh EG, Blackwell GG, Pohost GM. Block regional interpolation scheme for k-Space (BRISK): a rapid cardiac imaging technique. Magn Reson Med. 1995; 33:163–170.
10. Jones RA, Haraldseth O, Müller TB, Rinck PA, Oksendal AN. K-space substitution: a novel dynamic imaging technique. Magn Reson Med. 1993; 29:830–834.
11. Oesterle C, Strohschein R, Köhler M, Schnell M, Hennig J. Benefits and pitfalls of keyhole imaging, especially in first-pass perfusion studies. J Magn Reson Imaging. 2000; 11:312–323.
12. Donoho DL. Compressed sensing. IEEE Trans Inf Theory. 2006; 52:1289–1306.
13. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007; 58:1182–1195.
14. Baraniuk RB. Compressive Sensing. IEEE Sign Proc Mag. 2007; 24:118–124.
15. Jung H, Ye JC, Kim EY. Improved k-t BLAST and k-t SENSE using FOCUSS. Phys Med Biol. 2007; 52:3201–3226.
16. Liang D, DiBella EV, Chen RR, Ying L. k-t ISD: dynamic cardiac MR imaging using compressed sensing with iterative support detection. Magn Reson Med. 2012; 68:41–53.
17. Jung H, Ye JC. Motion estimated and compensated compressed sensing dynamic magnetic resonance imaging: What we can learn from video compression techniques. Int J Imaging Syst Technol. 2010; 20:81–98.
18. Usman M, Atkinson D, Odille F, et al. Motion corrected compressed sensing for free-breathing dynamic cardiac MRI. Magn Reson Med. 2013; 70:504–516.
19. Otazo R, Kim D, Axel L, Sodickson DK. Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI. Magn Reson Med. 2010; 64:767–776.
20. Feng L, Grimm R, Block KT, et al. Golden-angle radial sparse parallel MRI: combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI. Magn Reson Med. 2013; 72:707–717.
21. Ahn CB. A New Compressed Sensing Technique by Iterative Truncation of Small Transformed Coefficients. Proc. ESMRMB. 2012. p. e-Poster 641.
22. Bluemke DA, Boxerman JL, Atalar E, McVeigh ER. Segmented K-space cine breath-hold cardiovascular MR imaging: Part 1. Principles and technique. AJR Am J Roentgenol. 1997; 169:395–340.
23. Park J, Yoon JH, Yang YJ, Ahn CB. Cardiac magnetic resonance imaging using Multi-physiological intelligent trigger system. J Korean Soc Magn Reson Med. 2014; 18:244–252.
24. Margosian P. Faster MR imaging-imaging with half the data. Proc SMR. 1985; 1024–1025.
25. Bernstein MA, King KF, Zhou XJ. Handbook of MRI Pulse Sequences. Amsterdam: Elsevier;2004.
26. Lingala SG, Hu Y, DiBella E, Jacob M. Accelerated dynamic MRI exploiting sparsity and low-rank structure: k-t SLR. IEEE Trans Med Imaging. 2011; 30:1042–1054.
27. Acharya T, Tsai PS. JPEG2000 Standard for Image Compression: Concepts, Algorithms and VLSI Architectures. New Jersey: John Wiley & Sons;2005.
28. Gonzalez RC, Woods RE. Digital Image Processing. 3th ed. New Jersey: Pearson Education;2010.
29. Vasanawala S, Murphy M, Alley M, et al. Practical parallel imaging compressed sensing MRI: Summary of two years of experience in acceleration body MRI of pediatric patients. Proc IEEE Int Symp Biomed Imaging. 2011; 1039–1043.
30. Sharma SD, Fong CL, Tzung BS, Law M, Nayak KS. Clinical image quality assessment of accelerated magnetic resonance neuroimaging using compressed sensing. Invest Radiol. 2013; 48:638–645.




 PDF
PDF ePub
ePub Citation
Citation Print
Print


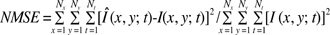

 XML Download
XML Download