Abstract
PURPOSE
The purpose of this study was to develop a dental image processing system using a three-dimensional (3D) camera and stereovision technology. The reliability of the system for measuring axial wall convergence angles was evaluated.
MATERIALS AND METHODS
The new system predicted 3D coordinate points from 2D images and calculated distances and angles between points. Two examiners measured axial wall convergence angles for seven artificial abutments using a traditional tracing-based method (TBM) and the stereovision-based method (SVBM). Five wax abutment models of simplified abutment forms were made and axial wall convergence angles of wax models were measured by both methods. The data were statistically analyzed at the level of significance, 0.05.
Dental clinics often use two-dimensional (2D) photographs for examination of treatment procedures step-by-step or comparison of patient's states between before- and aftertreatment. However, because photographs are 2D representations of three-dimensional (3D) objects, the use of photographs is limited. Using a 3D camera can overcome these limitations. If the 3D coordinates of points from 2D images can be predicted, distances and angles between points can be calculated.
When two cameras are installed on a computer and arranged as the human eye, the two cameras provide different imaging information, that is, caused by so-called disparity like the eyes. Points from the two images can be matched and depth maps (autostereograms) can be created using information about the corresponding points and the baseline separation of the two cameras. The 3D position information of objects can be calculated using this technique.1 Recently, stereoscopic-based methods have been used in various research fields. Dentistry might benefit from this method.
Retention is a long-standing topic of research on fixed dental prosthodontics.2 Several studies have investigated the axial wall inclination to the tooth axis in abutment tooth preparation.3,4,5,6,7,8,9 Typical ways to express axial wall convergence angles are taper and convergence angle. Taper indicates the angle between one axial wall and the long axis of abutment. Convergence angles are the angles between two axial walls.6 As the degree of taper or convergence angle decreases, the retention of a complete veneer crown increases.6,7,10,11 A convergence angle of 4-14° is recommended by many studies.12,13,14 Obtaining the recommended inclination angle when forming an abutment tooth in the oral cavity is difficult because of limitations in accessibility, vision and operator skill.15,16 Clinical research on dental students, intern dentists, and professional dentists shows a clinically acceptable tooth inclination angle of 10-24° which is larger than the theoretically recommended value.5,11,17,18,19,20,21,22
Studies on abutment slope angle have mainly focused on teeth prepared in clinical practice and in vitro experiments on tooth inclination to obtain maximum retention. Measurement methods have not been standardized among different studies. The method most commonly used is a tracing technique, introduced in an initial study.17,19,23,24,25 This method uses an image output or an image magnified with a projector. Convergence angles from the extension lines of abutment teeth are measured wi th a protractor. Conventional methods of measuring 3D objects based on 2D projected images can distort the angle of 3D surfaces. Thus, values can differ among measurers, giving the method a low reliability. The purpose of this study was to develop a new dental image processing system using a 3D camera and to evaluate the reliability of the system by using it for axial wall convergence angle measurements.
A stereovision-based dental image processing system using a stereo camera (Bumblebee2, Pointgrey, Richmond, Canada), notebook computer (E210, LG electronics, Seoul, Korea) and C++ programming (Visual Studio 2010, Microsoft, Seattle, WA, USA) was developed. The system was designed to take photographs of a prepared tooth and show relative and absolute coordinates, length and angulation, degree of enlargement, and information about the translation pixels assigned to the tooth. A 3D coordinate window allows the operator to measure the slope angle of the abutment tooth by taking points and drawing lines.
The image processing flow and a diagram showing the principle of the 3D image mounted on the stereo system are in Fig. 1. Each image was obtained from two cameras. A point on the right image was selected and the corresponding points from the left image were found. Disparity was calculated between two points and a disparity map created. Distance on Z-axis using the disparity was calculated and a depth map created. The 3D coordinates of each point were calculated to generate a depth map.1
Examiners measured the axial wall convergence angles for artificial abutments using the stereovision-based image processing system. The measured axial wall was photographed using the camera and four lines were drawn on the captured image. The four lines were converted into four vectors and the angles between each vector and the XY plane were calculated (Fig. 2). The taper of the axial wall was the arithmetic mean of the four calculated angles (Bucco-palatal convergence angle = buccal taper + palatal taper, mesio-distal convergence angle = mesial taper + distal taper).
Right maxillary second molars that were made of resin (Nissin Dental Product Inc., Kyoto, Japan) were used in this study. These artificial teeth were prepared by students from the Seoul National University School of Dentistry. A dental model (D85S-TRM.406, Nissin Dental Product Inc., Kyoto, Japan) was mounted on a phantom jaw (Shinhung Co., Ltd., Seoul, Korea) and abutments were prepared. Seven abutments were selected from the collected abutments.
Two examiners measured axial wall convergence angles for the seven artificial abutments using the tracing-based method (TBM); two examiners took photographs of the mesial and distal surfaces with a digital camera (IXY 600, Cannon Inc., Tokyo, Japan). The pictures were printed on A4-sized paper, and the printed image size was 1.4 times the actual size. The TBM for measuring the cervical one-third of the axial wall convergence angle used a protractor after tracing. This test was repeated three times.
Two examiners measured axial wall convergence angles for same artificial abutments using the stereovision-based method (SVBM) described above. Tests were also repeated three times.
To assess the accuracy of measurement methods used to determine the value of angles, five wax abutment models in simplified abutment forms were made (Fig. 3). The models were designed to get angles that were designated as true values in this study. The buccal walls of wax abutment models were divided in half to give two kinds of convergence angles (Fig. 3, Table 1).
Two examiners measured axial wall convergence angles for five wax abutment models using the TBM. Pictures of mesial surfaces were taken with a digital camera (IXY 600, Cannon Inc., Tokyo, Japan). As above, tests were repeated three times, pictures were printed to images 1.4 times actual size and a TBM for measuring the axial wall convergence angle used a protractor after tracing. Examiners measured axial wall convergence angles for the same wax abutment models using the SVBM. Tests were repeated three times.
Intraclass correlation coefficient (ICC) was used to assess intra- and inter-examiner reliabilities.26,27,28,29 A 2D mixed model was used and 95% confidence intervals were determined. Bland-Altman plots were used to determine differences in graphs between TBMs and SVBMs versus the mean of the results of the two methods. Paired t-test was used to determine the significance of differences between tracing- and the stereovision-based measurements, and between the bucco-palatal and mesio-distal convergence angles.
The method that gave the values closest to true values was determined. Paired t-tests compared measured angles with true angle values. Statistical operations were performed using PASW Statistics 21 (IBM Co., Armonk, NY, USA) with 95% reliability.
ICC was used to assess intra-examiner reliability (Table 2). ICC values for examiners measuring mesio-distal axial wall convergence angles using the TBM were 0.902 (95% confidence interval: 0.691 < ICC < 0.981) for examiner 1 and 0.923 (95% confidence interval: 0.750 < ICC < 0.985) for examiner 2. For mesio-distal axial wall convergence angles using the SVBM, ICC was 0.925 (95% confidence interval: 0.755 < ICC < 0.986) for examiner 1 and 0.924 (95% confidence interval: 0.751 < ICC < 0.985) for examiner 2. For bucco-palatal axial wall convergence angles using the TBM, ICCs were 0.880 (95% confidence interval: 0.633 < ICC < 0.976) for examiner 1 and 0.885 (95% confidence interval: 0.645 < ICC < 0.977) for examiner 2. For bucco-palatal axial wall convergence angles using the SVBM, ICCs were 0.882 (95% confidence interval: 0.639 < ICC < 0.978) for examiner 1, and 0.887 (95% confidence interval: 0.651 < ICC < 0.978) for examiner 2. Reliability was higher than 0.8 in all cases. For the assessment of inter-examiner reliabilities, the ICC analysis also showed that reliability was higher than 0.8 in all cases (Table 3).
Bland-Altman plots were used to determine differences in graphs between TBMs and SVBMs versus the mean of results for the two methods (Fig. 4). For mesio-distal axial wall convergence angles, the average difference between the tracing-based and stereovision-based measurements was 2.2° and the mean difference ± 2 standard deviations was -12.0° - +16.5°. For bucco-palatal axial wall convergence angles, the average difference between values from the tracing-based and stereovision-based measurements was 6.1° and the mean difference ± 2 standard deviations was -1.8° - +14.1°. A paired t-test was used to determine if differences between the tracing-based and the stereovision-based measurements for artificial abutments were significant. For mesio-distal axial wall convergence angles of artificial abutments, the average difference between the tracing-based and the stereovision-based measurements was 2.2° with standard deviation 7.1° and this difference between the two measurements was significant (P=.048). For bucco-palatal axial wall convergence angles of artificial abutments, the average difference between the tracing-based and stereovision-based measurements was significant at -6.0° with standard deviation 4.0° (P=.000).
A paired t-test was used to determine the significance of differences between bucco-palatal and mesio-distal convergence angle measurements of artificial abutments. The TBM to measure mesio-distal axial wall convergence angles of artificial abutments gave an average difference between mesio-distal and the bucco-palatal axial wall convergence angles of 2.9° with standard deviation 7.1°. The difference between the mesio-distal and the bucco-palatal axial wall convergence angle measurements was significant (P=.010). However, the SVBM gave mesio-distal axial wall convergence angles with an average difference between the mesiodistal and the bucco-palatal axial wall convergence angles of -1.0° with standard deviation 8.1°, which was not a significant difference (P=.441).
The TBM and the SVBM were analyzed for ability to determine true angle values. Paired t-tests compared measured angles with true angle values. For bucco-palatal axial wall convergence angles of wax abutment models, the mean difference between tracing-based measurements and true values was 4.9° with standard deviation 3.3°. The difference between the tracing-based measurements and true values was significant (P=.000). However, for bucco-palatal axial wall convergence angles of wax abutment models, the average difference between stereovision-based measurements and true values was 0.1° with standard deviation was 2.1°, and differences between stereovision-based measurements and true values were not significant (P=.981).
Axial wall convergence angles generally have a wide range because dentists prepare teeth in multiple planes and the dental hand-piece and cutting tools may also introduce variation. Therefore, three-dimensional shape information is needed to indicate the axial wall convergence angle. TBMs use the 3D contours of the wall orthogonal to a 2D plane, resulting in a loss of 3D information.
Our analysis determined inter-examiner and intra-examiner reliability of tracing-based and stereovision-based measurements, giving ICC values between 0.8 and 1.0. Therefore, both methods could be categorized as perfect agreement.30 The two methods were assumed to be reliable since one examiner performing multiple measurements could obtain similar results and different users acquired comparable measurement values. In this study, the cervical one-third of an abutment was measured and measuring criteria were defined according to a study by Kaufman.2
We determined which measurement method acquired angle information that was closest to actual values. For this reason, a wax abutment tooth model with a known tilt angle was fabricated for determining method validity. The TBM showed a significant difference between the actual inclination angle and the measured angle. No significant difference was found between the actual inclination angle and the angle value measured by the SVBM. Therefore, based on the results from this study, a method based on stereovision might provide inclination angles that are more accurate than angles obtained using a TBM.
The slope of an abutment tooth does not generally have a consistent inclination angle across the entire slope. A single tooth slope can have a wide range of tilt angles. Three-dimensional shape information of the slope is required to review inclinations with various values, depending on the site and to apply this information, conversion into numerical data from 3D visual information is required. The mean value of angular information at all points on the slope can be used as a representative value indicating the tilt angle of the slope. Measured values using a conventional TBM do not give accurate representative values. In the TBM, the slope of a 3D tooth shape is orthogonally projected onto a 2D plane. This process loses information about the 3D slope from the projected configuration.
To overcome these limitations, points constituting the 3D surface of the slope must be acquired as coordinated information. The inclination angle at all points on the slope and the average of the convergence angle can be calculated. As technology develops, this method, which a laser scanner currently uses, will improve through active 3D modeling. However, measuring moving objects is difficult, especially when used in open space. In this study, a system was developed using the technology of stereo-based passive 3D modeling. This system has advantages for measuring dynamic objects and can be used in open spaces such as the oral cavity. The SVBM was considered to be a useful tool for tooth preparation in dental clinics, which could be clinically applied to check quickly and to maintain the convergence angle adequately during the abutment preparation procedure.
A dental image processing system using a 3D camera and stereovision technology was developed. The system was used to measure axial wall convergence angles of prepared teeth. Both intra-examiner and inter-examiner reliabilities were excellent for the SVBM and the traditional TBM. The stereovision-based measurement might overcome errors that result from the limitations of 2D methods that measure convergence angles from only a single cross-sectional image of a solid body. The results of this study indicated that the SVBM might provide more accurate values than a TBM. This study also provided an example of how 3D computer science can be applied to clinical dentistry.
Figures and Tables
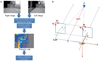 | Fig. 1(A) Image processing flow. Depth or 3D coordinates were calculated from disparity between images from right and left cameras. (B) Schematic diagram showing calculation of depth is calculated from disparities. If the image planes of two cameras are assumed to be on the same plane, and two optical axis are parallel, the focal lengths (f) of the camera lenses are the same (f = f_r = f_l). Point P in the real world can be detected as P_r and P_l in the right and left images. The disparity of two corresponding points P_r and P_l was the difference of the x-coordinate of the two points (disparity = XlP_l - XrP_r). The distance between cameras and targets was calculated as depth = (f × T)/disparity. |
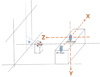 | Fig. 2Angles (α) between each vector and the XY plane were calculated. Four lines on captured two-dimensional images were converted into four vectors (black arrowheads). |
 | Fig. 3Wax abutment model. The buccal wall of the wax model was divided in half, giving two kinds of convergence angles (white arrowheads). |
 | Fig. 4Bland-Altman plots. Mesio-distal convergence angle (A) and bucco-palatal convergence angle (B). Grey lines, average difference of two measurements (stereovision-based - tracing-based). Grey dotted lines, average difference of two measurements ± 2 standard deviations. Especially, note the large difference in bucco-palatal convergence angle, which is considered to show the limitation of 2D analysis for a 3D object. |
Table 1
Wax abutment model sample ID and true value

Table 2
Measurements of axial wall convergence angles in the artificial abutments

Table 3
Inter-examiner reliabilities for the tracing- and the stereovision-based method (n=21)

References
1. Bradski GR, Kaehler A. Learning OpenCV: computer vision with the OpenCV library. Farnham: O'Reilly;2008. p. 555.
2. The glossary of prosthodontic terms. J Prosthet Dent. 2005; 94:10–92.
3. Al-Omari WM, Al-Wahadni AM. Convergence angle, occlusal reduction, and finish line depth of full-crown preparations made by dental students. Quintessence Int. 2004; 35:287–293.
4. el-Ebrashi MK, Craig RG, Peyton FA. Experimental stress analysis of dental restorations IV The concept of parallelism of axial walls. J Prosthet Dent. 1969; 22:346–353.
5. Goodacre CJ, Campagni WV, Aquilino SA. Tooth preparations for complete crowns: an art form based on scientific principles. J Prosthet Dent. 2001; 85:363–376.
6. Jørgensen KD. The relationship between retention and convergence angle in cemented veneer crowns. Acta Odontol Scand. 1955; 13:35–40.
7. Kaufman EG, Coelho DH, Colin L. Factors influencing the retention of cemented gold castings. J Prosthet Dent. 1961; 11:487–502.
8. Weed RM. Determining adequate crown convergence. Tex Dent J. 1980; 98:14–16.
9. Wilson AH Jr, Chan DC. The relationship between preparation convergence and retention of extracoronal retainers. J Prosthodont. 1994; 3:74–78.
10. Lewis RM, Owen MM. A mathematical solution of a problem in full crown construction. J Am Dent Assoc. 1959; 59:943–947.
11. Weed RM, Baez RJ. A method for determining adequate resistance form of complete cast crown preparations. J Prosthet Dent. 1984; 52:330–334.
12. Chandra Shekar S, Giridhar K, Suhas Rao K. An in vitro study to evaluate the retention of complete crowns prepared with five different tapers and luted with two different cements. J Indian Prosthodont Soc. 2010; 10:89–95.
13. el-Ebrashi MK, Craig RG, Peyton FA. Experimental stress analysis of dental restorations. VI. The concept of proximal reduction in compound restorations. J Prosthet Dent. 1969; 22:663–670.
14. Shillingburg HT Jr, Sather DA, Wilson EL Jr, Cain JR, Mitchell DL, Blanco LJ, Kessler JC. Principles of tooth preparations. In : Shillingburg HT, Sather DA, editors. Fundamentals of fixed prosthodontics. 4th ed. Chicago: Quintessence Publishing Co. Ltd.;2012. p. 131–148.
15. Annerstedt A, Engström U, Hansson A, Jansson T, Karlsson S, Liljhagen H, Lindquist E, Rydhammar E, Tyreman-Bandhede M, Svensson P, Wandel U. Axial wall convergence of full veneer crown preparations. Documented for dental students and general practitioners. Acta Odontol Scand. 1996; 54:109–112.
16. Mack PJ. A theoretical and clinical investigation into the taper achieved on crown and inlay preparations. J Oral Rehabil. 1980; 7:255–265.
17. Ayad MF, Maghrabi AA, Rosenstiel SF. Assessment of convergence angles of tooth preparations for complete crowns among dental students. J Dent. 2005; 33:633–638.
18. Dodge WW, Weed RM, Baez RJ, Buchanan RN. The effect of convergence angle on retention and resistance form. Quintessence Int. 1985; 16:191–194.
19. Leempoel PJ, Lemmens PL, Snoek PA, van't Hof MA. The convergence angle of tooth preparations for complete crowns. J Prosthet Dent. 1987; 58:414–416.
20. Ohm E, Silness J. The convergence angle in teeth prepared for artificial crowns. J Oral Rehabil. 1978; 5:371–375.
21. Smith CT, Gary JJ, Conkin JE, Franks HL. Effective taper criterion for the full veneer crown preparation in preclinical prosthodontics. J Prosthodont. 1999; 8:196–200.
22. Velasquez-Plata D, Andres CJ. The art of crown preparation: a review of principles. J Indiana Dent Assoc. 1996; 75:6–11. quiz 12.
23. Kent WA, Shillingburg HT Jr, Duncanson MG Jr. Taper of clinical preparations for cast restorations. Quintessence Int. 1988; 19:339–345.
24. Noonan JE Jr, Goldfogel MH. Convergence of the axial walls of full veneer crown preparations in a dental school environment. J Prosthet Dent. 1991; 66:706–708.
25. Nordlander J, Weir D, Stoffer W, Ochi S. The taper of clinical preparations for fixed prosthodontics. J Prosthet Dent. 1988; 60:148–151.
26. de Vet HC, Terwee CB, Knol DL, Bouter LM. When to use agreement versus reliability measures. J Clin Epidemiol. 2006; 59:1033–1039.
27. Shrout PE, Fleiss JL. Intraclass correlations: uses in assessing rater reliability. Psychol Bull. 1979; 86:420–428.
28. Weir JP. Quantifying test-retest reliability using the intraclass correlation coefficient and the SEM. J Strength Cond Res. 2005; 19:231–240.
29. Doros G, Lew R. Design based on intra-class correlation coefficients. Am J Biostat. 2010; 1:1–8.
30. Landis JR, Koch GG. The measurement of observer agreement for categorical data. Biometrics. 1977; 33:159–174.




 PDF
PDF ePub
ePub Citation
Citation Print
Print



 XML Download
XML Download