INTRODUCTION
MATERIALS AND METHODS
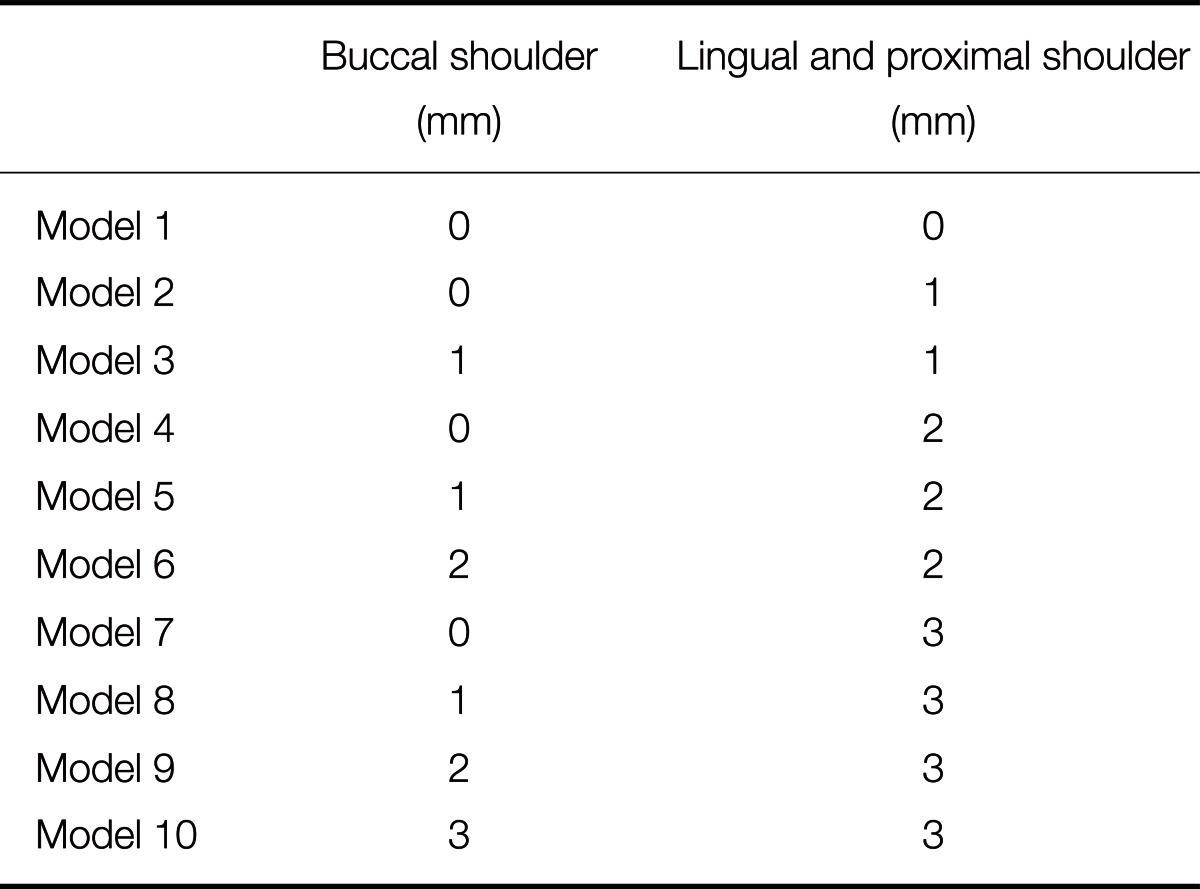
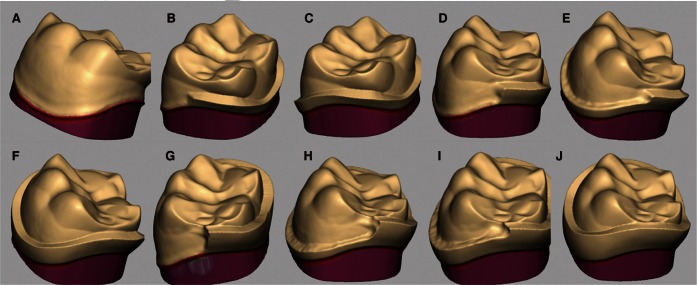 | Fig. 1Schematic representation of the shoulder variations in the zirconia core created in CAD software. The shoulder (1 mm in width) variations in core were incremental increases of 1 mm, 2 mm, and 3 mm in proximal and lingual (PL) height, and buccal (B) height respectively. A: no shoulder, B: PL 1mm, C: PL 1 mm and B 1 mm, D: PL 2 mm, E: PL 2 mm and B 1 mm, F: PL 2 mm and B 2 mm, G: PL 3 mm, H: PL 3 mm and B 1 mm, I: PL 3 mm and B 2 mm and J: PL 3 mm and B 3 mm. |
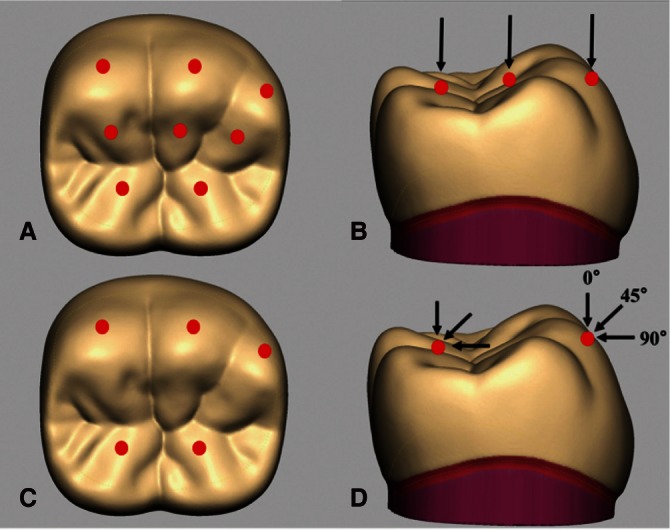 | Fig. 3Loading points and directions simulating maximum bite force (A and B) and masticatory force (C and D). A: Three points on the outer inclines of the buccal cusps, three points on the inner inclines of the buccal cusps, and two points on the inner inclines of the lingual cusps were loaded. B: A total load of 700 N was applied from the axial (vertical) direction. C: Three points on the outer inclines of the buccal cusps and two points on the inner inclines of the lingual cusps were loaded. D: A total load of 280 N was applied from three directions. |
RESULTS
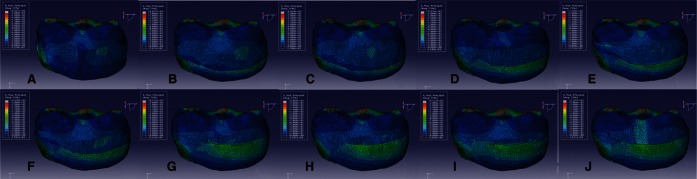
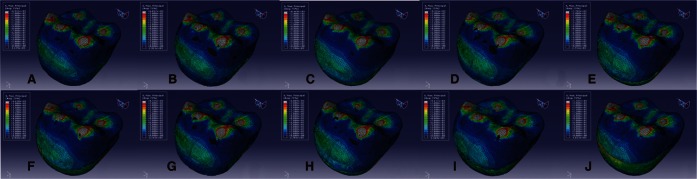 | Fig. 4Maximum principal stress distributions of 10 models subjected to maximum bite force. Maximum principal stress concentrated in the areas around loading points on the crown surface. A: Model 1, B: Model 2, C: Model 3, D: Model 4, E: Model 5, F: Model 6, G: Model 7, H: Model 8, I: Model 9 and J: Model 10. |
 | Fig. 6Maximum principal stress distributions of 10 models subjected to masticatory force (under the application of loads from three directions). (1) load of 280 N at 0° to the to oth axis (vertical direction), (2) load of 280 N at 45° to the tooth axis, towards the lingual margin, and (3) load of 280 N at 90° to the tooth axis, towards the lingual surface (horizontal direction). A: Model 1, B: Model 2, C: Model 3, D: Model 4, E: Model 5, F: Model 6, G: Model 7, H: Model 8, I: Model 9 and J: Model 10. |
 | Fig. 7Lingual side view of maximum principal stress distributions of 10 models subjected to masticatory force. (1) load of 280 N at 0° to the tooth axis (vertical direction), (2) load of 280 N at 45° to the tooth axis, towards the lingual margin, and (3) load of 280 N at 90° to the tooth axis, towards the lingual surface (horizontal direction). A: Model 1, B: Model 2, C: Model 3, B: Model 4, E: Model 5, F: Model 6, G: Model 7, H: Model 8, I: Model 9 and J: Model 10. |
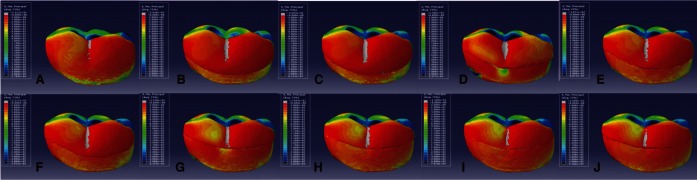 | Fig. 8Lingual side view of minimum principal stress distributions in the 10 models subjected to maximum bite force. A: Model 1, B: Model 2, C: Model 3, D: Model 4, E: Model 5, F: Model 6, G: Model 7, H: Model 8, I: Model 9 and J: Model 10. |
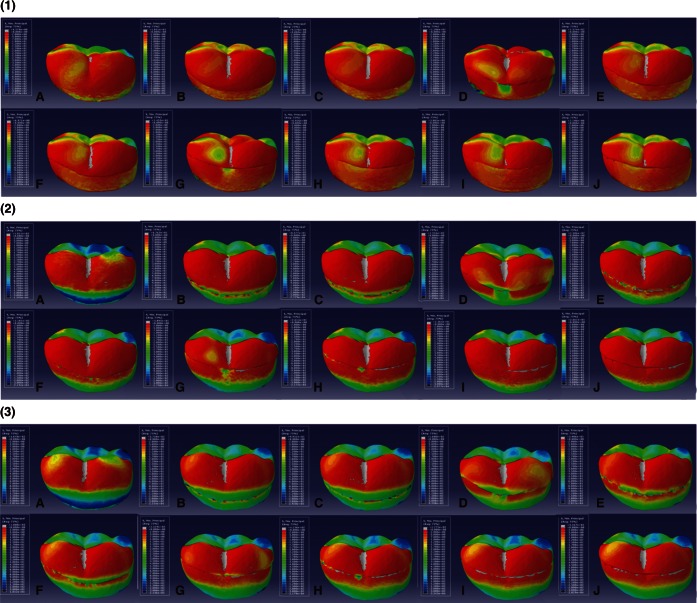 | Fig. 9Lingual side view of minimum principal stress distributions of 10 models subjected to masticatory force (under the application of loads from three directions). (1) load of 28 0 N at 0° to the tooth axis (vertical direction), (2) load of 280 N at 45° to the tooth axis, towards the lingual margin, and (3) load of 280 N at 90° to the tooth axis, towards the lingual surface (horizontal direction). A: Model 1, B: Model 2, C: Model 3, D: Model 4, E: Model 5, F: Model 6, G: Model 7, H: Model 8, I: Model 9 and J: Model 10. |




 PDF
PDF ePub
ePub Citation
Citation Print
Print



 XML Download
XML Download