Abstract
Background
Intra-class correlation coefficients (ICCs) provide a statistical means of testing the reliability. However, their interpretation is not well documented in the orthopedic field. The purpose of this study was to investigate the use of ICCs in the orthopedic literature and to demonstrate pitfalls regarding their use.
Methods
First, orthopedic articles that used ICCs were retrieved from the Pubmed database, and journal demography, ICC models and concurrent statistics used were evaluated. Second, reliability test was performed on three common physical examinations in cerebral palsy, namely, the Thomas test, the Staheli test, and popliteal angle measurement. Thirty patients were assessed by three orthopedic surgeons to explore the statistical methods testing reliability. Third, the factors affecting the ICC values were examined by simulating the data sets based on the physical examination data where the ranges, slopes, and interobserver variability were modified.
Results
Of the 92 orthopedic articles identified, 58 articles (63%) did not clarify the ICC model used, and only 5 articles (5%) described all models, types, and measures. In reliability testing, although the popliteal angle showed a larger mean absolute difference than the Thomas test and the Staheli test, the ICC of popliteal angle was higher, which was believed to be contrary to the context of measurement. In addition, the ICC values were affected by the model, type, and measures used. In simulated data sets, the ICC showed higher values when the range of data sets were larger, the slopes of the data sets were parallel, and the interobserver variability was smaller.
Conclusions
Care should be taken when interpreting the absolute ICC values, i.e., a higher ICC does not necessarily mean less variability because the ICC values can also be affected by various factors. The authors recommend that researchers clarify ICC models used and ICC values are interpreted in the context of measurement.
By definition, reliability means yielding the same or compatible results in different clinical experiments or statistical trials. Reliability is an important concept in medical practice because it can be used to reduce errors during diagnostic evaluations, during the analysis of responses to questionnaires, and even during surgical procedures. Any examination or procedure viewed as reliable would need to produce similar results regardless of time, environment, or examiner.
Various statistical methods can be used to test reliability according to the characteristics of the data (categorical or continuous) and the contexts of testing variables, which include proportion agreement,1) kappa statistics,2) the Phi method,3) Pearson's correlation,4) and intraclass correlation coefficients (ICC).5) Of these, ICC is commonly used to determine the test reliability of continuous variables. It is known to be derived from repeated measures of analysis of variance,6) which produces values that are closest to the formal definition of reliability. In addition, ICCs can be determined for categorical data.7)
However, ICCs can be determined using different models (one way random, two way random, and two way mixed), types (absolute agreement or consistency), and measures (single or average measurements), which can result in different values and confuse researchers wanting to select an appropriate ICC model, type, or measure.5) In addition, ICC values are believed to be sensitive to between-target variability (subject variability) even though they reflect within-target variability (measurements errors) (Fig. 1).5) Subject variability concerns variations from 'true' values in a target population, that is, range of target measurement.
Subject variability can cause unreasonably low or high ICC values when measurement errors are fixed. Furthermore, ICC values convey only statistical information, and could exclude clinical information. The problems outlined above often lead to exaggerated or distorted results, and disparities between statistical results and clinical interpretations.
This study investigated the use of ICCs in the orthopedic literature, to demonstrate the pitfalls of their use in orthopedic physical examinations and the resulting simulated data.
Institutional review board approval was obtained prior to the study.
The first part of this study involved reviewing orthopedic articles that used ICCs and described models, types, and measures used along with article demographics. The second part involved reliability testing on 3 representative physical examinations in cerebral palsy, which were popliteal angle, the Thomas test, and the Staheli test. Three orthopaedic surgeons assessed 30 patients and the interobserver reliability was evaluated using several statistical methods to explore the clinical implication of ICCs. Informed consent was obtained from all patients. Third, simulated data sets were generated from physical examinations using the multivariate normal distribution to demonstrate the effect of the ranges (subject variability) and slopes of the data sets.
In the first part, orthopedic articles that used ICCs for reliability testing were retrieved from the Pubmed database in June 2010 using the following search terms; ("orthopaedic" [All Fields] OR "orthopedic" [MeSH Terms] OR "orthopaedics" [All Fields] OR "orthopedics" [All Fields]) AND intraclass [All Fields] AND correlation [All Fields] AND coefficient [All Fields]. Original articles written in English and categorized as 'orthopedics' in the Thompson Scientific Journal Citation Report database (JCR 2008) were included - review articles were excluded. These articles were reviewed by an orthopedic surgeon. The reviewer determined whether the model, type, and measures of the ICC had been clarified, and classified each article according to the model (one way random, two way random, and two way mixed), type (absolute agreement, or consistency) and measure (single or average measurements). Article demographics included objects of reliability testing and subject numbers were archived, and other concurrent statistical methods for reliability testing were recorded.
In the second part of the study, 3 representative physical examinations (popliteal angle,8) the Thomas test,9) and the Staheli test10)) were performed by 3 orthopedic surgeons (with 10, 9, and 7 years of experience respectively) on the 30 patients with cerebral palsy. The Thomas test and the Staheli test are 2 different methods of measuring hip flexion contracture, whereas popliteal angle is a measure of hamstring tightness. All 3 measurements were expressed in degrees and represented primarily the ranges of motion of hip and knee joints. The physical examinations were based on consensus building, and angles were measured using a standard goniometer. Interobserver reliabilities were analyzed using various statistical methods, which had been used in the orthopedic articles identified in the first part of the study, namely, ICCs, standard errors of measurement (SEM),11) mean absolute differences (MAD),12) and coefficients of variation (CV).13) ICCs were calculated for all possible combinations of model, type, and measure.
Third, a total of 9 data sets were generated based on a multivariate normal distribution. We increased within-group variation by inflating the diagonal term of a covariance matrix, and consequently it resulted in increasing ranges. The off-diagonal terms were modified to affect between-group variation. While a slope of one observer is fixed, slopes of others were gradually increased compared to the reference slope (Fig. 2).14-16)
In order to perform the article review, data description was primarily performed because this study included all possible data rather than a representative sample. For reliability testing of artificial data, ICCs with 95% confidence intervals were assessed with the setting of absolute agreement and single measurement. To determine the interobserver reliabilities of physical examinations, ICCs were calculated using all possible models (one way random, two way random, and two way mixed effect model), type (consistency/absolute agreement), and measure (single/average measurements). SEM, MAD, and CV were calculated for the reliability testing of physical examinations. Means, standard deviations (SD), and ranges of measurements were presented for physical examination data. Data generated by a simulation was obtained from the process of producing a multivariate normal distribution.14-16) Statistical significance was accepted for p < 0.05.
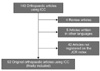
One hundred and forty-three orthopedic articles were found to use ICC for reliability testing. Of these, 4 review articles and 5 articles written in languages other than English were excluded. Of the remaining 134 articles, 42 articles that were not registered in the JCR 2008 were additionally excluded. Finally, 92 original orthopedic articles were found to meet our inclusion and exclusion criteria (Fig. 3). These articles were published between January 1992 and May 2010. Thirty-six (39%) articles primarily evaluated the reliabilities of radiographic measurements, 31 (34%) articles the test-retest reliabilities of a scoring system (questionnaires), 15 (16%) articles physical examinations, and 10 articles the reliabilities of other devices and classifications. The mean number of subjects used for reliability testing in these studies was 71 (SD, 97; median, 40; range, 5 to 610).
Of the 92 articles, 58 (63%) did not clarify the ICC model used in the text. The models, types, and measures used were clearly declared in only 5 (5%) of the articles (Table 1). Concurrent statistical methods used with ICC for reliability test included SEM, MAD, and CV.
In the second part of the study, 30 patients with cerebral palsy (mean age, 12.5 years; SD, 7.7) underwent physical examinations. There were 18 males and 12 females. Of the physical examinations, popliteal angle showed greatest interobserver reliability in terms of ICC values, followed by the Thomas test, and the Staheli test. SEM and CV showed reverse orders in these 3 physical examinations. Mean absolute difference was highest in popliteal angle and smallest in the Thomas test (Table 2). The one way model, absolute agreement, and single measurement yielded lower ICC values than the two way model, consistency, and average measurement.
The simulated data sets showed that the ICC values were affected by the ranges and slopes of the data sets as well as the measurement errors. The ICC of the data sets with smaller interobserver measurement error, wider ranges and parallel slopes showed higher values (Table 3). The fixed model and average measures of the ICC showed higher values than the random effect model and single measures.
A considerable number of original orthopedic articles using ICCs were found not to clarify the models, types, or measures used. The majority of orthopedic articles that used ICCs evaluated the interobserver reliabilities of radiographic measurements, the test-retest reliability of scoring system (questionnaires), and physical examinations. When interobserver measurement errors remained stationary, ICCs increased in line with increasing true subject variability. Reliability testing of physical examination results using several methods revealed that the popliteal angle showed the highest ICC values, followed by the Thomas test, and the Staheli test. However, the mean absolute difference was smallest for the Thomas test, followed by the Staheli test and popliteal angle. Furthermore, the ICC values were affected by ranges and slopes of the data, and differed according to the different models, types and measures.
Before discussing the implications of our results, we need to address the limitations of this study. First, our review of previous orthopedic research that investigated reliability using ICC showed that the majority of articles did not clarify models, types, and measures. These articles might have used ICC appropriately, and the results might have been exaggerated. However, we intended to shed light on the difficulties of interpreting reliability results without information on ICC models, types, and measures, because the ICC values could be dependent on these factors. Second, our article inclusion criteria required an affiliation or author's title with an 'orthopaedic surgery'. However, orthopedic articles sometimes include those produced by other departments than orthopedic surgery, and were excluded from the study. Third, our physical examination data was used for reliability testing purposes, and thus, we remind the reader that this study was designed for research purposes and not for clinical orthopedic purposes.
In interobserver reliability of physical examinations, the one way random effect model, absolute agreement, and single measurement yielded lower ICC values than the two way fixed effect model, consistency, and average measurement. This suggests that ICC values produced during reliability testing could not be interpreted appropriately if the authors do not declare the ICC models, types, and measures used. Furthermore, an appropriate model, type, and measure should be selected based on the context of the investigation envisaged when using ICCs for reliability testing. We believe studies that use ICCs for reliability test need to declare the ICC model, type, and measures used.
During the physical examinations conducted in this study, three orthopaedic surgeons took measurements of 30 patients after consensus building to reduce measurement errors. Of the 4 reliability test methods, only mean absolute difference showed a direct measurement error. We believe that the 3 physical examinations represented similar dimensions (joint range of motion). Even though the mean absolute difference of popliteal angle was larger than the Thomas and the Staheli test results, the ICC value popliteal angle was higher. This means that popliteal angle showed higher ICC values than the Thomas and Staheli tests despite its greater measurement error when evaluating a similar dimension. This disparity between ICC and mean absolute difference showed that ICCs do not always reflect the clinical implications of measurement errors. We believe that it is unreasonable if ICCs used to measure reliability in a similar dimension produces values contrary to the mean absolute difference values. To compensate for this weakness of ICCs, other relevant data or methods representing measurement errors directly, such as, mean absolute difference and categorization at the relevant cut-off values,17,18) might need to be included when reliabilities are investigated using ICCs in orthopedic research. We believe that this would help readers interpret reliability results more comprehensively in terms of their clinical and statistical relevance.
In the simulated data, the ICC values could be affected by factors other than the measurement error itself. Although it is believed that the ICC is the most widely used statistical method for testing the reliability in orthopaedic research and has been found to be useful, there could be pitfalls when using the ICC. Other statistical methods might need to be incorporated when using the ICC and a further investigation will be needed to improve the ICC.
Finally, here we present guidelines for the use of ICCs in orthopedic research: 1) ICCs values can differ and depend on model, type, and the measures used, and therefore, this information should be provided in the text to prevent misinterpretations. 2) ICC values are somewhat sensitive to subject variability, which could lead to different values even for the same measurement errors in similar dimensions. Thus, measurement ranges need to be more clearly presented with ICC values in the reliability tests. 3) ICC values are dedicated to statistical applications, which sometimes make clinical interpretations of ICC values difficult. Other methods evaluating clinical relevance of measurement error should be incorporated into ICC based reliability tests.
Figures and Tables
Fig. 1
Intra-class correlation coefficient (ICC) is defined by the presented formula using between-target mean square (BMS), within-target mean square (WMS), and number of observers (k). BMS represents true subject variability, and WMS represents measurement error.
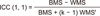
Fig. 2
The data sets were simulated to imitate physical examination situation. We intended to vary the ranges and variability of the data simultaneously. Intra-class correlation coefficient (ICC) is associated with between-group variation and within variation-group. The left lower panel (Data 7) was taken as the reference where means of observers were determined to be 45, 50, and 55 and we increased within-group variation horizontally and between-group variation vertically so that a total of nine data sets were generated based on a multivariate normal distribution. We increased within-group variation by inflating the diagonal term of a covariance matrix, which was shown in horizontal direction and consequently it resulted in increasing ranges. The off-diagonal terms were modified to affect between-group variation. While a slope of one observer is fixed, slopes of others were gradually increased compared to the reference slope and its trend was presented in vertical direction.

Fig. 3
Of the 143 orthopaedic articles using intra-class correlation coefficient (ICC), review articles, articles in other languages than English, and the articles not registered on the Journal Citation Report (JCR) index were excluded. Finally 92 articles were included.
References
1. Kelly MB. A review of the observational data-collection and reliability procedures reported in The Journal of Applied Behavior Analysis. J Appl Behav Anal. 1977. 10(1):97–101.

2. Landis JR, Koch GG. The measurement of observer agreement for categorical data. Biometrics. 1977. 33(1):159–174.

3. Guyatt G, Rennie D. Users' guides to the medical literature: a manual for evidence-based clinical practice. 2002. Chicago: AMA Press.
4. Hunt RJ. Percent agreement, Pearson's correlation, and kappa as measures of inter-examiner reliability. J Dent Res. 1986. 65(2):128–130.

5. Shrout PE, Fleiss JL. Intraclass correlations: uses in assessing rater reliability. Psychol Bull. 1979. 86(2):420–428.

6. Hays WL. Statistics for the social sciences. 1973. New York: Holt, Rinehart and Winston.
7. Fleiss JL, Cohen J. The equivalence of weighted kappa and the intraclass correlation coefficient as measures of reliability. Educ Psychol Meas. 1973. 33(3):613–619.

8. Gage JR, Schwartz MH, Koop SE, Novacheck TF. The identifiation and treatment of gait problems in cerebral palsy. 2009. 2nd ed. London: Mac Keith Press.
9. Thomas HO. Diseases of the hip, knee, and ankle joints, with their deformities, treated by a new and efficient method. 1876. Liverpool: Dobb.
10. Staheli LT. The prone hip extension test: a method of measuring hip flexion deformity. Clin Orthop Relat Res. 1977. (123):12–15.
11. American Education Research Association. American Psychological Association. National Council on Measurement in Education. Standards for educational and psychological testing. 1985. Washington: American Psychological Association.
13. Hendricks WA, Robey KW. The sampling distribution of the coefficient of variation. Ann Math Stat. 1936. 7(3):129–132.

14. R: a language and environment for statistical computing [Interent]. R Development Core Team. 2010. cited 2012 Mar 20. Vienna: R Foundation for Statistical Computing;Available from: http://www.R-project.org/.
15. Genz A, Bretz F, Miwa T, et al. mvtnorm: multivariate normal and t distributions [Internet]. 2012. cited 2012 Mar 20. Vienna: R Foundation;Available from: http://cran.r-project.org/web/packages/mvtnorm/index.html.
16. Revelle W. psych: procedures for psychological, psychometric, and personality research. c2011. cited 2012 Mar 20. Available from: http://personality-project.org/r/psych.manual.pdf.




 PDF
PDF ePub
ePub Citation
Citation Print
Print





 XML Download
XML Download