Abstract
Background
The differential diagnosis of common pigmented skin lesions is important in cosmetic dermatology. The computer aided image analysis would be a potent ancillary diagnostic tool when patients are hesitant to undergo a skin biopsy.
Objective
We investigated the numerical parameters discriminating each pigmented skin lesion from another with statistical significance.
Methods
For each of the five magnified digital images containing clinically diagnosed nevus, lentigo and seborrheic keratosis, a total of 23 parameters describing the morphological, color, texture and topological features were calculated with the aid of a self-developed image analysis software. A novel concept of concentricity was proposed, which represents how closely the color segmentation resembles a concentric circle.
Results
Morphologically, seborrheic keratosis was bigger and spikier than nevus and lentigo. The color histogram revealed that nevus was the darkest and had the widest variation in tone. In the aspect of texture, the surface of the nevus showed the highest contrast and correlation. Finally, the color segmented pattern of the nevus and lentigo was far more concentric than that of seborrheic keratosis.
Skin color is affected by various factors, including melanin, hemoglobin, carotene and thickness of stratum corneum. Pigmented skin lesion (PSL) arises from the abnormalities of those factors1. From the past, PSL has been a great challenge in the field of cosmetic dermatology as well as in basic dermatological research. Although there are numerous reports on the treatment methodology, articles focusing on the image analysis of PSL have been very limitedly published. The diagnosis of PSL usually depends on the ocular inspection of dermatologists.
The advent of high performance computing systems engendered the possibility of handling digital images of megapixels. Not to mention the engineering application, the computer-aided image analysis (CAIA) has been widely accepted in the field of medicine, particularly in radiology2,3. Despite the relative ease of acquiring clinical pictures, the image analysis does not receive sufficient attention from dermatologists. Moreover, most dermatological researches on image analysis are from Western countries. Thus, they primarily explore the properties of melanoma4. In Asia, however, the incidence of melanoma is much lower than that of the west5. Instead, differentiating benign PSLs, such as nevus, lentigo and seborrheic keratosis, from each other is more frequently requested in an every-day clinic. Because Asians usually hesitate to receive invasive procedures on their faces, CAIA could be a potent substitute for a skin biopsy.
We developed a CAIA software in order to collect the characteristic parameters of each PSL. Those variables would not only play significant roles in understanding the characteristics of PSLs, but also give some clues to invent a computer-aided diagnostic system.
The magnified photos of patients' PSL were taken in order to achieve a better diagnostic outcome. A digital magnifier of polarized light source (AM-413TL; Dino-Lite, Hsinchu, Taiwan) has been used to obtain Joint Photographic Experts Group (JPEG) images of 8-bit red, green and blue (RGB) format and 1,280×1,024 pixels. Magnification power of 20 is fixed to every photo taken.
Photos of the commonly acquired melanocytic nevus, common seborrheic keratosis without irritation and senile lentigo were retrospectively retrieved. A highly experienced dermatologist confirmed the clinical diagnosis of each photo. Only focused photos containing the entire PSL, without trim, were included. After quality control, 5 photos were available for each PSL (Fig. 1). This study was approved by the Institutional Review Board of Seoul National Bundang Hospital (B-1203/148-103).
Any artifacts caused by illumination unevenness or humps of the PSLs should be eliminated. Those artifacts were subtracted from the original images by applying the least square method algorithm6. We adopted the first order fitting formula (1), which minimizes the least square (2). In (1), x and y are pixels located in a two-dimensional coordinate system; in addition, a, b and c are coefficients from the least square method. In (2), I(x,y) means the actual intensity of the corresponding pixel.
Through this transformation, the RGB space could be switched to another three-dimensional matrix. This is advantageous because the primary component of the transformed matrix contains more information than any dimensions of the previous RGB space. It enables us to deal with a one-dimensional gray image rather than the three-dimensional RGB, thus making CAIA much faster and more effective7. In fact, the primary component gray image represents the original colored version much better than that of R, G and B (Fig. 2).
To remove the background white noises, the close and open operation utilizing the disc of a five pixel diameter was performed. The open operation eliminates thin lines as well as the isolated pixels, whereas the close operation fills the gaps. This is a commonly used image processing technique for reducing the background white noises8.
The PSLs, located on the scalp, were covered with hair to some degree. The hair made further processing of CAIA difficult. A simple hair detecting filter was implemented, based on the fact that hairs are long, thin and dark strings in a gray image. Due to the fact that ordinary Asians have black hair, we first extracted every pixels of intensity below the threshold value, obtained by Otsu's algorithm. Our threshold should maximize the difference between the two averages from the separated groups, while minimizing each of the intra-group variation. Then, for the pixel group darker than the threshold, we performed a pattern analysis, selecting subgroups of contiguous pixels which are characterized by a high ratio of height to width. The hair mask is applied to the original image and the hair shafts are negated9,10. After subtracting the hairs from the image, the empty pixels were substituted with interpolation using the surrounding pixels.
To detect the proper borders of PSLs from the preprocessed images, we manually selected two pixels representing the points inside the lesion along with four pixels outside the lesion. Our CAIA software primarily generates lesions masked by Otsu's threshold algorithm. Then, it automatically iterates fixing the mask until the mask includes two inside pixels and excludes four outside pixels. If the temporary binary mask includes one of the outside pixels, the threshold is modified to shrink the size of the mask by multiplying the coefficient11. On the contrary, if the mask excludes one of the inside pixels, the mask is expanded by modifying the threshold. The iteration goes on until it finds a mask satisfying the above condition. An example shows the detected borders of each PSL (Fig. 3).
The perimeter and the area are defined as the number of pixels around the boundary and inside the lesion mask, respectively12. To define a perimeter, we adopted an 8-connection method. This method implies that two pixels are said to be contiguous when one is located just left, right, upward and downward of another or at just the next spot in four diagonal directions. The area divided by the square of the perimeter is defined as the roundness.
As a lesion is more similar to a circle, the roundness becomes larger. The solidity is defined as the area divided by the size of a minimum convex mask, which can encircle the entire lesion. Higher solidity stands for being more convex, while a lower solidity implies one that is more spiky and concave.
Each of the RGB space is an 8-bit gray bitmap. Thus, every pixel has an intensity of integer between 0 and 255. The histogram analysis generates several variables, which explain the pattern of the gray level distribution12. If we denote an intensity level to x, p(x) is defined as the probability density of intensity x.
The mean, defined as (5), implicates the average intensity of brightness. The image with a bright tone has a high mean value.
The standard deviation (SD) describes the spread in the intensity. A high contrast image yields high SD.
Texture information is extracted from the co-occurrence matrix. The co-occurrence matrix contains information as to how the nearby pixels are related12,13. This can be calculated in four directions: vertical, horizontal and two diagonals. As the 8-bit bitmap is our concern, the co-occurrence matrix would be 256 by 256 in terms of rows and columns. If we denote the probability density of the i-th row and j-th column as p(i, j), the contrast and correlation is defined as the formulas (8) and (9), respectively.
The µi, µj each means the average of the i-th row and σi, σj j-th column, and as the standard deviation, respectively. The contrast describes the degree of difference between the nearby pixels. An image of high contrast means that its pixels are distinctive from each other; thus, it is more like a rough mosaic rather than a fine gradient. Although it is nearly impossible to notice the subtle difference of the contrasts among the PSLs with the naked eye, the CAIA enabled us to analyze the parameter directly. The correlation describes the linear relationship between the nearby pixels. The correlation is mathematically a complicated notion, but intuitively a simple one. By definition, the correlation implies that the Pearson's coefficient of the two dimensional linear regression between the (x, y) positions in the Cartesian coordinate is the independent variable, and the intensities corresponding to those pixels are the dependent ones. Therefore, an image with a simple linear intensity distribution pattern would have a high correlation value.
K means that the algorithm is a clustering method, which classifies a set of data into K clusters in which each datum is closest to the mean of its cluster14. Mathematically, if we denote a datum to a vector form x, (x1 through xn, for total of n data) and K clusters S, (S1 through Sk, for total of K clusters), the clustering should be done to minimize the sum of within-cluster variances defined by the formula (10).
The µi stands for the mean of the i-th cluster. The operator ║x-y║ calculates the distance between vectors x and y. Among the various methods of defining the distance, the K-mean function of MATLAB® adopts the Euclidean method.
In our analysis, the lesions were divided into four color segments. According to the number of pixels belonging to the minimal convex area completely containing each segment, segment 1 is the smallest and segment 4 is the largest. This allocation means that segment 1 is distributed as the narrowest, while segment 4 is the widest. For pixels belonging to segment 1, only pixels contiguous to each other, in the aspect of the 8-connection method, are redefined into subgroups. Among those subgroups, the ratio between the sizes of the largest subgroup to the size of an entire segment 1 is denoted as the percent area (PA).
The PA describes how well the core is grouped. If the core is one piece, the PA is one. If the core is composed of scattered pixels without direct connections between them, the PA would be zero.
When we denote the minimal convex area which includes the entire pixels of segment 2 as a hull, the ratio of the pixels belong to segment 1, which also belongs to the hull of the entire pixel 1, is defined as the core inclusion (CI).
The CI describes how well the second smallest area encircles the core. If the figure is completely concentric, the second smallest would be the first hull encircling the core. Thus, the CI would be one. However, if the first and the second largest areas are completely separated from each other, the CI becomes zero.
Finally, when we denote the minimal convex area, which includes the entire pixels of segment 1 as a core, the ratio of pixels belonging to segment 2 which does not belong to the core of the entire pixel 2 is defined as the hull exclusion (HE).
The HE describes how exclusively the hull surrounds the core. The HE of a perfect concentric figure is one. However, if the first and second largest areas are intermixed with each other, the HE would be zero. To emphasize the discriminating power of those concentricity properties, the product of the three variables is defined as the concentricity ranging from zero to one. Of course, concentricity closer to one implies a better concentric structure. Actual examples of nevus and seborrheic keratosis are also supplied (Fig. 4).
For each of the five images containing nevus, lentigo and seborrheic keratosis, a total of 23 (four morphologic-, nine color histogram-, six texture- and four topological-) features were used for analysis. With the aid of the Image Processing Tool® library embedded in MATLAB®, the raw jpeg images are loaded to the CAIA software. With minimal manual manipulation of choosing two inside pixels and four outside pixels, the CAIA software automatically performs the preprocessing, border detection and analysis and also provides the numerical outcomes. It also presents graphical data, particularly for the concentricity analysis. The numerical outcomes are analyzed through a non-parametric Kruskal-Wallis test, because only five data were enrolled for each PSL.
It was revealed that the seborrheic keratosis tended to have a larger area and perimeter than that of nevus or lentigo in a morphologic analysis. The roundness and solidity, which both describe the convexity, tended to be larger in the nevus than in the lentigo and in seborrheic keratosis (Table 1).
Three color histogram parameters (mean, SD and entropy) exist in each of R, G and B color space. The mean tended to be lower, while SD and entropy were higher in nevus than in others. Interestingly, it holds truth among all the RGB color space. The SD and entropy would be higher in nevus, since the intensity varies in a wider range in nevus than in others (Table 2).
Each of the two texture parameters (contrast and correlation) in R, G and B color space was analyzed. Both contrast and correlation of nevus tended to be higher than those of others in all RGB (Table 3).
We developed a CAIA software, which is able to detect a border of PSL with minimal supervision. The outcomes of detection were quite acceptable. It also provided several parameters describing the morphological, color, texture and topological features. Nevus was characterized by a dark color and round shape. Lentigo was similar to a nevus, but had a brighter tone and a smaller size. Seborrheic keratosis was larger than the other two. The most interesting finding of our work is that the concentricity was higher in nevus and lentigo than in seborrheic keratosis. The concentricity is a novel notion we introduced, which gives us a clue to hypothesize the difference between the pathogeneses of each PSL. That is, nevus and lentigo come from the dysplasia of melanocytes originating from a point15, whereas seborrheic keratosis originate from multiple simultaneous proliferations of keratinocytes16. The radial growth of melanocytes from the center of dysplasia makes nevus and lentigo have an intensity distribution of concentric pattern, while the multifocal proliferation of much abundant keratinocytes makes seborrheic keratosis have a random pattern.
Due to the fact that only three kinds of benign PSLs were included and five photos were allocated for each PSL, it is hard to generalize the above hypothesis even though this pilot investigation clearly demonstrated the efficiency of CAIA in distinguishing the three benign PSLs from each other. From this point of view, additional studies including more CAIA parameters and more types of PSLs are strongly required. The convergence of technology, clinical dermatology and basic science will bring forth a better understanding of pathogenesis and a higher diagnostic power with the aid of computers.
Figures and Tables
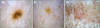 | Fig. 1Raw images of nevus, lentigo and seborrheic keratosis. Magnification power is fixed to 20. (A) Nevus. (B) Senile lentigo. (C) Seborrheic keratosis. |
 | Fig. 2The principal component is more suited for further analysis compared to red (R), green (G) and blue (B). Original image is Fig. 1A. (A) R color space gray image. (B) G color space gray image. (C) B color space gray image. (D) Principal component. |
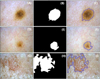 | Fig. 3Border detection and lesion mask creation. Original image, binary mask, and border marked image of (A~C) nevus, (D~F) lentigo, and (G~I) seborrheic keratosis. Border is marked with blue line. |
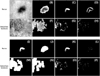 | Fig. 4Color segmented images of nevus and seborrheic keratosis. (A, E) Original gray images of nevus and seborrheic keratosis. (B, F) For nevus, it is well segmented as a concentric pattern through K-means algorithm, K=4. However, the segmented outcome is far from concentric for seborrheic keratosis. (C, G) Segment 1, of which pixels distribute most narrowly. For nevus, the pixels of segment 1 are well aggregated as a single piece. However, the pixels of segment 1 from seborrheic keratosis are relatively separated from each other. (D, H) Segment 2, of which pixels distribute second most narrowly. For nevus, it is a shape of a ring, while for seborrheic keratosis, it is a collection of separated pixel clusters. (I, M) Core, which is defined as the minimal convex area completely encircling segment 1. (J, N) Hull, which is defined as a minimal convex area completely encircling segment 2. (K, O) In the intersection of segment 1 and the hull of nevus, most pixels of segment 1 are located inside of the hull. Thus, the core inclusion (CI) is high (CI=1.0). However, the intersection of segment 1 and core is quite smaller than segment 1 (CI=0.690) for seborrheic keratosis. (L, P) The intersections of segment 2 and core. In the image for nevus, only few pixels of segment 2 overlap with the core. Thus, the hull exclusion (HE) is high (HE=0.952). However, for seborrheic keratosis, most pixels of segment 2 overlap with the core. Thus, HE is lower than that of nevus and lentigo (HE=0.109). |
Table 1
Morphological analysis; mean values of area, perimeter, roundness and solidity of nevus, lentigo and seborrheic keratosis

Table 2
Color histogram analysis; mean values of mean, SD, and entropy of nevus, lentigo and seborrheic keratosis defined in each RGB color space

ACKNOWLEDGMENT
This study was supported by grant from Seoul National University Bundang Hospital, Korea (02-2012-034).
References
2. van Ginneken B, ter Haar Romeny BM, Viergever MA. Computer-aided diagnosis in chest radiography: a survey. IEEE Trans Med Imaging. 2001; 20:1228–1241.

3. van Ginneken B, Schaefer-Prokop CM, Prokop M. Computer-aided diagnosis: how to move from the laboratory to the clinic. Radiology. 2011; 261:719–732.

4. Vestergaard ME, Menzies SW. Automated diagnostic instruments for cutaneous melanoma. Semin Cutan Med Surg. 2008; 27:32–36.

5. Armstrong BK, Kricker A. Cutaneous melanoma. Cancer Surv. 1994; 19-20:219–240.
6. Scherg M, Brinkmann RD. Least-square-fit technique applied to the frequency following potential: a method to determine components, latencies and amplitudes. Scand Audiol Suppl. 1979; (9):197–203.
7. Pribić R. Principal component analysis of Fourier transform infrared and/or circular dichroism spectra of proteins applied in a calibration of protein secondary structure. Anal Biochem. 1994; 223:26–34.

8. Stoffel JC. Graphical and binary image processing and applications. Dedham, MA: Artech House;1982. p. 580.
9. Lee T, Ng V, Gallagher R, Coldman A, McLean D. Dull-Razor: a software approach to hair removal from images. Comput Biol Med. 1997; 27:533–543.

10. Kiani K, Sharafat AR. E-shaver: an improved DullRazor(®) for digitally removing dark and light-colored hairs in dermoscopic images. Comput Biol Med. 2011; 41:139–145.

11. Abbas Q, Celebi ME, Fondón García I, Rashid M. Lesion border detection in dermoscopy images using dynamic programming. Skin Res Technol. 2011; 17:91–100.

12. LeAnder R, Chindam P, Das M, Umbaugh SE. Differentiation of melanoma from benign mimics using the relative-color method. Skin Res Technol. 2010; 16:297–304.

13. Pantic I, Pantic S, Basta-Jovanovic G. Gray level co-occurrence matrix texture analysis of germinal center light zone lymphocyte nuclei: physiology viewpoint with focus on apoptosis. Microsc Microanal. 2012; 18:470–475.

14. Yu S, Tranchevent LC, Liu X, Glänzel W, Suykens JA, De Moor B, et al. Optimized data fusion for kernel k-means clustering. IEEE Trans Pattern Anal Mach Intell. 2012; 34:1031–1039.

15. Happle R. What is a nevus? A proposed definition of a common medical term. Dermatology. 1995; 191:1–5.




 PDF
PDF ePub
ePub Citation
Citation Print
Print



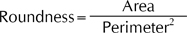
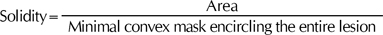
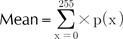
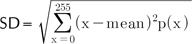
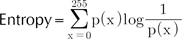
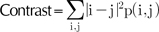
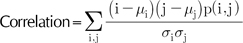
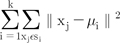

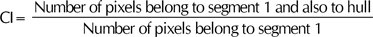



 XML Download
XML Download