PDF
ePub
Citation
Print
서론
대부분 의학연구의 의사결정 과정은 통계학적 방법을 사용한다. "현재 사용하고 있는 당뇨 치료약 A와 B중 어떤 치료약의 효과가 좋은가?"라는 물음을 생각해 보자. 임상 연구자는 위의 의문을 풀기 위해 다양한 방법으로 자료를 수집할 수 있을 것이다. 본 논문은 의학연구에서 빈번히 사용하고 있는 많은 통계적 방법들을 이론 중심으로 설명하기 보다는 가상적 예제의 연구설계나 자료형태를 통해 이들의 관계를 서로 연결하고, 단순한 분석으로부터 복잡한 분석방법까지 어떤 과정을 거쳐 실제 연구자료에 적용할 수 있는지, 임상 연구자 관점과 통계상담자 관점에서 문제를 풀어가는 과정에 초점을 두어 설명하고자 한다.
본 논문에서 다루고자 하는 통계적 의사결정 방법은 의학연구에서 빈번히 사용되고 있는 t-검정, 분산분석(analysis of variance), 여러 가지 비모수적 방법(nonparametric method), 카이제곱 검정(χ2-test), 다중 회귀분석(multiple regression), 로지스틱 회귀분석(logistic regression), 혼합모형(mixed model), 로그-순위 검정(log-rank test), 콕스 회귀모형(Cox regression model) 등이다.
본 논문은 임상연구 상황에 좀 더 가까이 다가가기 위해 가상적으로 임상연구자 Dr. P와 통계상담자 Dr. S를 등장시키고, 대화과정을 통해 임상연구를 수행하면서 느낀 어려움을 풀어가는 방향으로 설명하고자 한다.
통계방법 선택에 대한 가이드라인
Dr. P가 밝히고자 하는 가설은 "현재 사용하고 있는 여러 가지 당뇨병 치료제 중 어떤 치료약의 효과가 좋은가?"이다. 치료의 효과는 다양한 방법으로 측정할 수가 있으며, 다음 치료약의 효과를 어떻게 측정하였는가에 따른 상황별로 여러 가지 분석방법을 생각하고, 이들을 연계, 확장해 보도록 하자.
1. 치료약의 효과를 HbA1c 농도로 측정한 경우
1) 상황 1
Dr. P는 치료약의 효과를 치료 12주 후 HbA1c 농도(%)를 통해 평가하고자 한다. 수집한 자료는 치료제 A를 투여 받은 30명과 치료제 B를 투여 받은 30명이다.
Dr. P는 두 집단에서의 HbA1c의 평균 농도를 각각 구한 다음 이를 비교하는 것이 좋을 것이라 생각하였다. 즉, 만약 두 표본 평균의 차이가 크면 이러한 차이는 두 모집단의 평균에 차이가 있기 때문에 발생한 것으로 생각이 되고, 만약 두 군의 표본 평균의 차이가 작으면 두 모집단의 평균이 같은 상황에서 표본을 뽑는 과정에서 발생할 수 있는 우연한 차이라고 생각할 수 있다. "그럼 두 표본 평균의 차이가 어느 정도 되어야 두 모집단의 평균 차이가 있다고 할 수 있을까?" 이는 통계를 전공으로 하지 않는 사람에게는 참 어려운 질문이다.
(1) Dr. S의 설명
두 모집단에서 각각 동일한 크기의 표본을 뽑아 두 표본 평균의 차이(통계량)를 계산하면 어떨까? 아마 이 값들은 계속 다른 값들이 나올 것이다. 이와 같이 통계량은 표본을 뽑을 때의 표본의 변동성으로 분포를 가지고 있고, 우리는 통계량의 표준편차를 표준오차(standard error)라고 정의한다[1]. 일반적으로 통계적 의사결정에는 위의 예와 같이 두 모집단의 평균 차이를 잘 추측할 수 있는 통계량(두 표본 평균의 차이)을 이의 표준오차로 나눈 형태를 많이 사용한다.
독립된 두 모집단의 평균에 차이가 있는가를 검정할 때 두 표본평균의 차이를 이의 표준오차로 나눈 독립된 두 집단의 t-검정(independent two-sample t-test)을 많이 사용한다. 상황 1에서는 우선적으로 독립된 두 집단의 t-검정을 사용할 수 있다. 한편, 독립된 두 집단의 t-검정 통계량은 두 모집단의 분산이 같은 경우(등분산인 경우)와 다른 경우(이분산인 경우)에 사용하는 검정 통계량의 형태가 다르므로 연구자는 두 모집단의 분산이 같은가를 먼저 검정한 후 이에 따라 적합한 통계량을 선택하여야 한다[1]. 많이 사용하는 통계 프로그램들에서는 모두 이러한 과정들의 결과를 제시하여 주므로 사용하는데 큰 어려움이 없다.
(2) Dr. P의 의문
"만약에 표본 평균이 모집단의 평균을 잘 대표하지 못하는 상황에서 t-test를 사용하는 것은 타당한가?" 아마 많은 관측 값들에 비해 소수의 관측 값들이 매우 큰 값(이상치)이 있는 경우, 표본 평균은 이들 소수 관측 값들의 영향을 크게 받아 모집단의 대푯값 역할을 하는데 무리가 있을 것이고, 또한 표본의 크기가 작을수록 이러한 이상치의 영향은 점점 커질 것이다. 따라서 이러한 상황에서 이상치의 영향을 적게 받는 통계량을 사용하여 의사 결정하는 것이 좋을 것 같다.
(3) Dr. S의 설명
일반적으로 모집단의 분포가 정규분포를 따르는 경우에는 표본 평균을 이용하여 의사 결정하는 것이 좋은 선택(통계적 검정력이 높다는 의미)이다. 모집단의 분포를 가정하고 검정하는 방법을 모수적(parametric) 방법이라 한다. 반면 모집단의 분포가 한쪽으로 치우쳐 이상치가 있거나, 특정한 분포를 가정할 수 없는 경우에는 모집단의 분포를 가정하지 않고 자료의 순위(rank)를 이용하여 의사 결정하는 비모수적 방법이 있다[1].
독립된 두 집단의 t-검정에 대응하는 비모수적 방법으로 윌콕슨 순위합(Wilcoxon rank sum) 또는 동일한 결과를 주는 맨-휘트니(Mann-Whitney) 방법이 있다[1]. 따라서 우리는 두 모집단의 평균을 비교할 때 모집단의 정규분포를 검토한 후, 모수적 방법을 사용할지 비모수적 방법을 사용할지를 먼저 선택하여야 한다. 특히 한 방향으로 치우친 자료에서, 만약 표본의 크기까지 작다면(일반적으로 각 군당 15미만이면 작다고 할 수 있음) 비모수적 방법을 사용하는 것이 좋다.
2) 상황 2
Dr. P는 세 가지 서로 다른 치료약 A, B, C의 효과를 치료 12주 후 HbA1c 농도(%)를 통해 평가하고자 한다. 수집한 자료는 각 군당 30명이다.
Dr. P는 두 모집단이 아니라 모집단의 개수가 3개이므로, 번거롭지만 두 집단씩 짝을 만들어서(치료약 A와 치료약 B, 치료약 A와 치료약 C, 그리고 치료약 B와 치료약 C와 같이) 독립된 두 집단의 t-검정을 3번 반복하는 것을 생각해 보았다. Dr. P의 임상적 가설은 무엇일까? 아마 연구를 통해 "세 치료약의 효과가 모두 같지는 않을 것이다"는 증거를 제시하고 싶을 것이다. 이러한 연구자의 가설(대립가설이라 함)에 반대되는 가설(귀무가설이라 함)은 무엇일까? "세 치료군의 효과가 모두 같다"일 것이다.
(1) 돌발 질문
독립된 두 집단의 t-검정을 반복적으로 3번 시행하자. 만약 3번의 t-검정에서 어느 하나라도 P<0.05 이면, 세 치료약의 효과는 모두 같다는 귀무가설을 기각한다면 어떤 문제가 있을까?
(2) Dr. S의 설명
이 질문의 핵심은 임상 의학연구에서 많이 범하는 오류 중 하나인 제 1종 오류의 증가와 관련된 매우 중요한 문제이다[1]. 만약 3개 집단의 모평균에 차이가 없다고 가정하자. 이 경우 각각의 t-검정에서 유의수준을 5%로 한 경우, 귀무가설을 기각할 확률은 0.05임을 알 수 있다. 따라서 해당하는 두 모집단의 평균이 같다는 귀무가설을 기각하지 못할 확률은 0.95이다. 만약 3번의 각 검정들이 독립이라고 가정하면, 3개의 t-검정 모두 두 모평균에 차이가 없다는 귀무가설을 기각하지 못할 확률은 (0.95)3 즉, 0.86 정도가 된다. 따라서 3개 집단의 모평균에 차이가 없다는 귀무가설이 사실일 때, 이러한 귀무가설을 기각할 확률(이를 제 1종의 오류라 함)은 0.14이고, 이 값이 일반적으로 사용하는 유의수준 0.05 보다 큰 값이다. 따라서 유의수준 0.05로 t-검정을 반복적으로 시행하여 통계적 결론을 도출할 때 실제로는 제 1종 오류가 0.05 보다 훨씬 크게 되는 잘못을 범하게 된다. 3개 이상의 모집단 평균을 비교할 때는 분산분석을 통해 이러한 문제를 해결하여야 한다. 위의 예제와 같이 HbA1c에 관련된 요인(이 경우는 3종류의 당뇨치료군)이 1개인 경우를 1요인 분산분석이라 한다. 물론 요인의 개수에 따라 2요인 분산분석, 3요인 분산분석 등이 있지만, 많은 의학연구에서는 2요인 분산분석 내에서 자료를 분석한다. 요인이 많은 경우는 다른 분석방법, 예를 들면 회귀분석과 같은 방법을 사용하는 것이 편리하다.
(3) Dr. P의 의문
첫째, 1요인 분산분석에 대응하는 비모수적 방법은 무엇일까? 둘째, 1요인 분산분석 결과, 귀무가설이 기각되었을 때 어떤 집단 간에 모 평균 차이가 있는지를 어떻게 알 수 있을까? 마지막으로 모집단의 분산이 모두 같다는 가정을 할 수 없는 경우에는 어떤 방법을 사용할 수 있을까?
(4) Dr. S의 설명
만일 비모수적 방법을 사용하여야 하는 경우에는 1요인 분산분석에 대응하는 비모수적 방법으로 크루스칼-왈리스 검정(Kruskal-Wallis test)이 있다. 그리고 1요인 분산분석에서 귀무가설이 기각된 경우, 다중비교(multiple comparison)를 통해 모집단들의 모평균 구조를 검정할 수가 있다[1].
3) 상황 3
Dr. P는 치료약 A의 효과를 치료 전에 비해 치료 12주 후 HbA1c 농도(%)의 변화를 통해 평가하고자 한다. 수집한 자료는 치료약 A를 투여 받은 30명의 치료 전과 치료 12주 후의 HbA1c이다.
Dr. P는 상황 1은 비교하고자 하는 집단이 독립된 두 집단이지만, 상황 2는 동일한 환자의 치료 전과 치료 12주 후 반복 측정된 형태임을 알 수 있다. 따라서 동일인의 치료 전 HbA1c와 치료 12주 HbA1c의 차이를 생각할 수 있다는 점이 독립된 두 집단의 t-검정자료와 다른 점임을 알 수 있다.
(1) Dr. S의 설명
만약 이러한 차이의 표본 평균이 0과 차이가 크다면, 치료 전, 후 모평균의 차이가 있다고 할 수 있을 것이며, 이런 원리로 만들어진 방법이 모수적 방법으로 paired t-검정, 비모수적 방법으로 윌콕슨 부호순위(Wilcoxon signed rank) 검정이 있다[1].
4) 상황 4
Dr. P는 치료약 A와 B의 효과 차이를 알기 위해, 투약 전(t0)에 Hb A1c 농도(%)를 측정하고 투약 후 16(t1)주에 HbA1c 농도(%)를 조사하였다.
Dr. P는 다음을 유추할 수가 있다. 만약, 관심 있는 가설이 치료 전에 비해 치료 16주 후의 변화가 두 군 간에 차이 있는 것이라면, 각 연구대상자의 치료 전, 후 HbA1c 농도(%)의 차이를 계산할 수가 있다. 따라서 이러한 차이의 평균이 두 치료군 간에 차이가 있는지를 독립된 두 집단의 t-검정, 경우에 따라서는 윌콕슨 순위합 검정을 통해 의사결정 할 수 있다.
그러나 치료 전 시점에서 두 치료군의 HbA1c 평균 차이가 있는지를 독립된 두 집단의 t-검정을 한 결과, 두 군 간에는 통계학적으로 유의한 차이가 있음을 발견하였다. 일반적으로 환자를 랜덤하게 두 치료군에 배정하는 임상시험인 경우에는 두 군 간에 특성의 차이가 거의 없게 되므로, 단순히 독립된 두 집단의 t-검정을 통해 가설을 검정할 수가 있다. 그렇지만, 많은 관찰연구에서는 두 치료군의 특성에 차이가 있을 수 있다.
(2) Dr. S의 설명
결론적으로 공분산분석(analysis of covariance) 또는 다중회귀분석(multiple regression)을 사용할 수가 있다. 공분산분석은 다중회귀분석과 동일한 결과를 주므로 다중회귀분석에 대해서만 간단히 알아보자[1].
먼저 변수들을 설명관계에 따라 독립변수와 종속변수로 구분한다. 다음으로 종속변수와 독립변수들의 함수적 관계를 설정하고, 이를 통해 독립변수로서 종속변수를 예측하거나 또는 종속변수와 통계학적으로 유의하게 관련된 독립변수들을 찾는 목적으로 회귀분석 방법이 많이 시행된다[4]. 이와 같은 다중회귀분석의 가장 큰 장점은 특정 독립변수와 종속변수의 관련성은 분석모형에 포함된 다른 독립변수들의 영향을 통제한 두 변수의 관련성 결과라는 것이다.
Dr. P는 다음을 유추할 수 있다. 상황 4에서 종속변수를 치료 전과 치료 16주 후의 HbA1c 차이(Y), 그리고 두 치료군을 구분하는 변수(X)와 치료 전 시점의 HbA1c (Z)를 독립변수로 하여 다음과 같은 다중 회귀분석모형을 구축할 수가 있다.
Y = α + β1X+ β2Z+ϵ
여기서, α, β1, β2 는 회귀계수(regression coefficient), ϵ은 정규분포를 따르는 오차항, X는 0이면 치료군 A, 1이면 치료군 B를 의미한다. 따라서 회귀계수 β1의 의미는 치료 전 HbA1c를 통제한 후, 치료군 A(기준집단)에 비해 치료군 B의 HbA1c 변화의 평균이 β1 만큼 더 높다이다. 그리고 β2는 치료 군을 통제한 후(즉, 동일 치료 군 내에서) 치료 전 HbA1c가 1% 증가하면 치료 전, 후 HbA1c의 평균 변화는 β2 만큼 증가한다는 것을 의미한다. 따라서 H0 : β1 = 0을 검정함으로써 치료 전 HbA1c를 통제한 후, 두 군 간에 HbA1c의 평균 변화에 통계학적으로 유의한 차이가 있는가를 검정할 수 있다.
(3) Dr. P의 의문
첫째, 다중 회귀분석에서 종속변수의 측정수준은 연속형, 범주형 모두 사용가능한가? 둘째, 독립변수의 측정수준은 연속형, 범주형 모두 사용가능한가? 셋째, 모형에 포함된 독립변수들 간에 관련성이 높은 경우 어떤 문제가 있는가?
(4) Dr. S의 설명
다중 회귀분석에서 종속변수는 정규분포를 따르는 연속형 변수이어야 한다. 만약 범주형 자료이면 뒤에서 다시 설명할 로지스틱 회귀분석, 생존형 자료이면 콕스회귀모형 등을 사용할 수 있다. 그렇지만 독립변수는 연속형과 범주형 모두 가능하다.
단, 만약 독립변수가 범주형 변수이면 반드시 가변수(dummy variable)로 바꾸어 회귀분석 모형에 포함하여야 한다. 만약 범주의 수가 k개이면 가변수는 (k-1)개를 만들어야 한다. 위의 모형에 포함된 두 치료군을 구분하는 변수 X는 범주형 변수이고 범주의 수가 2개이므로 가변수를 만들면 1개, 즉 X 변수 자체가 가변수가 된다. 만약 치료 군이 A, B, C 3군이면, 가변수는 2개를 만들어야 한다. 예를 들면, 치료군 A에 대한 치료군 B, 치료군 A에 대한 치료군 C를 비교하는 가변수 2개를 만들 수 있다[14].
또한, 다중공선성(multicollinearity)에 대한 확인이 필요하다. 다중공선성이란 모형에 포함된 독립변수들 간의 강한 선형적 관계를 의미하며, 만약 구축한 회귀모형에 다중공선성이 있으면 추정된 회귀계수의 표준오차는 상당히 커지게되므로 회귀계수의 유의성 검정은 그 의미를 잃는다. 다중공선성의 존재를 알아보는 방법에는 분산확대인자(variance inflation factor)를 확인하여 이 값이 10 이상이면 해당 독립변수는 다중공선성의 문제가 있다고 판단할 수 있다[14].
좋은 회귀모형을 만들기 위해서는 오차항의 등분산성과 독립성 등의 기본 가정을 검토하여야 한다. 또한 모형에 포함된 독립변수 수가 표본자료의 수에 비해 너무 많지는 않는지 그리고 독립변수와 종속변수의 함수적 관계는 적합한지 등을 검토하여야 한다.
5) 상황 5
Dr. P는 치료약 A (30명)와 B (30명)의 효과 차이를 알기 위해, 투약 전(t0)에 HbA1c 농도(%)를 측정하고 투약 후 4주(t1), 8주(t2), 12주(t3), 16(t4)주에 각각 HbA1c 농도(%)를 조사하였다.
Dr. P는 다음을 구체적으로 알아보고자 한다. 두 군 간에 HbA1c 변화에 차이가 있는가? 또한 시간에 따른 변화가 있는가? 그리고 시간에 따른 변화가 두 치료군 간에 차이(교호작용)가 있는가?
Dr. P는 상황 4는 동일 환자에서 치료 전, 후 차이를 의미하는 종속변수가 1개이지만, 상황 5는 4개, 즉 Y1 (t1과 t0의 HbA1c 차이), Y2 (t2와 t0의 HbA1c 차이), Y3 (t3와 t0의 HbA1c 차이), 그리고 Y4 (t4와 t0의 HbA1c 차이)이다. 그런데 이들 4개의 종속변수들 간에는 상관성이 존재하는 독립된 자료가 아님을 알 수 있다.
(1) Dr. S의 설명
먼저 논의를 간단히 하기 위해, 시간에 따른 변화가 두 치료군 간에 차이는 없다고 하자. 즉 교호작용은 없다고 가정하자.
일단 다음과 같이 자료구조를 바꾸면, 자료의 형태로는 다중 회귀분석을 할 수 있을 것 같다. 먼저, 각 환자마다 수평으로 입력된 4개의 종속변수 Y1,Y2,Y3,Y4 값을 수직으로 변환하자. 변환된 자료구조는, 치료 전과 특정 시점에 대한 HbA1c 차이(Y), 두 치료군을 구분하는 변수(X), 치료 전 시점의 HbA1c (Z), 그리고 시점에 대한 시간변수(T)로 구성할 수 있다. 따라서 전체 240건(60명×4)의 관찰치가 수직형태로 위의 변수들로 구성할 수 있다. 수직으로 변환된 구조에서 다음과 같은 회귀모형을 일단 생각해보자.
Y = α + β1X+ β2Z+ β3T+ϵ
다중회귀분석에서 오차항 ϵ은 독립성을 가정하였지만, 위의 자료에서는 동일한 환자가 4개의 값을 가지므로 이들 간에는 독립성을 가정할 수가 없고 서로 상관성이 있을 것이다. 따라서 동일한 환자에 해당하는 자료 간에 적절한 형태의 상관성(또는 분산-공분산) 구조를 가정하고 분석하면 이러한 문제를 해결할 수 있지 않을까? 이것이 일종의 혼합모형(mixed model)을 이용한 분석방법 중 하나이다[5]. 보조적으로 위의 모형에서 시점독립변수 T는 연속형이 아닌 범주형으로 간주하여, 가변수로 처리할 수도 있다.
따라서 상황 5는 선형혼합모형(linear mixed model)을 이용하여 분석할 수 있다. 우리가 많이 사용하는 통계 프로그램에서는 설명한 것과 같이 자료 구조를 쉽게 바꿀 수가 있고 그리고 다양한 분산-공분산 행렬의 구조를 가정할 수가 있다.
2. 치료약의 효과를 혈당 조절 여부로 측정한 경우
1) 상황 6
Dr. P는 치료의 효과를 치료 12주 후 혈당 조절 여부로 평가하고자 한다. 수집한 자료는 치료제 A를 투여 받은 50명과 치료제 B를 투여 받은 50명이다.
Dr. P는 변수 Y의 자료 입력을 혈당이 조절된 사람을 '1' (HbA1c <6.5%), 조절되지 않은 사람을 '2' (HbA1c ≥ 6.5%)로 입력하였다. 또한 변수 X를 A 치료군은 '1', B 치료군은 '2'로 입력하였다. 기초 자료를 분석한 결과 치료약 A를 투여한 군에는 50명 중 30명(60%), B를 투여한 군에는 50명 중 40명(80%)의 혈당이 조절되었다. 자료의 형태로 보면 모집단의 평균비교가 아니라 두 모집단의 혈당 조절 확률(백분율)에 차이가 있는가를 검정하면 된다.
(1) Dr. S의 설명
범주형으로 측정된 변수들 사이의 관련성을 분석하는 방법으로 카이제곱 검정이 있다[16]. 위의 자료는 각각 2개의 범주를 갖는 치료군 변수(X)와 혈당조절 여부를 나타내는 변수(Y)를 서로 교차하여 분할표를 구성할 수 있다. 카이제곱 검정의 기본 원리는 4개의 칸에서 관측된 실제 관측빈도수와 귀무가설(위의 예제에서는 두 치료군의 혈당 조절률이 같다)이 사실이라는 가정 하에서 계산된 기대빈도수의 차이를 이용하여 분석하는 방법이다. 예를 들어 분할표의 (1행, 1열), 즉, 치료군 A에 속한 환자 중에서 혈당이 조절된 관측빈도수는 30명이다. 두 치료군의 조절률에 차이가 없다는 가정에서, 전체 혈당 조절률은 0.7(70/100)이고, 따라서 치료군 A에 속한 50명에서 혈당이 조절되는 기대빈도수는 35명(0.7×50)으로 추정할 수 있고, 나머지 분할표의 칸에서도 기대 빈도수를 동일한 방법으로 계산할 수 있다.
(2) Dr. P의 의문
첫째, 기대빈도수가 작은 경우에도 카이제곱 검정을 사용할 수 있는가? 둘째, 독립된 두 집단의 t-검정과 짝을 이룬 paired t-검정의 관계와 같이 두 독립된 집단의 확률을 비교할 때 카이제곱 검정을 사용한다면 독립이 아니고 짝을 이룬 경우에는 어떤 방법을 사용할 수 있는가? 마지막으로 혈당조절에 영향을 미치는 중요한 변수가 있는 경우, 이 변수의 영향을 통제하면서 두 치료군의 혈당 조절률에 차이가 있는지를 알아보는 방법은 무엇인가?
(3) Dr. S의 설명
만약 기대빈도수가 작은(일반적으로 5 미만) 칸이 있다면 피셔의 정확도(Fisher's exact test) 검정을 하는 것이 좋다[16]. 그리고 같은 환자 내에서 일정기간 동안 A 치료약으로 치료한 후 혈당 조절 여부를 측정하고, 그리고 휴약기를 가진 다음 A 치료약을 투여하기 전과 같은 상황에서 다시 B 치료약으로 치료한 후 혈당 조절 여부를 측정한 경우에는 동일인 내에서 얻어진 자료이므로 카이제곱 검정 대신 멕네머(McNemar) 검정을 통하여 두 치료군의 혈당 조절 확률의 차이를 검정하여야 한다[6].
마지막으로, 다른 변수의 영향을 통제하기 위해서는 회귀분석 기법을 사용하여야 한다. 다중회귀분석은 종속변수가 정규분포를 따르는 경우에 사용하지만, 만약 위의 상황과 같이 종속변수가 범주형인 경우에는 로지스틱(logistic regression) 회귀분석을 사용할 수 있다. 일반적으로 종속변수의 범주의 수가 2개인 경우, 이분형(binary) 로지스틱 회귀모형, 범주의 수가 3개 이상인 경우에는 다항 로짓 모형(multinomial logit model)이나 누적로짓 모형(cumulative logit model)을 사용할 수 있다[14].
예를 들어 종속변수를 치료 후 반응이라 하고, 1=완전반응, 2=부분 반응, 3=비반응으로 측정하였다고 하자. 일단 범주의 수가 3개이므로, 다항 로짓 모형이나 누적 로짓 모형을 적용할 수 있다. 만약 위의 예와 같이 범주의 특성에 순서(order)가 있는 경우(즉, 값이 커질수록 반응이 좋지 않다)에는 두 모형 모두 사용하는 것이 가능하지만, 순서가 없다면 다항 로짓 모형을 사용하여야 한다. 하지만 범주 간에 순서가 있다 할지라도 비례오즈(proportional odds)라는 가정을 만족하지 못하면 다항 로짓을 사용하여야 한다. 비례오즈 가정에 대한 검토는 스코어 통계량을 이용하여 검정할 수 있다.
앞서 말한 다중회귀분석과 같이 독립변수가 범주형이면 가변수 처리를 하여야 하고, 독립변수들 간에 높은 선형적 관련성이 있으면 다중공선성 문제가 발생할 수 있으므로 가급적 독립변수의 수는 적으면서 모형의 설명력이 높은 모형을 만드는 것이 중요하다[4].
3. 치료약의 효과를 심혈관계 질환 사망위험으로 비교하는 경우
1) 상황 7
Dr. P는 치료의 효과를 치료시작 후 5년간 환자들을 추적하면서 심혈관계 질환으로 인한 사망의 위험을 비교하고자한다. 수집한 자료는 치료제 A를 투여 받은 1,000명과 치료제 B를 투여 받은 1,000명이다.
Dr. P는 상황 6과 비교하여 다음과 같은 자료의 차이점을 발견할 수 있다. 앞의 자료는 환자들의 12주 후 혈당조절 여부만을 조사하였고, 모든 환자들은 동일하게 12주를 관찰하였다. 하지만 상황 7은 심혈관계 질환으로 인한 사망이 발생할 때까지의 시간을 추적 관찰하며, 이런 경우 불완전한 자료가 발생할 수 있다.
(1) 돌발 질문
어떤 환자가 치료 시작 후 3년 동안 심혈관계 질환으로 사망하지 않았으나, 그 이후는 추적관찰 할 수 없어 사망여부를 판단할 수 없었다. 이런 경우 카이제곱 분석방법은 할 수가 없으므로 이런 대상자들을 분석에서 제외하면 어떨까?
(2) Dr. S의 설명
다음과 같은 이유로 이런 환자들을 제외하는 것은 문제가 있다. 만약 첫 번째 환자는 1년 시점에서 관심 있는 사건이 발생하였고, 두 번째 환자는 2년 시점까지는 사건이 없었으나 그 이후는 추적할 수가 없었고, 세 번째 환자는 3년 시점에서 관심 있는 사건이 발생하였다면, 두 번째 환자는 사건발생 시간에 대한 자료가 불완전하지만, 정보가 전혀 없는 것은 아니다. 첫 번째 환자보다는 사건발생 시간이 길고, 2년까지는 사건이 발생하지 않았으며, 2년이 지난 시점부터는 정보가 불완전하므로 세 번째 환자와는 누가 사건발생 시간이 긴지를 비교할 수가 없다. 어떤 관심 있는 사건이 발생할 때까지 시간을 생존시간(survival time)이라 정의한다. 연구 대상들의 생존시간을 관측할 때, 위의 두 번째 환자와 같이 더 이상 추적을 할 수 없거나, 또는 5년이 경과한 연구종료 시점에서도 사건이 발생하지 않은 대상자가 있다. 이와 같이 어떤 관심 있는 사건이 발생할 때까지를 추적 관찰하는 경우, 여러 가지 이유로 사건 발생여부에 대해 불확실한 자료가 발생할 수 있으며, 이를 중도절단(censored)된 자료라 한다. 생존분석은 중도 절단된 자료의 정보를 최대한 활용하여 분석하는 방법이다. 시간이 경과함에 따라 사건이 계속 발생하므로, 시간에 대한 생존함수 S(t)를 t 시간까지 사건이 발생하지 않을 확률로 정의하자.
따라서 상황 7은 두 치료군의 생존함수를 각각 그려보고, 이를 비교하는 통계적 방법을 적용할 수가 있다. 임상연구에서 생존함수를 추정할 때 가장 많이 사용하는 방법으로 Kaplan-Meier 방법이 있고, 여러 치료군들의 생존함수를 비교할 때는 로그-순위 검정 또는 Breslow 검정을 사용할 수 있다[17].
이들 검정법의 절차는 먼저 모든 시점에서 위험집단(risk set)을 구성한다. t-시점에서의 위험집단은 t-시점까지 사건이 발생하지 않았거나 중도절단 되지 않은, 앞으로 사건이 발생할 가능성이 있는 대상자 집합이다. 다음으로 사건이 발생한 각 시점마다 그 시점에서 위험집단에 속한 대상자 중 어떤 치료군에서 사건이 발생하였는지 분할표를 구성한다. 이와 같은 방법으로 분할표를 구성하면 중도절단된 자료의 정보가 충분히 반영됨을 알 수 있다. 마지막으로 각 시점에서의 분할표를, 로그-순위 검정은 동일한 가중치, Breslow 방법은 초기 시점에 큰 가중치를 두고 병합하는 방법이다[7].
생존형 자료에서 회귀분석 방법으로는 콕스 회귀모형을 많이 사용한다. 콕스 회귀모형은 비례위험(proportional hazard)을 가정하고 있다. 즉 두 군의 위험함수 비가 시간에 따라 변하지 않는다는 비례위험 가정을 검토한 후 사용하여야 한다. 비례위험 가정은 두 군의 log(-log(S(t)) 함수가 시간에 따라 평행하다는 것을 보임으로써 검토할 수 있다[7].
결론
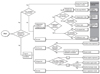
모든 연구자는 본인의 연구 가설이 지지되기를 희망할 것이며, 잘 계획된 연구설계를 통해 얻어진 결과는 좀 더 진실된 관계를 제시할 것이다. 임상연구에서 가장 중요한 것은 연구가설에 적합한 좋은 연구설계를 하는 것이다. 본 논문은 연구설계에 초점을 두기 보다는 연구설계에 따라 자료를 수집한 후 어떤 통계학적 검정방법을 사용하는 것이 좋을지에 초점을 두어 설명하였다. 즉, 자료의 특성에 따른 여러 가지 상황을 설정하고, 각 상황별 어떤 통계학적 검정들을 사용하는 것이 좋을지를 비교, 설명하였다. 본 논문에서 언급한 여러 가지 통계적 방법들을 정리한 Figure 1의 순서도가 이 글을 읽는 임상, 의학연구자 분들에게 조금이라도 도움이 되기를 희망하며 두 연구자의 대화를 마치고자 한다.
Peer Reviewers' Commentary
본 논문은 의학연구 특히, 임상연구에서 연구결과 도출과정에 필수적인 통계학적 의사결정 방법을 다루었다. 필자의 충만한 이론적 지식을 바탕으로 풍부한 임상연구 통계상담 경험에서 비롯된 분석방법의 선정이 돋보이며 다소 거리감을 느낄 의학자들에게 친근감 있게 대화체로 기술 한 점이 높이 평가되고 결론의 도표는 통계분석법 선택에 많은 도움이 될 것으로 보인다. 대한의사협회지가 국제적 공신력을 높혀 가는 단계에서 통계분석법을 간단명료하게 다룬 것은 시의 적절하다고 판단되며 학회지에 연구결과를 투고하고자 하는 연구자들에게 많은 도움이 될 것으로 기대 된다.
[정리: 편집위원회]
XML Download