PDF
ePub
Citation
Print
Abstract
Trotter and Gleser's (1958) Asian equations have most frequently been used for stature estimation of Korean skeletal remains. However, limitations or caveats in using those equations have rarely been argued. This study reviews five issues frequently overlooked in applying the equations and interpreting the outcomes.
First, Trotter and Gleser (1958) multiply the standard errors by 2 to obtain the 95% prediction interval (PI). However, there is discrepancy between their calculation and actual PIs, and thus correct method for PI calculation is recommended. Secondly, given the uncertainty about the tibia length measurement, there is a possibility that the tibia-related equations yield biased estimates. Thirdly, since a mathematical error was incorporated in the development process of the combined equations, caution should be taken. Fourthly, extrapolation may cause additional unexpected error in applying regression equations. Therefore, it is necessary to check if a target sample falls within the reference sample range prior to using the equations. Lastly, applying Trotter and Gleser's (1958) equations to female samples should be avoided because they produce highly biased estimates.
The issues discussed in this study will contribute to reducing potential errors associated with application of these equations, and eventually enhancing accuracy of the final stature estimates. If errors are anticipated but unavoidable, discussions about the potential errors should be made to minimize misunderstanding about the outcomes.
References
1. Cha MS, Cho YJ. Trend in the Korean stature, 1540–1885. Presented at the Asian Historical Economic Congress, Tokyo, Japan;. 2012.
2. Malina RM, Reyes MEP, Little BB. Secular Change in Heights of Indigenous Adults From a Zapotec-Speaking Community in Oaxaca, Southern Mexico. Am J Phys Anthropol. 2010; 141:463–75.
3. Ulijaszek S, Komlos J. From a history of anthropometry to anthrometric history. In: Mascie-Taylor CGN, Yasukouchi A, Ulijaszek S (eds.). Human variation: from the laboratory to the field. CRC press;2010. ;p.p. 183–98.
4. Cohen MN, Crane-Kramer GMM. Ancient health: skeletal indicators of agricultural and economic intensification. Gainesville: University Press of Florida;2007.
5. Steckel RH, Rose JC. The backbone of history: health and nutrition in the Western Hemisphere. Cambridge:. New York: Cambridge University Press;2002.
6. Bogin B. Patterns of human growth (2nd ed.). Cambridge, U.K:. New York: Cambridge University Press;1999.
7. Ruff C. Morphological adaptation to climate in modern and fossil hominids. Yearb Phys Anthropol. 1994; 37:65–107.
8. Frayer DW. Biological and cultural change in the European Late Pleistocene and Early Holocene. In: Smith FH, Spencer F (eds.). The origins of modern humans: a world survey of the fossil evidence. New York: Wiley-Liss;1984. ;p.p. 21150.
9. Moore MK, Ross AH. Stature Estimation. In: DiGAngi EA, Moore MK (eds.). Research Methods in Human Skeletal Biology. Academic Press;2013. ;p.p. 151–79.
10. Wilson RJ, Herrmann NP, Jantz LM. Evaluation of Stature Estimation from the Database for Forensic Anthropology. J Forensic Sci. 2010; 55:684–9.
11. Lundy JK. A report on the use of Fully's anatomical method to estimate stature in military skeletal remains. J Forensic Sci. 1988; 33:534–9.
12. Fully G. Une nouvelle méthode de détermination de la taille (New method of determination of the height). Ann Med Leg Criminol Police Sci Toxicol. 1956; 36:266–73.
13. Trotter M, Gleser GC. Estimation of stature from long bones of American Whites and Negroes. Am J Phys Anthropol. 1952; 10:463–514.
14. Ruff CB, Holt BM, Niskanen M, Sladek V, Berner M, Garofalo E, et al. Stature and body mass estimation from skeletal remains in the European Holocene. Am J Phys Anthropol. 2012; 148:601–17.
15. Raxter MH, Auerbach BM, Ruff CB. Revision of the fully technique for estimating statures. Am J Phys Anthropol. 2006; 130:374–84.
16. Dwight T. Methods of estimating the height from parts of the skeleton: Trow Directory;. 1894.
17. Raxter MH, Ruff CB, Azab A, Erfan M, Soliman M, El-Sawaf A. Stature estimation in ancient Egyptians: A new technique based on anatomical reconstruction of stature. Am J Phys Anthropol. 2008; 136:147–55.
18. Pearson K. Mathematical contribution to the theory of evolution. V. On the reconstruction of the stature of prehistoric races. Philos T R Soc Lond. 1899; 192:169–244.
19. Trotter M, Gleser GC. A re-evaluation of estimation of stature based on measurements of stature taken during life and of long bones after death. Am J Phys Anthropol. 1958; 16:79–123.
20. Jeong Y. Secular change in stature and body mass in Korea over the last two millennia. Doctoral Dissertation. University of Tennessee, Knoxville;. 2014.
21. Duyar I, Pelin C. Estimation body height from ulna length: need of a population-specific formula. Eurasian J Anthropol. 2010; 1:11–7.
22. Giles E, Klepinger LL. Confidence intervals for estimates based on linear regression in forensic anthropology. J Forensic Sci. 1988; 33:1218–22.
23. Jantz RL, Hunt DR, Meadows L. Maximum Length of the Tibia – How Did Trotter Measure It. Am J Phys Anthropol. 1994; 93:525–8.
24. Jantz RL, Hunt DR, Meadows L. The Measure and Mismeasure of the Tibia – Implications for Stature Estimation. J Forensic Sci. 1995; 40:758–61.
25. Trotter M. Estimation of stature from intact long limb bones. In: Stewart TD (ed.). Personal identification in mass disasters. National Museum of Natural History, Smithsonian Institution. Washington DC;1970. ;p.p. 71–83.
26. Palloni A, Guend A. Stature prediction equations for elderly Hispanics in Latin American countries by sex and ethnic background. J Gerontol A-Biol. 2005; 60:804–10.
27. Maijanen H, Niskanen M. New Regression Equations for Stature Estimation for Medieval Scandinavians. Int J Os-teoarchaeol. 2010; 20:472–80.
28. Bermudez OI, Becker EK, Tucker KL. Development of sex-specific equations for estimating stature of frail elderly Hispanics living in the northeastern United States. Am J Clin Nutr. 1999; 69:992–8.
29. Chumlea WC, Guo SS, Wholihan K, Cockram D, Kuczmarski RJ, Johnson CL. Stature prediction equations for elderly non-Hispanic white, non-Hispanic black, and Mexican-American persons developed from NHANES III data. J Am Diet Assoc. 1998; 98:137–42.
30. Genovés S. Proportionality of Long Bones and Their Relation to Stature among Mesoamericans. Am J Phys Anthropol. 1967; 26:67–77.
31. Ousley S. Should We Estimate Biological or Forensic Stature. J Forensic Sci. 1995; 40:768–73.
32. Zar JH. Biostatical analysis (5th edition). Prentice Hall, NJ;. 2010.
33. Field A. Discovering statistics using IBM SPSS statistics (4th edition). London: SAGE Publications Ltd.;2013.
34. Konigsberg LW, Hens SM, Jantz LM, Jungers WL. Stature estimation and calibration: Bayesian and maximum likelihood perspectives in physical anthropology. Yearb Phys Anthropol. 1998; 41:65–92.
35. Pak S. An estimation of adult males'average stature from the skeletal remains of Joseon period. Korean J Phys Anthropol. 2011; 24:185–93.
36. Jeong Y, Jantz LM, Woo EJ, Jang Y. Quantifying bias in applying the Asian equations of Trotter and Gleser (1958) to Korean samples. presented at the 67th annual meeting of American Academy of Forensic Sciences, Orlando, FL;. 2015.
37. Jeong Y, Jantz LM. Developing Korean-specific equations of stature estimation. Forensic Sci Int. 2016; 260:105.e111.
38. Lee JH, Kim YS, Lee UY, Park DK, Jeong YK, Lee NS, et al. Stature estimation from partial measurements and maximum length of lower limb bones in Koreans. Australian J Forensic Sci. 2014; 46:330–8.
39. Lee JH, Jeong YK, Lee NS, Han SY, Han SH. Stature estimation from partial measurements and maximum length of upper limb bones in Koreans. Int J Research Granthaa-layah. 2015; 3:100–7.
Fig. 1.
(A) tibia maximum length by Trotter and Gleser's [13,19] definition; (B) actual length measured by Trotter and Gleser [13].
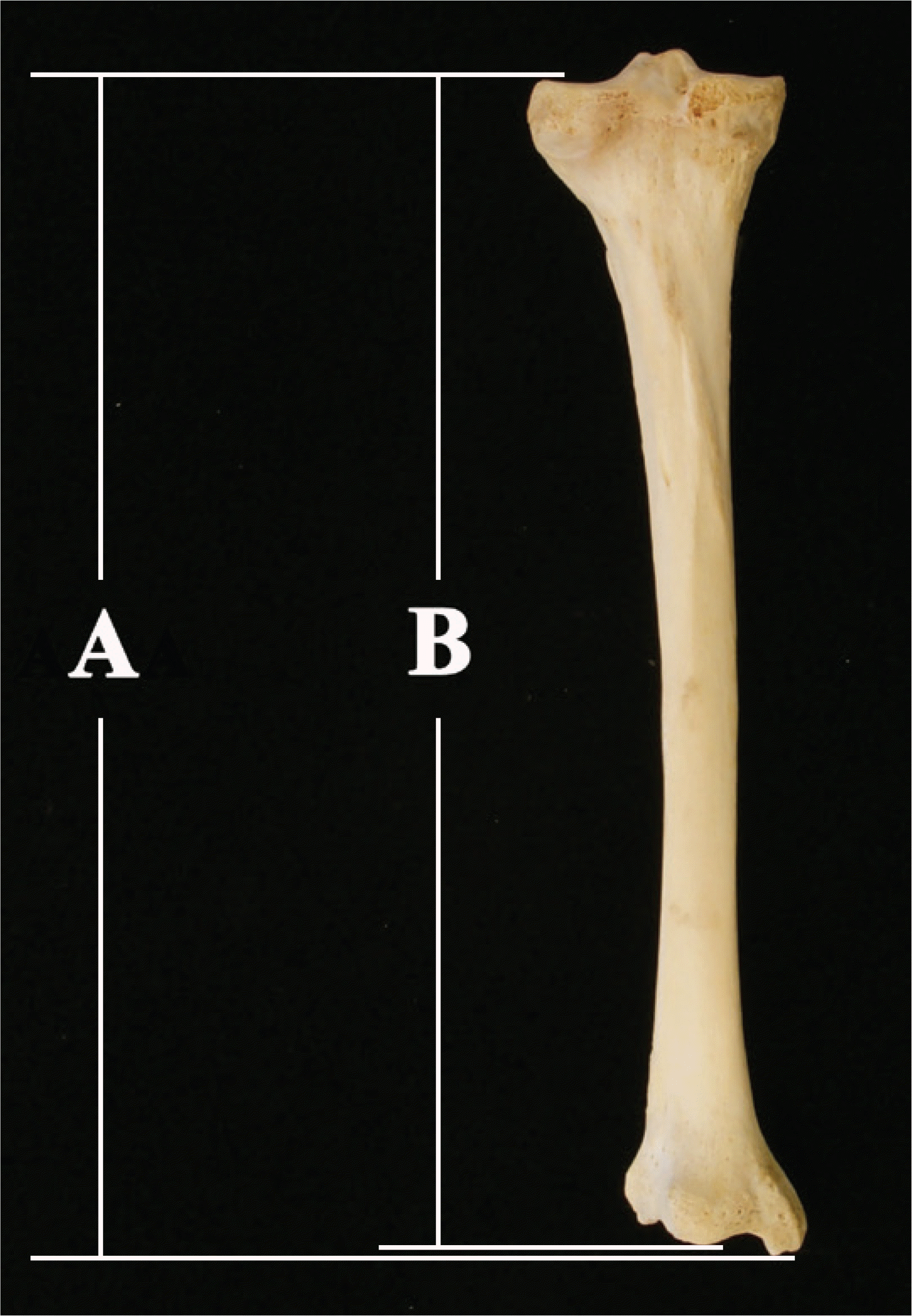
Fig. 2.
Exemplified diagram showing the relationship between the regression line where statures are regressed on actual average bone lengths (Line 1) and the regression line representing Trotter and Gleser's [19] combined equation (Line 2).
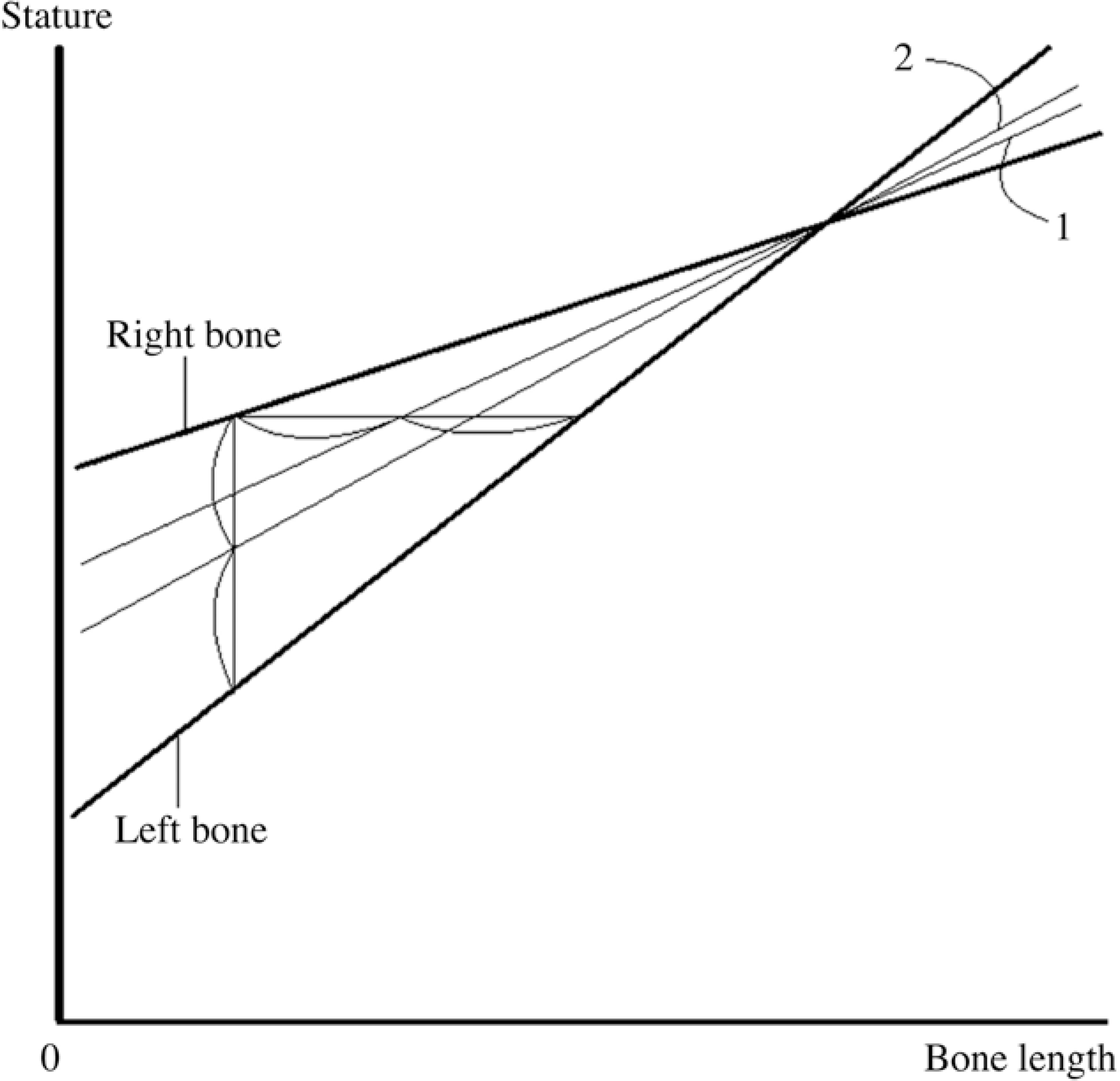
Fig. 3.
Exemplified diagram showing two variables of a curvilinear relationship. Note that, despite their true relationship, the graph in a boxed range is nearly linear.
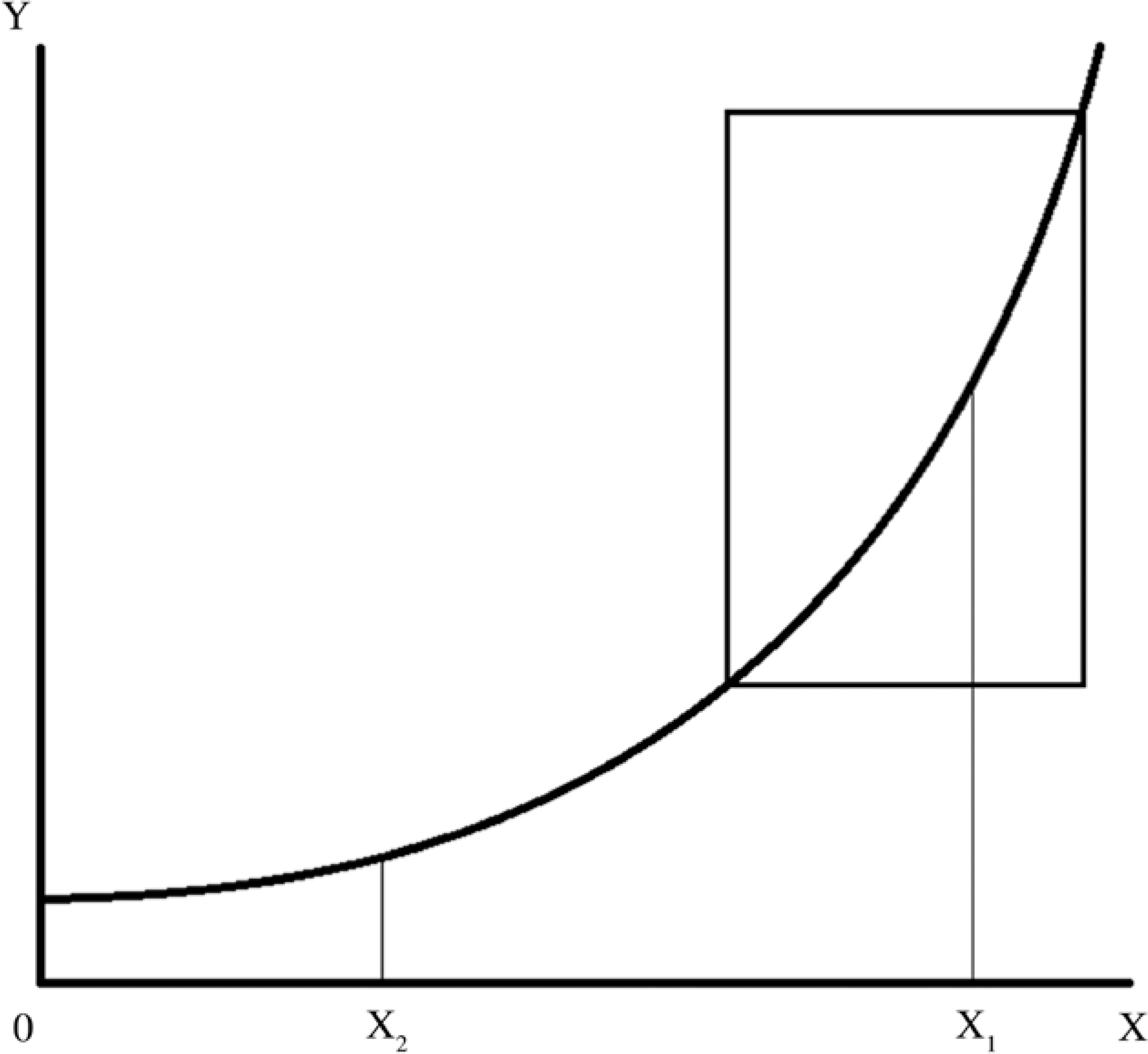
Fig. A-1.
Exemplified diagram showing the relationship between two individuals. Individual 1 with a stature Y1 possesses left and right bones of X1L and X2L; Individual 2 with a stature Y2 possesses left and right bones of X2L and X2R.
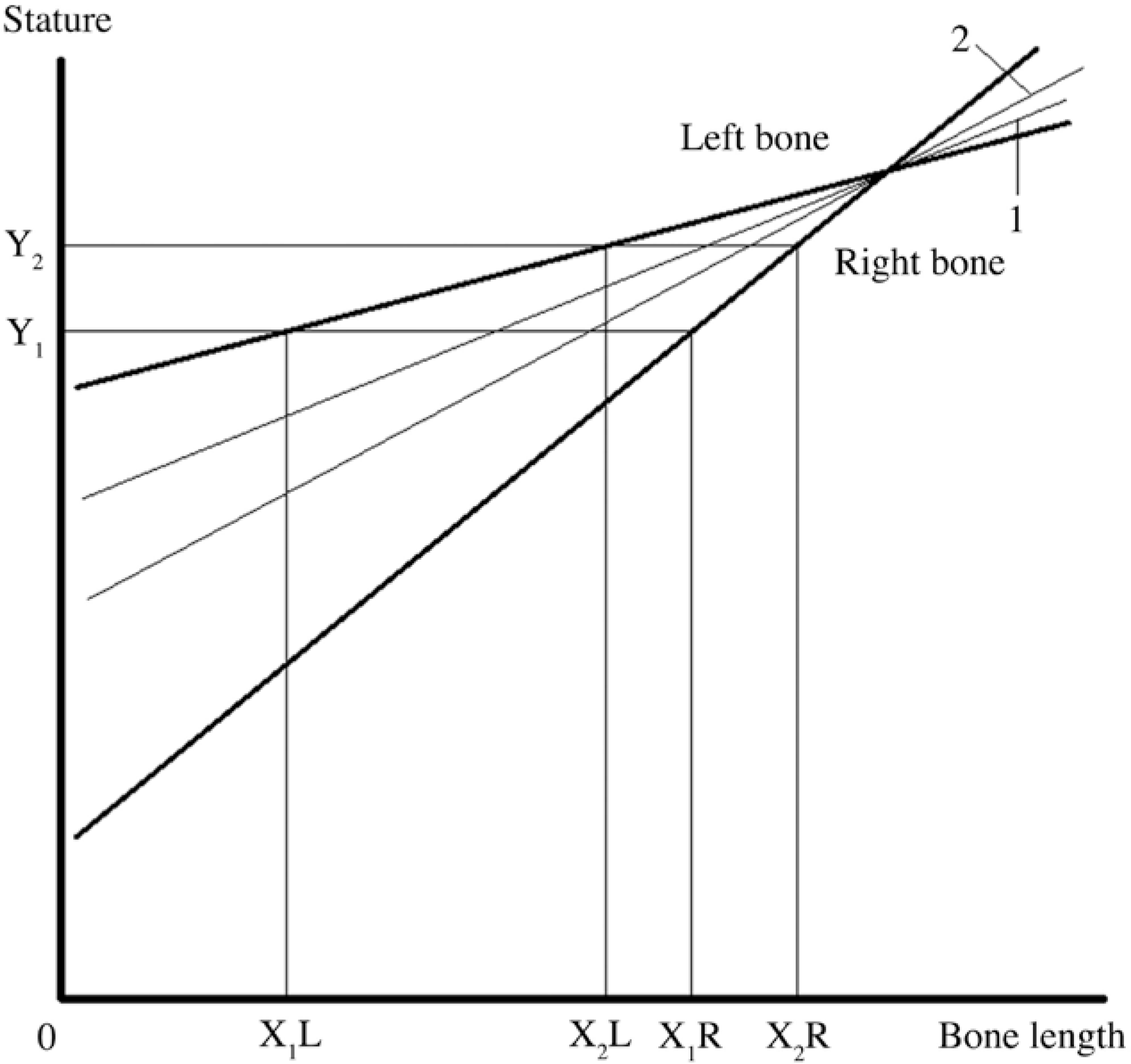
Table 1.
Bone lengths of the Asian samples in Trotter and Gleser [19].
XML Download