Analysis of stress distribution of tooth restored with metal-ceramic crown covering abfraction lesion according to its finish line location under occlusal load

Jee-Hwan Kim; Chol-Wook Yoon; Taehyeon Kim; Han-Sung Kim; Dae-Gon Woo; Keun-Woo Lee; June-Sung Shim

doi:10.4047/jkap.2014.52.4.305

Journal List > J Korean Acad Prosthodont > v.52(4) > 1034797

Go to TopGo to Top Go to BottomGo to Bottom

TOOLS

Kim, Yoon, Kim, Kim, Woo, Lee, and Shim: Analysis of stress distribution of tooth restored with metal-ceramic crown covering abfraction lesion according to its finish line location under occlusal load

Original Article

J Korean Acad Prosthodont 2014;52(4):305-311.

Published online: 9 February 2014

DOI: https://doi.org/10.4047/jkap.2014.52.4.305

Analysis of stress distribution of tooth restored with metal-ceramic crown covering abfraction lesion according to its finish line location under occlusal load

Jee-Hwan Kim^1,^a, Chol-Wook Yoon^1,^a, Taehyeon Kim¹, Han-Sung Kim², Dae-Gon Woo³, Keun-Woo Lee¹, June-Sung Shim^1,^∗

¹Department of Prosthodontics, School of Dentistry, Yonsei University, Seoul, Republic of Korea

²Department of Medical Device Evaluation, Cardiovascular Devices Division, Yonsei University, Seoul, Republic of Korea

³Korea Food and Drug Administration, Seoul, Republic of Korea

^∗Corresponding Author: June-Sung Shim Department of Prosthodontics, School of Dentistry, Yonsei University 50 Yonsei-ro, Seodaemun-gu, Seoul, 120-752, Republic of Korea +82 2 2228 8713: e-mail, jfshim@yuhs.ac

^∗ This study was supported by a faculty research grant of Yonsei University College of Dentistry for 2014 (6-2014-0092).

^a These authors contributed equally to this work.

Received 20 August 201425 September 2014 Accepted 26 September 2014

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Purpose

When the full veneer crown was treated in the tooth with abfraction lesion due to various causes, the prognosis of it may be compromised according to the location of the finish line, but there is few study about the location of its buccal finish line. The purpose of this study was to investigate the effect of location of the finish line of the full veneer crown on stress distribution of the tooth with abfraction lesion.

Materials and methods

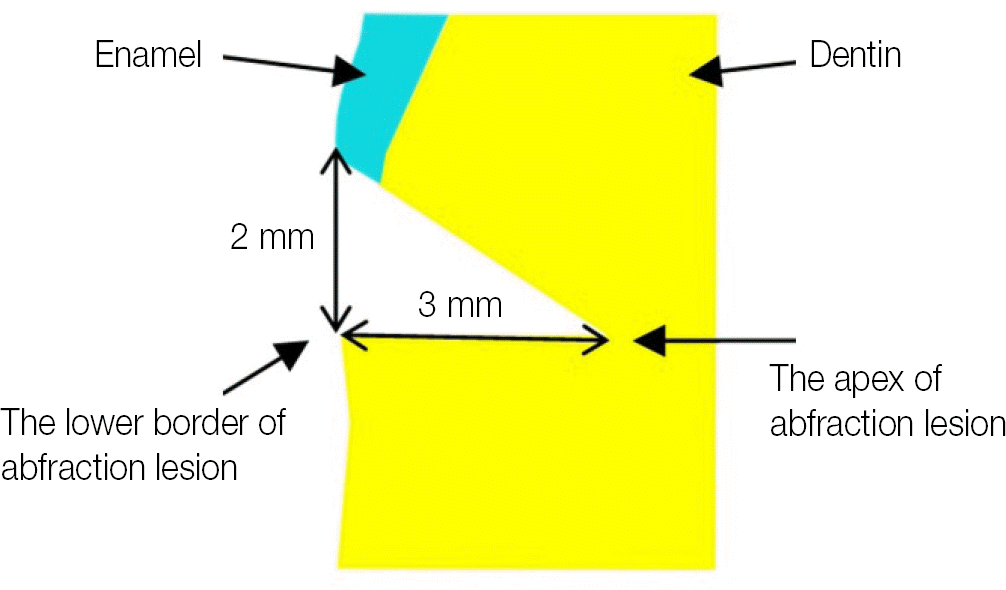
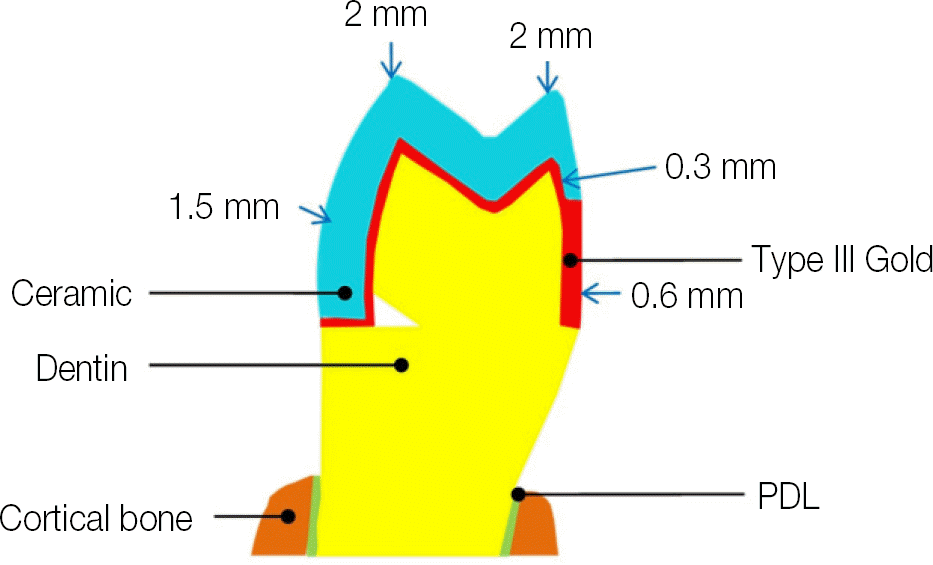
The two dimensional finite element model was developed to express tooth, surrounding tissue and full veneer crown. The stress distribution under eccentric 144 N occlusal load was analyzed using finite element analysis. The location of finish line was set just at the lower border of the lesion (Group 0), 1 mm (Group 1) and 2 mm (Group 2) below the lower border of the lesion.

Results

In the Group 0, von Mises stress was concentrated at the finish line and the apex of the lesion. Also, the stress at the bucal finish line propagated to the lingual side. In the Group 1 and Group 2, stress distribution was similar each other. Stress was concentrated at the apex of lesion, but the stress at the buccal finish line did not propagate to the lingual side. That implied decrease of the possibility of horizontal crown fracture.

Conclusion

Full veneer crown alleviated the stress concentrated at the apex of the abfraction lesion, when the finish line of full veneer crown was set below the lower border of abfraction lesion.

Keywords: Abfraction, Metal-ceramic crown, Finish line, Stress distribution, Finite element analysis

REFERENCES

1. Grippo JO. Abfractions: a new classification of hard tissue lesions of teeth. J Esthet Dent. 1991; 3:14–9.

2. Lee WC, Eakle WS. Possible role of tensile stress in the etiology of cervical erosive lesions of teeth. J Prosthet Dent. 1984; 52:374–80.

3. Rees JS. The effect of variation in occlusal loading on the development of abfraction lesions: a finite element study. J Oral Rehabil. 2002; 29:188–93.

4. Francisconi LF, Graeff MS, Martins Lde M, Franco EB, Mondelli RF, Francisconi PA, Pereira JC. The effects of occlusal loading on the margins of cervical restorations. J Am Dent Assoc. 2009; 140:1275–82.

5. Ichim I, Schmidlin PR, Kieser JA, Swain MV. Mechanical evaluation of cervical glass-ionomer restorations: 3D finite element study. J Dent. 2007; 35:28–35.

6. Grippo JO. Noncarious cervical lesions: the decision to ignore or restore. J Esthet Dent. 1992; 4:55–64.

7. Rosenstiel SF, Land MF, Fujimoto J. Contemporary fixed prosthodontics. 3rd ed.St. Louis: Mosby;2001. xi. p. 868.

8. Rubin C, Krishnamurthy N, Capilouto E, Yi H. Stress analysis of the human tooth using a three-dimensional finite element model. J Dent Res. 1983; 62:82–6.

9. Rees JS, Jacobsen PH. Modelling the effects of enamel anisotropy with the finite element method. J Oral Rehabil. 1995; 22:451–4.

10. Yaman SD, Alaçam T, Yaman Y. Analysis of stress distribution in a maxillary central incisor subjected to various post and core applications. J Endod. 1998; 24:107–11.

11. Versluis A, Douglas WH, Cross M, Sakaguchi RL. Does an in-cremental filling technique reduce polymerization shrinkage stresses? J Dent Res. 1996; 75:871–8.

12. Palamara D, Palamara JE, Tyas MJ, Messer HH. Strain patterns in cervical enamel of teeth subjected to occlusal loading. Dent Mater. 2000; 16:412–9.

13. Sorensen JA, Engelman MJ. Ferrule design and fracture resistance of endodontically treated teeth. J Prosthet Dent. 1990; 63:529–36.

14. Rees JS, Jacobsen PH. Elastic modulus of the periodontal liga-ment. Biomaterials. 1997; 18:995–9.

15. Vincent JFV. Structural biomaterials. Rev. ed.Princeton, NJ: Princeton University Press;1990. xii:p. 244.

16. Lewinstein I, Banks-Sills L, Eliasi R. Finite element analysis of a new system (IL) for supporting an implant-retained cantilever prosthesis. Int J Oral Maxillofac Implants. 1995; 10:355–66.

Fig. 1.

2-dimensional normal tooth geometry.

Fig. 2.

Abfraction finite element model.

Fig. 3.

Dimension of wedge-shaped defect.

Fig. 4.

Minimum recommended dimensions for a metal-ceramic restoration.

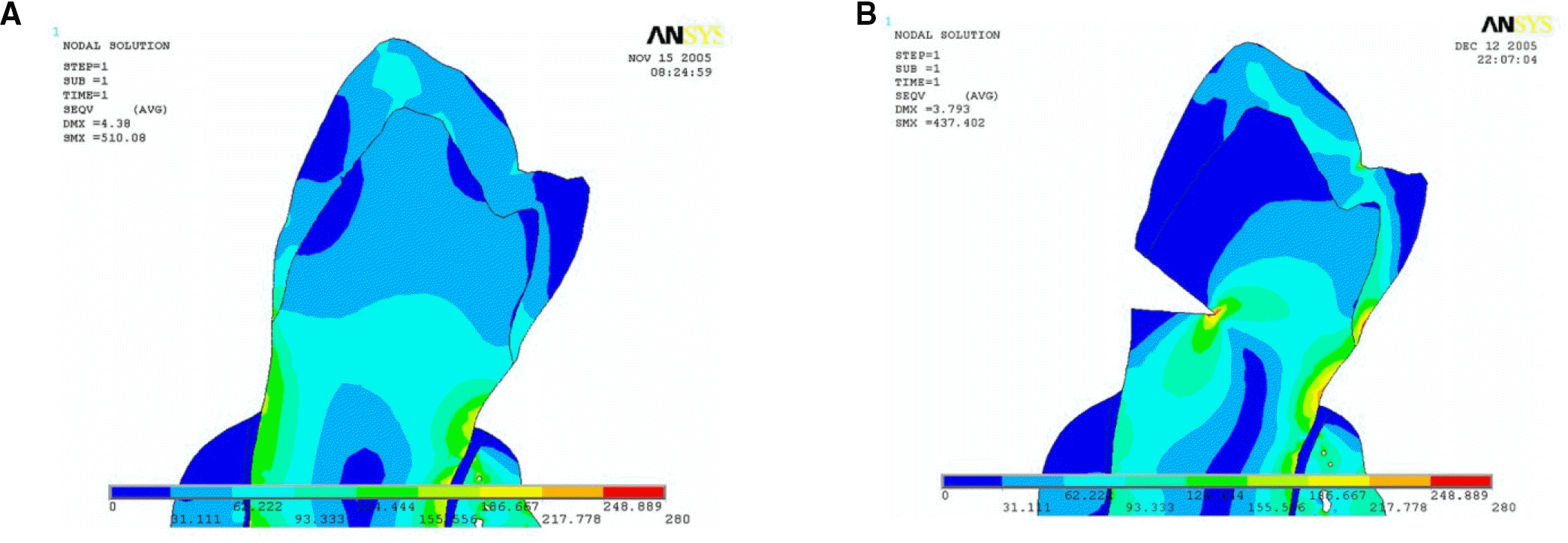Fig. 5.

von Mises stress distribution of normal tooth and the tooth with abfraction lesion. (A) Normal tooth, (B) Tooth with abfraction lesion.

Fig. 6.

von Mises stress distribution in the case that the finish line of metal-ceramiccrown is set just at the lower border of wedge-shaped defect.

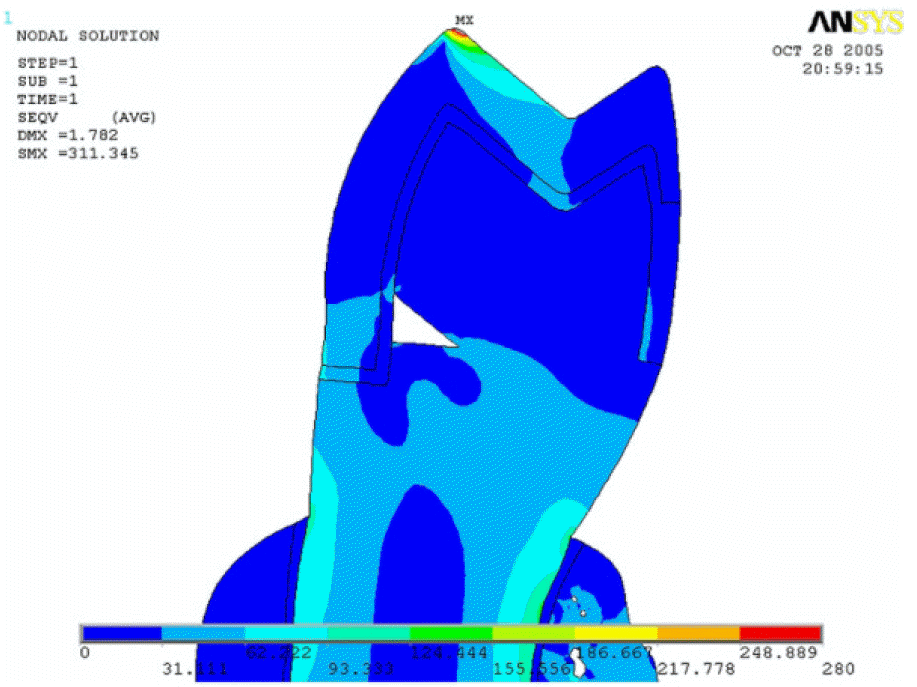Fig. 7.

von Mises stress distribution in the case that the finish line of metal-ceramic crown is set 1 mm below the lower border of wedge-shaped defect.

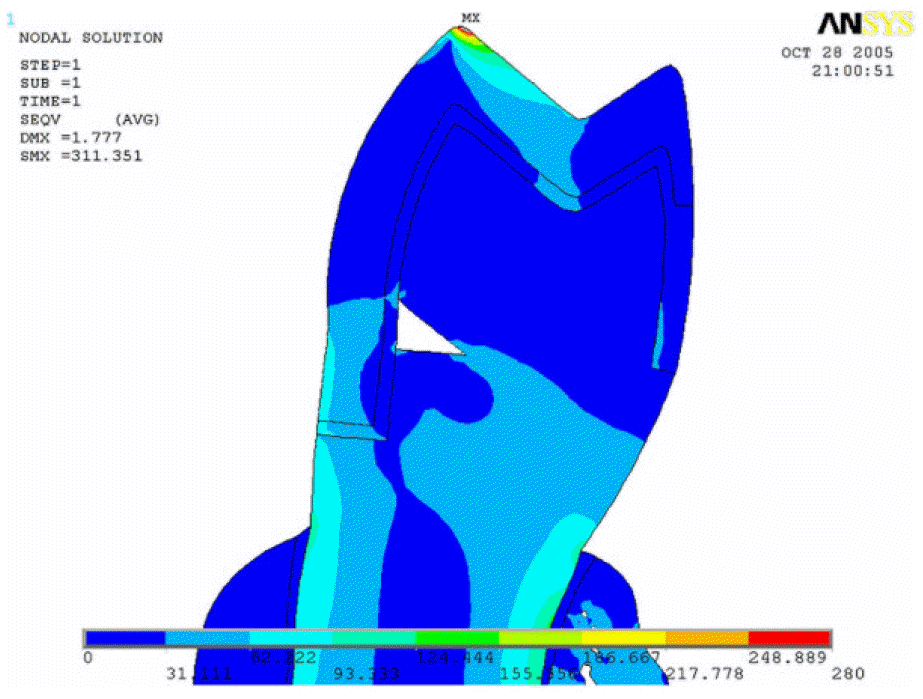Fig. 8.

von Mises stress distribution in the case that the finish line of metal-ceramic crown is set 2 mm below the lower border of wedge-shaped defect.

Table 1.

Material properties used in the finite element analysis

Materials	Young's Modulus (MPa)	Poisson's ratio	Reference
Enamel	80,000	0.30	Rees³
Dentin	15,000	0.31	Rees³
PDL	50	0.49	Rees and Jacobsen¹⁴
Cortical bone	13,800	0.26	Vincent¹⁵
Cancellous bone	345	0.30	Rees³
Type III gold	80,000	0.33	Lewinstein¹⁶
Ceramic	68,900	0.28	Lewinstein¹⁶

TOOLS

Similar articles