Abstract
Purpose
The aim of this study was to evaluate the stress concentration and distribution whether restoring the cavity or not while restoring with metal ceramic crown on tooth with abfraction lesion using finite element analysis.
Materials and methods
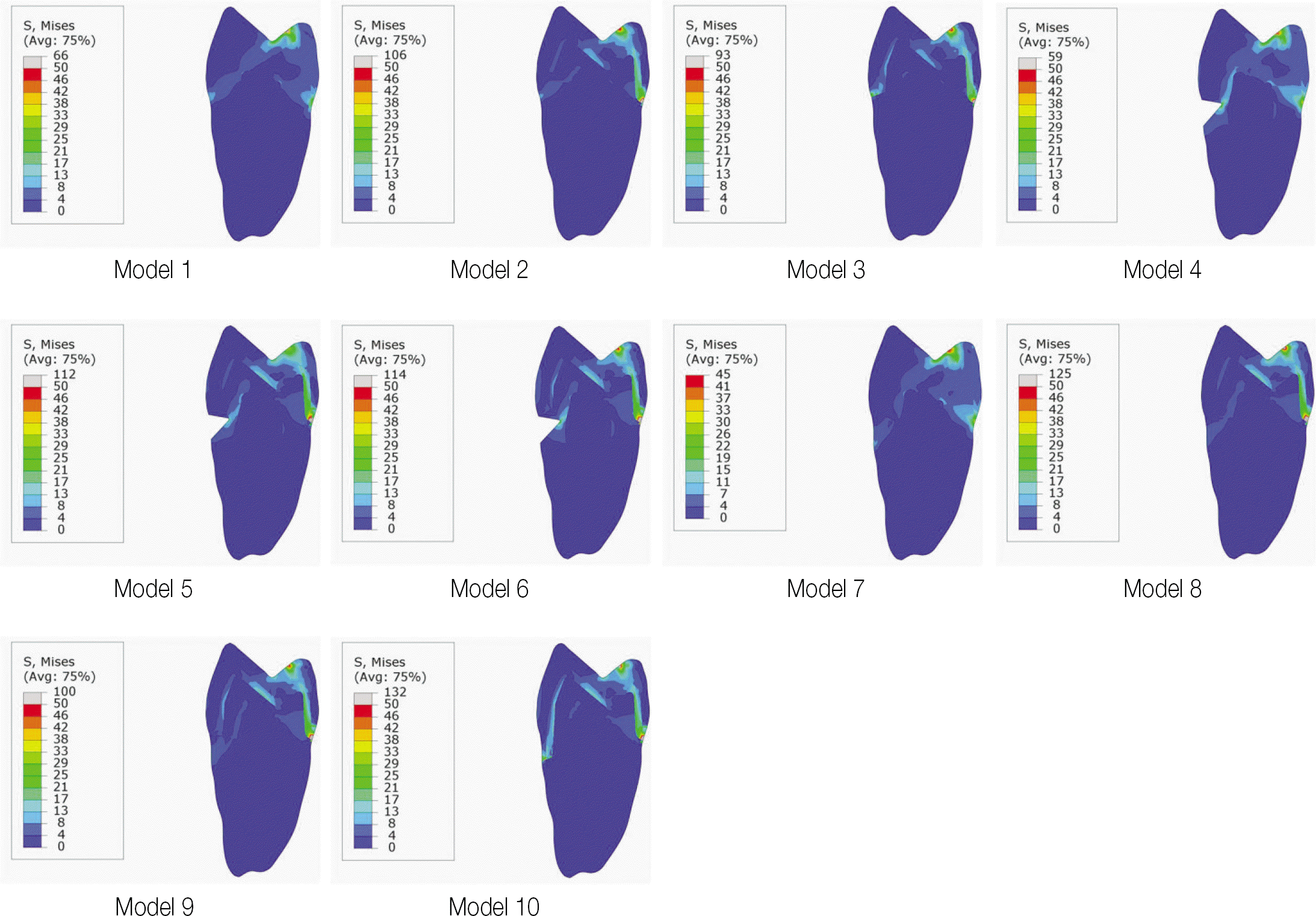
Maxillary first premolar was selected and made a total of 10 finite element model. Model 1 was natural tooth; Model 2 was tooth with metal ceramic crown restoration which margin was positioned above 2 mm from CEJ; Model 3 was tooth with metal ceramic crown restoration which margin was positioned on CEJ; Model 4 was natural tooth which has abfraction lesion; Model 5 and 6 had abfraction lesion and the other condition was same as model 2 and 3, respectively; Model 7 was natural tooth which had abfraction lesion restored with composite resin; Model 8 and 9 was tooth with metal ceramic crown after restoring on abfraction lesion with composite resin; Model 10 was restored tooth on abfraction lesion with composite resin and metal ceramic crown restoration which margin is positioned on lower border of abfraction lesion. Load A and Load B was also designed. Von Mises value was evaluated on each point.
Go to : 
REFERENCES
1. McCoy G. The etiology of gingival erosion. J Oral Implantol. 1982; 10:361–2.
2. Lee WC, Eakle WS. Possible role of tensile stress in the etiology of cervical erosive lesions of teeth. J Prosthet Dent. 1984; 52:374–80.

3. Grippo JO. Abfractions: a new classification of hard tissue lesions of teeth. J Esthet Dent. 1991; 3:14–9.

4. Nohl FS, McCabe JF, Walls AWG. The effect of load angle on strains induced in maxillary premolars in vitro. J Dent Res. 1999; 78:1059.
5. Lambrechts P, Braem M, Vanherle G. Buonocore memorial lecture. Evaluation of clinical performance for posterior composite resins and dentin adhesives. Oper Dent. 1987; 12:53–78.
7. Burke FJ, Whitehead SA, McCaughey AD. Contemporary concepts in the pathogenesis of the Class V non-carious lesion. Dent Update. 1995; 22:28–32.
8. Rees JS, Jacobsen PH. Modelling the effects of enamel anisotropy with the finite element method. J Oral Rehabil. 1995; 22:451–4.
9. Pintado MR, Delong R, Ko CC, Sakaguchi RL, Douglas WH. Correlation of noncarious cervical lesion size and occlusal wear in a single adult over a 14-year time span. J Prosthet Dent. 2000; 84:436–43.

10. Telles D, Pegoraro LF, Pereira JC. Prevalence of noncarious cervical lesions and their relation to occlusal aspects: a clinical study. J Esthet Dent. 2000; 12:10–5.

11. Dejak B, Mlotkowski A, Romanowicz M. Finite element analysis of mechanism of cervical lesion formation in simulated molars during mastication and parafunction. J Prosthet Dent. 2005; 94:520–9.

12. Spranger H. Investigation into the genesis of angular lesions at the cervical region of teeth. Quintessence Int. 1995; 26:149–54.
13. Rees JS. A review of the biomechanics of abfraction. Eur J Prosthodont Restor Dent. 2000; 8:139–44.
14. Tanaka M, Naito T, Yokota M, Kohno M. Finite element analysis of the possible mechanism of cervical lesion formation by occlusal force. J Oral Rehabil. 2003; 30:60–7.

15. Borcic J, Anic I, Smojver I, Catic A, Miletic I, Ribaric SP. 3D finite element model and cervical lesion formation in normal occlusion and in malocclusion. J Oral Rehabil. 2005; 32:504–10.

16. Piotrowski BT, Gillette WB, Hancock EB. Examining the prevalence and characteristics of abfractionlike cervical lesions in a population of U.S. veterans. J Am Dent Assoc. 2001; 132:1694–701.

17. Goel VK, Khera SC, Ralston JL, Chang KH. Stresses at the dentinoenamel junction of human teeth-a finite element investigation. J Prosthet Dent. 1991; 66:451–9.

18. Rees JS, Hammadeh M, Jagger DC. Abfraction lesion formation in maxillary incisors, canines and premolars: a finite element study. Eur J Oral Sci. 2003; 111:149–54.

19. Robinson C, Kirkham J, Brookes SJ, Shore RC. Chemistry of Mature enamel. Dental enamel-formation to destruction. Robinson C, Kirkham J, Sore RC, editors. CRC Press;Boca Raton; FL: 1995. p. 137.
20. Meredith N, Sherriff M, Setchell DJ, Swanson SA. Measurement of the microhardness and Young's modulus of human enamel and dentine using an indentation technique. Arch Oral Biol. 1996; 41:539–45.

21. Goel VK, Khera SC, Ralston JL, Chang KH. Stresses at the dentinoenamel junction of human teeth-a finite element investigation. J Prosthet Dent. 1991; 66:451–9.

22. Poole DF, Newman HN, Dibdin GH. Structure and porosity of human cervical enamel studied by polarizing microscopy and transmission electron microscopy. Arch Oral Biol. 1981; 26:977–82.

23. Scott JH, Symons NBB. Introduction to dental anatomy. 9th ed.Edinburgh: Churchill Livingstone; UK;1982.
24. Braem M, Lambrechts P, Vanherle G. Stress-induced cervical lesions. J Prosthet Dent. 1992; 67:718–22.

25. Borcic J, Anic I, Urek MM, Ferreri S. The prevalence of non-carious cervical lesions in permanent dentition. J Oral Rehabil. 2004; 31:117–23.

26. Kim HJ, Kim SJ, Choi JI, Lee JY. Effects of non-carious cervical lesions and class V restorations on periodontal conditions. J Korean Acad Periodontol. 2009; 39:17–26.

27. Spears IR. A three-dimensional finite element model of prismatic enamel: a re-appraisal of the data on the Young's modulus of enamel. J Dent Res. 1997; 76:1690–7.

28. Vasudeva G, Bogra P, Nikhil V, Singh V. Effect of occlusal restoration on stresses around class V restoration interface: a finite-element study. Indian J Dent Res. 2011; 22:295–302.

29. Vandewalle KS, Vigil G. Guidelines for the restoration of Class V lesions. Gen Dent. 1997; 45:254–60.
30. N S, N M, Shetty A, Kumari A, Dn N. Finite element analysis of stress concentration in Class V restorations of four groups of restorative materials in mandibular premolar. J Conserv Dent. 2008; 11:121–6.

31. Peumans M, De Munck J, Van Landuyt KL, Kanumilli P, Yoshida Y, Inoue S, Lambrechts P, Van Meerbeek B. Restoring cervical lesions with flexible composites. Dent Mater. 2007; 23:749–54.

32. Rees JS, Hammadeh M. Undermining of enamel as a mechanism of abfraction lesion formation: a finite element study. Eur J Oral Sci. 2004; 112:347–52.

33. Kuroe T, Itoh H, Caputo AA, Konuma M. Biomechanics of cervical tooth structure lesions and their restoration. Quintessence Int. 2000; 31:267–74.
34. Um CM, Kwon HC, Son HH, Cho BH, Rim YI. Finite element analysis of stress distribution according to cavity design of class v composite resin filling. J Korean Acad Conserv Dent. 1999; 24:67–75.
Go to : 
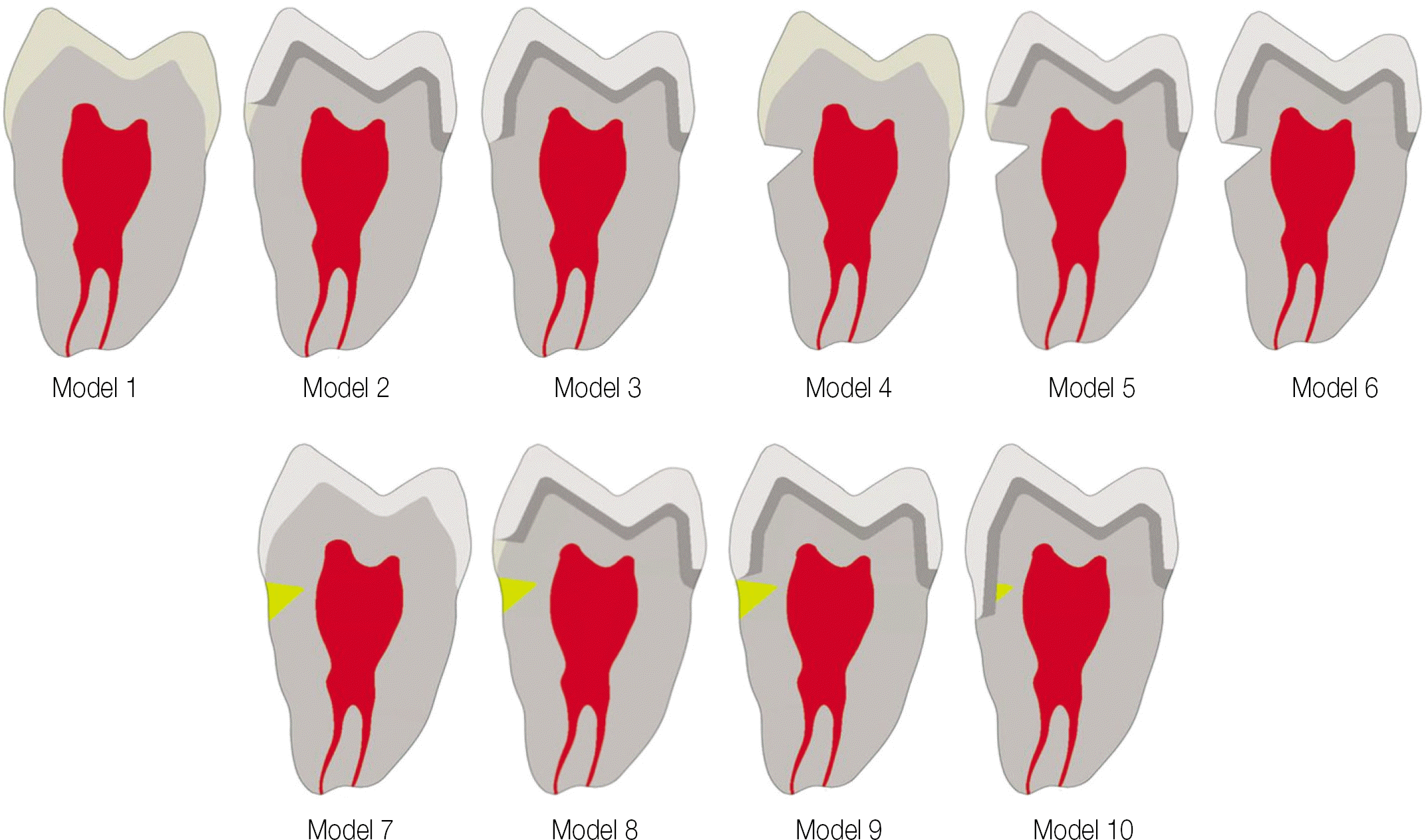 | Fig. 2.Analysis models were designed according to the experimental conditions (Parts shown with the yellow represent composite resin restorations). |
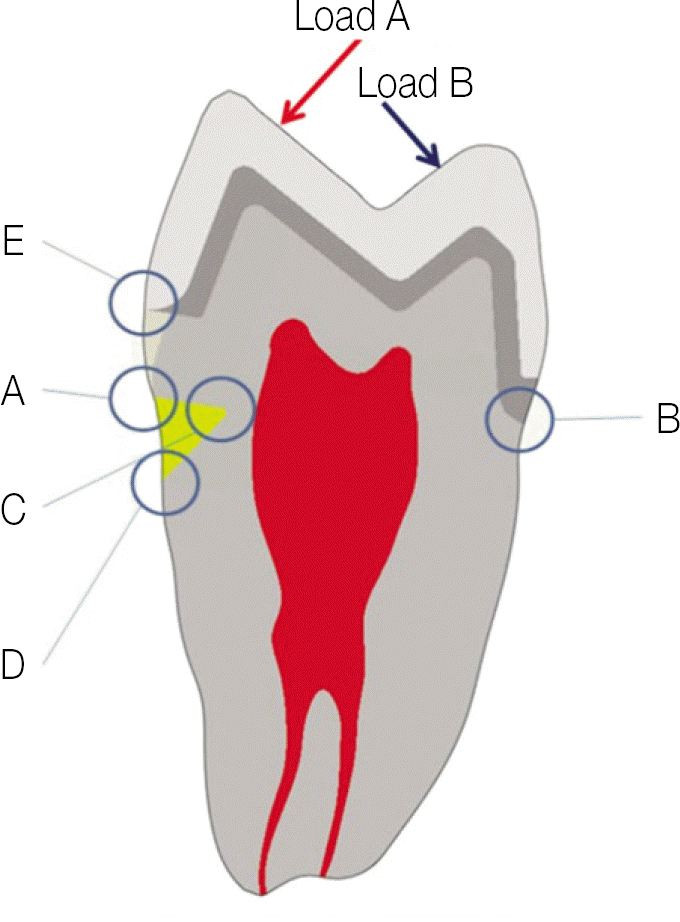 | Fig. 3.Reference points for comparison of stress value and the direction and application point of Load A and B (A: buccalcemento-enamel junction, B: palatal cemen-to-enamel junction, C: the apex of abfraction lesion, D: the apical border of abfraction lesion, E: the buccal margin of metal ceramic crown which is positioned 2 mm above from buccal CEJ, The red arrow means Load A & the blue arrow means Load B). |
Table 1.
Young's modulus and Poisson's ratio used in this study
| Young's modulus | Poisson's ratio | |
|---|---|---|
| Enamel | Exx = 80 GPa | |
| Eyy = Ezz =20 GPa | ||
| Dentin | 15 GPa | 0.31 |
| Pulp | 2.1 MPa | 0.45 |
| Composite resin | 10 GPa | 0.24 |
| Porcelain | 69 GPa | 0.28 |
| Metal | 218 GPa | 0.33 |
Table 2.
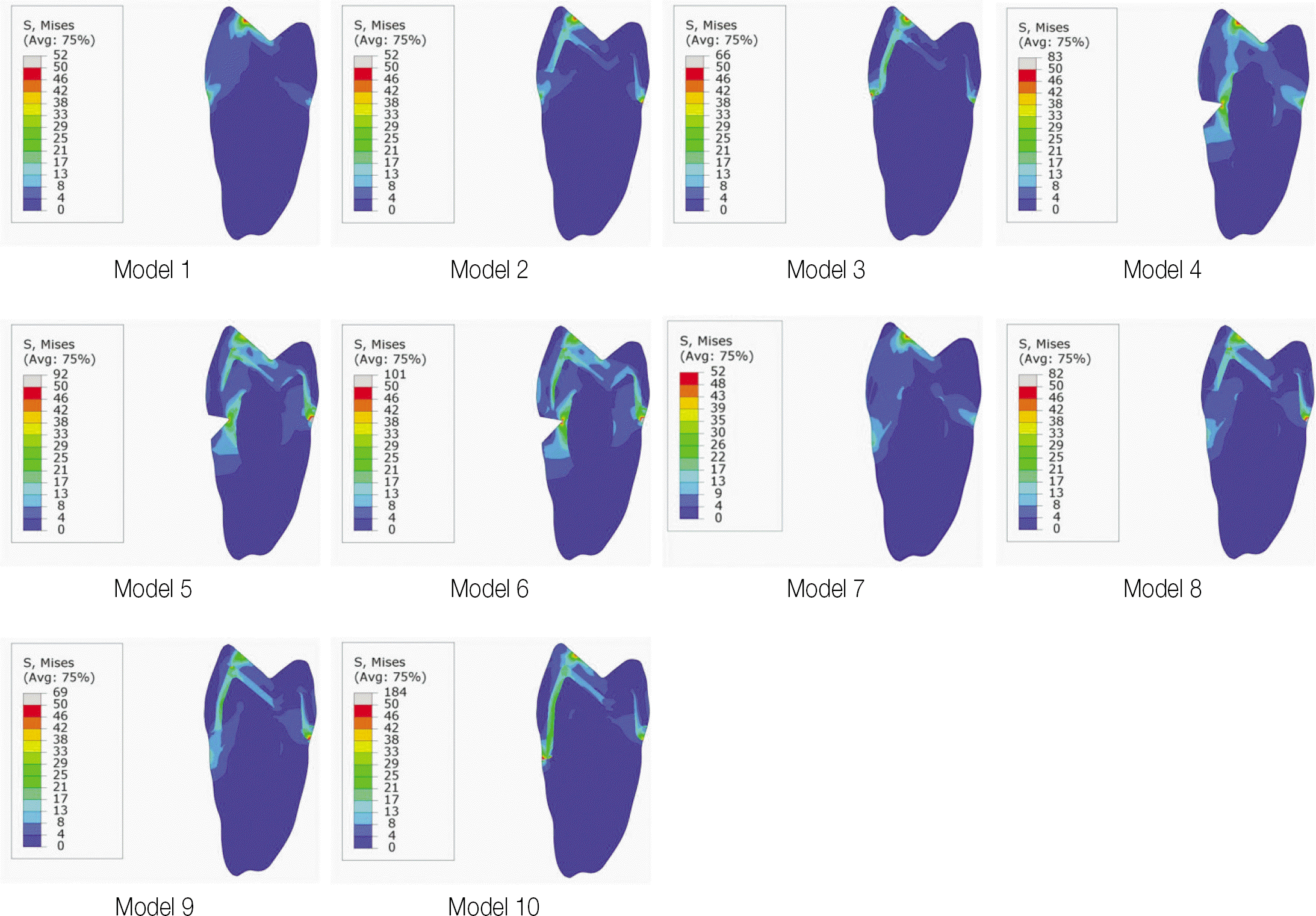
Von Mises stress values at the reference point by each load (MPa)




 PDF
PDF ePub
ePub Citation
Citation Print
Print


 XML Download
XML Download