Finite Element Analysis for Comparison of Spinous Process Osteotomies Technique with Conventional Laminectomy as Lumbar Decompression Procedure

Ho-Joong Kim; Heoung-Jae Chun; Kyoung-Tak Kang; Hwan-Mo Lee; Bong-Soon Chang; Choon-Ki Lee; Jin S. Yeom

doi:10.3349/ymj.2015.56.1.146

Journal List > Yonsei Med J > v.56(1) > 1031642

Go to TopGo to Top Go to BottomGo to Bottom

This article has been corrected. See "Erratum to "Finite Element Analysis for Comparison of Spinous Process Osteotomies Technique with Conventional Laminectomy as Lumbar Decompression Procedure" by Kim HJ, et al. (Yonsei Med J 2015;56:146-53.)" in Volume 57 on page 1051.

TOOLS

Kim, Chun, Kang, Lee, Chang, Lee, and Yeom: Finite Element Analysis for Comparison of Spinous Process Osteotomies Technique with Conventional Laminectomy as Lumbar Decompression Procedure

Original Article

Orthopedics

Yonsei Medical Journal 2015; 56(1): 146-153.

Published online: 10 December 2014

DOI: https://doi.org/10.3349/ymj.2015.56.1.146

Finite Element Analysis for Comparison of Spinous Process Osteotomies Technique with Conventional Laminectomy as Lumbar Decompression Procedure

Ho-Joong Kim^1,^*, Heoung-Jae Chun^2,^*, Kyoung-Tak Kang², Hwan-Mo Lee³, Bong-Soon Chang⁴, Choon-Ki Lee⁴, Jin S. Yeom¹

¹Spine Center and Department of Orthopedic Surgery, Seoul National University College of Medicine, Seoul National University Bundang Hospital, Seongnam, Korea.

²Department of Mechanical Engineering, Yonsei University, Seoul, Korea.

³Department of Orthopedic Surgery, Yonsei University College of Medicine, Seoul, Korea.

⁴Department of Orthopedic Surgery, Seoul National University College of Medicine, Seoul National University Hospital, Seoul, Korea.

Corresponding author: Dr. Jin S. Yeom, Spine Center and Department of Orthopedic Surgery, Seoul National University College of Medicine, Seoul National University Bundang Hospital, 82 Gumi-ro 173beon-gil, Bundang-gu, Seongnam 463-707, Korea. Tel: 82-31-787-7195, Fax: 82-31-787-4056, highcervical@gmail.com

Equal contributor:

*Ho-Joong Kim and Heoung-Jae Chun contributed equally to this work.

Received 6 February 2014 Revised 23 March 2014 Accepted 31 March 2014

(open-access):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Purpose

The purpose of this study was to evaluate and compare the biomechanical behavior of the lumbar spine after posterior decompression with the spinous process osteotomy (SPiO) technique or the conventional laminectomy (CL) technique using a finite element (FE) model.

Materials and Methods

Three validated lumbar FE models (L2-5) which represented intact spine and two decompression models using SPiO and CL techniques at the L3-4 segment were developed. In each model, the ranges of motion, the maximal von Mises stress of the annulus fibrosus, and the intradiscal pressures at the index segment (L3-4) and adjacent segments (L2-3 and L4-5) under 7.5 Nm moments were analyzed. Facet contact forces were also compared among three models under the extension and torsion moments.

Results

Compared to the intact model, the CL and SPiO models had increased range of motion and annulus stress at both the index segment (L3-4) and the adjacent segments under flexion and torsion. However, the SPiO model demonstrated a reduced range of motion and annulus stress than the CL model. Both CL and SPiO models had an increase of facet contact force at the L3-4 segment under the torsion moment compared to that of the intact model. Under the extension moment, however, three models demonstrated a similar facet contact force even at the L3-4 model.

Conclusion

Both decompression methods lead to postoperative segmental instability compared to the intact model. However, SPiO technique leads to better segmental stability compared to the CL technique.

Keywords: Lumbar spinal stenosis, spinous process osteotomies, conventional laminectomy, finite element model

INTRODUCTION

Degenerative lumbar stenosis (DLS) is a common condition in degenerative spines involving a narrowing of the spinal canal, producing radiculopathy or claudication.1 Although DLS is not a life-threatening disease, it significantly affects quality of life, especially in elderly patients.2 As such, DLS is the most common indication for spinal surgery in the geriatric population.3 Proper surgical treatment, such as decompression with or without fusion, have been reported to be very promising, alleviating intractable back pain and radiating pain or claudication.3,4

The surgical treatment of DLS has undergone a gradual evolution from traditional laminectomy, which includes the sacrifice of posterior elements such as the lamina, spinous processes, and posterior ligament complex (PLC), as well as minimally invasive techniques. A recent trend in the surgical treatment of DLS is the preservation of posterior elements to maintain integrity and segmental stability and simultaneously to allow for sufficient decompression of neural structures in the spinal canal.5 However, because of its minimally invasive nature, this type of surgery has several disadvantages, including potentially limited exposure, a demanding learning curve, and expensive instruments.6,7

Weiner, et al.8 first introduced the spinous process osteotomy (SPiO) technique for lumbar canal decompression, which involves osteotomy of spinous processes at their bases at the decompressed level. This technique affords excellent visualization while minimizing the destruction of tissues not directly involved in the pathologic process.8,9 The SPiO technique can also be used to treat multilevel stenotic lesions of the lumbar spine.9 However, the biomechanical consequences of SPiO are poorly understood, and no previous studies have investigated whether the sacrifice of the posterior spinous processes could increase the risk of segmental instability, despite preservation of the supraspinous and interspinous ligaments.

Furthermore, after decompression surgery without fusion, postoperative segmental stability is of paramount concern, given that postoperative segmental instability leads to the deterioration of surgical outcomes, which in turn may require another surgical stabilizing procedure, such as fusion. Therefore, the purpose of this study was first to assess the biomechanics of the spine after SPiO with respect to range of motion, disc stress, and facet contact forces and then to compare them to the biomechanics after conventional laminectomy (CL). Lastly, we evaluated the significance of the preservation of PLC for postoperative segmental stability, using finite element (FE) analysis.

MATERIALS AND METHODS

An FE model of the intact lumbar spine (L2-5)

We developed a three-dimensional (3D) nonlinear FE model of the lumbar spine that consisted of four lumbar vertebrae, three intervertebral discs, and the associated spinal ligaments. Geometrical details of the human lumbar spine (L2-5) were obtained from high-resolution computed tomography (CT) images of a 46-year-old male subject who had no spinal deformities. Digital CT data were imported to a software program (Mimics; Materialise Inc., Leuven, Belgium) that was used to generate the 3D geometrical surface of the lumbar spine. Initial Graphic Exchange System files exported from Mimics were input into Unigraphics NX 3.0 (Siemens PLM Software, Torrance, CA, USA) to form solid models for each vertebral segment. The solid model was then imported into Hypermesh 8.0 (Altair Engineering, Inc., Troy, MI, USA) to generate FE meshes. In the current FE model, the hexa mesh was generated for the entire area. The FE method was analyzed with commercially available software (ABAQUS 6.11-1; Hibbitt, Karlsson and Sorenson, Inc., Providence, RI, USA).

3D homogenous and transversely isotropic solid elements were used to model the cortical and cancellous cores, the posterior bony parts of the vertebrae. The anterior longitudinal ligament, posterior longitudinal ligament, intertransverse ligament, ligamentum flavum, capsular ligament, interspinous ligament, and supraspinous ligament were modeled using tension-only truss elements.

Material properties

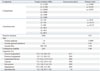
Material properties were selected from various sources in the literature (Table 1).10,11,12,13 The cortical and cancellous regions of the vertebrae were modeled independently. Differentiation between cortical and trabecular bone in the posterior region was difficult to delineate; therefore, the posterior elements were all assigned a single set of material properties

The annulus fibrosus was modeled as a composite of a solid matrix with embedded fibers (using the REBAR parameter) in concentric rings surrounding a nucleus pulposus, which was considered to be an incompressible inviscid fluid. Element members with hybrid formulation (C3D8H) combined with low elastic modulus and large Poisson ratio definitions were applied to simulate the nucleus pulposus. Eight-node brick elements were employed to model the matrix of the ground substance. Each of the four concentric rings of ground substance contained two evenly spaced layers of annulus fibers oriented at ±30° to horizontal. The reinforcement structure annulus fibers were represented by truss elements with modified tension-only elasticity. In the radial direction, four double cross-linked fiber layers were defined, and those fibers were bounded by the annulus ground substance and both endplates. In addition, these fibers had proportionally decreasing elastic strength from the outermost (550 MPa) to the innermost (358 MPa) layers.14,15

Naturally changing ligament stiffness was simulated thro-ugh a hypoelastic material designation, in which stiffness was initially less at lower strains but increased at higher strains (Table 1). Three-dimensional truss elements were used to simulate ligaments, which were active only in tension.

Simulation of SPiO and CL

In order to simulate the SPiO model, the spinous processes of L3 and L4 were osteotomized at their bases in the model of the intact spine (L2-5), while the interspinous ligaments and supraspinous ligaments between L3 and L4 was left intact. Decompression, including partial laminectomy and removal of the ligamentum flavum of L3-4 was then performed. To simulate the CL model, the distal half of the L3 spinous process and the proximal half of the L4 spinous process were cut, along with the supraspinous and interspinous ligaments between L3 and L4, followed by decompression procedures, including partial laminectomy and removal of the ligamentum flavum of L3-4 (Fig. 1).

Boundary and loading conditions

This FE investigation included two types of loading conditions corresponding to 1) loads used in the experimental studies for model validation16,17,18 and 2) model predictions for clinically relevant loading scenarios. The validation of the current model was described in the previous study.19 The second type of loading condition was the load control protocol. The follower load technique was used to simulate the vector sum of trunk muscle co-activation by a single internal force vector that acted tangentially to the curvature of the spine passing through each segmental center of rotation.20 This "follower" path tangential to the curvature of the spine mimicked physiologic compressive loads on the lumbar spine seen in vivo.5 The 400 N compressive follower load was simulated at each motion segment in the model by a pair of 2-node thermo-isotropic truss elements. The trusses were attached bilaterally to the cortical shell of the vertebrae at each motion segment. Each truss spanned the disc space passing through the instantaneous center of rotation at each motion segment.5 This load control protocol involved the application of 7.5 Nm flexion, extension, torsion, and lateral bending pure moments to three lumbar models on the L2 vertebral body under a 400 N follower load

RESULTS

Comparison of range of motion between models

The ranges of motion at each corresponding level were compared among the SPiO, CL, and intact models and were found to exhibit a similar pattern at both index and adjacent segments under 4 moments. However, under the flexion and torsion moments, the CL model had the greatest increase in the range of motion at both the index segment and adjacent segments. The range of motion in the SPiO model was greater than that of the intact model but less than that of the CL model for each corresponding segment under the flexion and torsion moments. However, under the extension and lateral bending moments, there were no differences between any of the segments for the three models (Fig. 2).

The maximal von mises stress of the annulus fibrosus and the intradiscal pressure of the nucleus pulposus at the intervertebral disc in each model

The von Mises stress of the annulus fibrosus (AF) at the index and adjacent segments was greater in the CL and SPiO models than in the intact model under the flexion and torsion moments only, while there were few differences in the AF stress among the three models under the extension and lateral bending moments. The change in the AF stress under the flexion moment was a 180% increase in the CL model and a 110% increase in the SPiO model compared to the intact model. The change in the AF stress under the torsional moment was 18% greater than the intact model in the CL model and 9% greater in the SPiO model (Figs. 3 and 4). Under the flexion moment, there was a 12.9% increase of the AF stress at the proximal adjacent segments (L2-3) in the CL model and a 6.5% increase in the SPiO model. There was a 20.7% increase in AF stress at the distal adjacent segments under the flexion moment in the CL model and a 13.8% increase in the SPiO model (Figs. 3 and 4). The changes in intradiscal nucleus pulposus (NP) pressure showed a similar trend to that of AF stress.

Comparison of facet contact force among the three models

The increase in facet contact force under the extension moment was not significantly different among three models. However, the change in facet contact force under the torsion moment was 68.6% greater in the CL model and 58.8% greater in the SPiO model. The change in facet contact force was 3.2% greater at the proximal adjacent segments and 10.5% greater at the distal adjacent segments under the torsion moment in both the CL and SPiO models (Fig. 5).

DISCUSSION

Conventional laminectomy requires the sacrifice of the supraspinous and interspinous ligament complexes, which normally act as a tension band in the flexion moment. Therefore, after conventional laminectomy, the lumbar spine structure may be vulnerable to segmental instability at the operated segment, especially in the flexion moment. As expected, in the current study, the CL model had a larger range of motion than the intact model at the level of decompression under the flexion and torsion moments. However, the SPiO model, in which the PLC was preserved, had less motion than the CL model but greater motion than the intact model at the operated level (L3-4) under both the flexion and torsion moments. These results suggest that the SPiO model provides better postoperative segmental stability than the CL model due to the preservation of the PLC, which might help protect the index segment under both the flexion and torsion moments. The previous studies corroborate the current findings, reporting that both supraspinous ligaments and interspinous ligaments act as a tension band in the flexion moment,21,22 and the interconnections between the supraspinous and interspinous ligaments were shown to resist the peak flexion moment more than the facet joint complexes, the intervertebral disc, and the ligamentum flavum in the porcine lumbar spine model.23

In the current study, the results for annulus stress were consistent with those for the range of motion. Compared to the intact model, the CL model demonstrated a 180% increase in annulus stress under the flexion moment and an 18% increase under the torsion moment, while the SPiO model demonstrated an increase of 110% under the flexion moment valiand 9% under the torsion moment. Under the extension and lateral bending moments, there were few differences of AF stress among three models. The change in the intradiscal NP pressure exhibited a similar trend to that of the annulus stress. These results highlight two important biomechanical features of the SPiO and CL techniques. First, the preservation of the PLC does provide resistance to the flexion moment and also has a tension band effect on the torsion moment. Although the SPiO technique produced a considerable increase in AF stress under the flexion and torsion moments compared to the intact model, this value was nearly half that of the CL model. Thus, it appears as though the SPiO technique has the advantage of better postoperative segmental stability than the CL technique under the flexion and torsion moments. Second, medial one-third facetectomy for decompression does not cause postoperative instability under the extension and lateral bending moments at the operated segment, which agree with previous studies.24,25

Another result of this study was that the facet contact force increased considerably under the torsion moment in both the CL and SPiO models compared to the intact model. Biomechanically, the facet joints share the load during compression and extension of the lumbar spine and protect the disc against torsion.26 Therefore, the facet contact force generally increases under the extension and torsion moments. The present study showed little increase of the facet contact force under the extension moment, with 68.6% and 58.8% increments of facet contact force under torsion in the CL and SPiO models, respectively, compared to the intact model. This finding can be explained by the fact that two facet joints evenly and simultaneously resist or share the load under the extension moment. Although the medial one-third of the facet joints was removed in both the CL and SPiO models, the load might have been shared evenly on each side of the facet joints under the extension moment, leading to a facet contact force that was similar to that of the intact model. This is consistent with the generally held belief that medial one-third facetectomy does not cause postoperative segmental instability after decompression.25 In contrast, under the torsion moment, the load was transmitted to only one facet joint on the rotation side, which led to a marked increase in the facet contact force on that side. Furthermore, the similar increment of facet contact force between the CL and SPiO models under the torsion moment implies that preservation of the PLC does not protect the facet joint. In addition, the notable increase in the facet contact force after decompression in both the CL and SPiO models can explain why the recurrence rates of facet cysts differ between decompression with and without fusion.27,28 Given that facet cysts are associated with degenerative changes, the markedly increased facet contact force after decompression surgery might be a cause of the development or recurrence of facet cysts.

Interestingly, the continuity of the PLC affected both the operated segments and the adjacent segments. Under the flexion moment, the AF stress at the proximal (L2-3) adjacent segment increased by 13.0% in the CL model and 9.8% in the SPiO model; at the distal (L4-5) adjacent segment, the increases of AF stress were 20.7% for the CL model and 13.8% for the SPiO model. These findings indicate that decompression surgery may also have an adverse effect on the adjacent segments. In addition, the finding that the change in AF stress at the adjacent segments was less in the SPiO model than in the CL model implies that the preservation of the PLC also had a protective effect on AF stress at the adjacent segments in the SPiO model. To aggregate, the continuity of the PLC seems to be of paramount importance both at the index segment and the adjacent segments due to the integral role of the PLC as a tension band for the whole lumbar spine.

It is acknowledged that this study has some limitations. We did not simulate degenerative changes in the lumbar models; however, almost all patients with DLS who undergo decompression surgery have disc degeneration at the corresponding segment, and this degeneration alters biomechanics.29,30 Future studies should assess the impact of disc degeneration in order to precisely determine the effects of graded removal of the posterior elements, such as the lamina, facet joint, and ligaments. Nonetheless, FE studies fundamentally require assumptions and simplifications concerning the applied loads and the geometry and material properties of different tissues, and we believe the trends we observed with regard to stress differences between the validated models have relevance to the clinical in vivo state. Furthermore, we were able to extract data regarding intrinsic parameters (e.g., facet load, stress, strain, etc.) related to decompression procedures using FE analysis, whereas a major limitation of cadaver studies is the inability to determine these intrinsic parameters.

In conclusion, both decompression methods lead to postoperative segmental instability compared to the intact model. However, the SpiO technique leads to better segmental stability compared to the CL technique. Therefore, preservation of the PLC in the SPiO technique may help reduce disc stress under both flexion and torsion moments, while the facet contact force appears less dependent on the decompression technique.

Figures and Tables

Fig. 1

Finite element models. (A) Conventional laminectomy (CL) model; arrow indicates the sacrifice of posterior ligament complex. (B) Spinous process osteotomy (SPiO) model; arrow indicates the preservation of posterior ligament complex.

Fig. 2

Comparison between the three models of the range of motion at each segment for the four moments. CL, conventional laminectomy; SPiO, spinous process osteotomy.

Fig. 3

Comparison of the maximal von Mises stress of the annulus fibrosus and the intradiscal pressure of the nucleus pulposus among three models. (A) Comparison of the maximal von Mises stress of the annulus fibrosus (MPa). (B) Comparison of intradiscal pressure of the nucleus pulposus.

Fig. 4

Distribution of stress of the annulus fibrosus in the CL and SPiO models under flexion and torsion moment. (A) CL model under flexion. (B) SPiO model under flexion. (C) CL model under torsion. (D) SPiO model under torsion. CL, conventional laminectomy; SPiO, spinous process osteotomy.

Fig. 5

Comparison of the facet contact force among 3 models. CL, conventional laminectomy; SPiO, spinous process osteotomy.

Table 1

Material Properties in the Present FE Models

Component	Young's modulus (MPa)	Cross-section (mm²)	Poisson's ratio
Cortical bone	E_x=11300		υ_xy=0.484
	E_y=11300		υ_xz=0.203
	E_z=22000		υ_yz=0.203
	G_x=3800
	G_y=5400
	G_z=5400
Cancellous bone	E_x=140		υ_xy=0.45
	E_y=140		υ_xz=0.315
	E_z=200		υ_yz=0.315
	G_x=48.3
	G_y=48.3
	G_z=48.3
Posterior elements	3500		0.25
Disc
Nucleus pulposus	1.0		0.4999
Annulus (ground substance)	4.2		0.45
Annulus fiber	358-550		0.30
Cartilaginous endplate	24.0		0.40
Ligaments (%)
Anterior longitudinal	7.8 (<12), 20 (>12)	63.7
Posterior longitudinal	10 (<11), 20 (>11)	20.0
Ligamentum flavum	15 (<6.2), 19.5 (>6.2)	40.0
Capsular	7.5 (<25), 32.9 (>25)	30.0
Interspinous	10 (<14), 11.6 (>14)	40.0
Supraspinous	8.0 (<20), 15 (>20)	30.0
Intertransverse	10 (<18), 58.7 (>18)	1.8

FE, finite element.

ACKNOWLEDGEMENTS

This study was supported by a grant from Dong-A Pharm. Co.

Notes

The authors have no financial conflicts of interest.

References

1. Verbiest H. A radicular syndrome from developmental narrowing of the lumbar vertebral canal. J Bone Joint Surg Br. 1954; 36-B:230–237.

2. Hilibrand AS, Rand N. Degenerative lumbar stenosis: diagnosis and management. J Am Acad Orthop Surg. 1999; 7:239–249.

3. Sengupta DK, Herkowitz HN. Lumbar spinal stenosis. Treatment strategies and indications for surgery. Orthop Clin North Am. 2003; 34:281–295.

4. Atlas SJ, Keller RB, Wu YA, Deyo RA, Singer DE. Long-term outcomes of surgical and nonsurgical management of lumbar spinal stenosis: 8 to 10 year results from the maine lumbar spine study. Spine (Phila Pa 1976). 2005; 30:936–943.

5. Bresnahan L, Ogden AT, Natarajan RN, Fessler RG. A biomechanical evaluation of graded posterior element removal for treatment of lumbar stenosis: comparison of a minimally invasive approach with two standard laminectomy techniques. Spine (Phila Pa 1976). 2009; 34:17–23.

6. Ikuta K, Tono O, Tanaka T, Arima J, Nakano S, Sasaki K, et al. Surgical complications of microendoscopic procedures for lumbar spinal stenosis. Minim Invasive Neurosurg. 2007; 50:145–149.

7. Yuzawa Y. The interspinous ligament should be removed for the decompression surgery with the case of lumbar spinal canal stenosis. Arch Orthop Trauma Surg. 2011; 131:753–758.

8. Weiner BK, Fraser RD, Peterson M. Spinous process osteotomies to facilitate lumbar decompressive surgery. Spine (Phila Pa 1976). 1999; 24:62–66.

9. El-Abed K, Barakat M, Ainscow D. Multilevel lumbar spinal stenosis decompression: midterm outcome using a modified hinge osteotomy technique. J Spinal Disord Tech. 2011; 24:376–380.

10. Shirazi-Adl SA, Shrivastava SC, Ahmed AM. Stress analysis of the lumbar disc-body unit in compression. A three-dimensional nonlinear finite element study. Spine (Phila Pa 1976). 1984; 9:120–134.

11. Pintar FA, Yoganandan N, Myers T, Elhagediab A, Sances A Jr. Biomechanical properties of human lumbar spine ligaments. J Biomech. 1992; 25:1351–1356.

12. Goel VK, Kim YE, Lim TH, Weinstein JN. An analytical investigation of the mechanics of spinal instrumentation. Spine (Phila Pa 1976). 1988; 13:1003–1011.

13. Wu HC, Yao RF. Mechanical behavior of the human annulus fibrosus. J Biomech. 1976; 9:1–7.

14. Shirazi-Adl A, Ahmed AM, Shrivastava SC. Mechanical response of a lumbar motion segment in axial torque alone and combined with compression. Spine (Phila Pa 1976). 1986; 11:914–927.

15. Polikeit A, Ferguson SJ, Nolte LP, Orr TE. Factors influencing stresses in the lumbar spine after the insertion of intervertebral cages: finite element analysis. Eur Spine J. 2003; 12:413–420.

16. Renner SM, Natarajan RN, Patwardhan AG, Havey RM, Voronov LI, Guo BY, et al. Novel model to analyze the effect of a large compressive follower pre-load on range of motions in a lumbar spine. J Biomech. 2007; 40:1326–1332.

17. Schilling C, Krüger S, Grupp TM, Duda GN, Blömer W, Rohlmann A. The effect of design parameters of dynamic pedicle screw systems on kinematics and load bearing: an in vitro study. Eur Spine J. 2011; 20:297–307.

18. Wilson DC, Niosi CA, Zhu QA, Oxland TR, Wilson DR. Accuracy and repeatability of a new method for measuring facet loads in the lumbar spine. J Biomech. 2006; 39:348–353.

19. Kim HJ, Chun HJ, Lee HM, Kang KT, Lee CK, Chang BS, et al. The biomechanical influence of the facet joint orientation and the facet tropism in the lumbar spine. Spine J. 2013; 13:1301–1308.

20. Patwardhan AG, Havey RM, Meade KP, Lee B, Dunlap B. A follower load increases the load-carrying capacity of the lumbar spine in compression. Spine (Phila Pa 1976). 1999; 24:1003–1009.

21. Goel VK, Fromknecht SJ, Nishiyama K, Weinstein J, Liu YK. The role of lumbar spinal elements in flexion. Spine (Phila Pa 1976). 1985; 10:516–523.

22. Hindle RJ, Pearcy MJ, Cross A. Mechanical function of the human lumbar interspinous and supraspinous ligaments. J Biomed Eng. 1990; 12:340–344.

23. Gillespie KA, Dickey JP. Biomechanical role of lumbar spine ligaments in flexion and extension: determination using a parallel linkage robot and a porcine model. Spine (Phila Pa 1976). 2004; 29:1208–1216.

24. Natarajan RN, Andersson GB, Patwardhan AG, Andriacchi TP. Study on effect of graded facetectomy on change in lumbar motion segment torsional flexibility using three-dimensional continuum contact representation for facet joints. J Biomech Eng. 1999; 121:215–221.

25. Lee KK, Teo EC, Qiu TX, Yang K. Effect of facetectomy on lumbar spinal stability under sagittal plane loadings. Spine (Phila Pa 1976). 2004; 29:1624–1631.

26. Adams MA, Hutton WC. The effect of posture on the role of the apophysial joints in resisting intervertebral compressive forces. J Bone Joint Surg Br. 1980; 62:358–362.

27. Bydon A, Xu R, Parker SL, McGirt MJ, Bydon M, Gokaslan ZL, et al. Recurrent back and leg pain and cyst reformation after surgical resection of spinal synovial cysts: systematic review of reported postoperative outcomes. Spine J. 2010; 10:820–826.

28. Xu R, McGirt MJ, Parker SL, Bydon M, Olivi A, Wolinsky JP, et al. Factors associated with recurrent back pain and cyst recurrence after surgical resection of one hundred ninety-five spinal synovial cysts: analysis of one hundred sixty-seven consecutive cases. Spine (Phila Pa 1976). 2010; 35:1044–1053.

29. Kirkaldy-Willis WH, Farfan HF. Instability of the lumbar spine. Clin Orthop Relat Res. 1982; 110–123.

30. Galbusera F, Schmidt H, Neidlinger-Wilke C, Gottschalk A, Wilke HJ. The mechanical response of the lumbar spine to different combinations of disc degenerative changes investigated using randomized poroelastic finite element models. Eur Spine J. 2011; 20:563–571.

TOOLS

Similar articles