Abstract
Voltage is an important parameter that regulates the conductance of both intercellular and plasma membrane channels (undocked hemichannels) formed by the 21 members of the mammalian connexin gene family. Connexin channels display two forms of voltage-dependence, rectification of ionic currents and voltage-dependent gating. Ionic rectification results either from asymmetries in the distribution of fixed charges due to heterotypic pairing of different hemichannels, or by channel block, arising from differences in the concentrations of divalent cations on opposite sides of the junctional plaque. This rectification likely underpins the electrical rectification observed in some electrical synapses. Both intercellular and undocked hemichannels also display two distinct forms of voltage-dependent gating, termed Vj (fast)-gating and loop (slow)-gating. This review summarizes our current understanding of the molecular determinants and mechanisms underlying these conformational changes derived from experimental, molecular-genetic, structural, and computational approaches.
Connexins are tetraspan membrane proteins with intracellular N- and C-termini (Fig. 1) that in mammals are encoded by a 21 member gene family.1 Six connexin protein subunits assemble to form a hemichannel or connexon. In most cases, hemichannels are assemblages of six identical subunits, termed homomeric hemichannels. Heteromeric hemichannels comprised of different protein subunits can form in cells that express multiple connexin genes, if the assembly and trafficking cellular machinery allows their mixing. An intercellular channel is formed by the head to head docking of two hemichannels. These are termed homotypic channels, when the subunit composition of the docked hemichannels is identical, and heterotypic channels, when the subunit composition of the docked hemichannels is different. In principle, all combinations are possible (e.g., homomeric homotypic, homomeric heterotypic, heteromeric homotypic, etc.). However, not all homomeric hemichannels can pair to form intercellular channels. Pairing compatibility between any two given connexons has been mapped to the second extracellular domain (E2), although both extracellular loops are involved in intercellular channel formation.2
Intercellular channels aggregate to form gap junction plaques with characteristic morphology in EM micrographs (Fig. 1). Interestingly, gap junctions were first observed in invertebrates, however, these are encoded by the innexin gene family.3,4 Innexins share no substantial protein sequence homology with vertebrate connexins; however, they do share structural homology, which imparts functional similarity (both form large pore, voltage-gated intercellular ion channels). Innexins are not found in the chordate genome, nor are connexins found in the invertebrate genome, suggesting that the two families may have evolved from a common but distant ancestral protein. The pannexin gene family,5 which encodes membrane channels but not intercellular channels apparently, is found in both chordates and invertebrates and is a candidate ancestral gene. Despite lacking sequence homology, another gene family that encodes calcium homeostasis modulator (CALHM1) plasma membrane channels6 also shares structural homology to connexins, innexins, and pannexins. Interestingly, CALHM1 channels, like connexin channels, are gated by voltage and calcium ions and play an important role in regulating neuronal excitability in response to extracellular Ca2+.7
Connexins are unique among ion channel forming proteins in that they form both intercellular channels and channels that span the plasma membrane of single channels. These plasma membrane channels have been termed undocked or unapposed hemichannels. Intercellular channels play a vital physiological function in the heart and brain, where gap junctions form electrical synapses, and in non-excitable tissues, such as the liver and pancreas, where they couple groups of cells to synchronize cellular activity and secretion. Undocked hemichannels play an important role in paracrine signaling.8 The open probability of undocked hemichannels is low at the resting potentials of most cells and further reduced by the presence of extracellular Ca2+. Undocked hemichannels have the potential to regulate membrane potential (and hence excitability) in response to changes in calcium, as do CALMH channels.7 Reductions in extracellular calcium would increase hemichannel open probability, resulting in membrane depolarization that would move membrane potential closer to the threshold voltage required for firing action potentials. Notably, only a small fraction of intercellular channels appear to be active in a junctional plaque.9 The molecular bases for this property are unknown. Undocked hemichannels also may be organized into plaques, with only a small proportion of channels active; however, this possibility has not been examined to date.
For the most part, connexins form large pore ion channels (most with pore diameters of about 15 Å); remarkably, however, there is no strict correlation between single channel conductance, charge selectivity, and permeability to larger molecules.10 In general, connexin channels are permeable to ions, second messengers, (IP3, cAMP, and Ca2+),11 and large molecules (in some cases -1 kDa), probably including small regulatory RNA molecules;12 nevertheless, these properties differ according to the subunit composition of the channel.13 Single channel conductance of intercellular channels varies widely (from -5 to 300 pS), and charge selectivity ranges from slight anion selectivity to moderate cation selectivity.14,15 Notably, connexin channels do not discriminate among small metallic cations or anions. In most cases, the permeability ratios of metallic ions (e.g., PK/PNa) can be predicted from their mobility in bulk solution. This suggests that ions are fully hydrated when they traverse the connexin channel pore.
Connexins are expressed in virtually all organ systems and not surprisingly, mutations in connexin genes underlie several human diseases. At present, mutations in 10 connexin genes are known to underlie the etiology of least 15 human hereditary diseases.16,17 These include myelin related diseases, Charcot-Marie-Tooth (Cx32) and Pelizaeus-Merzbacher-Like disease (Cx47); both non-syndromic deafness and syndromic deafness associated with lethal skin disease, such as keratitis-ichthyosis-deafness syndrome (Cx26, Cx30, and Cx31); skin disease not associated with deafness, erythrokeratoderma (Cx30.3); cataract formation (Cx46 and Cx50); cardiovascular disease (Cx40 and 43); and oculodentodigital dysplasia (Cx43). Disease causing mutations can be grouped as loss of function or gain of function. A large category of loss of function mutations result from large shifts in voltage-dependence, resulting in channel closure at physiological conditions where connexin channels would normally be fully open.15,18
Membrane potential is an important parameter that regulates the conductance of both intercellular channels and undocked hemichannels. Strictly speaking, connexin channels display two forms of voltage dependence: 1) Instantaneous change in conductance that arises as a consequence of current rectification through single channels (i.e., the rate of ion permeation is a non-linear function of voltage). This is a property of the open channel and channel substates19,20 that occur without conformational changes. 2) Voltage-dependent changes in channel open probability that arise as a consequence of changes in protein conformation (i.e., allosteric transitions between open and closed states that are driven by voltage).
Although considerably less steep, the rectification of initial currents and single channel currents in symmetric salt, observed in the heterotypic Cx32/Cx26 junction (Fig. 2), qualitatively resembles that of a rectifying electrical synapse.21,22 Furshpan and Potter21 hypothesized that the junctional membrane behaved as an "electrical rectifier" or diode rather than a simple electrical resistor. The separation of fixed positive and negative charges across the junctional membrane would form a diode (p-n junction). P-n junctions can result in steeply rectifying current-voltage (I-V) relations, with steepness increasing markedly as greater amounts of positive and negative are segregated. Thus, they provide an attractive model for the molecular underpinning of steeply rectifying electrical synapses.
We19 examined the diode hypothesis by determining the molecular basis of electrical rectification displayed by Cx32/Cx26 heterotypic junctions. The results of the molecular-genetic studies supported the hypothesis by demonstrating that charged amino acid residues at the amino terminus and first extracellular loop are major determinants of the rectification of the heterotypic Cx32/Cx26 junction. The rectifying I-V relation of the heterotypic junction results from an asymmetry in the position and number of fixed charges present in the Cx32 and Cx26 hemichannels; indeed, the heterotypic channel forms a p-n junction with Cx26 side contributing the negative and Cx32 contributing the positive elements.
The significant concept arising from this study was that rectification of ionic currents requires some form of asymmetry. The asymmetry could be produced by differences in the distribution of fixed charges in the pore14,23,24 or by differential post-translational modification (e.g., phosphorylation or acetylation) of one element in a homotypic intercellular channel that forms the rectifying synaptic junction. Rectification of ionic current can also result from channel block, as exemplified by inwardly rectifying potassium channels, where outward currents are reduced by high-affinity channel block by endogenous polyamines and/or magnesium ions. In this case, the asymmetry reflects a difference in the concentrations of the blocking particles on opposite sides of the channel.
Recent studies have shown that most mammalian electrical synapses are formed by homotypic pairings of Cx36.25,26 While most mammalian electrical synapses do not rectify (i.e., they display linear current-voltage relations), the molecular basis for rectification, when observed, results from asymmetries in the concentrations of intracellular magnesium and ATP on the post and presynaptic sides of the synapse. Mg2+ and other divalent cations have been shown to interact with a charged residue, D47, located in the channel pore to block the channel,27,28 and this is likely to underlie rectification of some electrical synapses formed by Cx36. However, the electrical synapse found between auditory afferents and goldfish Mauthner cells is molecularly asymmetric (i.e., a heteromeric channel formed by docking Cx35 with Cx34.7),29 and this asymmetry may lead to rectification.
Voltage-dependent gating of ion channels is an allosteric process in which channels undergo structural changes in response to voltage to allow or prevent ion flux. Voltage (potential energy), does work on the molecule by changing the position (kinetic energy) of charged amino acids that in turn are coupled to the permeation barrier that blocks ionic flux when the channel resides in the closed state.
As intercellular channels span the plasma membrane of two adjacent cells, they can in principle be sensitive to two different electric fields: 1) that created by application of transjunctional voltage (Vj), which is defined as the difference in electric potential between the interior of two coupled cells, and 2) that created by the inside-outside voltage (termed Vi-o or Vm), which is defined as the difference in electric potential of the cytoplasm and the extracellular space (Fig. 3). In the case of undocked hemichannels, Vj is equivalent to changes in membrane potential in that a component of the electric field falls across the channel pore. These features of connexin voltage gating have been detailed by Bargiello and Brink.30
The conceptual framework underlying our understanding of voltage-dependent regulation of gap junction open probability is based on two papers from the Bennett lab,31,32 that described the equilibrium and kinetic properties of gap junction channels found in amphibian blastomeres. The major findings of their studies that are applicable to the majority of vertebrate connexins include the following:
1) Most vertebrate connexins are sensitive only to Vj; Cx26 gap junctions appear to be an exception to this generalization, as the initial conductance of these channels displays weak sensitivity to Vi-o,33 at least in macroscopic recordings of junctional currents. Interestingly, single channel current-voltage elicited by voltage ramps do not rectify.19 In contrast to vertebrate gap junctions, steady-state currents of Drosophila salivary gland gap junctions formed by innexin protein are markedly sensitive to both Vi-o and Vj.34
2) Voltage-gating is an intrinsic hemichannel property. Voltage sensors and gates are present in each hemichannel. Application of a given polarity of Vj favors closure of gates in one hemichannel and opening of gates in the apposed hemichannel. This is a consequence of the head to head docking and serial arrangement of the two hemichannels. This geometry also results in contingent gating, where closed gates in one hemichannel must open before gates can close in the apposed hemichannel when polarity of Vj is reversed.30,31
3) As the open probability of homotypic gap junction channels is maximal at Vj=0 and decreases with non-zero Vj, voltage must act to destabilize the open state and most likely stabilizes the closed state.
A major advance toward establishing the structure-function relations of voltage-gating in connexin channels was the discovery that connexin hemichannels could open in the plasma membrane of Xenopus oocytes,35 when unapposed by another hemichannel (undocked hemichannels). This property allowed direct observation of the operation of voltage gates and removed the complication of inferring the operation of serially arranged voltage-gates in intercellular channels.
Remarkably, single channel records of undocked Cx46 hemichannels displayed two distinct forms of voltage-gating, Vj- and loop-gating (also respectively known as fast- and slow-gating).36,37,38 Single channel records illustrating Vj- and loop-gating in the Cx32*43E1 hemichannel are shown in Fig. 4. Cx32*43E1 is a chimeric connexin that replaces the first extracellular loop (residues 41-70) of Cx32 with the corresponding Cx43 sequence. Hemichannels formed by the chimera express membrane currents in Xenopus laevis oocytes, when they are not docked to another hemichannel.39 The chimera provides a model system to study voltage-gating of Cx32 hemichannels.37
In single channel recordings, Vj-gating is characterized by transitions between the open and one or more sub-conductance states. These transitions cannot be resolved within the time resolution of the voltage clamp; hence the term fast-gating. In contrast, loop-gating is characterized by transitions between the open and a fully closed state; however, since this transition passes through a number of meta-stable intermediate conductance states, it has a measurable duration, and consequently, it appears to be a slow-gating event. The duration of the full transition is usually in the range of tens of milliseconds. The term loop-gating was coined by the Verselis lab that postulated that this gating resulted from conformational changes in extracellular loops.
The molecular determinants of Vj-gating appear to differ among connexins. Two different mechanisms have been proposed to account for channel entry into substates through fast transitions: 1) conformational changes resulting from movement of a voltage sensor located in the N-terminus, which is based on studies of Cx26 and Cx32,30,37,42,43,44 and 2) a particle-receptor mechanism (ball and chain model) where the carboxyl terminus (CT) acts as a gating particle by binding to a receptor located in the cytoplasmic loop (CL),45,46,47,48 which is based on studies of Cx43 and Cx40.
The role of the N-terminus in voltage gating arose from studies that sought to explain why the conductance-voltage relation of heterotypic Cx32/Cx26 junctions could not be predicted from the current-voltage relations of the corresponding homotypic channels (Fig. 2).33,49 We43 demonstrated that the asymmetry in the relaxation of steady-state junctional currents was a consequence of the opposite polarity of Vj-gating in hemichannels formed by the two connexins. Closure of the Cx26 hemichannel is favored when that side of the junction is relatively positive, whereas closure of the Cx32 hemichannel is favored when the Cx32 side of the junction is relatively negative. Thus, application of positive Vj to the Cx26 side of the junction favors closure of the Vj-gates in both hemichannels, while application of negative Vj to the Cx26 side favors opening of Vj-gates in both hemichannels.
Extensive analyses of gating polarity in a series of Cx26/Cx32 chimeras mapped the differences in gating polarity of Cx26 and Cx32 hemichannels to a difference in the charge of the second amino acid. Substitution of the negatively charged aspartic acid (D2) found in Cx26 for the neutral asparagine residue (N2) in Cx32 reversed the polarity of Vj-gating of Cx32 hemichannels from closure favored on relative negativity to closure favored on relative positivity. Substitution of neutral and positively charged residues at the second position in Cx32 conserved the negative gating polarity of Cx32 junctions, whereas substitution of the negatively charged aspartic acid with neutral or positively charged residues reversed the Vj-gating polarity of Cx26 hemichannel from closure favored at relatively positive potentials to closure favored at relatively negative potentials.
Interestingly, charge neutralization of D3 appears to reverse the polarity of Vj-gating in Cx46 and Cx50 hemichannels.50,51 The Cx50 study51 was based on the asymmetry of the conductance-voltage relation of the heterotypic junction Cx50/Cx50D3N, with closure observed for a single polarity of Vj. However, single channel recordings are needed to confirm the results, because it is known that Cx50 hemichannels display bi-polar fast gating events in single channel recordings.50
Single channel studies of negative charge and positive charge substitutions of the second residue in the Cx32*43E1 chimera confirmed that the polarity of Vj-gating was determined by the sign of the amino acid residing at the second position.42,44,52 Subsequent studies demonstrated that negative charge substitutions up to but not including the 12th residue could reverse the polarity of Vj-gating.42,52 These data were interpreted to indicate that the first 12 amino acids of the N-terminus reside in the channel pore, for only in this position would the domain be able to sense changes in just transjunctional voltage in intercellular channels. This conclusion was supported by structural determinations of Cx26 and Cx32 N-terminal peptides by NMR. These studies demonstrated the presence of a flexible open turn initiated by the 12th residue (glycine in both Cx26 and Cx32) that would allow the n-terminal half of the N-terminus to be positioned within the channel pore.53,54,55 Demonstration that cysteine substitutions of the 4th, 5th, and 8th position can be modified by a MTS reagents strongly support the proposed structure14 and Oh and Bargiello (unpublished observations). Significantly, the NMR derived structure agrees well with that of the N-terminus in the crystal structure of Cx26 gap junctions.56
The perfect electrostatic correlation between gating polarity and sign of charges in the N-terminus was interpreted to indicate that charges in the N-terminus formed at least part of the voltage-sensor for Vj-gating,43 although movement of the N-terminus in response to voltage has not been shown directly. Others56,57,58,59 have suggested that the N-terminus forms a gating particle to block the channel pore in Vj-gating, however, this possibility needs to be investigated further.37
Oh, et al.44 established that Vj-gating polarity reversal required only a negative charge at the second position in one of the six subunits of a connexin hemichannel. Interestingly, these heteromeric hemichannels displayed bi-polar Vj-gating (i.e., the channel open probability decreases at both inside positive and negative voltages and is maximal at 0 mV). Presumably, closure at inside positive potentials was initiated by movement of negatively charged subunits toward the cytoplasmic entrance to the channel pore, while closure at inside negative potentials was initiated by movement of positively charged subunits toward the cytoplasmic entrance. The data were interpreted to indicate that Vj-gating results from conformational changes in individual subunits rather than by a concerted movement of all six channel subunits. If gating were concerted (i.e., required the simultaneous repositioning of all six subunits), then closure of hemichannels containing negatively charged subunits in response to inside positive potentials would be opposed by the tendency of positively charged subunits to move in the opposite direction and immediately open. Hence, one would expect that the residency in a closed state in these heteromeric hemichannels would be exceedingly brief; the channels would flicker rapidly between open and closed states with both membrane depolarization and hyperpolarization. This was not observed.
Remarkably, several 43E1 homomeric hemichannels containing charge substitutions in the N-terminus also display bi-polar Vj-gating. These include, T8D, N2E+G5K, and N2R+G5D. While the mechanism underlying the basis of bi-polar channels has not been established, it can be explained by modeling the Vj-voltage sensor as a center open toggle switch.42 In this scenario channel closure would initiated by either the inward or outward movement of the voltage sensor, such that the voltage sensor crosses one energy barrier for one voltage polarity and the other barrier for the opposite polarity. Interestingly, the charges at the second position appear to have a larger role in determining gating polarity, as voltage sensitivity of bipolar channels correlates with the sign of the charge at this position. However, this class of model cannot adequately explain the bipolarity of heteromeric channels, whose explanation tacitly assumes that the direction of movement of the voltage sensor is identical for all mutations (always toward the cytoplasm). Resolution of the role of the N-terminus requires direct observation of movement of the N-terminus in response to voltage. In other ion channels, fluorescence quenching, luminescence resonance energy transfer, and fluorescence resonance energy transfer have been used to demonstrate voltage sensor movements.60,61 While feasible, application of these methods to undocked connexin hemichannels is technically challenging, as hemichannels appear to aggregate into well dispersed plaques. Furthermore, the results may prove difficult to interpret because only a small fraction of connexin channels contained in plaques appear to be active.9 Thus, signals reporting movements would probably be very small.
Finally, it is important to understand that the gating model tacitly assumes that the difference in gating polarity of Cx26 and Cx32 hemichannels reflects the oppositely charged voltage sensors, negative in Cx26 and positive in Cx32. Originally, we43 suggested that the positive charge was contributed by the N-terminal methionine residue. However, characterization of the N-termini of Cx2662 and Cx32 (Bargiello, unpublished) by tandem mass spectroscopy have demonstrated that the positive charge of the N-terminal methionine residue is neutralized by acetylation. It is conceivable, that not all methionine residues are acetylated, thus at least one subunit carries a positive charge. Alternatively, it is possible that positive charge results from the dipole associated with the α-helical N-terminus, or that that residues carry partial positive charges. For example, in the Chemistry at HARvard Macromolecular Mechanics (CHARMM) topology file, atoms HD21 and HD22 in the asparagine side chain together carry a positive charge (0.62) that is balanced by the negative charge of atom ND2 (-0.62). We also cannot rule out the possibility that the N-terminus does not contain the voltage sensor and that charge substitutions in this domain alter the electrostatic profile of the channel and reverse the direction of the voltage drop across conserved pore lining charges that form the voltage sensor. Knowledge of the structure of the Vj-closed state would be of great value in clarifying the gating mechanism and the role of the N-terminus.
The ball and chain model (also termed the particle-receptor model) was originally proposed to explain pH gating of Cx43 channels by Delmar and co-workers.63 The model proposes that changes in pH cause a conformational change in the CL of connexin channels that exposes a receptor domain (L2 region) to which binding of a region of the CT either closes or stabilizes the closed state. The model was later extended to provide a mechanism to explain Vj (fast)-voltage-dependent gating, following demonstration that deletions of the CT of Cx43 and Cx40, or addition of green fluorescent protein to the C-terminus appear to abolish Vj-gating.40,45,46
Revilla, et al.48 concluded that the CT of Cx32, like that of Cx43, was critical to the expression of Vj-gating following truncation of the Cx32 CT to residue 220. However, this was based on their interpretation of kinetic data, which equated a fast component in current relaxations observed in macroscopic recordings of Cx32 intercellular channels to Vj-gating. Loss of Vj gates and persistence loop (slow) gates were not confirmed by single-channel recordings. Recently, Kwon, et al.,64 demonstrated that both Vj and loop gates are operational in a truncation mutation that removes all but the first four CT residues (ACAR219) of the Cx32*43E1 hemichannel. Thus, it does not appear that the CT is required for expression of Vj-gating in Cx32.
Given the difference in molecular determinants reported for Cx32, Cx26, Cx43, and Cx40 hemichannels, the fundamental questions become whether there a mechanistic relation between the role of the NT and that of the CL-CT interaction in Vj-gating and whether fast-gating arises by the same mechanism in different connexin channels. One possibility, consistent with the view that three domains participate in the same process, is that voltage acts upon charges in the NT to induce conformational changes that include exposure of the L2 receptor in the CL, and that this conformation is stabilized by low-affinity binding of specific sequence contained in the CT. If this mechanism is shared by all connexin hemichannels, then the operation of the Vj (fast)-gate in the CT truncations of Cx32*43E1 can be explained if the four remaining CT residues (ACAR219) are sufficient to interact with a region of the CL near the TM3 border to stabilize the closed conformation. Alternatively, it is possible that the conformation of the Cx32 Vj-closed state is stable in the absence of interactions with the CT, and thus, the CT would not be required for Cx26 and Cx32, but may be required to stabilize the closed state of Cx43 and Cx40 hemichannels.
Voltage-dependent loop-gating is the mechanism that in conjunction with divalent cations reduces the open probability of undocked hemichannels in the plasma membrane. It has been proposed that the voltage dependent-loop gate is the same as the one closed by chemical gating agents such acidification and extracellular Ca2+,38 however this is not established and is currently being investigated by both structural and experimental approaches.
In all connexins examined to date, loop-gate closure in undocked hemichannels is favored at inside negative potentials (membrane hyperpolarization). In intercellular channels, loop gate closure is favored on the relatively negative side of the junction. Unlike, Vj-gating, there are no known mutations or combinations of mutations that reverse loop-gating polarity. In many intercellular channels, the voltage sensitivity of loop gates is less than that of Vj-gates, such that over intermediate ranges of transjunctional voltages, the plateau observed in conductance-voltage relations of steady-state currents (e.g., Cx32 homotypic junctions) (Fig. 2), is due to entry of a hemichannel into a Vj-substate, and there is little if any closure of loop-gates at these potentials. At larger VjVjs, the conductance-voltage relations can decrease to 0 as a consequence of loop-gate closure (see for example, the conductance-voltage relation of Cx32*KE intercellular channels in43).
Physiologic concentrations of Ca2+ and Mg2+ have been shown to stabilize the loop-gate closed state of Cx46 hemichannels65 and endogenous Xenopus Cx38 hemichannels (see Supplemental information in66). Ca2+ has also been reported to gate connexin channels without application of voltage. This may result by destabilization of the open state as reported by Contreras and co-workers67,68 for Cx26 hemichannels. Barrio and colleagues showed that mutations of Asp169 and Asp178 at the extracellular vestibule significantly reduce the ability of extracellular Ca2+ to close Cx32 hemichannels;69 however, it is unclear whether this is due to changes in interaction(s) that are involved in stabilizing voltage-dependent loop-gates. Atomic force microscopy studies of connexin hemichannels have indicated a narrowing of extracellular channel entrance with 2 mM Ca2+ (but not Mg2+) for Cx2670 in the absence of membrane voltage. Divalent cations have been shown to block Cx36 hemichannels by interactions with the conserved pore lining residue D47.27 Based on the apparent multiplicity in reported actions of extracellular Ca2+, it is likely that there are multiple mechanisms underlying Ca2+ regulation of connexin hemichannels and that different connexin channels may have multiple regulatory binding sites.71 The stabilization of loop-gates is likely to be just one of several different mechanisms.
The distinctive feature of loop-gating is the slow time constant of the full gating transition from fully open to fully closed states (tens of milliseconds) (Fig. 4). The time course is explained by passage through a series of meta-stable states with occupancy in the fully closed state strongly favored at large negative potentials. A macroscopic recording of Cx32*43E1 N2E ΔCT hemichannels expressed in Xenopus oocytes is shown in Fig. 5. Current relaxations at inside positive potentials (red traces) correspond to closure of Vj-gates, while those at inside negative potentials result from loop-gate closure. For Cx32*43E1 N2E ΔCT the gating charge for loop-gating calculated from limiting slope shown in Fig. 5B is -0.5. The gating charge of Cx46 hemichannels is -2.2 (limiting slope from Popen data of65). The difference in gating charge could mean that more charge moves through the same electric field in Cx46, or that the electric field differs in the two hemichannels, or both. Knowledge of open and closed structures allows these alternatives to be distinguished.
For Cx32*43E1 N2E ΔCT, the macroscopic current relaxation at -70 mV is well fitted by two exponentials with time constants -6.46 and 0.83 seconds (0 Mg2+), 4.19 and 0.55 (1.8 mM Mg2+), and 4.07 and 0.52 (5 mM Mg2+). Progressive time constant lengthening as a function of (Mg2+) is consistent with closed state stabilization. The time constants of Cx46 are shorter, -1.2 and 0.23 seconds at -70 mV in 1.8 Mg2+. The time constant of Cx26 is longer, exceeding 10 seconds at -70 mV in 1.8 Mg2+. The longer of each pair of time constants most likely corresponds to full channel closures and the shorter time constants to partial closures ("failed transitions").
According to classical transition state theory (TST), the longer time constant suggests that the energy barrier separating fully open and fully closed states is in the range of 15-17 kcal/mol. Remarkably, undocked Cx46 single channel records from the Verselis lab show loop-gating transitions in response to small membrane depolarizations, as well as membrane hyperpolarization.36 This indicates that transition between open and closed states can take place in the absence of voltage [i.e., with thermal energy alone (-0.62 kcal/mol at 310 K)], despite the extremely high energy barrier predicted by TST. This suggests that approaches based on TST, which relate rate constants exclusively to the heights of energy barriers, may not provide a suitable conceptual framework to elucidate the mechanisms of conformational change of loop-gating. An alternate conceptual framework is provided by transition path theory (TPT).72,73 TPT is founded in statistical mechanics and considers the transition-path ensemble in terms of the free energy landscape of different conformational states. It takes into account the likelihood that only a subset of the transient conformational fluctuations of open or closed states has access to paths that lead to successful transitions. TPT interprets rate constants of conformational transitions to reflect not only barrier heights but also the complexity and "ruggedness" of the free energy landscapes. The simplest analogy is to picture a maze: as the complexity of the maze increases, the average time taken to successfully transit the maze increases.
Our current understanding of the molecular mechanism underlying loop-gating derives from three sources: 1) experimental studies that defined the structure of the loop-gate closed state;66,74,75 2) the atomic structure of the Cx26 channel (PDB:2ZW3)56 and its refinement by all atom Molecular Dynamics (MD) simulation and validation by Grand Canonical Monte Carlo Brownian Dynamics simulation (GCMD/BD);23 3) identification and computational analyses of van der Waals and electrostatic interactions that stabilize the permeability barrier in the open state.
Solution of the atomic structure of a native ion channel in a voltage-gated closed state is a challenge common to all voltage-gated channels. One cannot impose a stable, defined voltage gradient to an isolated channel that is currently compatible with structural determination by NMR, electron paramagnetic resonance, or X-ray crystallography. A powerful alternative method is to use biochemical/functional assays to define the distance between substituted cysteine residues along the length of the channel pore. Methods such as state dependent formation of Cd2+-thiolate metal bridges, bi-functional chemical cross-linkers, and disulfide bonds serve as "molecular rulers" that define the distance between substituted cysteines when the channel resides in a conformation of interest. The experimental rationale and interpretation of results of Cd2+-thiolate metal bridge formation in determining conformational changes has been discussed previously.37,66,76 The fundamental idea is to trap or "lock" the channel in a given conformation by formation of metal bridges.
Fig. 6 summarizes the results of metal-bridge formation following investigation of cysteine substitutions at 25 loci that span the length of the Cx32*43E1 channel pore. The largest conformational changes are in the most stable region of the channel pore, the 310 or parahelix, formed by amino acids 41-50, where pore diameter is reduced from 15 to 20 Å to less than 4 Å. This reduction in pore diameter is sufficient to form a permeability barrier, given that the diameter of hydrated K+ and Cl- ions is 6.62 Å and 6.64 Å, respectively.77 The data, in conjunction with the atomic structure models of Cx2623,56 and Cx32*43E1 channels,64 show a marked reorganization of the parahelix, with A43C moving into the channel pore with loop-gate closure. Similarly, A40C only coordinates Cd2+ in the loop-gate closed state, a feature which requires straightening of the TM1/E1 bend angle. Straightening of this angle predicts that the intracellular channel formed by residues at the border of TM2 and CL and NT will move closer together. This prediction was confirmed by formation of metal bridges at E109C and L108C66 and at 3 residues in the N-terminus (Kwon, Oh, Bargiello, Dowd, and Bargiello, submitted). The diameter of the channel pore at the intracellular entrance would be reduced to about 10 Å. The extracellular entrance, defined by residue Q56, does not appear to undergo large conformational changes with voltage-gating. We interpret these results to indicate that the loop-gate permeability is essentially focal; in that, conformational changes in the parahelix, but not the channel entrances, are sufficient to prevent ion flux.
Surprisingly, the largest conformational change in loop-gating occurs in the most stable region of the Cx26 hemichannel pore,78 the parahelix formed by amino acids 42-51 in Cx26. As voltage effects channel closure by destabilization of the open state, elucidation of the atomic interactions that stabilize the permeability barrier formed by the parahelix should provide insights into the mechanism of loop-gating at the atomic level.
The picture of loop-gating that emerges from MD simulations23,78 is that an electrostatic network (emanating from the parahelix) that interconnects all six subunits forms the nucleus of the loop-gate voltage sensor. In Cx26, this includes residues E42, D46, E47, R75, R184, E187, and K188. This charge ring meets the requirement that a connexin voltage sensor must reside in the channel pore where it can sense transjunctional voltage in both open and closed conformation. The MD simulations show how reorganization of the electrostatic network could be directly coupled to the structure of the permeability barrier formed by reorganization of the parahelix and straightening of the TM1/E1 bend angle.78
The intersubunit connection provided by the electrostatic network suggests a high degree of positive cooperativity, such that changes in conformation in any given subunit will be transmitted to the two adjacent subunits. This suggests that loop-gating most likely arises from the simultaneous movement of all six subunits (i.e., a concerted gating mechanism). We favor a mechanism in which the intermediate states observed in single channel records correspond to the linked electrostatic networks stepping together through a series of intermediate structures, each of which increases pore occlusion.
Finally, Kwon, et al.66 also described an extensive intrasubunit van der Waals network that stabilizes both the parahelix and TM1/E1 bend and modulates the dynamics of electrostatic interactions among residues that are believed to form the loop-gate voltage sensor. We proposed that because the open state is stabilized by an additive effect of multiple weak vdW and electrostatic interactions, the transition to the closed state most likely proceeds by the sequential destabilization of open-state interactions and formation of new interactions that stabilize the intermediate and fully closed states. This provides a mechanism to surmount the large energy barrier predicted by TST and one that is compatible with application of TPT.
Our current understanding of voltage regulation of connexin channels is derived from a combination of experimental, molecular-genetic, structural and computational approaches. Overall, the elucidation of structure-function relations has been greatly advanced by solution of the atomic structure of Cx26 by X-ray crystallography by Maeda and co-workers56 and its refinement by all atom MD simulation.23,79,80 Yeager and co-workers have also solved the structure of Cx26 by X-ray crystallography using different conditions, including crystallization in the presence of Ca2+,81 however, this study has not yet been published. We anticipate that the solution of atomic structure of other connexin channels will be forthcoming and that this will provide additional information to guide our understanding of connexin structure-function.
A major advantage of ion channel research has been the development of computational methods that allow determination of functional properties of atomic structures. These are exemplified by, but not restricted to, determination of ion permeation through large pore ion channels by application of GCMC/BD,82,83,84,85 calculation of gating charge,86 and calculation of free energy differences (ΔΔG) arising from mutation by FEP/MD.87 These methods provide a powerful mean to test the validity of atomic structure by comparison of computed and experimental measurements. It should be pointed out that all methods, structural, experimental, and computational, are subject to intrinsic assumptions and consequently may have errors. The best way to overcome this limitation is to apply diverse methods in parallel to arrive at consensus structures and mechanisms.88 In this review, we summarize our efforts to apply this strategy to study the regulation of connexin channel conductance by voltage.
The next critical step in our understanding of voltage-gating is obtaining atomic resolution models of voltage-gated closed states. Ultimately, validated models of open and closed states will allow the application of computational methods that define the transition pathway connecting states and, thereby, to determine how states are coupled by voltage. This information will undoubtedly prove valuable in our attempts to devise treatment strategies for connexin diseases, as many of these are caused by mutations that alter voltage gating of intercellular and undocked connexin channels.
Figures and Tables
 | Fig. 1Membrane topology of connexin subunits and channel composition. A connexin subunit is composed of four transmembrane domains (TM1, TM2, TM3, and TM4), two extracellular loops (E1 and E2), amino and carboxyl termini (NT and CT, respectively), and a cytoplasmic loop (CL). Six connexin subunits assemble to form a hemichannel or connexon, which is termed homomeric if all subunits are identical and heteromeric if comprised of different connexin subunits. Head to head docking of two connexons forms an intercellular channel, aggregates of which are termed gap junctions and visible as plaques in freeze fracture and transmission electron microscopy. Homotypic intercellular channels are formed by docking two hemichannels of identical subunit composition, be it homomeric or heteromeric. Heterotypic intercellular channels are formed by docking hemichannels that differ in subunit composition. |
 | Fig. 2Representative current traces and conductance-voltage plots of initial and steady state junctional currents obtained from pairs of Xenopus oocytes. (A) Cx32 homotypic channels. (B) Cx26 homotypic channels. (C) Cx32/Cx26 heterotypic channels. Initial conductance (▾) and steady-state conductance (▿) are plotted as the function of the applied Vj relative to the cytoplasm of the right-side hemichannel. Taken with permission from Oh, et al. J Gen Physiol 1999;114:339-64.19 |
 | Fig. 3Diagram of a gap-junction channel showing presumed isopotential lines resulting from the application of Vi-o (A) and Vj (B). Vi-o was established by simultaneously holding the membrane potential of both cells at -50 mV. Vj does not exist in this case. Vj was established by voltage clamping the left cell to a holding potential of -100 mV, while the right cell was voltage clamped to 0 mV. Note that the generation of Vj also generates Vi-o in regions of the channel, but Vi-o varies with the voltage paradigm. Holding the left cell at -50 mV and the right cell at +50 mV generates the same Vj as the previous example (i.e., the voltage difference across the channel is -100 mV relative to the left cell). Note that Vi-o would differ in this case, because the absolute membrane potentials used to generate Vj differ in the two cases. Taken with permission from Bargiello and Brink.30 |
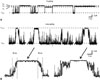 | Fig. 4Single channel records of an undocked Cx32*Cx43E1 hemichannel expressed in a Xenopus oocyte. (A) Outside-out record of a single channel illustrating closures by Vj-gating to three substates at a holding potential of -100 mV. (B) Cell-attached recording of a single wild-type channel illustrating six loop-gating events at a holding potential of -70 mV. Note the slow time course of the transitions and that not all transitions necessarily lead to full channel closure. Taken with permission from Bargiello, et al. Biochim Biophys Acta 2012;1818:1807-22.37 |
 | Fig. 5(A) Representative macroscopic recording of Cx32*43E1 N2E 219 stop hemichannels in Xenopus oocytes in bath solution containing 100 mM cesium methanesulfonate, 10 mM Hepes, pH 7.6, elicited by voltage steps from 50 to -120 mV in 10 mV increments from a holding potential of 0 mV. Current traces depicted in red correspond to current relaxations corresponding to Vj-gating; black current traces to loop-gating. (B) Semilogarithmic plot of open probability at steady state and membrane potential (n=6 oocytes). The limiting slope is drawn from which gating charge is estimated to be -0.5. |
 | Fig. 6Schematic illustration of open and closed state models of Cx32*43E1 hemichannels cysteine substitutions of residues shown in the open state model are accessible to membrane impermeant thiol modifying reagents. Cysteine substitutions of residues shown in the closed state, with the exception of 56 (red), form Cd2+-thiol metal bridges when the channel resides in the loop-gate closed state. Residues 40 and 43 (green) do not line the open channel pore but enter the pore in the loop-gate closed state. A43C hemichannels form disulfide bridges in western blots. The approximate boundaries of the membrane are shown by dotted lines. This figure was updated to include unpublished data with permission. Previous versions of the figure appeared in Biochim Biophys Acta (BBA)-Biomembranes37 and J Gen Physiol.66 |
ACKNOWLEDGEMENTS
We thank our many colleagues and collaborators for insights they have provided into our past and ongoing investigation of the structure-function relations of connexin channels, especially Drs. Taekyung Kwon, Qingxiu Tang, Terry Dowd, Andrew Harris, and Benoît Roux. We apologize for any omissions. Our studies have been supported by grants from the National Institutes of Health (US) GM 046889 and GM 098584. Additional support from the Albert Einstein College of Medicine is gratefully acknowledged.
References
1. Beyer EC, Berthoud VM. The Family of Connexin Genes. In : Harris AL, Locke D, editors. Connexins: a guide. New York, NY: Humana Press;2009. p. 3–26.
2. Bai D, Wang AH. Extracellular domains play different roles in gap junction formation and docking compatibility. Biochem J. 2014; 458:1–10.

4. Bauer R, Löer B, Ostrowski K, Martini J, Weimbs A, Lechner H, et al. Intercellular communication: the Drosophila innexin multiprotein family of gap junction proteins. Chem Biol. 2005; 12:515–526.

5. Penuela S, Gehi R, Laird DW. The biochemistry and function of pannexin channels. Biochim Biophys Acta. 2013; 1828:15–22.

6. Siebert AP, Ma Z, Grevet JD, Demuro A, Parker I, Foskett JK. Structural and functional similarities of calcium homeostasis modulator 1 (CALHM1) ion channel with connexins, pannexins, and innexins. J Biol Chem. 2013; 288:6140–6153.

7. Ma Z, Siebert AP, Cheung KH, Lee RJ, Johnson B, Cohen AS, et al. Calcium homeostasis modulator 1 (CALHM1) is the pore-forming subunit of an ion channel that mediates extracellular Ca2+ regulation of neuronal excitability. Proc Natl Acad Sci U S A. 2012; 109:E1963–E1971.
8. Wang N, De Bock M, Decrock E, Bol M, Gadicherla A, Vinken M, et al. Paracrine signaling through plasma membrane hemichannels. Biochim Biophys Acta. 2013; 1828:35–50.

9. Bukauskas FF, Jordan K, Bukauskiene A, Bennett MV, Lampe PD, Laird DW, et al. Clustering of connexin 43-enhanced green fluorescent protein gap junction channels and functional coupling in living cells. Proc Natl Acad Sci U S A. 2000; 97:2556–2561.

10. Harris AL, Locke D. Permeability of connexin channels. In : Harris AL, Locke D, editors. Connexins: a guide. New York, NY: Humana Press;2009. p. 576.
11. Kanaporis G, Mese G, Valiuniene L, White TW, Brink PR, Valiunas V. Gap junction channels exhibit connexin-specific permeability to cyclic nucleotides. J Gen Physiol. 2008; 131:293–305.

12. Valiunas V, Polosina YY, Miller H, Potapova IA, Valiuniene L, Doronin S, et al. Connexin-specific cell-to-cell transfer of short interfering RNA by gap junctions. J Physiol. 2005; 568(Pt 2):459–468.

13. Elfgang C, Eckert R, Lichtenberg-Fraté H, Butterweck A, Traub O, Klein RA, et al. Specific permeability and selective formation of gap junction channels in connexin-transfected HeLa cells. J Cell Biol. 1995; 129:805–817.

14. Oh S, Verselis VK, Bargiello TA. Charges dispersed over the permeation pathway determine the charge selectivity and conductance of a Cx32 chimeric hemichannel. J Physiol. 2008; 586:2445–2461.

15. Oh S, Ri Y, Bennett MV, Trexler EB, Verselis VK, Bargiello TA. Changes in permeability caused by connexin 32 mutations underlie X-linked Charcot-Marie-Tooth disease. Neuron. 1997; 19:927–938.

16. Pfenniger A, Wohlwend A, Kwak BR. Mutations in connexin genes and disease. Eur J Clin Invest. 2011; 41:103–116.

17. Abrams CK, Freidin M. GJB1-associated X-linked Charcot-Marie-Tooth disease, a disorder affecting the central and peripheral nervous systems. Cell Tissue Res. 2014; [Epub ahead of print].

18. Abrams CK, Islam M, Mahmoud R, Kwon T, Bargiello TA, Freidin MM. Functional requirement for a highly conserved charged residue at position 75 in the gap junction protein connexin 32. J Biol Chem. 2013; 288:3609–3619.

19. Oh S, Rubin JB, Bennett MV, Verselis VK, Bargiello TA. Molecular determinants of electrical rectification of single channel conductance in gap junctions formed by connexins 26 and 32. J Gen Physiol. 1999; 114:339–364.

20. Bukauskas FF, Bukauskiene A, Verselis VK. Conductance and permeability of the residual state of connexin43 gap junction channels. J Gen Physiol. 2002; 119:171–185.

21. Furshpan EJ, Potter DD. Transmission at the giant motor synapses of the crayfish. J Physiol. 1959; 145:289–325.

22. Auerbach AA, Bennett MV. A rectifying electrotonic synapse in the central nervous system of a vertebrate. J Gen Physiol. 1969; 53:211–237.

23. Kwon T, Harris AL, Rossi A, Bargiello TA. Molecular dynamics simulations of the Cx26 hemichannel: evaluation of structural models with Brownian dynamics. J Gen Physiol. 2011; 138:475–493.

24. Trexler EB, Bukauskas FF, Kronengold J, Bargiello TA, Verselis VK. The first extracellular loop domain is a major determinant of charge selectivity in connexin46 channels. Biophys J. 2000; 79:3036–3051.

25. Hamzei-Sichani F, Davidson KG, Yasumura T, Janssen WG, Wearne SL, Hof PR, et al. Mixed Electrical-Chemical Synapses in Adult Rat Hippocampus are Primarily Glutamatergic and Coupled by Connexin-36. Front Neuroanat. 2012; 6:13.

26. Bautista W, Rash JE, Vanderpool KG, Yasumura T, Nagy JI. Re-evaluation of connexins associated with motoneurons in rodent spinal cord, sexually dimorphic motor nuclei and trigeminal motor nucleus. Eur J Neurosci. 2014; 39:757–770.

27. Palacios-Prado N, Chapuis S, Panjkovich A, Fregeac J, Nagy JI, Bukauskas FF. Molecular determinants of magnesium-dependent synaptic plasticity at electrical synapses formed by connexin36. Nat Commun. 2014; 5:4667.

28. Palacios-Prado N, Hoge G, Marandykina A, Rimkute L, Chapuis S, Paulauskas N, et al. Intracellular magnesium-dependent modulation of gap junction channels formed by neuronal connexin36. J Neurosci. 2013; 33:4741–4753.

29. Rash JE, Curti S, Vanderpool KG, Kamasawa N, Nannapaneni S, Palacios-Prado N, et al. Molecular and functional asymmetry at a vertebrate electrical synapse. Neuron. 2013; 79:957–969.

30. Bargiello T, Brink P. Voltage-Gating Mechanisms of Connexin Channels. In : Harris AL, Locke D, editors. Connexins: a guide. New York, NY: Humana Press;2009. p. 103–128.
31. Harris AL, Spray DC, Bennett MV. Kinetic properties of a voltage-dependent junctional conductance. J Gen Physiol. 1981; 77:95–117.

32. Spray DC, Harris AL, Bennett MV. Equilibrium properties of a voltage-dependent junctional conductance. J Gen Physiol. 1981; 77:77–93.

33. Barrio LC, Suchyna T, Bargiello T, Xu LX, Roginski RS, Bennett MV, et al. Gap junctions formed by connexins 26 and 32 alone and in combination are differently affected by applied voltage. Proc Natl Acad Sci U S A. 1991; 88:8410–8414.

34. Verselis VK, Bennett MV, Bargiello TA. A voltage-dependent gap junction in Drosophila melanogaster. Biophys J. 1991; 59:114–126.

35. Paul DL, Ebihara L, Takemoto LJ, Swenson KI, Goodenough DA. Connexin46, a novel lens gap junction protein, induces voltage-gated currents in nonjunctional plasma membrane of Xenopus oocytes. J Cell Biol. 1991; 115:1077–1089.

36. Trexler EB, Bennett MV, Bargiello TA, Verselis VK. Voltage gating and permeation in a gap junction hemichannel. Proc Natl Acad Sci U S A. 1996; 93:5836–5841.

37. Bargiello TA, Tang Q, Oh S, Kwon T. Voltage-dependent conformational changes in connexin channels. Biochim Biophys Acta. 2012; 1818:1807–1822.

39. Pfahnl A, Zhou XW, Werner R, Dahl G. A chimeric connexin forming gap junction hemichannels. Pflugers Arch. 1997; 433:773–779.

40. Bukauskas FF, Angele AB, Verselis VK, Bennett MV. Coupling asymmetry of heterotypic connexin 45/ connexin 43-EGFP gap junctions: properties of fast and slow gating mechanisms. Proc Natl Acad Sci U S A. 2002; 99:7113–7118.

41. Contreras JE, Sáez JC, Bukauskas FF, Bennett MV. Gating and regulation of connexin 43 (Cx43) hemichannels. Proc Natl Acad Sci U S A. 2003; 100:11388–11393.

42. Oh S, Rivkin S, Tang Q, Verselis VK, Bargiello TA. Determinants of gating polarity of a connexin 32 hemichannel. Biophys J. 2004; 87:912–928.

43. Verselis VK, Ginter CS, Bargiello TA. Opposite voltage gating polarities of two closely related connexins. Nature. 1994; 368:348–351.

44. Oh S, Abrams CK, Verselis VK, Bargiello TA. Stoichiometry of transjunctional voltage-gating polarity reversal by a negative charge substitution in the amino terminus of a connexin32 chimera. J Gen Physiol. 2000; 116:13–31.

45. Anumonwo JM, Taffet SM, Gu H, Chanson M, Moreno AP, Delmar M. The carboxyl terminal domain regulates the unitary conductance and voltage dependence of connexin40 gap junction channels. Circ Res. 2001; 88:666–673.

46. Moreno AP, Chanson M, Elenes S, Anumonwo J, Scerri I, Gu H, et al. Role of the carboxyl terminal of connexin43 in transjunctional fast voltage gating. Circ Res. 2002; 90:450–457.

47. Shibayama J, Gutiérrez C, González D, Kieken F, Seki A, Carrión JR, et al. Effect of charge substitutions at residue his-142 on voltage gating of connexin43 channels. Biophys J. 2006; 91:4054–4063.

48. Revilla A, Castro C, Barrio LC. Molecular dissection of transjunctional voltage dependence in the connexin-32 and connexin-43 junctions. Biophys J. 1999; 77:1374–1383.

49. Rubin JB, Verselis VK, Bennett MV, Bargiello TA. Molecular analysis of voltage dependence of heterotypic gap junctions formed by connexins 26 and 32. Biophys J. 1992; 62:183–193.

50. Srinivas M, Kronengold J, Bukauskas FF, Bargiello TA, Verselis VK. Correlative studies of gating in Cx46 and Cx50 hemichannels and gap junction channels. Biophys J. 2005; 88:1725–1739.

51. Peracchia C, Peracchia LL. Inversion of both gating polarity and CO2 sensitivity of voltage gating with D3N mutation of Cx50. Am J Physiol Cell Physiol. 2005; 288:C1381–C1389.
52. Purnick PE, Oh S, Abrams CK, Verselis VK, Bargiello TA. Reversal of the gating polarity of gap junctions by negative charge substitutions in the N-terminus of connexin 32. Biophys J. 2000; 79:2403–2415.

53. Purnick PE, Benjamin DC, Verselis VK, Bargiello TA, Dowd TL. Structure of the amino terminus of a gap junction protein. Arch Biochem Biophys. 2000; 381:181–190.

54. Kalmatsky BD, Bhagan S, Tang Q, Bargiello TA, Dowd TL. Structural studies of the N-terminus of Connexin 32 using 1H NMR spectroscopy. Arch Biochem Biophys. 2009; 490:9–16.

55. Kalmatsky BD, Batir Y, Bargiello TA, Dowd TL. Structural studies of N-terminal mutants of connexin 32 using (1)H NMR spectroscopy. Arch Biochem Biophys. 2012; 526:1–8.

56. Maeda S, Nakagawa S, Suga M, Yamashita E, Oshima A, Fujiyoshi Y, et al. Structure of the connexin 26 gap junction channel at 3.5 A resolution. Nature. 2009; 458:597–602.

57. Oshima A, Tani K, Hiroaki Y, Fujiyoshi Y, Sosinsky GE. Three-dimensional structure of a human connexin26 gap junction channel reveals a plug in the vestibule. Proc Natl Acad Sci U S A. 2007; 104:10034–10039.

58. Oshima A, Tani K, Hiroaki Y, Fujiyoshi Y, Sosinsky GE. Projection structure of a N-terminal deletion mutant of connexin 26 channel with decreased central pore density. Cell Commun Adhes. 2008; 15:85–93.

59. Oshima A, Tani K, Toloue MM, Hiroaki Y, Smock A, Inukai S, et al. Asymmetric configurations and N-terminal rearrangements in connexin26 gap junction channels. J Mol Biol. 2011; 405:724–735.

60. Cha A, Snyder GE, Selvin PR, Bezanilla F. Atomic scale movement of the voltage-sensing region in a potassium channel measured via spectroscopy. Nature. 1999; 402:809–813.

61. Bezanilla F. The voltage sensor in voltage-dependent ion channels. Physiol Rev. 2000; 80:555–592.

62. Locke D, Bian S, Li H, Harris AL. Post-translational modifications of connexin26 revealed by mass spectrometry. Biochem J. 2009; 424:385–398.

63. Ek-Vitorín JF, Calero G, Morley GE, Coombs W, Taffet SM, Delmar M. PH regulation of connexin43: molecular analysis of the gating particle. Biophys J. 1996; 71:1273–1284.

64. Kwon T, Dowd TL, Bargiello TA. The carboxyl terminal residues 220-283 are not required for voltage gating of a chimeric connexin32 hemichannel. Biophys J. 2013; 105:1376–1382.

65. Verselis VK, Srinivas M. Divalent cations regulate connexin hemichannels by modulating intrinsic voltage-dependent gating. J Gen Physiol. 2008; 132:315–327.

66. Kwon T, Tang Q, Bargiello TA. Voltage-dependent gating of the Cx32*43E1 hemichannel: conformational changes at the channel entrances. J Gen Physiol. 2013; 141:243–259.

67. Lopez W, Gonzalez J, Liu Y, Harris AL, Contreras JE. Insights on the mechanisms of Ca(2+) regulation of connexin26 hemichannels revealed by human pathogenic mutations (D50N/Y). J Gen Physiol. 2013; 142:23–35.

68. Lopez W, Liu Y, Harris AL, Contreras JE. Divalent regulation and intersubunit interactions of human connexin26 (Cx26) hemichannels. Channels (Austin). 2014; 8:1–4.

69. Gómez-Hernández JM, de Miguel M, Larrosa B, González D, Barrio LC. Molecular basis of calcium regulation in connexin-32 hemichannels. Proc Natl Acad Sci U S A. 2003; 100:16030–16035.

70. Müller DJ, Hand GM, Engel A, Sosinsky GE. Conformational changes in surface structures of isolated connexin 26 gap junctions. EMBO J. 2002; 21:3598–3607.

71. Harris AL, Contreras JE. Motifs in the permeation pathway of connexin channels mediate voltage and Ca (2+) sensing. Front Physiol. 2014; 5:113.
73. Weinan E, Vanden-Eijnden E. Towards a theory of transition paths. J Stat Phys. 2006; 123:503–523.

74. Tang Q, Dowd TL, Verselis VK, Bargiello TA. Conformational changes in a pore-forming region underlie voltage-dependent "loop gating" of an unapposed connexin hemichannel. J Gen Physiol. 2009; 133:555–570.

75. Verselis VK, Trelles MP, Rubinos C, Bargiello TA, Srinivas M. Loop gating of connexin hemichannels involves movement of pore-lining residues in the first extracellular loop domain. J Biol Chem. 2009; 284:4484–4493.

76. Holmgren M, Shin KS, Yellen G. The activation gate of a voltage-gated K+ channel can be trapped in the open state by an intersubunit metal bridge. Neuron. 1998; 21:617–621.

77. Nightingale ER Jr. Phenomenological theory of ion solvation. effective radii of hydrated ions. J Phys Chem. 1959; 63:1381–1387.

78. Kwon T, Roux B, Jo S, Klauda JB, Harris AL, Bargiello TA. Molecular dynamics simulations of the Cx26 hemichannel: insights into voltage-dependent loop-gating. Biophys J. 2012; 102:1341–1351.

79. Zonta F, Polles G, Zanotti G, Mammano F. Permeation pathway of homomeric connexin 26 and connexin 30 channels investigated by molecular dynamics. J Biomol Struct Dyn. 2012; 29:985–998.

80. Araya-Secchi R, Perez-Acle T, Kang SG, Huynh T, Bernardin A, Escalona Y, et al. Characterization of a novel water pocket inside the human Cx26 hemichannel structure. Biophys J. 2014; 107:599–612.

81. Bennett B, Purdy M, Baker K, McIntire W, Stevens R, Zhang Q, et al. X-ray structure of the Cx26 gap junction channel and comparison with the Cryo-EM structure of Cx43. Biophys J. 2013; 104:Suppl 1. 42a–43a.

82. Im W, Seefeld S, Roux B. A Grand Canonical Monte Carlo-Brownian dynamics algorithm for simulating ion channels. Biophys J. 2000; 79:788–801.

83. Noskov SY, Im W, Roux B. Ion permeation through the alpha-hemolysin channel: theoretical studies based on Brownian dynamics and Poisson-Nernst-Plank electrodiffusion theory. Biophys J. 2004; 87:2299–2309.

84. Roux B, Allen T, Bernèche S, Im W. Theoretical and computational models of biological ion channels. Q Rev Biophys. 2004; 37:15–103.

85. Lee KI, Rui H, Pastor RW, Im W. Brownian dynamics simulations of ion transport through the VDAC. Biophys J. 2011; 100:611–619.

86. Khalili-Araghi F, Jogini V, Yarov-Yarovoy V, Tajkhorshid E, Roux B, Schulten K. Calculation of the gating charge for the Kv1.2 voltage-activated potassium channel. Biophys J. 2010; 98:2189–2198.





 PDF
PDF ePub
ePub Citation
Citation Print
Print


 XML Download
XML Download