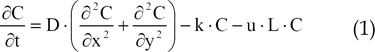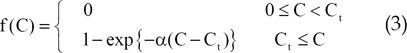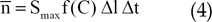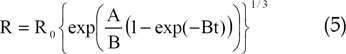1. Folkman J. Angiogenesis in cancer, vascular, rheumatoid and other disease. Nat Med. 1995. 1:21–31.
2. Chaplain MAJ. Avascular growth, angiogenesis and vascular growth in solid tumours: the mathematical modelling of the stages of tumour development. Math Comput Model. 1996. 23:47–87.
3. Chaplain MAJ, Anderson ARA. The mathematical modelling, simulation and prediction of tumour-induced angiogenesis. Invasion Metastasis. 1997. 16:222–234.
4. Gazit Y, Berk DA, Leunig M, Baxter LT, Jain RK. Scale-invariant behavior and vascular network formation in normal and tumor tissue. Phys Rev Lett. 1995. 75:2428–2431.
5. Tong S, Yuan F. Numerical simulations of angiogenesis in the cornea. Microvasc Res. 2001. 61:14–27.
6. Kansal AR, Torquato S, Harsh GR, Chiocca EA, Deisboeck TS. Simulated brain tumor growth dynamics using a three-dimensional cellular automation. J Theor Biol. 2000. 203:1–18.
7. Takahashi JA, Fukumuto M, Igarashi K, Oda Y, Kikuchi H, Hatanaka M. Correlation of basic fibroblast growth factor expression levels with the degree of malignancy and vascularity in human gliomas. J Neurosurg. 1992. 76:792–798.
8. Zagzag D, Miller DC, Sato Y, Rifkin DB, Burstein DE. Immunohistochemical localization of basic fibroblast growth factor in astrocytomas. Cancer Res. 1990. 50:7393–7398.
9. Sato Y, Murphy PR, Sato R, Friesen HG. Fibroblast growth factor release by bovine endothelial cells and human astrocytoma cells in culture is density dependent. Mol Endocrinol. 1989. 3:744–748.
10. Kershaw D. The incomplete Cholesky-conjugate gradient method for the iterative solution of linear equations. J Comput Phys. 1978. 26:43–65.
11. Stokes CL, Lauffenburger DA. Analysis of the roles of microvessel endothelial cell random motility and chemotaxis in angiogenesis. J Theor Biol. 1991. 152:377–403.