INTRODUCTION
Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) is considered a useful tool for evaluating angiogenic alterations in various disease entities. As an advanced analysis technique, pharmacokinetic (PK)-modeling on DCE-MRI can quantify the functional status of vessels, such as transvascular permeability and blood volume. Given this advantage, PK parameters using DCE-MRI are predicted to be promising biomarkers for assessing the response to antiangiogenic treatment (
123).
In order to accept the DCE-MRI-derived PK parameters as relevant indicators for predicting treatment response and patient prognosis, their measurement accuracy and reliability must necessarily be satisfied. In this regard, some steps in PK modeling have potential risks for significant misestimating (
4). In particular, flip angle (FA) deviation due to a defectively transmitted radiofrequency field results in incorrect quantifications of the pre-contrast R
1 and the Gd-driven contrast enhancement ratio (CER). As these two values are crucial elements in converting the DCE-MRI signal to the Gd-concentration for PK modeling (
5678), such miscalculation eventually leads to inaccurate and non-reproducible estimation of PK parameters (
791011).
Such unfavorable influence of B
1-inhomogeneity on PK modeling of DCE-MRI has been demonstrated in many reports (
5678). However, the degree of error propagation led by the FA fluctuation in each modeling step has not been evaluated. This detailed information is important for establishing a strategy to minimize the measurement error and for understating the principle of error transfer and/or augmentation between the PK modeling processes. From this perspective, this study was conducted to investigate the actual range of B
1-inhomogeneity and its impact on each computational process in PK modeling. Specifically, real FA variation measured on a clinical 3T MRI unit is applied to the Monte Carlo simulation that describes the B
1-dependent, erroneous PK parameter estimation. Additionally, the extent of FA inhomogeneity is measured in normal volunteers in order to predict the FA-error-induced inaccuracy of PK parameters in clinical situations. Finally, the strategy to reduce such undesirable effects of B
1-inhomogeneity on PK modeling is discussed.
Go to :

DISCUSSION
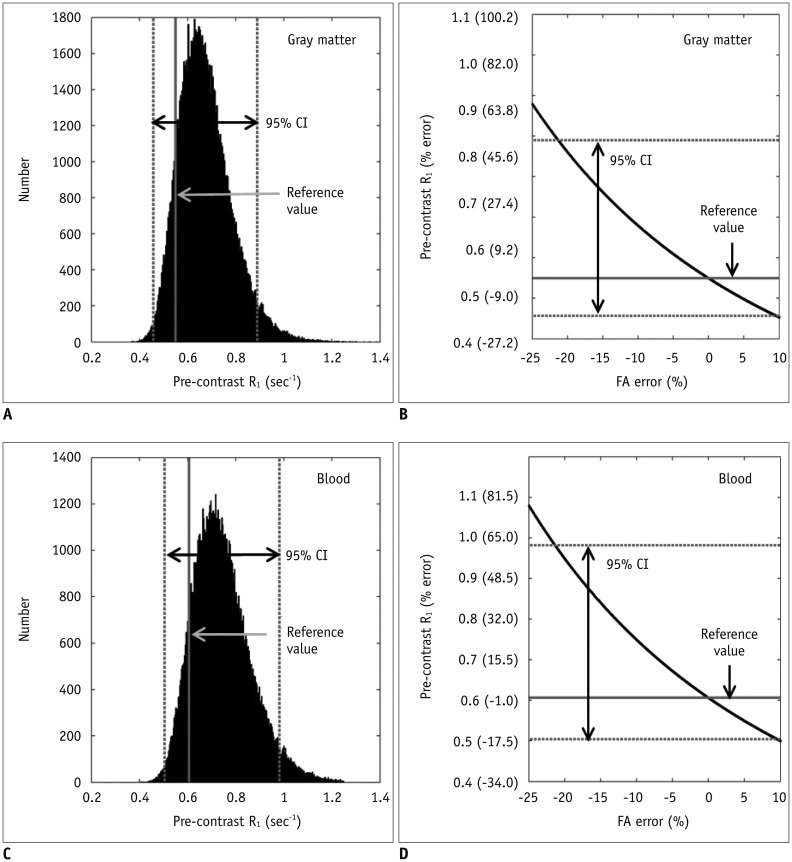
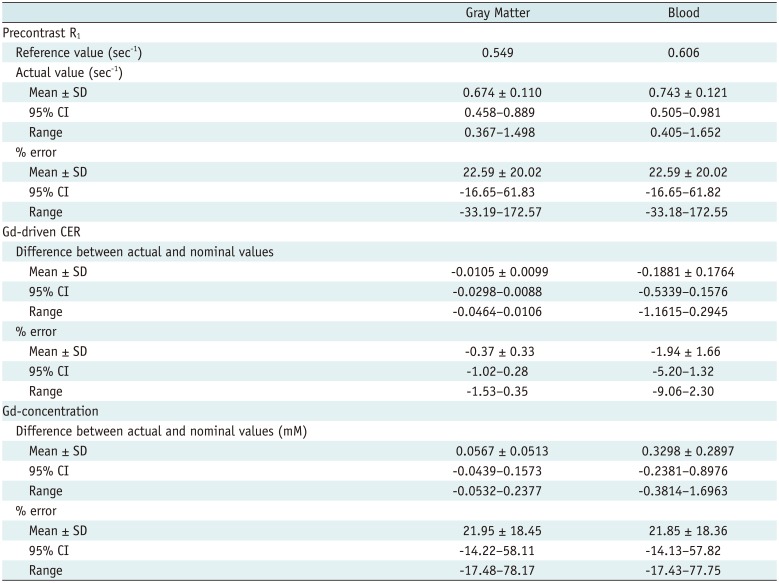
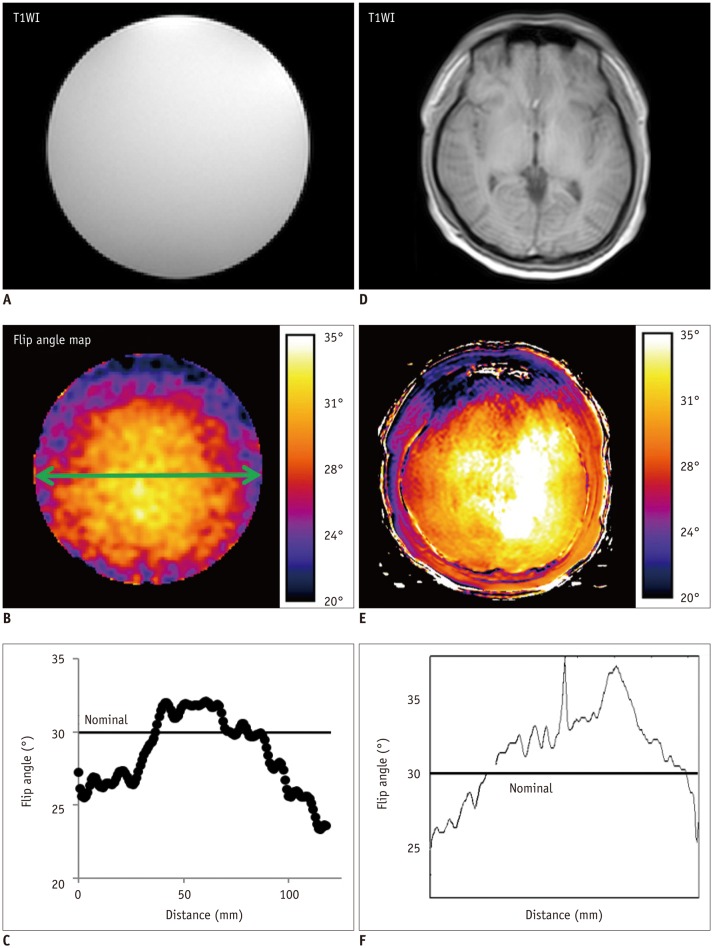
This study analyzed the influence of B
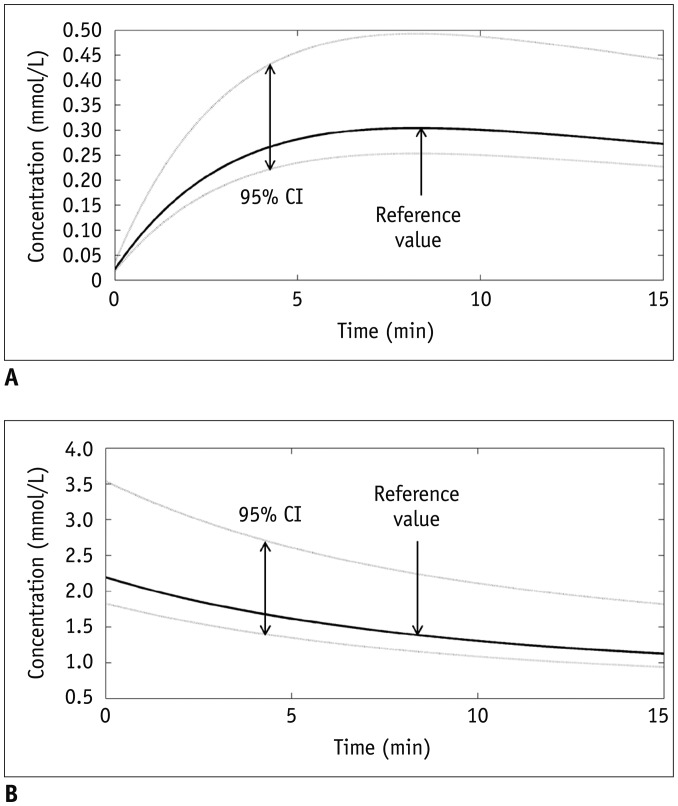
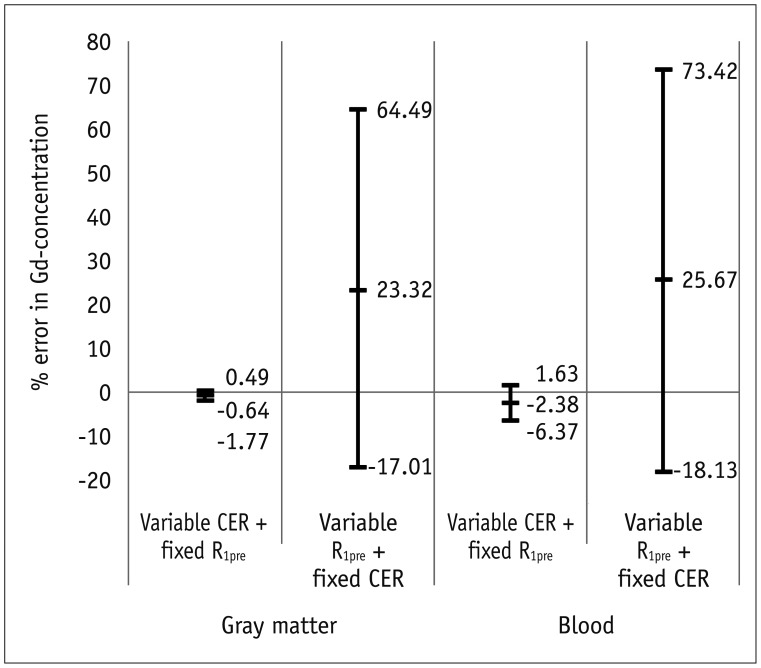
1-inhomogeneity on the PK modeling of DCE-MRI. In the phantom experiment on a 3T unit that undergoes regular vendor-guided equipment maintenance, a considerable range was observed in the actual FA (95% CI, −23–5%) with a nominal FA of 30°. Subsequently, Monte Carlo simulation using a similar FA variation demonstrated that the B
1-inhomogeneity-induced incorrect measurement of pre-contrast R
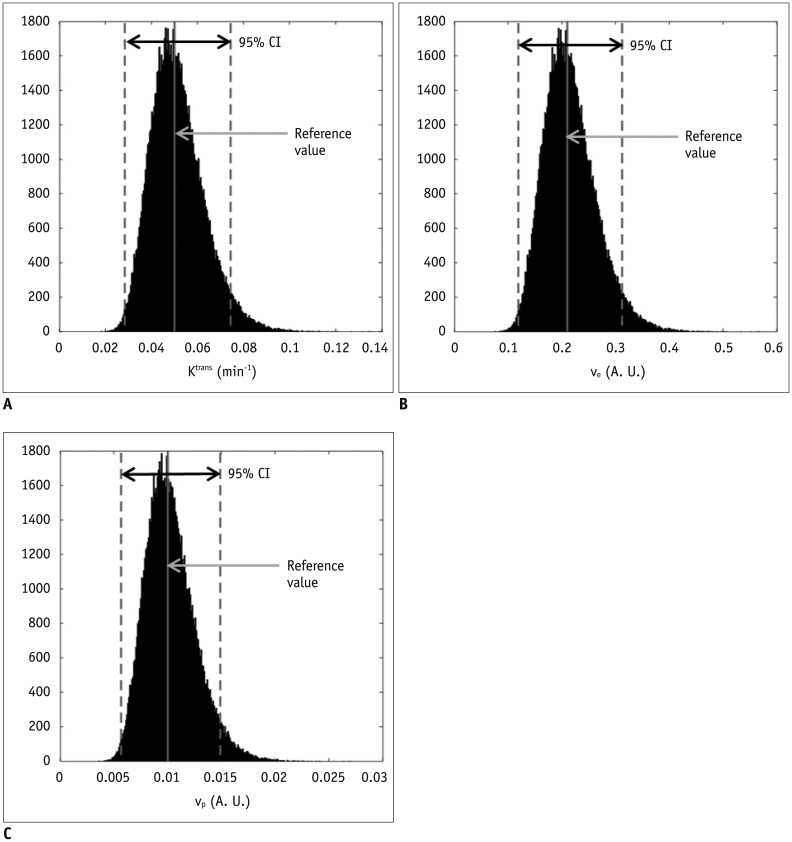
1 (−17–62%) as well as the Gd-driven CER (−5–1%) led to a substantial deviation of the Gd-concentration (−14–58%). Finally, our simulation demonstrated a significant variation in the PK parameters (−43–49%), which would be beyond a tolerable error range in clinical practice (
16).
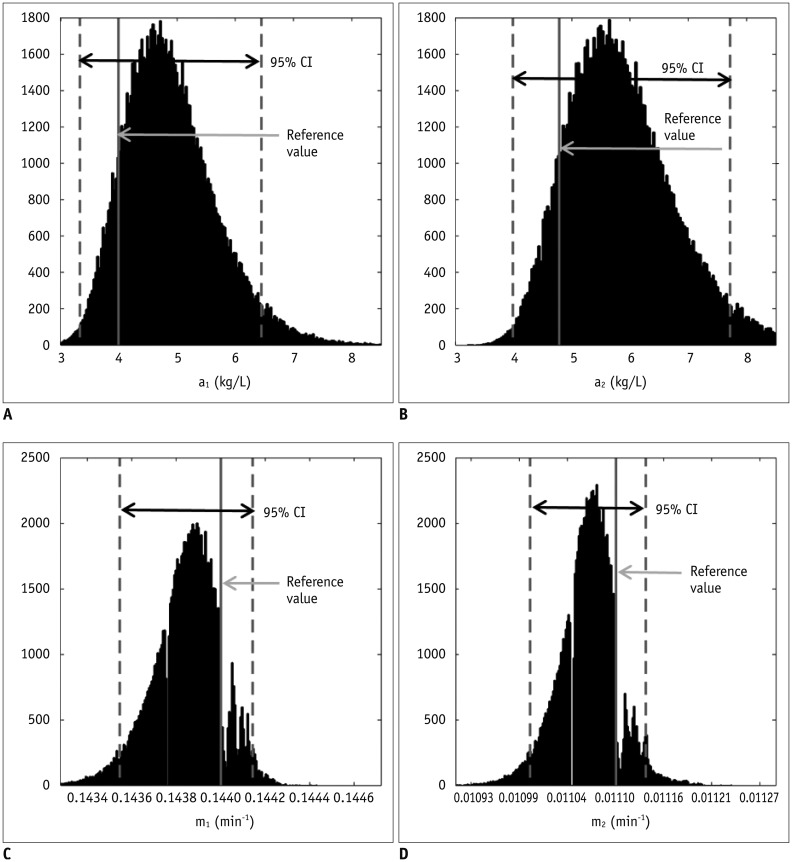
According to our simulation, the FA variation has a greater effect on the pre-contrast R
1 measurement than on the CER. In this respect, a -10% FA deviation caused a 23.6% R
1 error but only a −0.4% CER error in the gray matter. We suggest that this strong vulnerability of the pre-contrast R
1 to FA inhomogeneity is closely related to the calculation process in the VFA method. According to the Eq-4 and TR of 5 msec,
R1=1TR·In(1m)=10.0025·In(1m)=400·In(1m)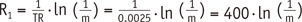
. As such, multiplication of
1TR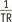
, i.e., 400, amplifies a small variation of ‘m’ to a substantial error of R
1. For example in our simulation, only a −0.03% deviation of ‘m’ led to a 23.6% error of R
1. Moreover, as the pre-contrast R
1 is used from the first step in converting the DCE-MRI SI to the Gd-concentration, its deviation continuously affects the subsequent calculations in the PK modeling. As shown in our simulation example, a 23.6% deviation of blood pre-contrast R
1, which was induced by a −10% FA error, ultimately causes approximately −24% deviations of K
trans, v
e, and v
p. Therefore, in order to improve the accuracy and reliability of PK parameter measurements, it is necessary to control the propagation of R
1 error throughout a number of steps in the Gd-concentration estimation.
In order to reduce the undesirable effect of B
1-inhomogeneity on estimation of PK parameters, the application of B
1-corrected R
1 mapping is the primary recommended solution (
2021). In a recent study the B
1 field was accurately homogenized by a linear, inverse, distant-weighted interpolation. This study demonstrated that this B
1 correction could reduce the difference in the
in vivo T
1 value, between the inversion recovery and VFA methods, from 58% to 8.1% in the breast coil(
21). According to Eq-3 and -4, such an 8.1% R
1 error is approximately equivalent to an FA error of 4%. Therefore, the B
1 correction can reduce not only the R
1 deviation but also the CER error, thereby significantly improving the quality of PK modeling.
Applying a long TR in a condition that satisfies the acceptable scanning time can be another solution for reducing the variation of pre-contrast R
1. Our simulation used a TR of 2.5 msec for the VFA method as recommended by the QIBA guidelines when using the same pulse sequence for R
1 measurement as used for the DCE-MRI (
16). However, as detailed in Eq-4, the use of a longer TR can reduce the effect of deviated ‘m’ while not disturbing the PK modeling. For example, a TR of 5 msec may reduce the effect of deviated ‘ln (1 / m)’ by half compared with a TR of 2.5 msec.
A majority of two-compartment models analyze the shape of the time-concentration curve, and therefore are strongly dependent on the accuracy of the Gd-concentration. Therefore, these methods are inherently affected by the FA-dependent error, as described above. On the other hand, an algorithm that was initially proposed by Brix et al. (
22) and then modified by Hoffmann et al. (
23) estimates PK parameters directly from the DCE-MRI SI. Therefore, this method has an important advantage to avoid potential errors occurring during the measurement of pre-contrast R
1 and Gd-concentration. The feasibility of this simple approach as an alternative to the complex, two-compartment models has been validated in several clinical trials (
22242526). Another benefit of this method is that there is no requirement for AIF measurement which has been seriously considered as a major error source in PK modeling (
27). However, the usage of this algorithm is acceptable only under specific permeability-limiting conditions (
1728), and does not provide the blood volume. Therefore, a larger-scale verification regarding its strength and weakness is necessary, which must be based on a comparison with the concentration-based, two-compartment models.
In the present study, the B
1-inhomogeneity was measured using a brain coil. As the B
1-inhomogeneity increases in a larger field of view, the FA variation must be greater in the body and breast coils than in the brain coil. Actually, previous breast coil studies showed a wider deviation of FA (median, −40%; and greater than −50% in some cases) than this study (
710). Consequently, the variation of FA and the subsequent measurement error of PK parameters may be augmented when using the breast or body coil.
The influence of B
1-inhomogeneity on PK parameter estimation from DCE-MRI was also simulated by Di Giovanni et al. (
9) who showed a greater variation of the PK parameters than that seen in our study (for example, K
trans and v
e error up to 531% and 233%). For the simulation, they separately employed the deviated pre-contrast R
1 and FA for DCE-MRI, which referred to the values seen in the literature reports. In contrast, our simulation applied such parameters originating from a single B
1-inhomogeneity condition on the basis of a phantom experiment, and therefore may be more realistic for predicting an error occurring in each MRI unit. Moreover, again comparing with Di Giovanni et al. (
9), this simulation included the deviation of AIF induced by FA error, and used the modified Tofts model that measures the v
p. Although the etiology and phenomenon of unstable PK modeling are similarly considered, the dissimilar simulation setting seems to be the main cause of such different error ranges in the PK parameters from different studies.
In conclusion, this study demonstrates the influences of B1-inhomogeneity on PK parameter estimation using DCE-MRI. An understanding of the inherent FA error, which occurs even in clinically utilized MR units and its impact on PK modeling, will help to establish strategies for using DCE-MRI to improve the quantification of disease- or treatment-driven vascular alterations.
Go to :

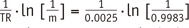 ), the small error of ‘m’ was increased to a 23.6% R1 deviation.
), the small error of ‘m’ was increased to a 23.6% R1 deviation.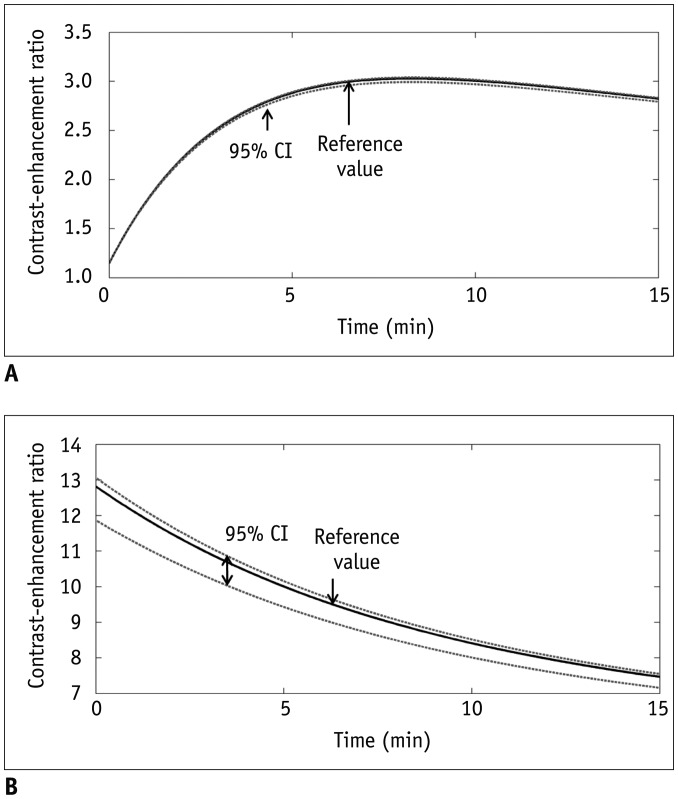
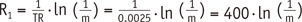 . As such, multiplication of 1TR
. As such, multiplication of 1TR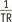 , i.e., 400, amplifies a small variation of ‘m’ to a substantial error of R1. For example in our simulation, only a −0.03% deviation of ‘m’ led to a 23.6% error of R1. Moreover, as the pre-contrast R1 is used from the first step in converting the DCE-MRI SI to the Gd-concentration, its deviation continuously affects the subsequent calculations in the PK modeling. As shown in our simulation example, a 23.6% deviation of blood pre-contrast R1, which was induced by a −10% FA error, ultimately causes approximately −24% deviations of Ktrans, ve, and vp. Therefore, in order to improve the accuracy and reliability of PK parameter measurements, it is necessary to control the propagation of R1 error throughout a number of steps in the Gd-concentration estimation.
, i.e., 400, amplifies a small variation of ‘m’ to a substantial error of R1. For example in our simulation, only a −0.03% deviation of ‘m’ led to a 23.6% error of R1. Moreover, as the pre-contrast R1 is used from the first step in converting the DCE-MRI SI to the Gd-concentration, its deviation continuously affects the subsequent calculations in the PK modeling. As shown in our simulation example, a 23.6% deviation of blood pre-contrast R1, which was induced by a −10% FA error, ultimately causes approximately −24% deviations of Ktrans, ve, and vp. Therefore, in order to improve the accuracy and reliability of PK parameter measurements, it is necessary to control the propagation of R1 error throughout a number of steps in the Gd-concentration estimation.



 PDF
PDF ePub
ePub Citation
Citation Print
Print



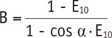
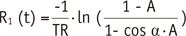
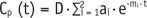
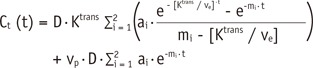
 XML Download
XML Download