1. Fisher AB, Chien S, Barakat AI, Nerem RM. Endothelial cellular response to altered shear stress. Am J Physiol Lung Cell Mol Physiol. 2001; 281:L529–L533.
2. Ku DN, Giddens DP, Zarins CK, Glagov S. Pulsatile flow and atherosclerosis in the human carotid bifurcation. Positive correlation between plaque location and low oscillating shear stress. Arteriosclerosis. 1985; 5:293–302.
3. Barker AJ, Markl M, Bürk J, Lorenz R, Bock J, Bauer S, et al. Bicuspid aortic valve is associated with altered wall shear stress in the ascending aorta. Circ Cardiovasc Imaging. 2012; 5:457–466.
4. Bissell MM, Hess AT, Biasiolli L, Glaze SJ, Loudon M, Pitcher A, et al. Aortic dilation in bicuspid aortic valve disease: flow pattern is a major contributor and differs with valve fusion type. Circ Cardiovasc Imaging. 2013; 6:499–507.
5. Uretsky S, Gillam LD. Nature versus nurture in bicuspid aortic valve aortopathy: more evidence that altered hemodynamics may play a role. Circulation. 2014; 129:622–624.
6. Slager CJ, Wentzel JJ, Gijsen FJ, Thury A, van der Wal AC, Schaar JA, et al. The role of shear stress in the destabilization of vulnerable plaques and related therapeutic implications. Nat Clin Pract Cardiovasc Med. 2005; 2:456–464.
7. Groen HC, Gijsen FJ, van der Lugt A, Ferguson MS, Hatsukami TS, van der Steen AF, et al. Plaque rupture in the carotid artery is localized at the high shear stress region: a case report. Stroke. 2007; 38:2379–2381.
8. Markl M, Kilner PJ, Ebbers T. Comprehensive 4D velocity mapping of the heart and great vessels by cardiovascular magnetic resonance. J Cardiovasc Magn Reson. 2011; 13:7.
9. Harloff A, Nussbaumer A, Bauer S, Stalder AF, Frydrychowicz A, Weiller C, et al. In vivo assessment of wall shear stress in the atherosclerotic aorta using flow-sensitive 4D MRI. Magn Reson Med. 2010; 63:1529–1536.
10. Markl M, Frydrychowicz A, Kozerke S, Hope M, Wieben O. 4D flow MRI. J Magn Reson Imaging. 2012; 36:1015–1036.
11. Morbiducci U, Ponzini R, Rizzo G, Cadioli M, Esposito A, De Cobelli F, et al. In vivo quantification of helical blood flow in human aorta by time-resolved three-dimensional cine phase contrast magnetic resonance imaging. Ann Biomed Eng. 2009; 37:516–531.
12. Harloff A, Albrecht F, Spreer J, Stalder AF, Bock J, Frydrychowicz A, et al. 3D blood flow characteristics in the carotid artery bifurcation assessed by flow-sensitive 4D MRI at 3T. Magn Reson Med. 2009; 61:65–74.
3. Bammer R, Hope TA, Aksoy M, Alley MT. Time-resolved 3D quantitative flow MRI of the major intracranial vessels: initial experience and comparative evaluation at 1.5T and 3.0T in combination with parallel imaging. Magn Reson Med. 2007; 57:127–140.
14. Hsiao A, Tariq U, Alley MT, Lustig M, Vasanawala SS. Inlet and outlet valve flow and regurgitant volume may be directly and reliably quantified with accelerated, volumetric phase-contrast MRI. J Magn Reson Imaging. 2015; 41:376–385.
15. Petersson S, Sigfridsson A, Dyverfeldt P, Carlhäll CJ, Ebbers T. Retrospectively gated intracardiac 4D flow MRI using spiral trajectories. Magn Reson Med. 2016; 75:196–120.
16. Dyverfeldt P, Gårdhagen R, Sigfridsson A, Karlsson M, Ebbers T. On MRI turbulence quantification. Magn Reson Imaging. 2009; 27:913–992.
17. Dyverfeldt P, Hope MD, Tseng EE, Saloner D. Magnetic resonance measurement of turbulent kinetic energy for the estimation of irreversible pressure loss in aortic stenosis. JACC Cardiovasc Imaging. 2013; 6:64–71.
18. Dyverfeldt P, Kvitting JP, Sigfridsson A, Engvall J, Bolger AF, Ebbers T. Assessment of fluctuating velocities in disturbed cardiovascular blood flow: in vivo feasibility of generalized phase-contrast MRI. J Magn Reson Imaging. 2008; 28:655–663.
19. Kim GB, Ha H, Kweon J, Lee SJ, Kim YH, Yang DH, et al. Post-stenotic plug-like jet with a vortex ring demonstrated by 4D flow MRI. Magn Reson Imaging. 2016; 34:371–375.
20. von Spiczak J, Crelier G, Giese D, Kozerke S, Maintz D, Bunck AC. Quantitative analysis of vortical blood flow in the thoracic aorta using 4D phase contrast MRI. PLoS One. 2015; 10:e0139025.
21. Donati F, Figueroa CA, Smith NP, Lamata P, Nordsletten DA. Non-invasive pressure difference estimation from PC-MRI using the work-energy equation. Med Image Anal. 2015; 26:159–172.
22. Ebbers T, Wigström L, Bolger AF, Engvall J, Karlsson M. Estimation of relative cardiovascular pressures using time-resolved three-dimensional phase contrast MRI. Magn Reson Med. 2001; 45:872–879.
23. Krittian SB, Lamata P, Michler C, Nordsletten DA, Bock J, Bradley CP, et al. A finite-element approach to the direct computation of relative cardiovascular pressure from time-resolved MR velocity data. Med Image Anal. 2012; 16:1029–1037.
24. Markl M, Wallis W, Brendecke S, Simon J, Frydrychowicz A, Harloff A. Estimation of global aortic pulse wave velocity by flow-sensitive 4D MRI. Magn Reson Med. 2010; 63:1575–1582.
25. Markl M, Wallis W, Strecker C, Gladstone BP, Vach W, Harloff A. Analysis of pulse wave velocity in the thoracic aorta by flow-sensitive four-dimensional MRI: reproducibility and correlation with characteristics in patients with aortic atherosclerosis. J Magn Reson Imaging. 2012; 35:1162–1168.
26. Pelc NJ, Bernstein MA, Shimakawa A, Glover GH. Encoding strategies for three-direction phase-contrast MR imaging of flow. J Magn Reson Imaging. 1991; 1:405–413.
27. Bernstein MA, Ikezaki Y. Comparison of phase-difference and complex-difference processing in phase-contrast MR angiography. J Magn Reson Imaging. 1991; 1:725–729.
28. Dumoulin CL, Souza SP, Walker MF, Wagle W. Three-dimensional phase contrast angiography. Magn Reson Med. 1989; 9:139–149.
29. Hofman MB, Visser FC, van Rossum AC, Vink QM, Sprenger M, Westerhof N. In vivo validation of magnetic resonance blood volume flow measurements with limited spatial resolution in small vessels. Magn Reson Med. 1995; 33:778–784.
30. Dyverfeldt P, Bissell M, Barker AJ, Bolger AF, Carlhäll CJ, Ebbers T, et al. 4D flow cardiovascular magnetic resonance consensus statement. J Cardiovasc Magn Reson. 2015; 17:72.
31. Frydrychowicz A, Berger A, Munoz Del Rio A, Russe MF, Bock J, Harloff A, et al. Interdependencies of aortic arch secondary flow patterns, geometry, and age analysed by 4-dimensional phase contrast magnetic resonance imaging at 3 Tesla. Eur Radiol. 2012; 22:1122–1130.
32. Meckel S, Leitner L, Bonati LH, Santini F, Schubert T, Stalder AF, et al. Intracranial artery velocity measurement using 4D PC MRI at 3 T: comparison with transcranial ultrasound techniques and 2D PC MRI. Neuroradiology. 2013; 55:389–398.
33. Rivera-Rivera LA, Turski P, Johnson KM, Hoffman C, Berman SE, Kilgas P, et al. 4D flow MRI for intracranial hemodynamics assessment in Alzheimer's disease. J Cereb Blood Flow Metab. 2015; 11. 25. DOI:
10.1177/0271678X15617171. [Epub].
34. Schrauben E, Wåhlin A, Ambarki K, Spaak E, Malm J, Wieben O, et al. Fast 4D flow MRI intracranial segmentation and quantification in tortuous arteries. J Magn Reson Imaging. 2015; 42:1458–1464.
35. Strecker C, Harloff A, Wallis W, Markl M. Flow-sensitive 4D MRI of the thoracic aorta: comparison of image quality, quantitative flow, and wall parameters at 1.5 T and 3 T. J Magn Reson Imaging. 2012; 36:1097–1110.
36. Bernstein MA, Zhou XJ, Polzin JA, King KF, Ganin A, Pelc NJ, et al. Concomitant gradient terms in phase contrast MR: analysis and correction. Magn Reson Med. 1998; 39:300–308.
37. Markl M, Bammer R, Alley MT, Elkins CJ, Draney MT, Barnett A, et al. Generalized reconstruction of phase contrast MRI: analysis and correction of the effect of gradient field distortions. Magn Reson Med. 2003; 50:791–801.
38. Walker PG, Cranney GB, Scheidegger MB, Waseleski G, Pohost GM, Yoganathan AP. Semiautomated method for noise reduction and background phase error correction in MR phase velocity data. J Magn Reson Imaging. 1993; 3:521–530.
39. Abdul-Rahman HS, Gdeisat MA, Burton DR, Lalor MJ, Lilley F, Moore CJ. Fast and robust three-dimensional best path phase unwrapping algorithm. Appl Opt. 2007; 46:6623–6635.
40. Chavez S, Xiang QS, An L. Understanding phase maps in MRI: a new cutline phase unwrapping method. IEEE Trans Med Imaging. 2002; 21:966–977.
41. Jenkinson M. Fast, automated, N-dimensional phase-unwrapping algorithm. Magn Reson Med. 2003; 49:193–197.
42. Salfity MF, Huntley JM, Graves MJ, Marklund O, Cusack R, Beauregard DA. Extending the dynamic range of phase contrast magnetic resonance velocity imaging using advanced higher-dimensional phase unwrapping algorithms. J R Soc Interface. 2006; 3:415–427.
43. Salfity MF, Ruiz PD, Huntley JM, Graves MJ, Cusack R, Beauregard DA. Branch cut surface placement for unwrapping of undersampled three-dimensional phase data: application to magnetic resonance imaging arterial flow mapping. Appl Opt. 2006; 45:2711–2722.
44. Szumowski J, Coshow WR, Li F, Quinn SF. Phase unwrapping in the three-point Dixon method for fat suppression MR imaging. Radiology. 1994; 192:555–561.
45. Bustamante M, Petersson S, Eriksson J, Alehagen U, Dyverfeldt P, Carlhäll CJ, et al. Atlas-based analysis of 4D flow CMR: automated vessel segmentation and flow quantification. J Cardiovasc Magn Reson. 2015; 17:87.
46. van Pelt R, Oliván Bescós J, Breeuwer M, Clough RE, Gröller ME, ter Haar Romenij B, et al. Exploration of 4D MRI blood flow using stylistic visualization. IEEE Trans Vis Comput Graph. 2010; 16:1339–1347.
47. van Pelt R, Nguyen H, ter Haar Romeny B, Vilanova A. Automated segmentation of blood-flow regions in large thoracic arteries using 3D-cine PC-MRI measurements. Int J Comput Assist Radiol Surg. 2012; 7:217–224.
48. Bagan P, Vidal R, Martinod E, Destable MD, Tremblay B, Dumas JL, et al. Cerebral ischemia during carotid artery cross-clamping: predictive value of phase-contrast magnetic resonance imaging. Ann Vasc Surg. 2006; 20:747–752.
49. Hope TA, Hope MD, Purcell DD, von Morze C, Vigneron DB, Alley MT, et al. Evaluation of intracranial stenoses and aneurysms with accelerated 4D flow. Magn Reson Imaging. 2010; 28:41–46.
50. Garcia J, Barker AJ, van Ooij P, Schnell S, Puthumana J, Bonow RO, et al. Assessment of altered three-dimensional blood characteristics in aortic disease by velocity distribution analysis. Magn Reson Med. 2015; 74:817–825.
51. Markl M, Chan FP, Alley MT, Wedding KL, Draney MT, Elkins CJ, et al. Time-resolved three-dimensional phase-contrast MRI. J Magn Reson Imaging. 2003; 17:499–506.
52. Stalder AF, Russe MF, Frydrychowicz A, Bock J, Hennig J, Markl M. Quantitative 2D and 3D phase contrast MRI: optimized analysis of blood flow and vessel wall parameters. Magn Reson Med. 2008; 60:1218–1231.
53. Mathieu J, Scott J. An introduction to turbulent flow. Cambridge: Cambridge University Press;2000. p. 10–11.
54. Dyverfeldt P, Sigfridsson A, Kvitting JP, Ebbers T. Quantification of intravoxel velocity standard deviation and turbulence intensity by generalizing phase-contrast MRI. Magn Reson Med. 2006; 56:850–858.
55. Wong KK, Kelso RM, Worthley SG, Sanders P, Mazumdar J, Abbott D. Cardiac flow analysis applied to phase contrast magnetic resonance imaging of the heart. Ann Biomed Eng. 2009; 37:1495–1515.
56. Elbaz MS, Calkoen EE, Westenberg JJ, Lelieveldt BP, Roest AA, van der Geest RJ. Vortex flow during early and late left ventricular filling in normal subjects: quantitative characterization using retrospectively-gated 4D flow cardiovascular magnetic resonance and three-dimensional vortex core analysis. J Cardiovasc Magn Reson. 2014; 16:78.
57. Reiter G, Reiter U, Kovacs G, Olschewski H, Fuchsjäger M. Blood flow vortices along the main pulmonary artery measured with MR imaging for diagnosis of pulmonary hypertension. Radiology. 2015; 275:71–79.
58. Jeong J, Hussain F. On the identification of a vortex. J Fluid Mech. 1995; 285:69–94.
59. Zhou J, Adrian RJ, Balachandar S. Autogeneration of near-wall vortical structures in channel flow. Phys Fluids. 1996; 8:288–290.
60. Zhou J, Adrian RJ, Balachandar S, Kendall TM. Mechanisms for generating coherent packets of hairpin vortices in channel flow. J Fluid Mech. 1999; 387:353–396.
61. Adrian RJ, Christensen KT, Liu ZC. Analysis and interpretation of instantaneous turbulent velocity fields. Exp Fluids. 2000; 29:275–290.
62. Currie PJ, Seward JB, Reeder GS, Vlietstra RE, Bresnahan DR, Bresnahan JF, et al. Continuous-wave Doppler echocardiographic assessment of severity of calcific aortic stenosis: a simultaneous Doppler-catheter correlative study in 100 adult patients. Circulation. 1985; 71:1162–1169.
63. Cohn JN, Quyyumi AA, Hollenberg NK, Jamerson KA. Surrogate markers for cardiovascular disease: functional markers. Circulation. 2004; 109:25 Suppl 1. IV31–IV46.
64. Stamm RB, Martin RP. Quantification of pressure gradients across stenotic valves by Doppler ultrasound. J Am Coll Cardiol. 1983; 2:707–718.
65. Bock J, Frydrychowicz A, Lorenz R, Hirtler D, Barker AJ, Johnson KM, et al. In vivo noninvasive 4D pressure difference mapping in the human aorta: phantom comparison and application in healthy volunteers and patients. Magn Reson Med. 2011; 66:1079–1088.
66. Ebbers T, Farnebäck G. Improving computation of cardiovascular relative pressure fields from velocity MRI. J Magn Reson Imaging. 2009; 30:54–61.
67. Hope MD, Meadows AK, Hope TA, Ordovas KG, Saloner D, Reddy GP, et al. Clinical evaluation of aortic coarctation with 4D flow MR imaging. J Magn Reson Imaging. 2010; 31:711–718.
68. Roes SD, Hammer S, van der Geest RJ, Marsan NA, Bax JJ, Lamb HJ, et al. Flow assessment through four heart valves simultaneously using 3-dimensional 3-directional velocity-encoded magnetic resonance imaging with retrospective valve tracking in healthy volunteers and patients with valvular regurgitation. Invest Radiol. 2009; 44:669–675.
69. Eriksson J, Bolger AF, Ebbers T, Carlhäll CJ. Four-dimensional blood flow-specific markers of LV dysfunction in dilated cardiomyopathy. Eur Heart J Cardiovasc Imaging. 2013; 14:417–424.
70. Calkoen EE, Roest AA, Kroft LJ, van der Geest RJ, Jongbloed MR, van den Boogaard PJ, et al. Characterization and improved quantification of left ventricular inflow using streamline visualization with 4DFlow MRI in healthy controls and patients after atrioventricular septal defect correction. J Magn Reson Imaging. 2015; 41:1512–1520.
71. Hope MD, Hope TA, Crook SE, Ordovas KG, Urbania TH, Alley MT, et al. 4D flow CMR in assessment of valve-related ascending aortic disease. JACC Cardiovasc Imaging. 2011; 4:781–787.
72. Berg P, Stucht D, Janiga G, Beuing O, Speck O, Thévenin D. Cerebral blood flow in a healthy Circle of Willis and two intracranial aneurysms: computational fluid dynamics versus four-dimensional phase-contrast magnetic resonance imaging. J Biomech Eng. 2014; 136:041003.
73. Schnell S, Ansari SA, Vakil P, Wasielewski M, Carr ML, Hurley MC, et al. Three-dimensional hemodynamics in intracranial aneurysms: influence of size and morphology. J Magn Reson Imaging. 2014; 39:120–131.
74. Guzzardi DG, Barker AJ, van Ooij P, Malaisrie SC, Puthumana JJ, Belke DD, et al. Valve-related hemodynamics mediate human bicuspid aortopathy: insights from wall shear stress mapping. J Am Coll Cardiol. 2015; 66:892–900.
75. Jou LD, Lee DH, Morsi H, Mawad ME. Wall shear stress on ruptured and unruptured intracranial aneurysms at the internal carotid artery. AJNR Am J Neuroradiol. 2008; 29:1761–1767.
76. van Ooij P, Potters WV, Guédon A, Schneiders JJ, Marquering HA, Majoie CB, et al. Wall shear stress estimated with phase contrast MRI in an in vitro and in vivo intracranial aneurysm. J Magn Reson Imaging. 2013; 38:876–884.
77. Isoda H, Ohkura Y, Kosugi T, Hirano M, Takeda H, Hiramatsu H, et al. In vivo hemodynamic analysis of intracranial aneurysms obtained by magnetic resonance fluid dynamics (MRFD) based on time-resolved three-dimensional phase-contrast MRI. Neuroradiology. 2010; 52:921–928.
78. Zajac J, Eriksson J, Dyverfeldt P, Bolger AF, Ebbers T, Carlhäll CJ. Turbulent kinetic energy in normal and myopathic left ventricles. J Magn Reson Imaging. 2015; 41:1021–1029.
79. Tyszka JM, Laidlaw DH, Asa JW, Silverman JM. Three-dimensional, time-resolved (4D) relative pressure mapping using magnetic resonance imaging. J Magn Reson Imaging. 2000; 12:321–329.
80. Yang GZ, Kilner PJ, Wood NB, Underwood SR, Firmin DN. Computation of flow pressure fields from magnetic resonance velocity mapping. Magn Reson Med. 1996; 36:520–526.
81. Bley TA, Johnson KM, François CJ, Reeder SB, Schiebler ML, R Landgraf B, et al. Noninvasive assessment of transstenotic pressure gradients in porcine renal artery stenoses by using vastly undersampled phase-contrast MR angiography. Radiology. 2011; 261:266–273.
82. Lum DP, Johnson KM, Paul RK, Turk AS, Consigny DW, Grinde JR, et al. Transstenotic pressure gradients: measurement in swine--retrospectively ECG-gated 3D phase-contrast MR angiography versus endovascular pressure-sensing guidewires. Radiology. 2007; 245:751–760.
83. Moftakhar R, Aagaard-Kienitz B, Johnson K, Turski PA, Turk AS, Niemann DB, et al. Noninvasive measurement of intra-aneurysmal pressure and flow pattern using phase contrast with vastly undersampled isotropic projection imaging. AJNR Am J Neuroradiol. 2007; 28:1710–1714.
84. Wentland AL, Wieben O, François CJ, Boncyk C, Munoz Del Rio A, Johnson KM, et al. Aortic pulse wave velocity measurements with undersampled 4D flow-sensitive MRI: comparison with 2D and algorithm determination. J Magn Reson Imaging. 2013; 37:853–859.
85. Sigovan M, Hope MD, Dyverfeldt P, Saloner D. Comparison of four-dimensional flow parameters for quantification of flow eccentricity in the ascending aorta. J Magn Reson Imaging. 2011; 34:1226–1230.
86. Manka R, Busch J, Crelier G, Lüscher TF, Kozerke S. Pre- and post-operative assessment of valvular and aortic flow using 4D flow magnetic resonance imaging. Eur Heart J. 2013; 34:1423.
87. Schnell S, Markl M, Entezari P, Mahadewia RJ, Semaan E, Stankovic Z, et al. k-t GRAPPA accelerated four-dimensional flow MRI in the aorta: effect on scan time, image quality, and quantification of flow and wall shear stress. Magn Reson Med. 2014; 72:522–533.
88. Johnson KM, Lum DP, Turski PA, Block WF, Mistretta CA, Wieben O. Improved 3D phase contrast MRI with off-resonance corrected dual echo VIPR. Magn Reson Med. 2008; 60:1329–1336.
89. Kecskemeti S, Johnson K, Wu Y, Mistretta C, Turski P, Wieben O. High resolution three-dimensional cine phase contrast MRI of small intracranial aneurysms using a stack of stars k-space trajectory. J Magn Reson Imaging. 2012; 35:518–527.
90. Petersson S, Dyverfeldt P, Gårdhagen R, Karlsson M, Ebbers T. Simulation of phase contrast MRI of turbulent flow. Magn Reson Med. 2010; 64:1039–1046.
91. Yoon YE, Hong YJ, Kim HK, Kim JA, Na JO, Yang DH, et al. 2014 Korean guidelines for appropriate utilization of cardiovascular magnetic resonance imaging: a joint report of the Korean Society of Cardiology and the Korean Society of Radiology. Korean J Radiol. 2014; 15:659–688.
92. Park SH, Han PK, Choi SH. Physiological and functional magnetic resonance imaging using balanced steady-state free precession. Korean J Radiol. 2015; 16:550–559.
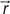 is the displacement, B0 is the static magnetic field, ΔB0 is the local field inhomogeneity, and
is the displacement, B0 is the static magnetic field, ΔB0 is the local field inhomogeneity, and 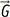 is the magnetic field gradient. Assuming that the fluid velocity
is the magnetic field gradient. Assuming that the fluid velocity 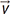 is constant during the acquisition, the displacement
is constant during the acquisition, the displacement 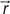 can be described as
can be described as  , where t0 is the excitation time and
, where t0 is the excitation time and 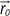 is the displacement at t0. Then, the phase shift of the fluid with the velocity
is the displacement at t0. Then, the phase shift of the fluid with the velocity 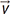 under the magnetic gradient can be obtained by integrating the ωL from t0 to the echo time (TE) as:
under the magnetic gradient can be obtained by integrating the ωL from t0 to the echo time (TE) as:
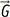 . The integral terms describing the influence of the magnetic gradient on the static and moving spins are named the zeroth and the first gradient moments, M0 and M1, respectively.
. The integral terms describing the influence of the magnetic gradient on the static and moving spins are named the zeroth and the first gradient moments, M0 and M1, respectively.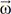 is defined as the curl of the velocity vector
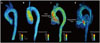
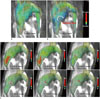
is defined as the curl of the velocity vector 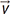 : where ∇ is the del operator. Here, each vorticity component indicates the swirling intensity of the fluid element along the corresponding axis (Fig. 6A). The unit of vorticity is s-1.
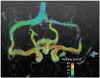
: where ∇ is the del operator. Here, each vorticity component indicates the swirling intensity of the fluid element along the corresponding axis (Fig. 6A). The unit of vorticity is s-1. . Then, the velocity gradient tensor can be decomposed into the symmetric S and asymmetric Ω terms as follows: where T indicates the transpose of the matrix. Identification of the eigenvalues of S2 + Ω2 for each voxel results in three eigenvalues, λ1, λ2, and λ3, where λ1 ≥ λ2 ≥ λ3. Finally, the vortex flow region can be found where λ2 is negative. Since this algorithm is Galilean invariant, the vortical flow structures can be identified even though the vortical flow is overlaid with the uniform translational velocity field.
. Then, the velocity gradient tensor can be decomposed into the symmetric S and asymmetric Ω terms as follows: where T indicates the transpose of the matrix. Identification of the eigenvalues of S2 + Ω2 for each voxel results in three eigenvalues, λ1, λ2, and λ3, where λ1 ≥ λ2 ≥ λ3. Finally, the vortex flow region can be found where λ2 is negative. Since this algorithm is Galilean invariant, the vortical flow structures can be identified even though the vortical flow is overlaid with the uniform translational velocity field.



 PDF
PDF ePub
ePub Citation
Citation Print
Print


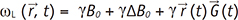
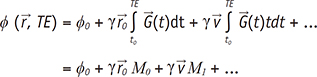
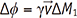
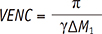

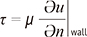

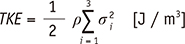
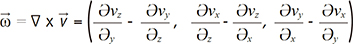
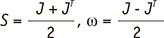
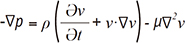





 XML Download
XML Download