Journal List > Korean J Radiol > v.16(2) > 1027099

TOOLS
Kim, Choi, Kim, Yun, Jahng, Jeong, and Kim: Effects of MR Parameter Changes on the Quantification of Diffusion Anisotropy and Apparent Diffusion Coefficient in Diffusion Tensor Imaging: Evaluation Using a Diffusional Anisotropic Phantom
Experimental and Others
Original Article

Korean Journal of Radiology 2015; 16(2): 297-303.

Published online: 27 February 2015

DOI: https://doi.org/10.3348/kjr.2015.16.2.297

Effects of MR Parameter Changes on the Quantification of Diffusion Anisotropy and Apparent Diffusion Coefficient in Diffusion Tensor Imaging: Evaluation Using a Diffusional Anisotropic Phantom

Sang Joon Kim, MD, PhD1, Choong Gon Choi, MD, PhD1, Jeong Kon Kim, MD, PhD1, Sung-Cheol Yun, PhD2, Geon-Ho Jahng, PhD3, Ha-Kyu Jeong, PhD4, Eun Ju Kim, MA4

1Department of Radiology, Asan Medical Center, University of Ulsan College of Medicine, Seoul 138-736, Korea.

2Department of Biostatistics, University of Ulsan College of Medicine, Seoul 138-736, Korea.

3Department of Radiology, East-West Neomedical Center, Kyung Hee University College of Medicine, Seoul 134-727, Korea.

4Clinical Scientist, MR, Philips Healthcare, Seoul 140-200, Korea.

Corresponding author: Sang Joon Kim, MD, PhD, Department of Radiology, Asan Medical Center, University of Ulsan College of Medicine, 88 Olympic-ro 43-gil, Songpa-gu, Seoul 138-736, Korea. Tel: (822) 3010-3953, Fax: (822) 476-0090, sjkimjb@amc.seoul.kr

Received 24 March 2014       Accepted 26 December 2014

Copyright © 2015 The Korean Society of Radiology

(open-access):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Objective

To validate the usefulness of a diffusional anisotropic capillary array phantom and to investigate the effects of diffusion tensor imaging (DTI) parameter changes on diffusion fractional anisotropy (FA) and apparent diffusion coefficient (ADC) using the phantom.

Materials and Methods

Diffusion tensor imaging of a capillary array phantom was performed with imaging parameter changes, including voxel size, number of sensitivity encoding (SENSE) factor, echo time (TE), number of signal acquisitions, b-value, and number of diffusion gradient directions (NDGD), one-at-a-time in a stepwise-incremental fashion. We repeated the entire series of DTI scans thrice. The coefficients of variation (CoV) were evaluated for FA and ADC, and the correlation between each MR imaging parameter and the corresponding FA and ADC was evaluated using Spearman's correlation analysis.

Results

The capillary array phantom CoVs of FA and ADC were 7.1% and 2.4%, respectively. There were significant correlations between FA and SENSE factor, TE, b-value, and NDGD, as well as significant correlations between ADC and SENSE factor, TE, and b-value.

Conclusion

A capillary array phantom enables repeated measurements of FA and ADC. Both FA and ADC can vary when certain parameters are changed during diffusion experiments. We suggest that the capillary array phantom can be used for quality control in longitudinal or multicenter clinical studies.

Keywords: Diffusion tensor imaging, Fractional anisotropy, Apparent diffusion coefficient, Phantom study, Magnetic resonance imaging

INTRODUCTION

Diffusion tensor imaging (DTI) has been used as a quantitative imaging tool and is increasingly used to assess patients with various disorders of the central nervous system. Diffusion indices, such as fractional anisotropy (FA) and mean diffusivity (MD) or apparent diffusion coefficient (ADC), are often used to detect subtle changes in white matter that accompany various diseases (1), and have been demonstrated as useful biomarkers for pathological conditions or disease progression. However, measurement of diffusion indices can depend on various factors (2, 3, 4) including the MR scanner type, imaging parameters, patient factors such as age and gender, and inter- and intra-observer variations in the region-of-interest (ROI) analysis. In particular, the effect of changes in the imaging parameters seen on FA or ADC is still not completely understood. MR parameters such as the b-value, echo time (TE), the number of diffusion gradient directions (NDGD), and the number of signal acquisitions (NSA), reportedly influence the FA and ADC (5, 6, 7, 8, 9). However, most of these studies were performed on human subjects and with a limited scan environment, i.e., the number of adjustable imaging parameters, scan time, motion, number of subjects and reproducibility. Specifically, anatomical variations among the study subjects or difficulties in performing repeated examinations in the same individual may have lead to skewed results. The aforementioned disadvantages of human studies may be overcome using phantoms that allow multiple examinations, as well as the testing of various imaging parameters without limitation of time. Several types of anisotropic phantoms have been described in previously published studies (10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20). Organic materials, such as asparagus stems, have been tested, although these materials are neither controllable nor reproducible (10), and cannot be preserved over a long period of time. Other materials have included bundles of fibers, multiple acrylic plates, gel slices, arrays of channeled silicone plates, cylindrical containers filled with chemical materials, and capillary arrays (17). We used a capillary array phantom in the DTI experiment, and the effect of the changes in imaging parameters was investigated on FA and ADC using repeated measurements in the clinical MR imaging environment.

MATERIALS AND METHODS

Phantom Preparation

We intended to develop an anisotropic phantom that could then be used as a reference in clinical DTI studies of the human brain by attaching it to a patient's head. The phantom was constructed using a capillary array manufactured by Schott North America (Southbridge, MA, USA) and modified according to our specifications. The capillary array is made of lead silicate glass with a density of 3.0 g/cm3. The phantom specifications were a 10-mm diameter and a 10-mm length, filled with 50-µm diameter capillary pores occupying 50% of the cut surface area (Fig. 1A). For MR measurements, the phantom was placed in a test tube containing distilled water and then sealed. The water temperature was maintained by keeping the water container at room temperature for 1 hour before the experiment. Water was injected using a syringe into the array through a rubber tube connected to the outside of the array in order to eliminate air bubbles in the capillary array.
The phantom was attached to a bottle filled with 1000 mL of demineralized water mixed with 770 mg CuSO4.5H2O, 1 mL arquad, and 0.15 mL H2SO4 0.1 N solution to simulate the human brain examination. The phantom was attached to the water bottle and placed in the center of the head coil in order to avoid bias from any positional difference throughout the MR examination (Fig. 1B). This phantom setup was used throughout this study.

MR Examination

MR imaging of the phantom was performed using a 3.0-T MR scanner (Achieva, Philips Healthcare, Best, the Netherlands) with an 8 channel head coil. DTI was performed using the Stejskal-Tanner diffusion preparation with single shot spin-echo echo-planar imaging (21). The nominal 'delta', i.e., the time from the start of the first gradient to the start of the second gradient, and the 'delta', i.e., the duration of the gradient were 39 msec and 10 msec, respectively. These time parameters were used with a different diffusion gradient strength for each b-value throughout the experiments.
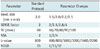
We used the standard DTI protocol with the following parameters: repetition time 6422 msec; TE 80 msec; field of view 224 mm; slice thickness 2 mm; 55 slices; b-value 0 and 800 sec/mm2; matrix 112 × 112; sensitivity encoding (SENSE) factor 2; NSA 2; and NDGD 15. Multiple DTI scans were performed with changing imaging parameters, i.e., voxel size, SENSE factors, TE, NSA, b-value, and NDGD one-at-a-time, and with each parameter changed in step wise increments. The parameters used were shown in Table 1. The entire series of DTI scans was repeated thrice, at one-week intervals, and with the same changes in parameters throughout the scans. In each series, 20 DTI scans were obtained and a total of 60 DTI scans were finally obtained.
We measured the signal-to-noise ratio (SNR) for each DTI scan. With parallel imaging in this experiment, conventional SNR measurement, which directly estimates the signal and the noise from the image foreground and background, respectively, could not be used due to the spatial variations of noise (g-factors). Instead, we separately obtained images with the excitation radiofrequency (RF) pulses turned off, and which resulted in a noise map with spatial aspects. The noise maps were obtained in each DTI scan by performing 2 dynamic scans, one with excitation RF pulses and the other without the RF pulses. The noise maps were obtained only in the first series of DTI scanning.

Post-Processing and Measurement of the Diffusion Tensor Indices

Diffusion tensor imaging results were transferred to an independent console, and FA and ADC maps were generated using a vendor-provided software program (FiberTrak software, Philips Healthcare, Best, the Netherlands) (Fig. 2). A 4-voxel ROI was placed at the center of the mid-portion slice in the phantom to measure the DTI indices, and the average FA and ADC values for the ROI were determined.
Pixel-wise ADC and FA maps were computed using the following equations:
ADC = (λ1 + λ2 + λ3) / 3
FA = √3/2 √([λ1 - λ]2 + [λ2 - λ]2 + [λ3 - λ]2) / (λ12 + λ22 + λ32)
where λ1, λ2, and λ3 are the 3 diffusion eigen values of the diffusion tensor and λ denotes the mean of the 3 eigen values. ADC is a measure of the average magnitude of the 3 eigen values, whereas FA represents the degree of diffusion anisotropy.

Measurement of SNR

The SNR was calculated using the following equation: SNR = mean of object / standard deviation (SD) of the noise in the object. As the SD of the noise in the object cannot be measured directly from the background signal when parallel imaging is used, the SD of the noise in the object was estimated from the mean of the noise image at the same location (22). Therefore, SNR = 1.253 × mean of object (ROI in the b0 [b-value = 0] image) / mean of the noise image (ROI in the noise image). The factor of 1.253 is a fixed factor relating the mean of the noise to the noise SD at the same location (23). ROIs of 100 mm2 were placed in the center of the fluid-filled bottle in the b0 image and in the corresponding noise image of each scan (Fig. 3).

Statistical Analysis

Variations in FA and ADC among the 3 repeated measurements were assessed by calculating the coefficient of variation (CoV) for FA and ADC in the protocol. For the calculation of the CoV, we first calculated the CoV in each parameter and then calculated the average value of the CoV, both for FA and ADC. The relationship between the imaging parameters and the DTI indices were evaluated using Spearman's correlation analysis. For each MR parameter, we combined all data from 3 estimates into a single series and performed Spearman's correlation analysis. All statistical analyses were performed using SPSS (version 18.0; SPSS Inc., Chicago, IL, USA).

RESULTS

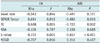
Using the standard protocol, the mean FA of the phantom was 0.229 (range 0.224-0.235, SD 0.0055) and the mean ADC was 1.742 × 10-3 mm2/s (range 1.687-1.824, SD 0.0726). The CoVs for FA and ADC for the capillary array phantom were 7.1% and 2.4%, respectively. There were significant positive correlations between the FA values and the SENSE factor (rho = 0.691, p = 0.013), TE (rho = 0.688, p = 0.005), and the b-value (rho = 0.701, p = 0.001), while the NDGD (rho = -0.767, p = 0.016) showed a significant negative correlation with the FA. There were significant negative correlations between the ADC and the SENSE factor (rho = -0.692, p = 0.013), TE (rho = -0.720, p = 0.002), and the b-value (rho = -0.837, p < 0.001), while there was no such correlation between the ADC and the NDGD (rho = 0.316, p = 0.407). The voxel size and the NSA did not correlate with either FA or ADC (Table 2). The SNR data were shown in the Supplementary Table 1 (in the online-only Data Supplement).

DISCUSSION

We used a capillary array phantom to investigate the effect of changes in DTI parameters on FA and ADC. We found that this phantom could be used as a reference for image quality in DTI images acquired in multicenter or longitudinal studies. Moreover, we found that both FA and ADC were significantly correlated with TE, the SENSE factors, and the b-values, and that FA was also significantly correlated with the NDGD.
Diffusion tensor imaging has been used in humans to investigate microstructural damage and white matter integrity. DTI can also be useful as a surrogate marker for many neurodegenerative or neoplastic diseases in the brain (1). However, its practical use is limited, by variations in the diffusion indices in different MR scanners, as well as by variations caused by the use of different imaging parameters, e.g., those used in longitudinal or multicenter trials (2, 3, 4). Therefore, it is necessary to develop a method that can assure the quality of DTI images acquired in multiple medical institutions. We considered that a phantom would be useful for validating DTI indices and for quality control of MR scanners and imaging parameters, as long as the phantom exhibits similar behavior for diffusion FA and ADC as in the human brain. A DTI phantom should be anisotropic and provide consistent values that are both stable and reproducible (14, 16, 17, 18). We utilized a capillary array phantom with modified design and dimensions to allow attachment to a patient's head in developing a phantom that can be used as a reference standard in clinical DTI studies of the human brain in multiple medical centers and over different time periods. We tested its feasibility for diffusion anisotropy measurements and found that its CoVs for FA and ADC were 7.1% and 2.4% respectively, which were considered acceptable for clinical use. We conducted a pilot test with the phantom attached to the head of a volunteer and obtained images with changing SENSE factors to ensure feasibility of the phantom in clinical studies. Both FA and ADC value variations in the volunteer test were similar to that of our experiment with the phantom attached to the water-filled bottle.
We used the capillary array phantom to test the effects of changes in the MR imaging parameters on FA and ADC. Of the many parameters that could be controlled in DTI (5, 6, 7, 8, 9), we selected those that could potentially affect DTI indices. The tested parameters were the b-value, TE, SENSE factor, NDGD, voxel size, and NSA.
Only a limited number of reports are available on the effects of MR parameter variations on the measurement of FA and ADC. Moreover, the results are inconsistent and some of the results differ from others. In the previous reports, FA showed no correlation with NSA (8) and a negative correlation with the voxel size and the NDGD (9, 24). Regarding SENSE factor, b-value and TE, some authors reported a positive correlation with FA (6, 25, 26) while others reported no correlation (3, 5). In the case of ADC, the b-value showed a negative correlation (5, 27, 28), while the SENSE factor or the NDGD showed no correlation (7, 24, 25). The correlation with TE differed according to the target area: no correlation with ADC in white matter (3, 6, 28), positive correlation in gray matter (29), and a negative correlation in cerebrospinal fluid (CSF) (28). There is no available report regarding the effect of variations in NSA or the voxel size on ADC.
The mechanism by which variations in imaging parameters causes changes in FA values is unclear, however, SNR seems to have an important role. It is well-known that the SNR depends on the imaging parameters and affects FA measurement. At moderate b-value ranges, FA is overestimated at a low SNR setting (30, 31). In contrast, the effect of the SNR on the ADC measurement is unclear and reports regarding the correlation between the ADC and the SNR are inconsistent in different studies (30).
In our experiment, FA showed positive correlation with the b-value, SENSE factor, and the TE and a negative correlation with the NDGD. There was no correlation between FA and NSA or the voxel size. Because FA is overestimated in a low SNR setting, conditions causing lower SNR will result in increased FA. With an increasing b-value, SENSE factor, or TE, the SNR is expected to decrease and, therefore, FA will be positively correlated with these parameters. A negative correlation of NDGD with FA can be similarly explained, i.e., increased NDGD will result in increased SNR and therefore, decreased FA. The reason for lack of correlation between the FA and the NSA or the voxel size is unclear. SNR increases with increasing NSA, and therefore, FA is expected to be decrease. However, in our experiment, the FA was not decreased with increasing NSA. There was no significant increase in the SNR with increasing NSA in the range of the NSA we tested, 1 to 4 in our preliminary experiment. Although we could not clearly identify the reason why the NSA change did not affect the FA, we speculated that the change in noise level did not differ significantly in our tested NSA range. Widjaja et al. (8) also reported that increasing NSA did not affect the FA in their human brain study, which was consistent with our results. Since we tested only a narrow range of variations in voxel size it likely resulted in no correlation between the FA and voxel size.
Apparent diffusion coefficient changes were more unpredictable, as compared to those of FA in our study. ADC showed a negative correlation with the b-value, SENSE factor and TE, and there was no correlation with the NSA, NDGD, or the voxel size. The negative correlation of ADC with the b-value is well-known in diffusion-weighted images, which was consistent with our results (5, 27, 28). The negative correlation of ADC with TE in our study corroborated previous studies using a gel phantom (32) or CSF (28) in humans. We speculated that the high range of the ADC values in our study explains our finding of a negative correlation of the ADC with the TE. Our result differed from those of a previous report that showed no correlation of the SENSE factor with the ADC (25). Although the reason is not yet clear, we speculate that the high ADC range in our study may explain this discrepancy. We detected no correlation between the NDGD and the ADC, similar to previous reports (7, 24).
Our experiment showed that FA and ADC may differ according to the MR imaging parameters. Moreover, the effect of individual MR parameters on FA or ADC was not consistent with that seen in previous studies that were not consistent, either. The reason for the inconsistency among studies is not clear. It can be attributed to the different range of implemented parameter values, different vendor machines or different field strength, different measurement location such as gray matter, white matter or CSF, as well as different subjects such as humans, animals, phantoms, or model simulation. The variations of FA and ADC value according to the MR imaging parameters may raise a problem in multicenter or longitudinal studies DTI data compatibility. Therefore, we suggest that implementing a phantom, as well as cautious selection of imaging parameters is warranted for quality assurance of DTI data in clinical studies.
Our study had several limitations. First, the FA and ADC values of our phantom were in a different range from that of normal white matter, which may have led to different effects on the FA and ADC than those observed in human brains. However, once reference FA and ADC ranges are set based on an in vivo DTI study, these values can be used in multiple medical institutions or research centers or in longitudinal studies, as a marker to ensure the minimum DTI image quality. A second limitation was the small size of our phantom. Although we intended to construct a small phantom to attach to a patient's head, this also causes susceptibility to image distortion and noise, which may have resulted in biases in the FA and ADC measured from the phantom. However, patient tolerance is also an important issue, and further studies will focus on the size of the phantom so that minimum image artifacts in the phantom, as well as patient comfort are ensured. Third, we only used one phantom in this study. Further studies with additional phantoms are needed in order to investigate their feasibility. Moreover, comparisons of phantoms and human brains are warranted to further verify the effects of MR parameter changes on the measurements of the FA and ADC values and to determine whether this technique can be successfully implemented as a tool for the quality assurance of DTI indices in MR scanners. Finally, the SNR measurement was not analyzed in our study because we only obtained the noise maps with the first series of our experiments in order to be used as a preliminary reference.
In conclusion, capillary array is an excellent choice for a diffusion anisotropy phantom, as it showed reasonable CoV in multiple FA and ADC value measurements. We found that the FA and ADC significantly correlated with the SENSE factors, TE, b-value, and the NDGD, although not with the voxel size or NSA. Attention to the choice of imaging parameters is important in applying DTI to clinical studies. We consider that the capillary array phantom can be used for quality control in longitudinal or multicenter clinical studies.

Figures and Tables

Fig. 1

Photographs of phantom and phantom installed in head coil.

A. Capillary array phantom, measuring 1 cm in length and 1 cm in diameter. B. Capillary array phantom (arrow) is attached to water-filled bottle and installed in 8-channel head coil. Phantom is securely placed in syringe tube filled with distilled water and air bubble is meticulously removed.
kjr-16-297-g001
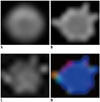Fig. 2

B0 (A), ADC (B), FA (C), and color-coded FA (D) images of phantom generated by post processing of DTI source images on workstation.

Water-filled bottle was cropped in figures. ADC = apparent diffusion coefficient, DTI = diffusion tensor imaging, FA = fractional anisotropy
kjr-16-297-g002
Fig. 3

SNR measurement.

Signal intensity was measured on b0 images of water-filled bottle (A). ROI of 100 mm3 was placed in center of bottle (arrow). Noise image was obtained simultaneously with DTI and noise was measured in corresponding area of b0 images (B, arrow). Noise image was used to measure noise, as it is very difficult to measure noise directly in images when using parallel imaging. SNR was calculated using following equation: SNR = 1.253 × mean of object (ROI in b0 image) / mean of noise image (ROI in noise image). Factor of 1.253 is fixed factor expressing mean of noise image to standard deviation of object with signal at same location. DTI = diffusion tensor imaging, ROI = region-of-interest, SNR = signal-to-noise ratio
kjr-16-297-g003
Table 1

Changes in MR Scan Parameters

kjr-16-297-i001
Parameter Standard Protocol Parameter Changes
Voxel size (mm × mm) 2.0 1.5/2.0/2.2/2.5
SENSE factor 2 2/2.5/2.8/4
TE (msec) 80 60/70/80/90/100
NSA 2 1/2/4
b-value 800 600/800/1000/1200/1600/2000
NDGD 15 6/15/32

Note.- NDGD = number of diffusion gradient directions, NSA = number of signals acquired, SENSE = sensitivity encoding, TE = echo time

Table 2

Correlations of MR Scan Parameters with FA and ADC

kjr-16-297-i002
FA ADC
Rho P Rho P
Voxel size -0.043 0.894 -0.497 0.101
SENSE factor 0.691 0.013 -0.692 0.013
TE 0.688 0.005 -0.720 0.002
NSA -0.105 0.787 0.158 0.685
b-value 0.701 0.001 -0.837 < 0.001
NDGD -0.767 0.016 0.316 0.407

Note.- ADC = apparent diffusion coefficient, FA = fractional anisotropy, NDGD = number of diffusion gradient directions, NSA = number of signals acquired, SENSE = sensitivity encoding, TE = echo time

Notes

This study was supported by a grant (2009-336) from the Asan Institute for Life Sciences, Seoul, Korea.

References

1. Dong Q, Welsh RC, Chenevert TL, Carlos RC, Maly-Sundgren P, Gomez-Hassan DM, et al. Clinical applications of diffusion tensor imaging. J Magn Reson Imaging. 2004; 19:6–18.
2. Landman BA, Farrell JA, Jones CK, Smith SA, Prince JL, Mori S. Effects of diffusion weighting schemes on the reproducibility of DTI-derived fractional anisotropy, mean diffusivity, and principal eigenvector measurements at 1.5 T. Neuroimage. 2007; 36:1123–1138.
3. Huisman TA, Loenneker T, Barta G, Bellemann ME, Hennig J, Fischer JE, et al. Quantitative diffusion tensor MR imaging of the brain: field strength related variance of apparent diffusion coefficient (ADC) and fractional anisotropy (FA) scalars. Eur Radiol. 2006; 16:1651–1658.
4. Zhu T, Hu R, Qiu X, Taylor M, Tso Y, Yiannoutsos C, et al. Quantification of accuracy and precision of multi-center DTI measurements: a diffusion phantom and human brain study. Neuroimage. 2011; 56:1398–1411.
5. Melhem ER, Itoh R, Jones L, Barker PB. Diffusion tensor MR imaging of the brain: effect of diffusion weighting on trace and anisotropy measurements. AJNR Am J Neuroradiol. 2000; 21:1813–1820.
6. Qin W, Yu CS, Zhang F, Du XY, Jiang H, Yan YX, et al. Effects of echo time on diffusion quantification of brain white matter at 1.5 T and 3.0 T. Magn Reson Med. 2009; 61:755–760.
7. Ni H, Kavcic V, Zhu T, Ekholm S, Zhong J. Effects of number of diffusion gradient directions on derived diffusion tensor imaging indices in human brain. AJNR Am J Neuroradiol. 2006; 27:1776–1781.
8. Widjaja E, Mahmoodabadi SZ, Rea D, Moineddin R, Vidarsson L, Nilsson D. Effects of gradient encoding and number of signal averages on fractional anisotropy and fiber density index in vivo at 1.5 tesla. Acta Radiol. 2009; 50:106–113.
9. Santarelli X, Garbin G, Ukmar M, Longo R. Dependence of the fractional anisotropy in cervical spine from the number of diffusion gradients, repeated acquisition and voxel size. Magn Reson Imaging. 2010; 28:70–76.
10. Boujraf S, Luypaert R, Eisendrath H, Osteaux M. Echo planar magnetic resonance imaging of anisotropic diffusion in asparagus stems. MAGMA. 2001; 13:82–90.
11. Chen B, Song AW. Diffusion tensor imaging fiber tracking with local tissue property sensitivity: phantom and in vivo validation. Magn Reson Imaging. 2008; 26:103–108.
12. Fieremans E, De Deene Y, Delputte S, Ozdemir MS, D'Asseler Y, Vlassenbroeck J, et al. Simulation and experimental verification of the diffusion in an anisotropic fiber phantom. J Magn Reson. 2008; 190:189–199.
13. Mattila S, Renvall V, Hiltunen J, Kirven D, Sepponen R, Hari R, et al. Phantom-based evaluation of geometric distortions in functional magnetic resonance and diffusion tensor imaging. Magn Reson Med. 2007; 57:754–763.
14. Sadleir RJ, Neralwala F, Te T, Tucker A. A controllably anisotropic conductivity or diffusion phantom constructed from isotropic layers. Ann Biomed Eng. 2009; 37:2522–2531.
15. Sakai K, Azuma T, Mori S. Rigid diffusion phantom: acquisition and simulation. Conf Proc IEEE Eng Med Biol Soc. 2008; 2008:451–453.
16. Watanabe M, Aoki S, Masutani Y, Abe O, Hayashi N, Masumoto T, et al. Flexible ex vivo phantoms for validation of diffusion tensor tractography on a clinical scanner. Radiat Med. 2006; 24:605–609.
17. Yanasak N, Allison J. Use of capillaries in the construction of an MRI phantom for the assessment of diffusion tensor imaging: demonstration of performance. Magn Reson Imaging. 2006; 24:1349–1361.
18. Poupon C, Rieul B, Kezele I, Perrin M, Poupon F, Mangin JF. New diffusion phantoms dedicated to the study and validation of high-angular-resolution diffusion imaging (HARDI) models. Magn Reson Med. 2008; 60:1276–1283.
19. Neher PF, Laun FB, Stieltjes B, Maier-Hein KH. Fiberfox: facilitating the creation of realistic white matter software phantoms. Magn Reson Med. 2014; 72:1460–1470.
20. Fillard P, Descoteaux M, Goh A, Gouttard S, Jeurissen B, Malcolm J, et al. Quantitative evaluation of 10 tractography algorithms on a realistic diffusion MR phantom. Neuroimage. 2011; 56:220–234.
21. Stejskal EO, Tanner JE. Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J Chem Phys. 1965; 42:288–292.
22. Li C, Chen W, Beatty P, Brau A, Hargreaves B, Busse R, et al. SNR quantification with phased-array coils and parallel imaging for 3D-FSE. In : Proceedings of the 18th Annual Meeting of ISMRM; Stockholm: 2010. (abstract 552).
23. Gudbjartsson H, Patz S. The Rician distribution of noisy MRI data. Magn Reson Med. 1995; 34:910–914.
24. Giannelli M, Cosottini M, Michelassi MC, Lazzarotti G, Belmonte G, Bartolozzi C, et al. Dependence of brain DTI maps of fractional anisotropy and mean diffusivity on the number of diffusion weighting directions. J Appl Clin Med Phys. 2009; 11:2927.
25. Alexander AL, Lee JE, Wu YC, Field AS. Comparison of diffusion tensor imaging measurements at 3.0 T versus 1.5 T with and without parallel imaging. Neuroimaging Clin N Am. 2006; 16:299–309. xi
26. Jones DK, Basser PJ. "Squashing peanuts and smashing pumpkins": how noise distorts diffusion-weighted MR data. Magn Reson Med. 2004; 52:979–993.
27. Bisdas S, Bohning DE, Besenski N, Nicholas JS, Rumboldt Z. Reproducibility, interrater agreement, and age-related changes of fractional anisotropy measures at 3 T in healthy subjects: effect of the applied b-value. AJNR Am J Neuroradiol. 2008; 29:1128–1133.
28. DeLano MC, Cooper TG, Siebert JE, Potchen MJ, Kuppusamy K. High-b-value diffusion-weighted MR imaging of adult brain: image contrast and apparent diffusion coefficient map features. AJNR Am J Neuroradiol. 2000; 21:1830–1836.
29. Vestergaard-Poulsen P, Hansen B, Ostergaard L, Jakobsen R. Microstructural changes in ischemic cortical gray matter predicted by a model of diffusion-weighted MRI. J Magn Reson Imaging. 2007; 26:529–540.
30. Farrell JA, Landman BA, Jones CK, Smith SA, Prince JL, van Zijl PC, et al. Effects of signal-to-noise ratio on the accuracy and reproducibility of diffusion tensor imaging-derived fractional anisotropy, mean diffusivity, and principal eigenvector measurements at 1.5 T. J Magn Reson Imaging. 2007; 26:756–767.
31. Zhan L, Leow AD, Jahanshad N, Chiang MC, Barysheva M, Lee AD, et al. How does angular resolution affect diffusion imaging measures? Neuroimage. 2010; 49:1357–1371.
32. Ogura A, Hayakawa K, Miyati T, Maeda F. Imaging parameter effects in apparent diffusion coefficient determination of magnetic resonance imaging. Eur J Radiol. 2011; 77:185–188.

Supplementary Material

The online-only Data Supplement is available with this article at http://dx.doi.org/10.3348/kjr.2015.16.2.297.

Supplementary Table 1

Changes in Signal-To-Noise Ratio According to MR Parameter Change
TOOLS
Similar articles