A Novel Nicotinamide Adenine Dinucleotide Correction Method for Mitochondrial Ca2+ Measurement with FURA-2-FF in Single Permeabilized Ventricular Myocytes of Rat

Jeong Hoon Lee; Jeong Mi Ha; Chae Hun Leem

doi:10.4196/kjpp.2015.19.4.373

Journal List > Korean J Physiol Pharmacol > v.19(4) > 1026039

Go to TopGo to Top Go to BottomGo to Bottom

TOOLS

Lee, Ha, and Leem: A Novel Nicotinamide Adenine Dinucleotide Correction Method for Mitochondrial Ca2+ Measurement with FURA-2-FF in Single Permeabilized Ventricular Myocytes of Rat

Original Article

The Korean Journal of Physiology & Pharmacology : Official Journal of the Korean Physiological Society and the Korean Society of Pharmacology 2015; 19(4): 373-382.

Published online: 30 June 2015

DOI: https://doi.org/10.4196/kjpp.2015.19.4.373

A Novel Nicotinamide Adenine Dinucleotide Correction Method for Mitochondrial Ca²⁺ Measurement with FURA-2-FF in Single Permeabilized Ventricular Myocytes of Rat

Jeong Hoon Lee, Jeong Mi Ha, Chae Hun Leem

Department of Physiology, University of Ulsan College of Medicine/Asan Medical Center, Seoul 138-736, Korea.

Corresponding to: Chae Hun Leem, Department of Physiology, University of Ulsan College of Medicine/Asan Medical Center, 88 43-gil, Olimpic-ro, Songpa-gu, Seoul 138-736, Korea. (Tel) 82-2-3010-4287, (Fax) 82-2-3010-8151, leemch@gmail.com, leemch@amc.seoul.kr

Received 25 March 2015 Revised 31 March 2015 Accepted 2 April 2015

(open-access, http://creativecommons.org/licenses/by-nc/4.0/):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Fura-2 analogs are ratiometric fluoroprobes that are widely used for the quantitative measurement of [Ca²⁺]. However, the dye usage is intrinsically limited, as the dyes require ultraviolet (UV) excitation, which can also generate great interference, mainly from nicotinamide adenine dinucleotide (NADH) autofluorescence. Specifically, this limitation causes serious problems for the quantitative measurement of mitochondrial [Ca²⁺], as no available ratiometric dyes are excited in the visible range. Thus, NADH interference cannot be avoided during quantitative measurement of [Ca²⁺] because the majority of NADH is located in the mitochondria. The emission intensity ratio of two different excitation wavelengths must be constant when the fluorescent dye concentration is the same. In accordance with this principle, we developed a novel online method that corrected NADH and Fura-2-FF interference. We simultaneously measured multiple parameters, including NADH, [Ca²⁺], and pH/mitochondrial membrane potential; Fura-2-FF for mitochondrial [Ca²⁺] and TMRE for Ψ_m or carboxy-SNARF-1 for pH were used. With this novel method, we found that the resting mitochondrial [Ca²⁺] concentration was 1.03 µM. This 1 µM cytosolic Ca²⁺ could theoretically increase to more than 100 mM in mitochondria. However, the mitochondrial [Ca²⁺] increase was limited to ~30 µM in the presence of 1 µM cytosolic Ca²⁺. Our method solved the problem of NADH signal contamination during the use of Fura-2 analogs, and therefore the method may be useful when NADH interference is expected.

Keywords: Calcium, Fura-2-FF, Mitochondrial membrane potential, NADH, pH

ABBREVIATIONS

acetoxymethylester

ADP

adenosine diphosphate

ATP

adenosine triphosphate

Carboxy-SNARF-1-AM

carboxy-seminaphtorhodafluor-1-acetoxymethylester

CCD

charge-coupled device

CPX

Ca²⁺-H⁺ exchanger

EGTA

ethylene glycol-bis(2-aminoethylether)-N,N,N',N'-tetraacetic acid

FCCP

Carbonyl cyanide-p-trifluoromethoxyphenylhydrazone

HEPES

N-2-hydroxyethylpiperazine-N'-2-ethanesulfonic acid

K_d

dissociation constant

mCU

mitochondrial Ca²⁺ uniporter

mNCX

mitochondrial Na⁺-Ca²⁺ exchanger

MPTP

mitochondrial permeability transition pore

NADH

Nicotinamide adenine dinucleotide

PMTs

photomultiplier tubes

RaM

rapid mode of Ca²⁺ uptake

RyR

ryanodine receptor channel

S.E.

Standard error

sarcoplasmic reticular

TMRE

Tetramethylrhodamine ethyl ester

Ψ_m

mitochondrial membrane potential

INTRODUCTION

Ca²⁺ is an essential element involved in initiating and controlling the excitation-contraction coupling process in cardiac myocytes. The predominant Ca²⁺ source is trans-sarcolemmal Ca²⁺ influx and SR Ca²⁺ release [1 2 3]. For many years, mitochondria were simply regarded as an ATP-generating factory. However, several recent reports showed that mitochondria participate in many other important processes, such as apoptosis, ischemic-reperfusion injury, aging, and other diseases [4 5 6 7 8]. All of those phenomena are related to Ca²⁺ [4 5 6 7 8].

Several mechanisms of mitochondrial Ca²⁺ regulation in cardiac myocytes were reported, including involvement of the mCU [4 6 7 9], RaM [10 11], the RyR [12 13], the mNCX [14 15 16 17], and the CPX [18 19]. To date, their dynamics and quantitative roles in cardiac myocyte mitochondrial Ca²⁺ regulation were unclear. Further, their exact working mechanism, molecular identity, and regulatory factors were unknown. The role of mitochondria in cytosolic Ca²⁺ regulation in cardiac myocytes was controversial as well [4 6 7 9 20]. In order to study these issues, quantitative and real-time measurements of [Ca²⁺]_m were required.

The [Ca²⁺]_m range was reportedly 0.08 to 20 µM [21 22 23 24]. The most frequently used fluoroprobe to determine this range was rhod-2. Rhod-2-AM has a positive charge, and therefore it may preferentially load into mitochondria because of the large negative potential of the mitochondrial matrix. However, rhod-2 has limitations regarding quantitative mitochondrial Ca²⁺ measurement because it is not a ratiometric dye. In addition, rhod-2 can measure only up to several µM of Ca²⁺ because its dissociation constant (K_d) ranged from 0.57 to 0.80 µM [12 25 26].

Fura-2 analogs are widely used for quantitative measurements of [Ca²⁺]. The K_d value of Fura-2-FF was reportedly 18~35 µM in calibrating buffers [27 28 29 30 31] and 6~13 µM in cells [27 32]. However, this dye has potential usage problems due to NADH contamination and dye loading into mitochondria. Specifically, NADH contamination is a serious problem because most NADH is located in the mitochondria and because [NADH] change is related to mitochondrial membrane potential (Ψ_m), in turn, [Ca²⁺]_m change [33 34 35 36]. These problems have been ignored and no methods exist to avoid or overcome them.

In this report, we developed a novel online NADH correction method to measure [Ca²⁺]_m quantitatively, as well as a method to simultaneously measure multiple parameters, including NADH, [Ca²⁺]_m, and pH/Ψ_m.

METHODS

Cell preparation

Sprague-Dawley (SD) rats (8~10 weeks old) were anesthetized with a mixture of ketamine hydrochloride (90 mg/kg) and Rompun® (10 mg/kg). We injected the anesthetics intraperitoneally. The rat chest cavity was opened, and the heart was excised and mounted on a Langendorff-type apparatus. The heart was sufficiently perfused with Tyrode's solution (mmol/L: NaCl, 133.5; KCl, 5.4; HEPES, 5; taurine, 20; MgCl₂, 3; CaCl₂, 0.75; and glucose, 5.5; pH adjusted to 7.4 with NaOH) to remove all residual blood in the heart. Subsequently, the heart was perfused with Ca²⁺-free Tyrode's solution (mmol/L: NaCl, 133.5; KCl, 5.4; HEPES, 5; taurine, 20; MgCl₂ 3; EGTA 0.5; glucose, 5.5; pH adjusted to 7.4 with NaOH), and then with collagenase (Worthington Biochemical Co., NJ, USA) containing Tyrode's solution (mmol/L: NaCl, 133.5; KCl, 5.4; HEPES, 5; taurine, 20; MgCl₂, 3; CaCl₂, 0.15; and glucose, 5.5; collagenase, 0.8 mg/mL; pronase, 0.04 mg/mL; pH adjusted to 7.4 with NaOH) for 15 minutes. Single cardiac myocytes were dispersed by gentle agitation of the digested heart in a high K⁺-low Cl^- solution and stored in cell culture medium (Dulbecco's modified Eagle's medium; Sigma, St. Louis, USA) at room temperature (24~26℃) for later use. The high K⁺-low Cl^- solution was comprised of the following, in mmol/L: KCl, 25; K-glutamate, 70; KH₂PO4, 10; taurine, 10; glucose, 11; EGTA, 0.5; and HEPES, 10; pH adjusted to 7.2 with KOH. All experimental protocols were approved by our institutional animal care and use committee.

Solutions and reagents

Fura-2-FF was purchased from TEFLabs (TX, USA). The TMRE and carboxy-SNARF-1-AM were obtained from Invitrogen (Seoul, Korea).

Fluoroprobe loading procedure

Ventricular myocytes were incubated in Fura-2-FF-AM (8 µM) solution for 60 min at 4℃, and then at 37℃ for 30 min. Next, ventricular myocytes were incubated for 60 min at 37℃ with a dye-free solution to sufficiently hydrolyze the AM ester dye. Finally, the ventricular myocytes were transferred into and incubated in fresh medium. If carboxy-SNARF-1 was needed for the study, the dye (2 µM) was added into the second incubation step. To remove cytosolic compartments and to visualize the mitochondrial fluorescence, single isolated cardiomyocytes were perfused with saponin (0.1 mg/mL) for 60 s in the perfusing bath which is mounted on the inverted microscope (Fig. 1). All experiments were performed at 37℃.

Spectrofluorometric measurements with a multiparametric measurement system

A fast monochromator (Polychrome II; Till Photonics, Inc., Germany) was used as an excitation light source. A fused quartz light guide was used to divert the excitation light to an inverted microscope (TE-300; Nikon, Tokyo, Japan). An oil immersion lens (40x, NA 1.3) was used. A near infrared filter (Chroma Technology Corp., Bellows Falls, VT, USA) was used between the microscope illuminator and specimen to monitor the object field with a charge-coupled device (CCD) camera (FTM1800NH/HGI; Philips, Salt Lake, USA). The image was captured with a BT878-based TV capture board, and the object field or cell area, as a pixel unit, was measured with custom-made software. The object field area was set with a field diaphragm (Nikon, Tokyo, Japan). Four photomultiplier tubes (PMTs) were used to detect emission wavelengths, and each had band-pass filters (450, 500, 590, and 640 nm). Dichroic mirrors and band-pass filters were purchased from Chroma (Brattleboro VT, USA). A photon counting method was applied with the combination of a photomultiplier tube (R2949; Hamamatsu, Hamamatsu Japan), photon counter unit (C3866; Hamamatsu, Hamamatsu, Japan), and high-speed counter (NI 6602; National Instruments, Austin, USA). Custom-made driving software was used to control and sample data. A diagram of the whole system is shown in Fig. 1.

RESULTS

Development of a NADH correction method

NADH-Fura-2 signal interference

Simultaneous measurement of Fura-2-FF and NADH was technically difficult because each fluoroprobe produced signal interference. Fig. 2 shows this interference. Emission wavelengths of 450 and 500 nm were selected for NADH and Fura-2-FF, respectively. The excitation spectrums of both fluoroprobes overlapped. In addition, each fluoroprobe could generate emission at both 450 and 500 nm. The light intensity at each emission, therefore, contained signals from both fluoroprobes. This interference had to be corrected to obtain an exact measurement of the emission signal, specifically the quantitative measurement of Ca²⁺ with Fura-2-FF.

Correction principles

The excitation wavelength and the concentration of NADH can affect the emission intensity but not the emission spectral curve. Changes in [Ca²⁺] did not affect the emission and excitation spectrums of NADH (data not shown). Thus, the 450 and 500 nm ratio of NADH was constant at any excitation wavelength. The same principle can be applied to Fura-2-FF if NADH or [Ca²⁺] does not affect the emission and excitation spectrums of Fura-2-FF. However, the Fura-2-FF emission spectrum was shifted to the left by Ca²⁺ (Fig. 3B). Therefore, only isosbestic excitation could generate a Ca²⁺-independent emission spectrum. The isosbestic point was different for each emission wavelength (i.e., 450 and 500 nm). To minimize NADH contamination during isosbestic point acquisition, 10 µM FCCP and 10 µM ADP were added in the absence of mitochondrial substrates. The residual emission intensity was measured, and the relationship between the intensity and the cell area was obtained for correction of subsequent experiments. After myocytes were loaded with Fura-2-FF, the cell area was measured in each cardiac myocyte to correct the residual signals. The excitation spectrums at 450 and 500 nm emission were obtained by changing [Ca²⁺] from 0 to 10 mM under FCCP-free and mitochondrial substrate-free conditions (Fig. 4A and B). The excitation spectrum of the Ca²⁺-bound state was subtracted from the excitation spectrum of Ca²⁺-free conditions. Those subtracted curves are shown in Fig. 4C and D. To obtain an isosbestic point, we chose the wavelength showing the minimum standard deviation value (Fig. 4E and F). The isosbestic points were 361 at 450-nm emissions and 353 at 500-nm emissions, respectively. Using isosbestic excitation, the following equations were valid:

(1)

F_361,450=F_361,450,NADH+F_361,450,fura

(2)

F_353,500=F_353,500,NADH+F_353,500,fura

(3)

F_400,500=F_400,500,NADH+F_400,500,fura

where F_x,y is the measured emission intensity at y nm by x nm excitation, F_x,y,NADH represents the pure NADH-dependent emission intensity, and F_x,y,fura represents the pure Fura-2-FF dependent emission intensity. In addition, the R_f, R_N1, and R_N2 values must be constant because of the consistent shape of the emission spectrum:

(4)

R_f=F_361,450,fura/F_353,500,fura

(5)

R_N1=F_400,500,NADH/F_361,450,NADH

(6)

R_N2=F_353,500,NADH/F_361,450,NADH

With these constants, equations (1), (2), and (3) can be changed as follows:

(7)

F_361,450=F_361,450,NADH+R_f^*F_353,500,fura

(8)

F_353,500=R_N2^*F_361,450,NADH+F_353,500,fura

(9)

F_400,500=R_N1^*F_361,450,NADH+F_400,500,fura

If the constants, R_f, R_N1, and R_N2, were known, the pure NADH and Fura-2-FF signals could be obtained by solving the above equations. The R_f was calculated with the fluorescence intensity observed in Fig. 4A and B. R_N1 and R_N2 were obtained in myocytes that were not loaded with Fura-2-FF. The NADH signal was changed according to the supply of mitochondrial substrates: malate, pyruvate, or malate plus pyruvate (Fig. 5A and B). The linear relationships of F_400,500,NADH vs. F_361,450,NADH and F_353,500,NADH vs. F_361,450,NADH are shown in Fig. 5C, and each slope indicates R_N1 and R_N2. The equations of each pure signal values are as follows:

(10)

F_361,450,NADH=(A-R_f^*B)/(1-R_f^*R_N2)

(11)

F_{353,500, fura} / F_{400,500, fura} = R_{fura} = (\frac{R_{N_{2}} * A - B}{R_{N_{2}} * R_{f} - 1}) / (C - R_{N_{1}} \frac{A - R_{f} * B}{1 - R_{f} * R_{N_{2}}})

R_fura is the ratio value of Fura-2-FF that was used to calculate the free calcium concentration.

Background subtraction

The excitation light intensity used to induce fluorescence was much stronger than the fluorescence emission. Although the selected excitation wavelength was far different from the emission wavelength and was blocked using a band-pass filter, the stray light from excitation was still present. The stray light was reflected at the boundary between the solution and the cover slip and diffracted in the cells due to cellular components. Cells may also produce unwanted autofluorescence. Those signal artifacts were comparable to the real fluorescence emission from the dye; thus, correction was necessary. First, the reflected signal at the cover slip boundary was measured. Then, the background signal due to cellular autofluorescence was measured in the presence of FCCP and in the absence of mitochondrial substrates. The cell-dependent background signal was linearly related to the cell area; these relationships are shown in Fig. 6. Later, the dye-loaded cellular area was measured, and the autofluorescence calculated from the cellular area was corrected. Further, the cell-free window background was also measured and subtracted. The background correction was performed before the experiments began. We determined the relationship between the cellular area and cellular autofluorescence on each experimental day.

Calibration equation

The Ca²⁺ concentration could be calculated from the ratio value calculated from equation (11) using Grykiewicz's equation [37]. To convert the ratio into a concentration, the equation required four parameters: K_d, dissociation constant; R_min, minimum ratio; R_max, maximum ratio; and F_380,max/F_380,min, the ratio of maximum and minimum at 380 nm excitation. However, applying the equation was not easy because both R_max and F_380,max/F_380,min require Ca²⁺-saturated conditions without dye-loss. Replicating that condition in real cells was a difficult and erroneous procedure. In mitochondria, dye-saturated conditions for Fura-2-FF without dye-loss were virtually impossible. We found that the Ca²⁺-bound form of Fura-2-FF was practically non-fluorescent at 400-nm excitation. The new equation using this property was developed and is as follows:

(12)

[Ca²⁺] =K_d·(F_400,500,max/F_353,500,max)·(R-R_min)

The F_400,500,max and F_353,500,max are maximum values of the emitted signals at 500 nm with the excitation at 400 and 353 nm. Since F_353,500,max was an isosbestic emission value and was constant, the above equation could be simplified further as follows:

(13)

[Ca²⁺]=K_d·(1/R_min)·(R-R_min)

The details of the derivation of the above equations are shown in the Appendix.

The K_d of Fura-2-FF

To apply the calibration equation, the K_d value had to be determined. If we knew the free [Ca²⁺] and the other parameters in the calibration equation, we could calculate K_d. To calculate the free Ca²⁺ concentration, WINMAXC32 version 2.50 (Chris Patton, Stanford University) was used. EGTA purity was double-checked using the pH and oxalate method [38 39 40 41 42]. We obtained pH-dependent changes of K_d values in a cell-free solution. To simulate the experimental conditions, we measured pH-dependent K_d values with a dye-free cell in the window. A summary of the measured K_d values is shown in Table 1.

Mitochondrial pH changes by the change in [Ca²⁺]_m

Using carboxy-SNARF loaded myocytes, mitochondrial pH changes were determined following Ca²⁺ changes (Fig. 7). The increase in [Ca²⁺]_m did not affect mitochondrial pH. The mitochondrial pH was 7.504±0.047 (mean±standard error [S.E.], n=13). The K_d value of Fura-2-FF at pH 7.5 was 5.28 µM; this value was used for later Ca²⁺ calculations.

Mitochondrial Ca²⁺ changes due to correction

Fig. 8 shows the differences in Ca²⁺ concentrations before and after the correction. The results clearly showed the importance of correction for NADH and Fura-2-FF interference. The mitochondrial resting calcium concentration was 1.03±0.13 µM (mean±S.E., n=32) and the maximum [Ca²⁺]_m at 1 µM cytosolic Ca²⁺ ([Ca²⁺]_c) was 29.6±1.61 µM (mean±S.E., n=33) (Fig. 9).

Simultaneous measurement of NADH, [Ca²⁺]_m, and Ψ_m

TMRE has a positive charge and is distributed in a membrane potential-dependent manner. If the concentration in each compartment is known, the membrane potential can be calculated using Nernst's equation. TMRE was perfused at 2 nM to record the changes in the TMRE signal in mitochondria. The resting Ψ_m was assumed to be -150 mV. Based on this, Ψ_m was calculated. NADH was decreased by the application of Ca²⁺, but the Ψ_m remained similar (Fig. 10).

DISCUSSION

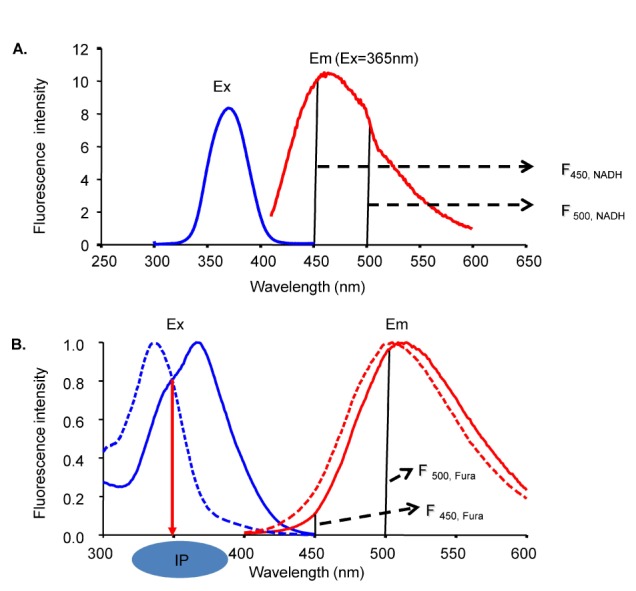
Interest in the ubiquitous role of Ca²⁺ in cells and cellular organelles is increasing. To study Ca²⁺ dynamics, the use of Ca²⁺ indicators has steadily increased. Mitochondria have now become a focus because of their role in many cellular processes, such as energy generation, apoptosis, ischemic-reperfusion injury in the heart, aging, etc. Ca²⁺ has a central role in these processes. However, quantitative and dynamic mitochondrial Ca²⁺ data are not yet available. For quantitative measurement of mitochondrial Ca²⁺, a ratiometric approach is essential. Ratiometric fluoroprobes are advantageous for quantitative measurement of [Ca²⁺] because dye loss due to leakage or photobleaching does not affect the calculation of [Ca²⁺]. These problems cannot be avoided when single excitation and single emission dyes are used to determine [Ca²⁺].

Fura-2 was first introduced in 1985 as a ratiometric fluorescent dye [37]; several analogs were subsequently developed. However, Fura-2 has several disadvantages when used to measure mitochondrial Ca²⁺. First, targeted dye loading into the mitochondria is not easy. Therefore, Fura-2 would likely be nonspecifically loaded into all organelles of the cell. One major Ca²⁺-related organelle is the SR. However, the total SR and mitochondria percent volumes are about 3.5% and 34~36%, respectively, in rat ventricular myocytes [43 44]. Therefore, even though Ca²⁺ in SR may affect the results, the effect would be negligible. Second, cellular autofluorescence from NADH could contaminate the Fura-2 signal. More than 90% of cellular NADH is present in the mitochondria (data not shown). Excitation and emission spectrums of NADH and Fura-2 widely overlap. Importantly, Ca²⁺ changes in mitochondria could affect NADH, which, in turn, affects Fura-2 signals. Therefore, this complicated interference must be solved to quantitatively measure [Ca²⁺]_m. This problem, however, has not been systematically investigated since Fura-2 was introduced. We were able to successfully correct for the interference between NADH and Fura-2 using the spectral characteristics of NADH and Fura-2. 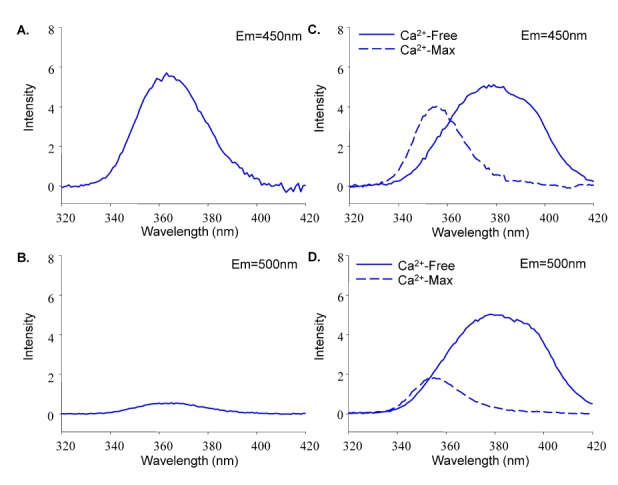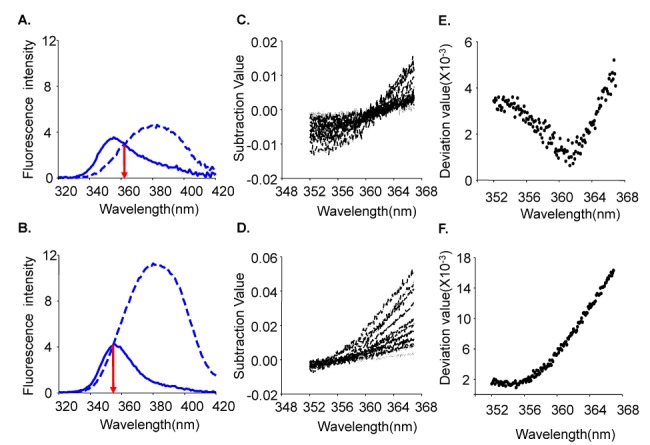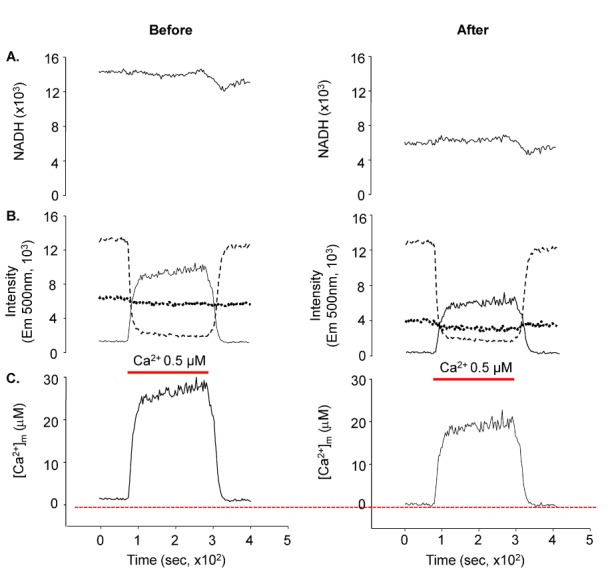Fig. 8 shows the effect of NADH and Fura-2-FF interference. The NADH signal was considerably decreased after the correction (Fig. 8). The corrected Fura-2-FF signal resulted in lower [Ca²⁺]_m. This interference implied that data from previous reports using Fura-2 analogs could be wrong, as the NADH signal could be different based on the correction or lack thereof. We would like to further investigate this possibility in the future.

Our calibration equation (Equation 12) has many advantages over Grynkiewicz's equation. First, it only required three calibration parameters: K_d, F_340,max/F_400,max, and R_min. Second, the ratio value was directly linear to the Ca²⁺ concentration at a constant pH. Therefore, the rate of ratio change could be directly converted to the rate of Ca²⁺ change. Third, obtaining the calibration parameters, particularly F_340,max/F_400,max, is relatively error-free. In Grynkiewicz's equation, F_380,max/F_380,min is prone to error because it divides the largest number by the smallest number. In addition, to obtain F_380,max/F_380,min, we had to accomplish real free- and saturated-[Ca²⁺] conditions because F₃₈₀ must reach the real maximum and minimum values, respectively. If not, F_380,max/F_380,min can easily be faulty. However, in our new equation, the F_340,max/F_400,max measurement error is much smaller because it is the ratio of the largest numbers at each excitation. Fourth, as shown in Equation 13, when the isosbestic excitation value was chosen instead of 340 nm in the new equation, only R_min is required to convert the ratio into the Ca²⁺ concentration if the pH was unchanged and the K_d value at that pH is known. Finally, the calibration procedure is much simpler, as R_min is the only parameter needed.

However, there are limitations associated with use of the equation. The new equation was generated based on the assumption that the emission of Ca²⁺-saturated Fura-2-FF was zero at 400-nm excitation. However, Ca²⁺-saturated Fura-2-FF actually produces a small emission. This causes deflection from the linearity between the ratio and Ca²⁺ concentration at very high Ca²⁺ concentrations. We that found our equation could be reasonably applied to [Ca²⁺]_m concentrations up to 50-fold that of the K_d. This range is reasonably acceptable under experimental conditions. The new equation still does not solve the problems of incomplete hydrolysis of the AM form of the dye, dye compartmentalization, autofluorescence, etc. Dye loading problems are inevitable, but careful loading and washing may minimize these kinds of errors (see Ref. [45]). In the case of compartmentalization, mitochondria had the largest volume; therefore, this type of error could be ignored. We used a very careful loading procedure to minimize incomplete hydrolysis of the AM form; therefore, we believe that this error was also minimized.

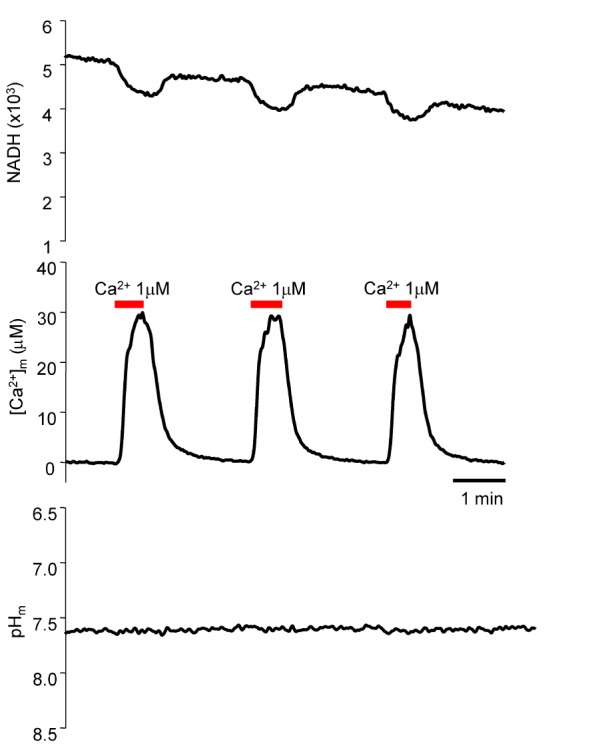
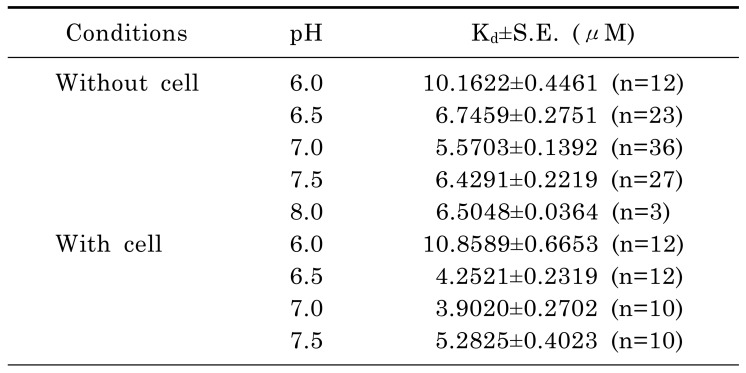
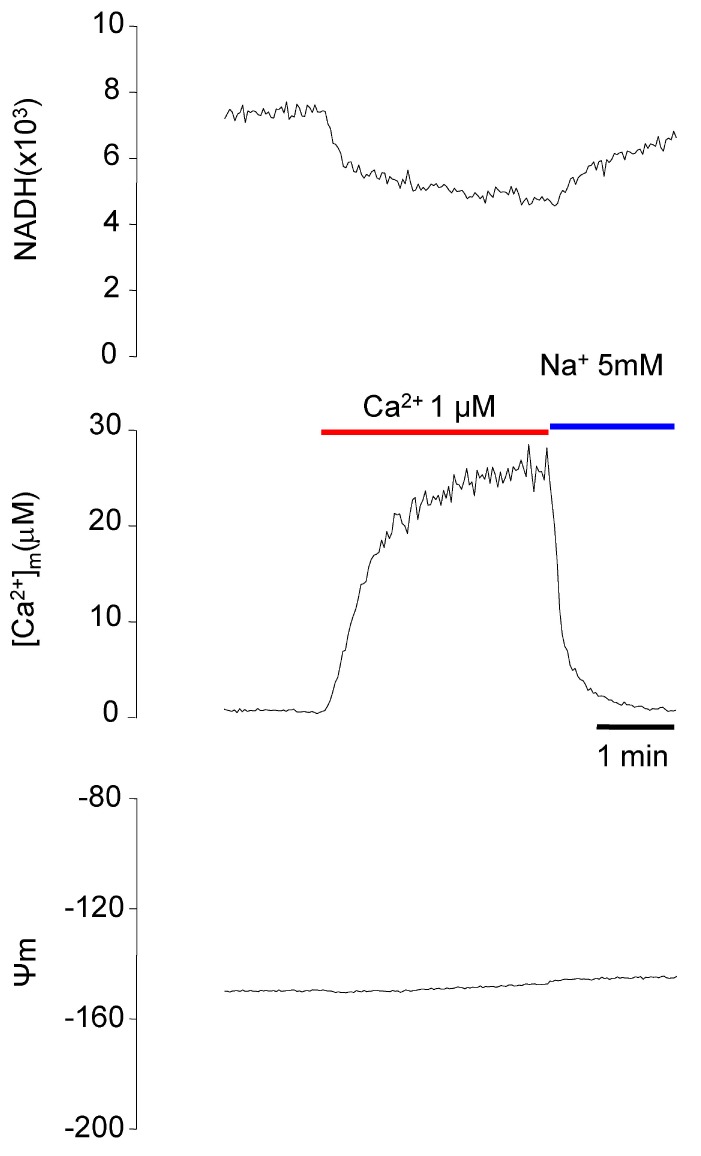
The K_d value of Fura-2-FF is pH dependent; therefore, if the procedure could cause changes in pH, we need to consider the pH effect when calculating [Ca²⁺]_m. Cytosolic Ca²⁺ application increased [Ca²⁺]_m, but the mitochondrial pH did not change. Therefore, the constant K_d at pH 7.5 was used to calculate [Ca²⁺]_m.

Our microfluorometry system could measure NADH, [Ca²⁺]_m, and pH_m simultaneously. In addition, the Ψ_m could be measured using TMRE because the excitation and the emission spectrum of TMRE overlapped with those of carboxy-SNARF-1. Therefore, we were able to successfully measure Ψ_m using TMRE (Fig. 10).

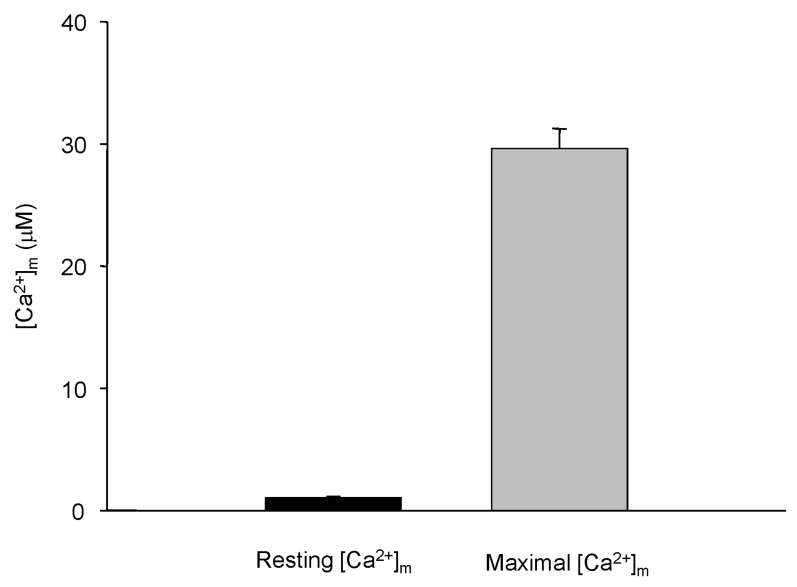
The resting [Ca²⁺]_m was approximately 1.03 µM. A previous report showed that [Ca²⁺]_m ranged from 0.08 to 0.17 µM [23 24]. Our study revealed a higher value than that of previous reports (see Refs. [23 24]). The change in [Ca²⁺]_m plays a central role in the exercise-dependent increase in ATP by activating three mitochondrial matrix Ca²⁺-sensitive enzymes (pyruvate dehydrogenase, α-ketoglutarate dehydrogenase, and NAD-dependent isocitrate dehydrogenase) [46 47 48 49 50 51]. Pyruvate and α-ketoglutarate dehydrogenase were almost fully activated at 1 µM because of the low K_d values, 0.77 and 0.28 µM, respectively [51]. The K_d value of NAD-dependent isocitrate dehydrogenase was 5.4 µM [51]. Therefore, the [Ca²⁺]_m-dependent increase in ATP may be due to the activation of NAD-dependent isocitrate dehydrogenase.

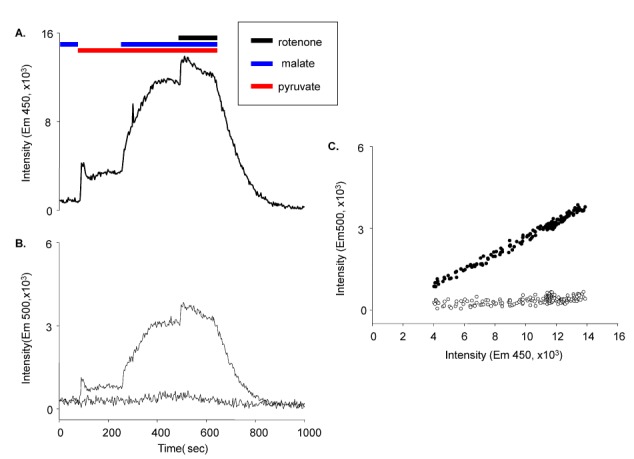
The maximal attainable [Ca²⁺]_m seemed to be limited. Our data showed that the maximal [Ca²⁺]_m was about 30 µM at 1 µM cytosolic Ca²⁺. Even when we applied more than 1 µM, the maximal [Ca²⁺]_m was not increased further (data not shown). The 30 µM concentration is far below the electrochemical equilibrium because the Ψ_m is about -150 mV and the concentration of the electrochemical equilibrium must be up to 10⁵ times the cytosolic [Ca²⁺]. This limitation implied the strong possibility that other mechanisms exist to limit Ca²⁺ increase in mitochondria. This may be a Ca²⁺ efflux mechanism, an inhibitory regulator of Ca²⁺ influx, or the increase in Ca²⁺ buffer by a volume increase or an actual buffer increase. Until now, two mechanisms were suggested for mitochondrial Ca²⁺ efflux, mNCX and CPX. Ca²⁺ was applied under 0 mM Na⁺ conditions; therefore, mNCX could not be the efflux mechanism involved in limiting the increase in [Ca²⁺]_m. CPX may change mitochondrial pH because it causes influx of H⁺ into mitochondria. However, mitochondrial pH was not changed during [Ca²⁺]_m increase. The MCU, a major Ca²⁺ influx pathway, did not show inactivation [52]. The electrochemical gradient for Ca²⁺ influx was huge, and thus it would likely be difficult for CPX to counteract the Ca²⁺ influx to limit the [Ca²⁺]_m increase. Another possibility is the opening of the MPTP. It was reported that [Ca²⁺]_m overload could open the MPTP [53 54 55]. However, MPTP is permeable to 1.5-kDa molecules [54 55 56]; if the MPTP was opened, Fura-2-FF or NADH would be decreased. Further, if the MPTP was opened, the Ψ_m would be substantially depolarized. However, we did not observe these phenomena. Mitochondria are known to be a Ca²⁺ sink because of their relatively larger Ca²⁺ buffering capacity [57 58 59 60]. If the limitation was caused by the buffer, [Ca²⁺]_m must continuously increase, even though the speed was slower; however, this was not observed. Ca²⁺ and Pi could form a precipitate [61], and free [Ca²⁺]_m may not increase because of continuous precipitate formation. Another possibility is mitochondrial swelling. Ca²⁺ overload caused mitochondrial swelling, an indication of MPTP opening [53 54 55]. However, actual swelling may occur without MPTP opening. Mitochondria reportedly had a Pi-containing particle [61]. Mitochondrial swelling and dissolution of those particles may increase mitochondrial buffering capacity to limit [Ca²⁺]_m increase. The Pi effect on mitochondrial Ca²⁺ dynamics requires further study.

In conclusion, we successfully developed a method to solve NADH and Fura-2-FF interference. This method enables more accurate Ca²⁺ measurements. In particular, quantitative measurement of mitochondrial Ca²⁺ dynamics is now possible and many uncertainties surrounding mitochondrial Ca²⁺ dynamics can be answered in the future using our new method.

ACKNOWLEDGEMENTS

This research was partly supported by the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (No. 2011-0010965) and (No. 2012-0009829).

ABBREVIATIONS

acetoxymethylester

ADP

adenosine diphosphate

ATP

adenosine triphosphate

Carboxy-SNARF-1-AM

carboxy-seminaphtorhodafluor-1-acetoxymethylester

CCD

charge-coupled device

CPX

Ca²⁺-H⁺ exchanger

EGTA

ethylene glycol-bis(2-aminoethylether)-N,N,N',N'-tetraacetic acid

FCCP

Carbonyl cyanide-p-trifluoromethoxyphenylhydrazone

HEPES

N-2-hydroxyethylpiperazine-N'-2-ethanesulfonic acid

K_d

dissociation constant

mCU

mitochondrial Ca²⁺ uniporter

mNCX

mitochondrial Na⁺-Ca²⁺ exchanger

MPTP

mitochondrial permeability transition pore

NADH

Nicotinamide adenine dinucleotide

PMTs

photomultiplier tubes

RaM

rapid mode of Ca²⁺ uptake

RyR

ryanodine receptor channel

S.E.

Standard error

sarcoplasmic reticular

TMRE

Tetramethylrhodamine ethyl ester

Ψ_m

mitochondrial membrane potential

Appendix

Derivation of the new calibration equations

If the fluorescent dye is only bound to Ca²⁺, the following equation is valid:

(1a)

[{Ca}^{2 +}] = K_{d} \frac{D_{b}}{D_{f}}

Total dye concentration: D_T

Free-form dye concentration: D_f

Ca²⁺-bound-form dye concentration: D_b

Dissociation constant: K_d.

If each form of the dye generates fluorescence emission at k by the excitation wavelengths x and y, the fluorescence intensity of the mixture of the free- and bound-form dye is as follows:

(2a)

F_x,k=a·D_f+b·D_b

(3a)

F_y,k=c·D_f+d·D_b

where F_x,k is the emitted intensity at k by the x excitation, and F_y,k is the emitted intensity at k by the y excitation. Since the Ca²⁺-bound form of Fura-2-FF does not generate fluorescence at the 400 nm emission, we can describe this by setting d to zero. When the florescence ratio R is the ratio F_x,k/F_y,k,

(4a)

R = \frac{a \cdot D_{f} + b \cdot D_{b}}{c \cdot D_{f}}

(5a)

\frac{D_{b}}{D_{f}} = \frac{c \cdot R - a}{b} = \frac{c}{b} \cdot (R - \frac{a}{c})

if all dye is the free form and [Ca²⁺] is zero, R is the minimum value (R_min) and equal to a/c. In addition, F_y,k is the maximum value (F_y,k,max) and is c·DT. If all dye is the Ca²⁺-bound form in Ca²⁺-saturated conditions, F_x,k is the maximum value (F_x,k,max) and is b·D_T. Therefore, [Ca²⁺] can be calculated with the following equation:

(6a)

[{Ca}^{2 +}] = K_{d} \cdot \frac{F_{y,k,max}}{F_{x,k,max}} \cdot (R - R_{min})

If x is the isosbestic excitation, (2a) and (5a) can be converted as follows:

(7a)

F_x,k=a'·D_T=a'·(D_f+D_b)

\frac{D_{b}}{D_{f}} = \frac{c \cdot R - a′}{a′} = \frac{c}{a′} \cdot (R - \frac{a′}{c})

Since a'/c equals Rmin, the following equation can be derived:

[{Ca}^{2 +}] = K_{d} \cdot \frac{1}{R_{min}} \cdot (R - R_{min}) .

The English in this document has been checked by at least two professional editors, both native speakers of English. For a certificate, please see:

http://www.textcheck.com/certificate/iNNy9q

References

1. Bers DM. Ca influx and sarcoplasmic reticulum Ca release in cardiac muscle activation during postrest recovery. Am J Physiol. 1985; 248:H366–H381. PMID: 2579587.

2. Wier WG. Cytoplasmic [Ca²⁺] in mammalian ventricle: dynamic control by cellular processes. Annu Rev Physiol. 1990; 52:467–485. PMID: 2184764.

3. Bers DM. Cardiac excitation-contraction coupling. Nature. 2002; 415:198–205. PMID: 11805843.

4. Duchen MR. Mitochondria in health and disease: perspectives on a new mitochondrial biology. Mol Aspects Med. 2004; 25:365–451. PMID: 15302203.

5. Raffaello A, Rizzuto R. Mitochondrial longevity pathways. Biochim Biophys Acta. 2011; 1813:260–268. PMID: 20950653.

6. Rizzuto R, Bernardi P, Pozzan T. Mitochondria as all-round players of the calcium game. J Physiol. 2000; 529(Pt 1):37–47. PMID: 11080249.

7. Griffiths EJ. Mitochondrial calcium transport in the heart: physiological and pathological roles. J Mol Cell Cardiol. 2009; 46:789–803. PMID: 19285504.

8. O'Rourke B, Cortassa S, Aon MA. Mitochondrial ion channels: gatekeepers of life and death. Physiology (Bethesda). 2005; 20:303–315. PMID: 16174870.

9. Gunter TE, Buntinas L, Sparagna G, Eliseev R, Gunter K. Mitochondrial calcium transport: mechanisms and functions. Cell Calcium. 2000; 28:285–296. PMID: 11115368.

10. Sparagna GC, Gunter KK, Sheu SS, Gunter TE. Mitochondrial calcium uptake from physiological-type pulses of calcium. A description of the rapid uptake mode. J Biol Chem. 1995; 270:27510–27515. PMID: 7499209.

11. Buntinas L, Gunter KK, Sparagna GC, Gunter TE. The rapid mode of calcium uptake into heart mitochondria (RaM): comparison to RaM in liver mitochondria. Biochim Biophys Acta. 2001; 1504:248–261. PMID: 11245789.

12. Beutner G, Sharma VK, Giovannucci DR, Yule DI, Sheu SS. Identification of a ryanodine receptor in rat heart mitochondria. J Biol Chem. 2001; 276:21482–21488. PMID: 11297554.

13. Beutner G, Sharma VK, Lin L, Ryu SY, Dirksen RT, Sheu SS. Type 1 ryanodine receptor in cardiac mitochondria: transducer of excitation-metabolism coupling. Biochim Biophys Acta. 2005; 1717:1–10. PMID: 16246297.

14. Carafoli E, Tiozzo R, Lugli G, Crovetti F, Kratzing C. The release of calcium from heart mitochondria by sodium. J Mol Cell Cardiol. 1974; 6:361–371. PMID: 4855051.

15. Brand MD. The stoichiometry of the exchange catalysed by the mitochondrial calcium/sodium antiporter. Biochem J. 1985; 229:161–166. PMID: 3929768.

16. Jung DW, Baysal K, Brierley GP. The sodium-calcium antiport of heart mitochondria is not electroneutral. J Biol Chem. 1995; 270:672–678. PMID: 7822294.

17. Poburko D, Potter K, van Breemen E, Fameli N, Liao CH, Basset O, Ruegg UT, van Breemen C. Mitochondria buffer NCX-mediated Ca²⁺-entry and limit its diffusion into vascular smooth muscle cells. Cell Calcium. 2006; 40:359–371. PMID: 16806462.

18. Gunter TE, Chace JH, Puskin JS, Gunter KK. Mechanism of sodium independent calcium efflux from rat liver mitochondria. Biochemistry. 1983; 22:6341–6351. PMID: 6661437.

19. Wingrove DE, Gunter TE. Kinetics of mitochondrial calcium transport. I. Characteristics of the sodium-independent calcium efflux mechanism of liver mitochondria. J Biol Chem. 1986; 261:15159–15165. PMID: 3771569.

20. Bers DM. Excitation-contraction coupling and cardiac contractile force. 2nd ed. Dordrecht, Netherlands: Kluwer Academic;2001.

21. Crompton M, Moser R, Lüdi H, Carafoli E. The interrelations between the transport of sodium and calcium in mitochondria of various mammalian tissues. Eur J Biochem. 1978; 82:25–31. PMID: 23291.

22. Griffiths EJ, Halestrap AP. Pyrophosphate metabolism in the perfused heart and isolated heart mitochondria and its role in regulation of mitochondrial function by calcium. Biochem J. 1993; 290:489–495. PMID: 8383966.

23. Allen SP, Stone D, McCormack JG. The loading of fura-2 into mitochondria in the intact perfused rat heart and its use to estimate matrix Ca²⁺ under various conditions. J Mol Cell Cardiol. 1992; 24:765–773. PMID: 1383555.

24. Miyata H, Silverman HS, Sollott SJ, Lakatta EG, Stern MD, Hansford RG. Measurement of mitochondrial free Ca²⁺ concentration in living single rat cardiac myocytes. Am J Physiol. 1991; 261:H1123–H1134. PMID: 1928394.

25. Du C, MacGowan GA, Farkas DL, Koretsky AP. Calibration of the calcium dissociation constant of Rhod(2)in the perfused mouse heart using manganese quenching. Cell Calcium. 2001; 29:217–227. PMID: 11243930.

26. Paredes RM, Etzler JC, Watts LT, Zheng W, Lechleiter JD. Chemical calcium indicators. Methods. 2008; 46:143–151. PMID: 18929663.

27. Hyrc KL, Bownik JM, Goldberg MP. Ionic selectivity of low-affinity ratiometric calcium indicators: mag-Fura-2, Fura-2FF and BTC. Cell Calcium. 2000; 27:75–86. PMID: 10756974.

28. Dong Z, Saikumar P, Griess GA, Weinberg JM, Venkatachalam MA. Intracellular Ca²⁺ thresholds that determine survival or death of energy-deprived cells. Am J Pathol. 1998; 152:231–240. PMID: 9422540.

29. Zhao M, Hollingworth S, Baylor SM. AM-loading of fluorescent Ca²⁺ indicators into intact single fibers of frog muscle. Biophys J. 1997; 72:2736–2747. PMID: 9168048.

30. Golovina VA, Blaustein MP. Spatially and functionally distinct Ca²⁺ stores in sarcoplasmic and endoplasmic reticulum. Science. 1997; 275:1643–1648. PMID: 9054358.

31. London RE, Rhee CK, Murphy E, Gabel S, Levy LA. NMR-sensitive fluorinated and fluorescent intracellular calcium ion indicators with high dissociation constants. Am J Physiol. 1994; 266:C1313–C1322. PMID: 8203496.

32. Weinberg JM, Davis JA, Venkatachalam MA. Cytosolic-free calcium increases to greater than 100 micromolar in ATP-depleted proximal tubules. J Clin Invest. 1997; 100:713–722. PMID: 9239420.

33. Chance B, Schoener B, Oshino R, Itshak F, Nakase Y. Oxidation-reduction ratio studies of mitochondria in freeze-trapped samples. NADH and flavoprotein fluorescence signals. J Biol Chem. 1979; 254:4764–4771. PMID: 220260.

34. Eng J, Lynch RM, Balaban RS. Nicotinamide adenine dinucleotide fluorescence spectroscopy and imaging of isolated cardiac myocytes. Biophys J. 1989; 55:621–630. PMID: 2720061.

35. Brandes R, Bers DM. Simultaneous measurements of mitochondrial NADH and Ca²⁺ during increased work in intact rat heart trabeculae. Biophys J. 2002; 83:587–604. PMID: 12124250.

36. Jo H, Noma A, Matsuoka S. Calcium-mediated coupling between mitochondrial substrate dehydrogenation and cardiac workload in single guinea-pig ventricular myocytes. J Mol Cell Cardiol. 2006; 40:394–404. PMID: 16480740.

37. Grynkiewicz G, Poenie M, Tsien RY. A new generation of Ca²⁺ indicators with greatly improved fluorescence properties. J Biol Chem. 1985; 260:3440–3450. PMID: 3838314.

38. Miller DJ, Smith GL. EGTA purity and the buffering of calcium ions in physiological solutions. Am J Physiol. 1984; 246:C160–C166. PMID: 6421170.

39. Smith GL, Miller DJ. Potentiometric measurements of stoichiometric and apparent affinity constants of EGTA for protons and divalent ions including calcium. Biochim Biophys Acta. 1985; 839:287–299. PMID: 2985122.

40. McGuigan JA, Kay JW, Elder HY. Critical review of the methods used to measure the apparent dissociation constant and ligand purity in Ca²⁺ and Mg²⁺ buffer solutions. Prog Biophys Mol Biol. 2006; 92:333–370. PMID: 16887174.

41. Schubert J. The use of ion exchangers for the determination of physical-chemical properties of substances, particularly radiotracers, in solution; theoretical. J Phys Colloid Chem. 1948; 52:340–350. PMID: 18906407.

42. Ebashi S. Calcium binding activity of vesicular relaxing factor. J Chir (Paris). 1961; 50:236–244.

43. Page E. Quantitative ultrastructural analysis in cardiac membrane physiology. Am J Physiol. 1978; 235:C147–C158. PMID: 364994.

44. Page E, McCallister LP, Power B. Sterological measurements of cardiac ultrastructures implicated in excitation-contraction coupling. Proc Natl Acad Sci U S A. 1971; 68:1465–1466. PMID: 5283936.

45. Malgaroli A, Milani D, Meldolesi J, Pozzan T. Fura-2 measurement of cytosolic free Ca²⁺ in monolayers and suspensions of various types of animal cells. J Cell Biol. 1987; 105:2145–2155. PMID: 3680375.

46. Denton RM, McCormack JG. On the role of the calcium transport cycle in heart and other mammalian mitochondria. FEBS Lett. 1980; 119:1–8.

47. Denton RM, McCormack JG. Ca²⁺ transport by mammalian mitochondria and its role in hormone action. Am J Physiol. 1985; 249:E543–E554. PMID: 2417490.

48. Denton RM, McCormack JG. Ca²⁺ as a second messenger within mitochondria of the heart and other tissues. Annu Rev Physiol. 1990; 52:451–466. PMID: 2184763.

49. Hansford RG. Relation between mitochondrial calcium transport and control of energy metabolism. Rev Physiol Biochem Pharmacol. 1985; 102:1–72. PMID: 2863864.

50. Hansford RG. Relation between cytosolic free Ca²⁺ concentration and the control of pyruvate dehydrogenase in isolated cardiac myocytes. Biochem J. 1987; 241:145–151. PMID: 2436608.

51. McCormack JG, Halestrap AP, Denton RM. Role of calcium ions in regulation of mammalian intramitochondrial metabolism. Physiol Rev. 1990; 70:391–425. PMID: 2157230.

52. Kirichok Y, Krapivinsky G, Clapham DE. The mitochondrial calcium uniporter is a highly selective ion channel. Nature. 2004; 427:360–364. PMID: 14737170.

53. Al-Nasser I, Crompton M. The reversible Ca²⁺-induced permeabilization of rat liver mitochondria. Biochem J. 1986; 239:19–29. PMID: 3099778.

54. Crompton M. The mitochondrial permeability transition pore and its role in cell death. Biochem J. 1999; 341:233–249. PMID: 10393078.

55. Halestrap AP, Clarke SJ, Javadov SA. Mitochondrial permeability transition pore opening during myocardial reperfusion--a target for cardioprotection. Cardiovasc Res. 2004; 61:372–385. PMID: 14962470.

56. Halestrap AP, McStay GP, Clarke SJ. The permeability transition pore complex: another view. Biochimie. 2002; 84:153–166. PMID: 12022946.

57. Rasmussen H, Barrett PQ. Calcium messenger system: an integrated view. Physiol Rev. 1984; 64:938–984. PMID: 6330778.

58. Gunter TE, Gunter KK, Sheu SS, Gavin CE. Mitochondrial calcium transport: physiological and pathological relevance. Am J Physiol. 1994; 267:C313–C339. PMID: 8074170.

59. Carafoli E, Lehninger AL. A survey of the interaction of calcium ions with mitochondria from different tissues and species. Biochem J. 1971; 122:681–690. PMID: 5129264.

60. Carafoli E. Mitochondria, Ca²⁺ transport and the regulation of heart contraction and metabolism. J Mol Cell Cardiol. 1975; 7:83–87. PMID: 123597.

61. Peverly JH, Miller RJ, Malone C, Koeppe DE. Ultrastructural evidence for calcium phosphate deposition by isolated corn shoot mitochondria. Plant Physiol. 1974; 54:408–411. PMID: 16658899.

Fig. 1

A microfluorometry system for multiparameric measurement. The diagram shows the instrumentation used to measure NADH (emission, 450 nm; excitation, 361 nm), Fura-2-FF (emission, 500 nm; excitation, 353 and 400 nm), and TMRE (emission, 590 nm; excitation, 530 nm) or carboxy-SNARF-1 (emission, 590 and 640nm; excitation, 539 nm). The light from a Xenon arc lamp excited the fluoroprobes in a myocyte, and then the emission passed through a dichroic mirror and band-pass filters to measure the intensity using photon-counting devices. Near infrared from a microscope was used as a light source to visualize the myocytes during experiments using a CCD camera and monitor.

Fig. 2

The excitation spectrum of NADH-Fura-2-FF. The spectrum shows the interference between NADH and Fura-2-FF at each emission (450 and 500 nm). (A) The NADH excitation spectrum at 450-nm emission. (B) The NADH excitation spectrum at 500-nm emission. (C) The Fura-2-FF excitation spectrum at 450-nm emission under Ca²⁺-free and 1 mM Ca²⁺ conditions. (D) The Fura-2-FF excitation spectrum at 500-nm emission under Ca²⁺-free and 1 mM Ca²⁺ conditions.

Fig. 3

NADH and Fura-2 excitation and emission spectra. (A) The NADH excitation spectrum was obtained at 465-nm emission and the emission spectrum was obtained at 365-nm excitation. (B) The Fura-2 excitation spectrum was obtained at 500-nm emission and the emission spectrum was obtained at 340-nm excitation. The emission spectrum was shifted to the left by an increase in Ca²⁺. Ex is excitation. Em is emission.

Fig. 4

Identification of isosbestic points. (A) The isosbestic point at 450-nm emission (red arrow). Ca²⁺ in the non-bound state (- -) and Ca²⁺ in the bound state (-) (B) The isosbestic point at 500-nm emission for Ca²⁺ in the non-bound state (- -) and Ca²⁺ in the bound state (-) (C) The graph shows subtracted data. Ca²⁺ in the non-bound state was subtracted from that in the bound state at 450 nm. (D) The graph shows subtracted data. Ca²⁺ in the non-bound state was subtracted from that in the bound state at 500 nm. (E) Standard deviation data from graph C. (F) Standard deviation data from graph D.

Fig. 5

Measurement of RN factors. (A) The NADH signal in Fura-2-FF-free myocytes at 361-nm excitation and 450-nm emission was measured in the presence of various mitochondrial substrates. (B) F_400,500 (●) and F_353,500 (-) were measured simultaneously to monitor the NADH contribution to the Fura-2-FF signal. (C) The graph shows the relationships between F_361,450,NADH and F_353,500,NADH (●) and between F_361,450,NADH and F_400,500,NADH (○). Linear relationships are evident in the graph.

Fig. 6

Cellular area-dependent autofluorescent background. ● (F_361,450) was used for NADH signal correction. ○ (F_353,500) and ▾ (F_400,500) were used for Fura-2-FF signal correction, respectively. ▵ (F_530,590) was used for TMRE signal correction.

Fig. 7

Simultaneous measurement of NADH, [Ca²⁺]_m, and pH. Using carboxy-SNARF- and Fura-2-FF-loaded myocytes, NADH, [Ca²⁺]_m, and pH was measured simultaneously. The mitochondrial pH changes were investigated following Ca²⁺ changes. The increase in [Ca²⁺]_m did not affect mitochondrial pH. Mitochondrial pH was 7.504±0.047 (mean±S.E., n=13).

Fig. 8

Results of NADH and Fura-2-FF interference correction. The left panels show the signals prior to correction and the right panels show the signals after correction. NADH and the ratio of Fura-2-FF signals were changed following correction. The calculated [Ca²⁺]_m was substantially decreased. (A) NADH signals at 450-nm emission. (B) Fura-2-FF signals at 500-nm emission. The figure shows F_400,500 (- -), F_353,500 (----), and the ratio of Fura-2-FF (-). (C) The mitochondrial calcium concentration calculated from the Fura-2-FF ratio.

Fig. 9

Resting and maximal [Ca²⁺]_m at l µM cytosolic Ca²⁺. The resting [Ca²⁺]_m was 1.03±0.13 µM (mean±S.E., n=32) and the maximal [Ca²⁺]_m was 29.6±1.61 µM (mean±S.E., n=33).

Fig. 10

Simultaneous measurement of NADH, [Ca²⁺]_m, and Ψ_m. Using Fura-2-FF-loaded myocytes, NADH, [Ca²⁺]_m, and Ψ_m were measured simultaneously. The resting Ψ_m was assumed to be -150 mV.

Table 1

The dissociation constant (K_d) of Fura-2-FF at different pH values

TOOLS

Similar articles