Abstract
Purpose
To introduce a new convenient and accurate method to measure the angle kappa using ultrasound biomicroscopy (UBM) and corneal topography.
Methods
Data from 42 eyes (13 males and 29 females) were analyzed in this study. The angle kappa was measured using Orbscan II and calculated with UBM and corneal topography. The angle kappa of the dominant eye was compared with measurements by Orbscan II.
Results
The mean patient age was 36.4 ± 13.8 years. The average angle kappa measured by Orbscan II was 3.98° ± 1.12°, while the average angle kappa calculated with UBM and corneal topography was 3.19° ± 1.15°. The difference in angle kappa measured by the two methods was statistically significant (p < 0.001). The two methods showed good reliability (intraclass correlation coefficient, 0.671; p < 0.001). Bland-Altman plots were used to demonstrate the agreement between the two methods.
Angle kappa is the angle between the visual axis and the pupillary axis. Each eye has a different angle kappa, and they are usually less than 5° [123].
Angle kappa is clinically significant because it can lead to alignment errors during photo ablation in laser refractive surgery, as well as lens decentration during intraocular refractive surgery [3]. The decentration of ablation zones can lead to undercorrection and irregular astigmatism [34]. Also, the presence of a large angle kappa is important to consider when planning strabismus surgery.
Various methods can be used to measure the angle kappa. Precise measurements can be obtained using a synoptophore or a major amblyoscope; however, these instruments are not commonly found in clinical offices. Recently, newer devices such as Orbscan II (Bausch & Lomb, Rochester, NY, USA), Galilei (Ziemer Ophthalmic Systems, Port, Switzerland), and OPD Scan II (Nidek, Gamagori, Japan) have become commercially available and can be used to evaluate angle kappa [1567]. Basmak et al. [2] compared the reliability of a synoptophore and Orbscan II.
Herein, we present our findings after designing a new method using ultrasound biomicroscopy (UBM) and corneal topography to conveniently and accurately measure angle kappa.
Data from 42 eyes examined between April 2015 and June 2015 were obtained from the Chung-Ang University Hospital database; all medical records were reviewed retrospectively. We excluded individuals with a history of intraocular and/or extraocular surgery, strabismus, best-corrected visual acuity <20 / 20 and age <18. This study was approved by the institutional review board of Chung-Ang University Hospital, and all procedures conformed to the guidelines of the Declaration of Helsinki.
UBM (AVISO; Quantel Medical, Clermont-Ferrand, France) and two corneal topography systems (Orbscan II, Bausch & Lomb/Humphrey Atlas 995 corneal topography; Carl Zeiss Meditec, Dublin, CA, USA) had been performed on all enrolled participants for purposes other than estimating angle kappa. A single ophthalmologist (JHY) conducted all examinations.
Orbscan II was used to measure the angle kappa in all participants. Only one measurement was performed on each eye unless an unacceptable result was obtained and had to be repeated. In preparation for Orbscan II measurements, all participants were instructed to maintain the correct head position and a straight gaze. The examiner used the device joystick to make adjustments so that the final result would be a sharply focused image of the eye.
Participants were asked to look at a blinking light in the center of an ultrasound probe. The probe was then placed in contact with the anesthetized cornea, and 10 programmed consecutive measurements of axial length were recorded. Anterior chamber depth was automatically calculated from the first ultrasound peak to the aqueous-anterior lens interface peak. Humphrey Atlas 995 corneal topography, which displays X-Y Cartesian coordinates between the corneal vertex and pupil center, was also performed.
The pupillary axis is the line passing through the center of the pupil perpendicular to the cornea (Fig. 1A). In Fig. 1B, schema ABC is composed of three points: the center of the pupil, the point of the cornea that falls on the pupillary axis, and the point of the cornea that lies within the line of sight. The angle between AC and BC is angle lambda, which is nearly identical to angle kappa (Fig. 1A and 1B). Lines AB and BD have almost the same length. Using Humphrey Atlas 995 corneal topography, we determined the points for the pupil center and the cornea vertex. The distance between these two points was nearly the same as the length of BD. The length of AC is the anterior chamber depth, which is nearly the same as the length of CD. Because CD is the same as the anterior chamber depth, angle kappa can be measured by calculating the BCD tangent. Herein, we refer to these values as angle kappa. We used Microsoft Excel (Microsoft, Redmond, WA, USA) to elicit angle kappa from the BCD tangent.
The patient was instructed to extend both arms, bring both hands together, and create a small opening. At that point, with both eyes open, patients were instructed to look at a distant object through the opening in their hands. The patient then alternated closing their eyes to determine which eye was viewing the object. Kim and Cho [8] reported that as angle kappa gets smaller, the eye is less affected by errors induced by the cornea and lens. Thus, the fovea of the dominant eye can be perceived more vividly in images. We compared the angle kappa values of the patients' dominant eyes.
Data were analyzed using SPSS ver. 19.0 (IBM Corp., Armonk, NY, USA). The angle kappas measured using Orbscan II and by UBM and corneal topography were compared using paired t-tests. Correlations between angle kappas measured with the two methods were statistically examined using the intraclass correlation coefficient. A Bland-Altman plot was used to evaluate agreement and estimate confidence intervals. Statistical significance was defined by a p-value <0.05.
We included 42 eyes of 42 patients. The average patient age was 36.4 ± 13.8 years (Table 1). Angle kappa measured by Orbscan II averaged 3.98° ± 1.12°, and angle kappa calculated by UBM and corneal topography averaged 3.19° ± 1.15°. Paired t-test analysis showed a statistically significant difference between the two methods (p < 0.001) (Table 2). Furthermore, the two tests showed good reliability (intraclass correlation coefficient, 0.671; p < 0.001).
Fig. 2 shows the Bland-Altman plot of all 42 eyes. The agreement between the two methods was moderate with a systematic deviation of 0.79° and a 95% confidence interval of −1.47 to 3.04.
According to Landolt's original definition, the visual axis is the broken line connecting the fovea to the fixation point, and this line passes through the nodal point of the eye [4]. However, the nodal point is a purely theoretical concept, and angle kappa, as originally defined by Landolt, cannot be measured [19]. Le Grand and El Hage [10] redefined angle kappa as the angular distance between the line of sight (line connecting the pupillary center and the fixation point) and the pupillary axis. Both angles will be nearly identical when the point of fixation is not very close to the eye [10]. Because the two angles are easily confused in other studies [911], we referred to the measured angle as angle kappa.
Using a synoptophore or major amblyoscope, exact kappa angle calculation is possible. Using a small fixation point and a Purkinje image, the angular distance can be measured by moving the Purkinje image along a graduated arc to the center of the pupil. However, these devices are rarely available in office settings. Newly developed devices, such as Orbscan II, OPD scan II, and Galilei, have been widely used for measuring the angle kappa. The Orbscan II corneal topography system is a three-dimensional scanning slit topographic device that automatically determines angle kappa with special software that measures the distance between the center of the pupil and the center of the placido ring, which was reflected on the cornea. The placido ring center represents the axis of sight [2]. We compared our method with Orbscan II using a similar principle.
Hashemi et al. [12] measured the angle kappa in 800 eyes using Orbscan II and found a mean angle kappa value of 5.46° ± 1.33°. London and Wick [9] reported that the mean angle kappa value for adults was 5.08°. In our study, both angle kappa using UBM and corneal topography (mean ± standard deviation [SD], 3.19° ± 1.15°) and angle kappa using Orbscan II (mean ± SD, 3.98° ± 1.12°) were lower than those from previous studies performed on participants of different races. However, Kim and Cho [8] reported a mean angle kappa for a Korean population of 3.91° ± 1.54°, which was similar to our result using Orbscan II.
There are several explanations for why angle kappa in our study was smaller than those reported in previous studies. First, more than 60% of our patients were myopic. According to the literature [213], angle kappa is smallest among myopes and largest among hyperopes. These other studies also reported that angle kappa values decreased significantly toward negative refractive errors in the myopic group. In contrast, in the hyperopic group, a correlation existed between the large positive angle and positive refractive error. The mean angle kappa of myopic patients in our study was 3.14°, while the mean angle kappa of our hyperopic patients was 3.50°.
According to the literature, angle kappa decreases with age [912]. Our patients' mean age was 36.4 ± 13.8 years. Compared with another study population with a younger average age (24.21 ± 1.21 years, by Kim and Cho [8]), the older study population had lower angle kappa values.
There have been numerous studies assessing the agreement among devices that measure anterior chamber depth. Reddy et al. [14] and Al Farhan [15] reported that contact-based devices resulted in lower measurements for anterior chamber depth compared with Orbscan II and IOLMaster. Meanwhile, Vetrugno et al. [16] reported that optical measurement of the anterior chamber depth with Orbscan II yielded a small underestimation. In clinical practice, various devices such as UBM, Pentacam, Orbscan II, and IOLMaster are being used to measure anterior chamber depth. In this study, the anterior chamber depth measured by UBM (3.43 ± 0.30 mm) was significantly longer than that measured automatically with Orbscan II (2.95 ± 0.31 mm, p < 0.001). Because the anterior chamber depth is the denominator of angle kappa in our method, we concluded that longer anterior chamber depths result in smaller angle kappas.
According to Kim and Cho [8], angle kappa is significantly smaller in the dominant eye than in the non-dominant eye. In our study, angle kappa values of the dominant eyes were compared. Therefore, this also helps to explain the relatively low angle kappa values from our data.
Although the difference between two methods was around −1.47° to 3.04° (95% limitation of agreement), the mean difference was only 0.79°. Basmak et al. [2] reported that angle kappa values obtained by Orbscan II were significantly higher in all groups compared to synoptophore, ranging from 1.89° to 2.82°. Also, Dominguez-Vicent et al. [7] reported that the mean difference in angle kappa measured with the Orbscan II and the Galilei G4 was 3.60°. As compared with this previous study, the difference in our study was relatively small. Agreement of angle kappa measurements between the two methods was moderate to good. There was a systematic trend of relatively lower measurements when angle kappa was measured by UBM and corneal topography, with 95% of the measurements falling within 2.2° of the angle kappa measure by Orbscan II. This relationship was valid for a wide range of degrees. The results are thus comparable with Orbscan II measurements.
This study has several limitations. First, angle kappa measurements by UBM and corneal topography are more likely to have errors when the cornea shape is excessively simplified, as in our method. Our new method showed two cases located higher than 95% limitation of agreement in the Bland-Altman plot. In those cases, the measured distances between the pupil center and the cornea vertex were 0. It was likely to be an error on the test. Second, there is controversy regarding the comparability of anterior chamber depth measurements performed with other devices [141617]. We calculated angle kappa differently according to anterior chamber depth and using different devices. For this reason, when comparing the changes in angle kappa for each individual, anterior chamber depth must always be measured the same way and using the same device. Third, we did not compare our method with other methods, such as using a synoptophore or amblyoscope. Fourth, although angle kappa was taken into account frequently when performing Hirschberg or Krimsky tests in young and uncooperative patients in order to improve surgical results, individuals under the age of 18 were excluded in this study due to their low cooperation. Last, our method required additional calculation to obtain a n angle kappa. However, it can be simply calculated by Microsoft Excel or other free calculation software (http://www.rapidtables.com/calc/math/Tan_Calculator.htm).
In conclusion, we designed a new method to calculate angle kappa using UBM and corneal topography. This method utilizes common office instruments, allowing for quick and easy evaluation of eyeball deviation. This method also allows for the estimation of angle kappa using previous examination data.
Figures and Tables
Fig. 1
(A) Schematic representation of the angle kappa components. (B) Schematic diagram showing how to measure angle kappa using ultrasound biomicroscopy and corneal topography. κ = angle kappa; λ = angle lambda; A = point of the cornea that falls on the pupillary axis; B = point of the cornea that lies within the line of sight; C = center of the pupil; D = point of the pupillary axis that meets the vertical line that passes through point B.
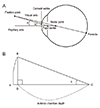
Fig. 2
Bland-Altman plots showing agreement between the two methods. Bold line shows the mean of the difference between the two methods; the dashed line indicates the 95% limit of agreement. UBM = ultrasound biomicroscopy.

References
1. Park CY, Oh SY, Chuck RS. Measurement of angle kappa and centration in refractive surgery. Curr Opin Ophthalmol. 2012; 23:269–275.
2. Basmak H, Sahin A, Yildirim N, et al. Measurement of angle kappa with synoptophore and Orbscan II in a normal population. J Refract Surg. 2007; 23:456–460.
3. Emsley HH, editor. Visual optics. 5th ed. London: Hatton Press;1952. p. 523.
4. Uozato H, Guyton DL. Centering corneal surgical procedures. Am J Ophthalmol. 1987; 103(3 Pt 1):264–275.
5. Sung YJ, Nam SM, Lew H. Measurement of angle lambda using pentacam in normal and exotropic children. J Korean Ophthalmol Soc. 2015; 56:1263–1267.
6. Hernandez-Camarena JC, Chirinos-Saldana P, Navas A, et al. Repeatability, reproducibility, and agreement between three different Scheimpflug systems in measuring corneal and anterior segment biometry. J Refract Surg. 2014; 30:616–621.
7. Dominguez-Vicent A, Monsalvez-Romin D, Perez-Vives C, et al. Measurement of angle kappa with Orbscan II and Galilei G4: effect of accommodation. Graefes Arch Clin Exp Ophthalmol. 2014; 252:249–255.
8. Kim HK, Cho KJ. The angle kappa in dominant and non-dominant eye. J Korean Ophthalmol Soc. 2015; 56:494–498.
9. London R, Wick BC. Changes in angle lambda during growth: theory and clinical applications. Am J Optom Physiol Opt. 1982; 59:568–572.
10. Le Grand Y, El Hage SG, editors. Physiological optics. New York: Springer-Verlag;1980. p. 73.
11. Braaf B, van de Watering TC, Spruijt K, et al. Calculating angle lambda (λ) using zernike tilt measurements in specular reflection corneal topography. J Optom. 2009; 2:207–214.
12. Hashemi H, KhabazKhoob M, Yazdani K, et al. Distribution of angle kappa measurements with Orbscan II in a population-based survey. J Refract Surg. 2010; 26:966–971.
13. Choi SR, Kim US. The correlation between angle kappa and ocular biometry in Koreans. Korean J Ophthalmol. 2013; 27:421–424.
14. Reddy AR, Pande MV, Finn P, El-Gogary H. Comparative estimation of anterior chamber depth by ultrasonography, Orbscan II, and IOLMaster. J Cataract Refract Surg. 2004; 30:1268–1271.
15. Al Farhan HM. Agreement between Orbscan II, VuMAX UBM and Artemis-2 very-high frequency ultrasound scanner for measurement of anterior chamber depth. BMC Ophthalmol. 2014; 14:20.
16. Vetrugno M, Cardascia N, Cardia L. Anterior chamber depth measured by two methods in myopic and hyperopic phakic IOL implant. Br J Ophthalmol. 2000; 84:1113–1116.
17. Rozema JJ, Wouters K, Mathysen DG, Tassignon MJ. Overview of the repeatability, reproducibility, and agreement of the biometry values provided by various ophthalmic devices. Am J Ophthalmol. 2014; 158:1111–1120.e1.




 PDF
PDF ePub
ePub Citation
Citation Print
Print



 XML Download
XML Download