Abstract
The current study proposes a model of the cardiovascular system that couples heart cell mechanics with arterial hemodynamics to examine the physiological role of arterial blood pressure (BP) in left ventricular hypertrophy (LVH). We developed a comprehensive multiphysics and multiscale cardiovascular model of the cardiovascular system that simulates physiological events, from membrane excitation and the contraction of a cardiac cell to heart mechanics and arterial blood hemodynamics. Using this model, we delineated the relationship between arterial BP or pulse wave velocity and LVH. Computed results were compared with existing clinical and experimental observations. To investigate the relationship between arterial hemodynamics and LVH, we performed a parametric study based on arterial wall stiffness, which was obtained in the model. Peak cellular stress of the left ventricle and systolic blood pressure (SBP) in the brachial and central arteries also increased; however, further increases were limited for higher arterial stiffness values. Interestingly, when we doubled the value of arterial stiffness from the baseline value, the percentage increase of SBP in the central artery was about 6.7% whereas that of the brachial artery was about 3.4%. It is suggested that SBP in the central artery is more critical for predicting LVH as compared with other blood pressure measurements.
There have been a number of recent studies examining the relationship between arterial wall stiffening and cardiac cellular overload (1, 2). However, despite substantial progress in understanding this issue, the detailed mechanisms underlying this relationship remain unclear. Therefore, a novel approach is required to delineate the causal relationship between arterial stiffness and heart hypertrophy. The use of computer simulations with mathematical models is an alternative method and has been widely used for the analysis of cardiovascular system dynamics (3-6).
Lumped models of the cardiovascular system are very simple and can be easily coupled with the nervous system for long-term simulation (7). However, the model cannot accurately predict microscopic phenomena in cells or tissues. To overcome this limitation, we proposed a cell-system integrated model of the cardiovascular system that included cardiac cells, the Laplace heart, and the vascular system (8-10). However, the cell-system model uses relatively a simple lumped model for the arterial system and lacks detailed information regarding arterial pressures and pulse wave velocity (PWV). On the other hand, mathematical models focusing on arterial hemodynamics have been proposed by several groups (11-13). These models have the ability to represent the spatial distribution of arterial hemodynamics and PWV. However, the time-varying capacitance heart model (14) was incorporated into these models by which the relationship between heart cellular mechanics and arterial hemodynamics could not be analyzed.
In this study, the arterial network model of Ozawa et al. (11) was incorporated into our previous cell-system model (8) to delineate the physiological relationship between arterial pressure and left ventricular hypertrophy (LVH). To verify the present method, we calculated the effects of arterial stiffness, arterial hemodynamics, and pulse wave velocity on cardiac cellular mechanics, and compared the results with experimental and clinical observations. Using this methodology, the physiological effects of arterial stiffness variation on LVH were assessed in an integrated manner.
To simulate heart mechanics and arterial pulse waves at a multiscale level, we developed an integrative mathematical model that combined cell excitation-contraction coupling with heart mechanics, system circulation, and hemodynamics of the arterial network. In our previous studies (8, 10), we combined the ventricular cell model with the Negroni and Lascano model (NL model) (15) and eventually with system circulation. Here, we used the same approach for the atrial and ventricular models, but with the addition of arterial network branches (Fig. 1).
As described in our previous report (10), the present computational approach to cardiac cells is based on the electrophysiological models of human atrial and ventricular myocytes proposed by Nygren et al. (16) and ten Tusscher et al. (17) (TNNP model), respectively. In addition, these cellular electrophysiological models were combined with the NL model of cross-bridge dynamics (CBD) for contraction (18). Cross-bridge dynamics in the NL model are described by a four-state system consisting of free troponin (T), Ca2+-bound troponin (TCa), Ca2+-bound troponin with attached cross-bridges (TCa*), and troponin with attached cross-bridges (T*). The total force (F) of a single muscle unit is given by the following relationship:
where Fb is the equivalent cross-bridge force generated by the contribution of all cross-bridges attached in parallel within the muscle unit and Fp is the force developed by the elastic element of the muscle unit. The cross-bridge force generated in (a) is presented as follows, according to the NL paper (15):
where A is the model parameter and h is the cross-bridge elongation length. The related parameters in the NL models are presented in Table 1.
The forces obtained from the cell-NL models were converted into atrial and ventricular pressures by applying Laplace's law to the atrial and ventricular models. In our previous report, we referred to this type of heart model as a biological Laplace heart (BLH) (9). The NL, as well as the spherical atrial and ventricle models, were explained in detail in our previous reports (8, 9).
We used a lumped parameter model to simulate a cardiovascular system. With the exception of the heart and arterial compartments, the hemodynamic elements were the same as those described by Heldt et al. (19). The entire model is shown in Fig. 2. The peripheral circulation is divided into the upper body, renal, splanchnic, and lower extremity sections; the intrathoracic superior, inferior vena cava, and extrathoracic vena cava are identified separately. The model thus consists of compartments, each of which is represented by a linear resistance (R) and compliance (C) that can be either linear, nonlinear, or time-varying. The NL model and Laplace's law were applied to calculate heart mechanics. All of the related parameters in the systemic circulation model are presented in Table 2.
The arterial network model proposed by Ozawa et al. (11) was incorporated into the current cell-system model system as shown in Fig. 2. Model of Ozawa et al. was based on the numerical solution of one-dimensional equations for fluid and vessel wall motion in a geometrically accurate branching network of the arterial system (28 elements), including energy losses at bifurcations. Blood flow and pulse wave propagation in each element were described by one-dimensional Navier-Stokes equations with axial velocity, fluid pressure, and vessel cross-sectional area as variables (14). These equations were solved using the finite difference method on one-dimensional meshes for each element of the arterial network branches (14). Rebound of arterial waves from terminal or bifurcation branches were numerically implemented through boundary conditions. As similar to Ozawa et al. (11), we used the method of charateristics for the boundary conditions. Detailed specifications of the four large arteries in the arterial network are shown in Table 3. The total length of the four arteries was 37.9 cm, and the length of the thoracic aorta was about half (48.8%) of the total length, with a mean diameter of 2 cm. In the normal case, wall stiffness values for the arterial elements were identical to those described in the Model of Ozawa et al. (11). To couple the arterial network model with BLH, we regarded the left ventricular (LV) pressure as the boundary condition of the arterial network model and the aortic flow rate as the input condition of the BLH model.
To investigate the effects of arterial wall stiffening on heart cellular mechanics and cardiovascular system dynamics, we performed a parametric study with respect to arterial wall stiffness, increasing arterial wall elasticity of the model by 1, 2, 3, and 4 times the normal value. However, this variation in arterial elasticity was assumed only in large arteries because the wall stiffness of small arteries remains nearly unchanged (21). Here, PWV was calculated from the distance and traveling time of the pressure wave between the ascending aorta (1st element of the arterial network in Fig. 2) and the abdominal aorta (4th element of the arterial network in Fig. 2).
To assess the feasibility of our cell-system-arterial network model, we plotted the sequential events from the cell level to that of the arterial pulse (Fig. 3) and reconstructed the shapes of the original action potential and Ca2+ transient. The action potential showed the characteristic spike notch dome shape of ventricular cells (Fig. 3A). Fig. 3B shows the transient increase in free calcium concentration within the cytoplasm. The force of muscle contraction develops rapidly in response to the Ca2+ transient in cells (Fig. 3C). Two components comprise this force: that generated by cross-bridges and elastic force. The LV active force showed a peak value of approximately 28 mN/mm2 (kPa). Fig. 3D shows the volume variation in the left atrium (LA) and LV relative to time. The ejection fraction of the left ventricle was nearly 0.58. The LA contracts prior to ventricular contraction. The timeline of the pressure changes observed in the aorta, atrium, and ventricle are shown in Fig. 3E. Here, the heart rate was assumed to be 72 bpm (beats/min). Pressure pulse waves at three arterial positions (ascending aorta, common iliac artery, and anterior tibial artery) are plotted in Fig. 3F and show increased pulse pressures and a smoothed dicrotic notch in the distal portion of the arterial branches.
To verify our model, the major hemodynamic variables generated by the model are compared with standard values in Table 4. The computed blood pressure is within the range considered to be physiologically normal within the general population. The stroke volume was approximately 73 mL. The cardiac output, which was obtained by multiplying the stroke volume with a heart rate of 72 bpm, was 5,256 mL/min. The computed value of the PWV in the aorta was within the range 4.4 to 8.5 m/sec, which is consistent with an experimental study in humans (22).
Fig. 4 shows the variation in pressure waves within the aorta according to arterial stiffness. Compared with the baseline value of arterial elasticity (En=4×106 dyne/cm2), with increases in arterial stiffness, the time delay of the pressure wave between the ascending and abdominal aortas decreased, whereas the difference in peak aortic pressures increased. As shown in Fig. 4A and B, increase of arterial stiffness by 2 times of normal value increased peak aortic pressure by nearly 8% (from 112.5 mmHg to 121.5 mmHg). However, the increased value is relatively small compared with in vivo experimental observation (23). Interestingly, in revers to the present cases, acute rise in blood pressure can increase in vivo arterial stiffness demonstrated by Stewart et al. (24). The relation between arterial stiffness and cardiac output is shown in Table 5.
At the cellular level, the cross-bridge elongation (CBEL) decreased sharply during contraction below the steady-state value (=5 nm) and then immediately reverted to the back to the steady-state value (Fig. 5A). Shortening of the CBEL below the steady-state value during contraction played a critical role in active force generation, as the calcium-bound troponin concentration was high during this period (Fig. 5B). This shortening of the elongation during contraction was accompanied by a decrease in the half sarcomere length (HSL) (Fig. 5C). The active force was generated by the product of the CBEL and the concentration of calcium-bound troponin (Fig. 5D).
There was no change in the amount of troponin bound to the cross-bridge with increasing arterial thickness (solid, thick, and thin dotted lines in Fig. 5B), whereas CBEL increased (Fig. 5A). Accordingly, the HSL and LV peak pressure (Fig. 5E) increased with arterial stiffness. According to increased stiffness, it is remarkable that the changes of CBEL and half sarcomere length during ventricular relaxation were relatively small compared with those during ventricular contraction.
The peak cellular stress observed with increases in arterial stiffness is shown in Fig. 6A. As shown in the Fig. 6, there was an initial steep increase in the peak cellular stress followed by a saturated pattern at higher arterial stiffness values. On the other hand, the variation in PWV was nearly linear with increasing arterial stiffness (Fig. 6B). Systolic blood pressures (SBP) in the ascending aorta and brachial artery also changed consistent with peak cellular stress (Fig. 6C). Interestingly, variation in aortic SBP was more prominent than that in the brachial arterial with respect to increasing arterial stiffness. Fig. 6D presents the relationship between PWV and peak cellular stress, showing a saturated pattern for higher values of PWV.
A major objective of the present study was to integrate cellular processes with systemic and arterial hemodynamics by which propagation of the arterial pulse wave is related to heart mechanics in the human circulatory system. Here, the arterial network model proposed by Ozawa et al. (11) could couple blood hemodynamics and pulse waves in detailed arteries with LV mechanics and systemic circulation. Our discussion of the computational results focuses on three main aspects: the plausibility of the integrative method of a cell-system-arterial network to simulate heart mechanics and cardiovascular hemodynamics, a parametric study focusing on arterial stiffness to delineate the relationship between arterial hemodynamics and cardiac cellular mechanics.
In the cell-system-arterial network model, electrophysiological variables such as the action potential, calcium concentration, and generated cellular forces in the cellular models were determined for atrial and ventricular cells (Fig. 3A-C). Computational results for the cardiovascular system dynamics were consistent with published results of pressure and volume variations in the LA and LV (Fig. 3D, E). Arterial pulse wave propagation along the arterial network also showed a pattern similar to previous clinical observations (Fig. 3F, 4). In conclusion, all sequential events from the cell to arterial pulse waves were well reproduced and consistent with the existing data, demonstrating the plausibility of the present method as an integrative analysis tool for evaluating heart mechanics and arterial hemodynamics.
Atherosclerosis is a symptom of aging that causes serious health problems. Specifically, it increases cardiac cellular stress, which eventually stimulates heart hypertrophy (23, 24). Roman et al. (25) investigated the effects of central blood pressure (BP) on left ventricular hypertrophy (LVH), and showed that systolic BP in the central artery (or the ascending aorta) is more important in stimulating LVH and inducing conformational changes and remodeling of the heart. With respect to medical terminology, central BP represents the BP in the large arteries, such as the ascending, descending, and abdominal aortas. Wang et al. (26) also reported that central systolic pressure is more critical than other blood pressures in predicting cardiovascular diseases. However, theoretical approaches to explain the detailed physiological mechanism underlying these effects have not been reported. Therefore, we proposed an integrative cell-system-arterial network model to delineate the relationships between heart cellular stress, LVH, and arterial stiffness.
Using this model, we performed a parametric study to evaluate the effects of stiffened arteries on heart cellular mechanics by increasing the vascular wall stiffness of the largest arteries in the model. Cross-bridge-generated contraction force (CBCF) (Fig. 5D), LV peak pressure (Fig. 5E), and PWV (Fig. 6B) increased, whereas HSL decreased with increasing arterial stiffness. Peak cellular stress and SBP in the brachial and central arteries also increased, but were saturated at higher values of arterial stiffness (Fig. 6A). As shown in Fig. 6C, central arterial stiffness could more affect SBP, which is because the half of ejected blood is stored in the vessel and three quarters of the blood is stored in aorta. Therefore, if the central artery becomes stiff, the SBP could be more affected. Interestingly, changes in the peak cellular stress and SBP showed similar patterns (Fig. 6A and C). In particular, SBP variation in the central artery (or ascending aorta) with respect to arterial stiffness was more prominent than that in the brachial artery) (Fig. 6C). As increases in exerted cellular stress indicate increased stimulation of LVH, this result clearly corresponds to the clinical observation that SBP in the central artery is more critical than other blood pressure measurements in predicting LVH. The peak cellular stress corresponding to a specific PWV can be inferred quantitatively from the graph shown in Fig. 6D. Clinically, cellular stress is not easy to observe in patients (27), while PWV can be measured easily. Therefore, this result provides another example of the utility of the present cell-system-arterial network model.
This study developed a cell-system-arterial network coupled model of the cardiovascular system. Although results were reasonable, the study has several limitations. First, we did not consider other effects, such as autonomic nerve control or changes in the resistance of the peripheral vessels involved in the arterial stiffening process. Therefore, we elucidated only the mechanisms involved in arterial stiffness perturbation, cellular contractility, and vascular hemodynamics. Second, the heart has a complex muscle layer with fiber anisotropy and heterogeneous muscle thickness. In addition, different parts of the ventricles are activated at different times. However, in this study, the ventricle was assumed to be a Laplace heart to reduce the complexity of the coupled cell-circulation hemodynamics method. Besides, in this study we didn't consider long-term compensatory mechanism of blood pressure through renal excretory system. Nevertheless, these limitations were not expected to markedly alter the main findings of this study.
Despite its limitations, our model can simulate the sequential events of the cardiovascular system from cells to the systemic circulation. Consequently, the model can be applied to perioperative intensive care in heart, lung and liver surgery which requires accurate evaluation of the pulmonary preload and systemic afterload. Along with clinical data, a computer model of the cardiovascular system can be a useful tool allowing clinicians to estimate critical information about patients' cardiovascular system, such as blood pressure, and the arterial pulse wave. In addition, clinicians can use the model to predict the cardiovascular changes induced in patients by treatment in intensive care units. For example, Kashif et al. (28) showed that a simulation method combined with clinical measurements can provide information about patients in intensive care. We expect that our model could play a similar role in estimating patient-specific data for grave patients. In the future, this will be delineated by combining the model with clinical data.
Figures and Tables
Fig. 1
Schematic of the integrative cell-system simulation model designed for effective multiscale numerical analysis from cellular to tissue mechanics. BLH, biological Laplace heart.
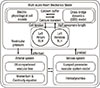
Fig. 2
Schematic of the integrative vascular system model. up, upper body; sup, superior vena cava; pa, pulmonary artery; pv, pulmonary vein; ro, right ventricular outflow; la, left atrium; lv, left ventricle; inf, inferior vena cava; ab, abdominal vena cava; kid, kidney; sp, splanchnic; ll, lower limbs; th, thoracic; rv, right ventricle.
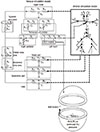
Fig. 3
Numerical simulation results of sequential events of the integrative cell-system-arterial network model. Dotted lines, atrial events; solid lines, ventricular events. (A) Action potential. (B) Ca2+ concentration. (C) Cellular forces (solid line: active force generated by cross-bridges, thick dotted line: passive elastic force at the ventricular myocyte). (D) Cardiac volume. (E) Blood pressure in the left atrium and left ventricle, respectively (thick dotted line: aorta pressure). (F) Pressure pulse waves at three arterial positions (ascending aorta, common iliac artery, and anterior tibial artery).
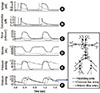
Fig. 4
Simulated results of propagation delay of arterial pressure waves between the ascending aorta and the abdominal aorta with respect to differences in arterial stiffness. (A) En, (B) 2En, (C) 4En. Here, En represents the normal stiffness of the large arteries.

Fig. 5
Simulated results of the inotropic state of the left ventricular BLH in the cell-system model. (A) Cross-bridge elongation length (CBEL). (B) Concentration of cross-bridge-attached troponin ([TCa*]+[T*]). (C) Half sarcomere length. (D) Cross-bridge-generated contraction force (CBCF). (E) LV pressure according to arterial stiffness. Here, En represents the normal stiffness value of the large arteries.
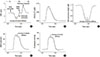
Fig. 6
Simulation results of the (A) peak cellular stress of the ventricle, (B) pulse wave velocity (PWV) change, (C) brachial and central systolic blood pressures (SBP) with respect to arterial stiffness, and (D) peak cellular stress with respect to PWV.

Notes
References
1. Abhayaratna WP, Barnes ME, O'Rourke MF, Gersh BJ, Seward JB, Miyasaka Y, Bailey KR, Tsang TS. Relation of arterial stiffness to left ventricular diastolic function and cardiovascular risk prediction in patients > or =65 years of age. Am J Cardiol. 2006; 98:1387–1392.
2. Urbina EM, Dolan LM, McCoy CE, Khoury PR, Daniels SR, Kimball TR. Relationship between elevated arterial stiffness and increased left ventricular mass in adolescents and young adults. J Pediatr. 2011; 158:715–721.
3. Kerckhoffs RC, Neal ML, Gu Q, Bassingthwaighte JB, Omens JH, McCulloch AD. Coupling of a 3D finite element model of cardiac ventricular mechanics to lumped systems models of the systemic and pulmonic circulation. Ann Biomed Eng. 2007; 35:1–18.
4. Lim KM, Lee JS, Song JH, Youn CH, Choi JS, Shim EB. Theoretical estimation of cannulation methods for left ventricular assist device support as a bridge to recovery. J Korean Med Sci. 2011; 26:1591–1598.
5. Trayanova NA, Rice JJ. Cardiac electromechanical models: from cell to organ. Front Physiol. 2011; 2:43.
6. Campbell SG, McCulloch AD. Multi-scale computational models of familial hypertrophic cardiomyopathy: genotype to phenotype. J R Soc Interface. 2011; 8:1550–1561.
7. Shim EB, Sah JY, Youn CH. Mathematical modeling of cardiovascular system dynamics using a lumped parameter method. Jpn J Physiol. 2004; 54:545–553.
8. Shim EB, Leem CH, Abe Y, Noma A. A new multi-scale simulation model of the circulation: from cells to system. Philos Trans A Math Phys Eng Sci. 2006; 364:1483–1500.
9. Shim EB, Amano A, Takahata T, Shimayoshi T, Noma A. The cross-bridge dynamics during ventricular contraction predicted by coupling the cardiac cell model with a circulation model. J Physiol Sci. 2007; 57:275–285.
10. Shim EB, Jun HM, Leem CH, Matusuoka S, Noma A. A new integrated method for analyzing heart mechanics using a cell-hemodynamics-autonomic nerve control coupled model of the cardiovascular system. Prog Biophys Mol Biol. 2008; 96:44–59.
11. Ozawa ET, Bottom KE, Xiao X, Kamm RD. Numerical simulation of enhanced external counterpulsation. Ann Biomed Eng. 2001; 29:284–297.
12. Stettler JC, Niederer P, Anliker M. Theoretical analysis of arterial hemodynamics including the influence of bifurcations: part I: mathematical models and prediction of normal pulse patterns. Ann Biomed Eng. 1981; 9:145–164.
13. Avolio AP. Multi-branched model of the human arterial system. Med Biol Eng Comput. 1980; 18:709–718.
14. Dell'Italia LJ, Walsh RA. Application of a time varying elastance model right ventricular performance in man. Cardiovasc Res. 1988; 22:864–874.
15. Negroni JA, Lascano EC. A cardiac muscle model relating sarcomere dynamics to calcium kinetics. J Mol Cell Cardiol. 1996; 28:915–929.
16. Nygren A, Fiset C, Firek L, Clark JW, Lindblad DS, Clark RB, Giles WR. Mathematical model of an adult human atrial cell: the role of K+ currents in repolarization. Circ Res. 1998; 82:63–81.
17. ten Tusscher KH, Noble D, Noble PJ, Panfilov AV. A model for human ventricular tissue. Am J Physiol Heart Circ Physiol. 2004; 286:H1573–H1589.
18. Matsuoka S, Sarai N, Kuratomi S, Ono K, Noma A. Role of individual ionic current systems in ventricular cells hypothesized by a model study. Jpn J Physiol. 2003; 53:105–123.
19. Heldt T, Shim EB, Kamm RD, Mark RG. Computational modeling of cardiovascular response to orthostatic stress. J Appl Physiol. 2002; 92:1239–1254.
20. Avolio AP. Multi-branched model of the human arterial system. Med Biol Eng Comput. 1980; 18:709–718.
21. Izzo JL Jr, Shykoff BE. Arterial stiffness: clinical relevance, measurement, and treatment. Rev Cardiovasc Med. 2001; 2:29–34.
22. Gozna ER, Marble AE, Shaw AJ, Winter DA. Mechanical properties of the ascending thoracic aorta of man. Cardiovasc Res. 1973; 7:261–265.
23. Lehmann ED, Parker JR, Hopkins KD, Taylor MG, Gosling RG. Validation and reproducibility of pressure-corrected aortic distensibility measurements using pulse-wave-velocity Doppler ultrasound. J Biomed Eng. 1993; 15:221–228.
24. Stewart AD, Millasseau SC, Kearney MT, Ritter JM, Chowienczyk PJ. Effects of inhibition of basal nitric oxide synthesis on carotid-femoral pulse wave velocity and augmentation index in humans. Hypertension. 2003; 42:915–918.
25. Roman MJ, Devereux RB, Kizer JR, Okin PM, Lee ET, Wang W, Umans JG, Calhoun D, Howard BV. High central pulse pressure is independently associated with adverse cardiovascular outcome the strong heart study. J Am Coll Cardiol. 2009; 54:1730–1734.
26. Wang KL, Cheng HM, Chuang SY, Spurgeon HA, Ting CT, Lakatta EG, Yin FC, Chou P, Chen CH. Central or peripheral systolic or pulse pressure: which best relates to target organs and future mortality? J Hypertens. 2009; 27:461–467.
27. Rochette L, Tatou E, Maupoil V, Zeller M, Cottin Y, Jazayeri S, Brenot R, Girard C, David M, Vergely C. Atrial and vascular oxidative stress in patients with heart failure. Cell Physiol Biochem. 2011; 27:497–502.
28. Kashif FM, Verghese GC, Novak V, Czosnyka M, Heldt T. Model-based noninvasive estimation of intracranial pressure from cerebral blood flow velocity and arterial pressure. Sci Transl Med. 2012; 4:129ra44.
29. Landesberg A, Sideman S. Mechanical regulation of cardiac muscle by coupling calcium kinetics with cross-bridge cycling: a dynamic model. Am J Physiol. 1994; 267:H779–H795.
30. Beyar R, Sideman S. Atrioventricular interactions: a theoretical simulation study. Am J Physiol. 1987; 252:H653–H665.
31. Ursino M, Innocenti M. Modeling arterial hypotension during hemodialysis. Artif Organs. 1997; 21:873–890.




 PDF
PDF ePub
ePub Citation
Citation Print
Print






 XML Download
XML Download