Comparison of Formulas for Calculating Low-density Lipoprotein Cholesterol in General Population and High-risk Patients with Cardiovascular Disease

Hansol Choi; Jee-Seon Shim; Myung Ha Lee; Young Mi Yoon; Dong Phil Choi; Hyeon Chang Kim

doi:10.4070/kcj.2016.46.5.688

Journal List > Korean Circ J > v.46(5) > 1017398

Go to TopGo to Top Go to BottomGo to Bottom

TOOLS

Choi, Shim, Lee, Yoon, Choi, and Kim: Comparison of Formulas for Calculating Low-density Lipoprotein Cholesterol in General Population and High-risk Patients with Cardiovascular Disease

Original Article

Korean Circulation Journal 2016; 46(5): 688-698.

Published online: 28 September 2016

DOI: https://doi.org/10.4070/kcj.2016.46.5.688

Comparison of Formulas for Calculating Low-density Lipoprotein Cholesterol in General Population and High-risk Patients with Cardiovascular Disease

Hansol Choi, MPH^1,³, Jee-Seon Shim, PhD³, Myung Ha Lee, PhD^2,³, Young Mi Yoon, MS³, Dong Phil Choi, PhD³, Hyeon Chang Kim, MD^2,³

¹Department of Public Health, Yonsei University Graduate School, Seoul, Korea.

²Department of Preventive Medicine, Yonsei University College of Medicine, Seoul, Korea.

³Cardiovascular and Metabolic Disease Etiology Research Center, Yonsei University College of Medicine, Seoul, Korea.

Correspondence: Hyeon Chang Kim, MD, Department of Preventive Medicine, Yonsei University College of Medicine, 50-1 Yonsei-ro, Seodaemun-gu, Seoul 03722, Korea. Tel: 82-2-2228-1873; Fax: 82-2-392-8133, hckim@yuhs.ac

Received 22 September 2015 Revised 22 December 2015 Accepted 3 May 2016

(open-access):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Background and Objectives

Low-density lipoprotein cholesterol (LDL-C), an established cardiovascular risk factor, can be generally determined by calculation from total cholesterol, high-density lipoprotein cholesterol, and triglyceride concentrations. The aim of this study was to compare LDL-C estimations using various formulas with directly measured LDL-C in a community-based group and hospital-based group among the Korean population.

Subjects and Methods

A total of 1498 participants were classified into four groups according to triglyceride concentrations as follows: <100, 100–199, 200–299, and ≥300 mg/dL. LDL-C was calculated using the Friedewald, Chen, Vujovic, Hattori, de Cordova, and Anandaraja formulas and directly measured using a homogenous enzymatic method. Pearson's correlation coefficients, intraclass correlation coefficients (ICC), Passing & Bablok regression, and Bland-Altman plots were used to evaluate the performance of six formulas.

Results

The Friedewald formula had the highest accuracy (ICC=0.977; 95% confidence interval 0.974-0.979) of all the triglyceride ranges, while the Vujovic formula had the highest accuracy (ICC=0.876; 98.75% confidence interval 0.668–0.951) in people with triglycerides ≥300 mg/dL. The mean difference was the lowest for the Friedewald formula (0.5 mg/dL) and the percentage error was the lowest for the Vujovic formula (30.2%). However, underestimation of the LDL-C formulas increased with triglyceride concentrations.

Conclusion

The accuracy of the LDL-C formulas varied considerably with differences in triglyceride concentrations. The Friedewald formula outperformed other formulas for estimating LDL-C against a direct measurement and the Vujovic formula was suitable for hypertriglyceridemic samples; it could be used as an alternative cost-effective tool to measure LDL-C when the direct measurement cannot be afforded.

Keywords: Low-density lipoprotein cholesterol, Cholesterol, Triglyceride, Friedewald formula

Introduction

Low-density lipoprotein cholesterol (LDL-C) is an important modifiable risk factor for cardiovascular disease (CVD). LDL-C is recognized as the primary target of therapy in clinical practice guidelines including in the United States, Europe, and Korea.1)2)3) LDL-C is the most appropriate factor for patient classification in risk management of CVD, highlighting the comprehensive understanding of the need for accurate and precise LDL-C estimation. The accepted gold standard or reference method for LDL-C estimation is β-quantification after ultracentrifugation,4) which is not commonly affordable as it is labor-intensive, time-consuming, and expensive.5) Recently, direct homogeneous assays for measurement of LDL-C have been developed and have shown reasonable accuracy and precision when compared with the reference method.6)

Several formulas have been developed to estimate LDL-C.5)7)8)9)10)11) Of these, the most generally used formula worldwide to calculate LDL-C is the Friedewald formula and it is accepted as an accurate and cost-effective alternative to direct measurement.9) However, it cannot be applied when the fasting serum triglyceride (TG) concentrations are above 400 mg/dL, due to the underestimation and lack of concordance with the direct measurement of LDL-C. Since Scharnagl et al. first reported the underestimation of the Friedewald formula,12) a number of other studies have described the underestimation and inaccuracy of the Friedewald formula, especially in extreme lipid values and with comorbidities.7)8)12)13)14)15)16)17) Most alternative formulas have been developed using multivariate linear regression analysis with LDL-C as a dependent variable and total cholesterol (TC), high-density lipoprotein cholesterol (HDL-C), and TG as independent variables.7)8)9)10)11)18) Unlike the other formulas, the Anandaraja formula was developed in order to calculate LDL-C without using HDL-C as an independent variable.5) However, all of these LDL-C formulas have had varying results in different populations or have performed more poorly than the Friedewald formula. Although such various LDL-C formulas have been developed, only a small number of studies have compared them.13)14)15)16)17) LDL-C can be measured to identify high-risk individuals in the mass screening, as well as to assess an individual's cardiovascular risk among known high risk patients.1)2)3)4)19) However, previous studies have not separately compared the accuracy of calculated LDL-C in both the general population and in high-risk patients of CVD. Therefore, in this study, we assessed the performance of six LDL-C formulas (Friedewald, de Cordova, Vujovic, Chen, Hattori, and Anandaraja) by comparing them with the direct measurement of LDL-C in the general population from the community-based group and the high-risk patients of CVD from the hospital-based group.

Subjects and Methods

Study population

Data for the present study were derived from the Cardiovascular and Metabolic Disease Etiology Research Center (CMERC) study, an ongoing prospective cohort study. The CMERC study consists of the community-based group from the general population and the hospital-based group from the patients at high risk of CVD. As shown in Fig. 1, initially 2163 participants were enrolled into this study. However, to calculate LDL-C using the formulas, we limited our main analysis to participants whose TC, TG, HDL-C, and LDL-C were all measured and whose TG concentrations were 400 mg/dL or less. After excluding a total of 665 participants (596 participants with unmeasured directly-measured LDL-C, 45 participant with missing value of serum lipids, and 24 participants with TG concentration more than 400 mg/dL), a current cross-sectional analysis was conducted for a total of 1498 participants who were recruited from either the community-based group (n=1051) or the hospital-based group (n=447). In addition, a sensitivity analysis including 24 additional people with TG concentration more than 400 mg/dL, was also conducted. The community-based group included a free-living general population residing in four districts throughout South Korea (Seoul, Goyang, Gimpo, and Incheon). Eligibility criteria for each inclusion participant comprised of being in the age range of 30 to 64 years, having lived more than eight months of the year at their current residence with no migration plans over the next two years, and ability to provide verbal or written consent to participate in the study. Participants were excluded if they were diagnosed with cancer within the last two years or were currently being treated for cancer, had a history of myocardial infarction, stroke, or heart failure, were currently involved in pharmaceutical trials, and were currently pregnant or reported the possibility of being pregnant on the day of registration. The hospital-based group was recruited from the cardiology outpatient department at Severance hospital, Yonsei University. This study group was registered with ClinicalTrials.gov under the identifier number NCT02003781 (http://www.clinicaltirals.gov). The hospital-based group included patients having conditions known for significantly increased risks of CVD: hypertension with subclinical target organ damage, type 2 diabetes with microalbuminuria, chronic kidney disease with dialysis or transplant, rheumatoid arthritis and on medication, subclinical peripheral vascular disease, atrial fibrillation, and immediate family members who were myocardial infarction patients. All participants provided written informed consent, and the Institutional Review Board of Severance Hospital, Yonsei University College of Medicine, approved the study protocol.

Measurements

Fasting blood samples were collected from the antecubital vein after fasting for at least 8 hours. For the community-based group, blood samples were sent to an independent research laboratory center for analysis. Serum concentrations of TC, TG, HDL-C, and LDL-C were measured using enzymatic methods with an automatic analyzer (ADVIA 1800, Siemens, Tarrytown, NY, USA). The coefficients of variation were 0.5-0.8% for TC, 2.0-2.6% for HDL-C, 2.8-2.9% for LDL-C, and 0.9-2.4% for TG. In the hospital-based group, serum concentrations of TC, HDL-C, LDL-C, and TG were measured using enzymatic methods with an automatic analyzer (Hitachi 7600 DDP, Hitachi High-Technologies, Tokyo, Japan). The coefficients of variation were 0.8-0.9% for TC, 18.3-18.4% for HDL-C, 1.0-1.2% for LDL-C, and 1.0-1.2% for TG.

In addition to direct measurement, LDL-C was calculated according to the following formulas:

• Friedewald9): LDL-C=TC-HDL-C-(TG/5)

• Hattori10): LDL-C=(0.94×TC)-(0.94×HDL-C)-(0.19×TG)

• Anandaraja5): LDL-C=(0.9×TC)-(0.9×TG/5)-28

• Vujovic11): LDL-C=TC-HDL-C-(TG/6.58)

• Chen7): LDL-C=(TC-HDL-C)×0.9-(TG×0.1)

• de Cordova8): LDL-C=0.7516×(TC-HDL-C)

Statistical analysis

We performed statistical analyses for all participants and for each of the two groups. In addition, participants were classified into four groups according to serum TG concentration as follows: <100, 100-199, 200-299, and ≥300 mg/dL. In addition, sensitivity analysis was carried out when the serum TG concentration was more than 400 mg/dL. The performance of all estimated formulas was compared at different concentrations of TG. To test for a normal distribution, the Q-Q plot (as shown in Supplementary Fig. 1, 2, and 3), Kolmogorov-Smirnov with the Lilliefors significance correction, skewness, and kurtosis were used. The distribution of continuous variables were described as means with standard deviations (for normally distributed variables) or as a median with an interquartile range (for skewed variables) and compared using an independent t-test and Wilcoxon rank sum test, respectively. Categorical variables are reported as observed numbers and percentages; these were compared using the chi-square test. Correlation between LDL-C by estimated formulas and by direct measurement was calculated using the Pearson's correlation. The intraclass correlation coefficient (ICC) analysis was performed in order to evaluate the degree of absolute agreement between the estimated and directly measured LDL-C. For the purpose of multiple subdivision analyses, ICC for all of serum TG ranges had a 95% confidence interval (CI); ICC for each partial TG ranges had 98.75% CI. In addition, we compared the performance of ICC only for all of the serum TG ranges divided into a community-based group and a hospital-based group since the correction of multiple comparisons. We also used the graphical procedure outlined by Bland-Altman plots and Passing & Bablok regression equation. Agreement between the two measurements was tested by calculating systematic errors (bias), and 95% limits of agreement (LOA) as bias±2 standard deviations as described by Bland-Altman plots.20) The percentage error is derived by dividing the limits of agreement by the mean value of the measurements obtained with the established method.21) Passing and Bablok regression analyses are statistical procedures that allow valuable estimations of analytical method agreements and possible systematic bias, expressed in the equation by y=a+bx, where a is the intercept of the line (representing the constant error) and b is the slope in the y axis (representing the proportional error).22)23) If 0 is not in the 95% CI of the intercept there is a constant difference and if 1 is not in the 95% CI of the slope then there is a proportional difference between the two methods.23) In addition, the Cusum test for linearity was used to evaluate how well a linear model fits the data in the Passing and Bablok methods.

All statistical analyses were performed using SAS software (version 9.2, SAS, Cary, NC, USA), SPSS software (version 23, IBM SPSS Inc., Chicago, IL, USA), and MedCalc software (version 15.4, MedCalc, Ostend, Belgium). Statistical significance was defined as a two-sided p-value of less than 0.05.

Results

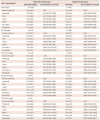
The general characteristics of the participants are presented in Table 1. A total of 1498 lipid profiles were identified, of which 654 (43.7%) were male and 844 (56.3%) were female. The median age of the participants was 53 years, and the community-based group was found to be younger than the hospital-based group. TC ranged from 93.0 to 337.0 mg/dL with a mean of 189.2 mg/dL; TG ranged from 16.0 to 392.0 mg/dL with a median of 104.0 mg/dL; HDL-C ranged from 17.0 to 124.0 mg/dL with a median of 53.0 mg/dL; and directly-measured LDL-C ranged from 33.0 to 246.0 mg/dL with a mean of 110.7 mg/dL. Of the various formulas, the De Cordova formula produced the lowest mean (103.4 mg/dL), and the Anandaraja formula produced the highest mean (101.0 mg/dL). The mean values of LDL-C were significantly higher in the community-based group than in the hospital-based group, likely due to the difference in the frequency of lipid-lowering drugs (8.8% and 54.8%, respectively). The prevalence of known chronic disorders and medications for these diseases were higher in the hospital-based group than in the community-based group.

Table 2 compared estimated LDL-C using the six formulas to directly measured LDL-C according to TG concentration. Along with the increase of TG concentration, the difference between calculated LDL-C and measured LDL-C also increased. As a further visual cue, Supplementary Fig. 4 shows the correlation of directly-measured LDL-C with estimated LDL-C. The ICC between the estimated and directly-measured LDL-C was significantly higher with the Friedewald formula (ICC=0.977; 95% CI: 0.974–0.979) for all serum TG ranges compared with the Chen formula (ICC=0.973; 95% CI: 0.969–0.977; p-value 0.008), the Vujovic formula (ICC=0.972; 95% CI: 0.934–0.985; p-value<0.001), the Hattori formula (ICC=0.961; 95% CI: 0.849–0.983; p-value<0.001), the de Cordova formula (ICC=0.916; 95% CI: 0.734–0.960; p-value<0.001), and the Anandaraja formula (ICC=0.901; 95% CI: 0.787–0.943; p-value<0.001). At the low end of the TG range, the Friedewald formula seemed to have better accuracy with an ICC of 0.980 (98.75% CI=0.974–0.984). At the high end of the TG range, the Vujovic formula showed higher accuracy with an ICC of 0.876 (98.75% CI=0.668–0.951) compared with other formulas. However, as shown in Supplementary Fig. 5, the accuracy of the formulas have declined as the serum TG concentration increases.

We also performed the comparison analysis separately for both the community-based group and the hospital-based group in Table 3, and the results were quite consistent. At all of the TG ranges, the Friedewald formula had a significantly higher accuracy with an ICC of 0.976 (95% CI 0.973–0.979) compared with the Hattori formula (ICC=0.955; 95% CI: 0.754–0.982; p-value<0.001), the de Cordova formula (ICC=0.904; 95% CI: 0.488–0.963; p-value<0.001) and the Anandaraja formula (ICC=0.888; 95% CI: 0.741–0.939; p-value<0.001) in the community-based group and with an ICC of 0.973 (95% CI 0.967–0.978) compared with the Vujovic formula (ICC=0.959; 95% CI: 0.812–0.983; p-value<0.001), the de Cordova formula (ICC=0.932; 95% CI: 0.908–0.948; p-value<0.001), and the Anandaraja formula (ICC=0.898; 95% CI: 0.817–0.936; p-value<0.001) in the hospital-based group, respectively. At the low end of the TG ranges, the Friedewald formula showed a relatively higher accuracy with an ICC of 0.985 (98.75% CI=0.981–0.988) in the community-based group, while the Chen formula showed a higher accuracy with an ICC of 0.962 (98.75% CI=0.945–0.974) in the hospital-based group. At the high end of the TG ranges, the Vujovic formula showed better accuracy with an ICC of 0.893 (98.75% CI=0.677–0.965) in the community-based group, and the Anandaraja formula had better accuracy with an ICC of 0.927 (98.75% CI=0.604–0.987) in the hospital-based group. An additional comparison analysis was conducted as a sensitivity analysis to assess the effect of including 24 participants with TG concentrations is more than 400 mg/dL shown in Supplementary Table 1. The Vujovic formula seemed to have a higher accuracy in both the community-based group and the hospital-based group with an ICC of 0.569 (95% CI -0.276–0.855) and 0.873 (95% CI 0.460–0.971) compared with other formulas, respectively. However, as shown in Supplementary Table 2, all of the estimated formulas became inaccurate, especially when the TG concentrations exceeded 1000 mg/dL.

Fig. 2 presents the mean differences of the estimated formulas against directly measured LDL-C in the Bland-Altman plots in the overall population. The mean difference (measured LDL-C –estimated LDL-C) represents the estimation of bias between the two observations. The mean bias was the lowest for the Friedewald formula (0.5 mg/dL, limits of agreement -17.8 and 18.8), followed by the Chen formula (1.8 mg/dL, limits of agreement -16.6 and 20.3), the Vujovic formula (-5.3 mg/dL, limits of agreement -22.8 and 12.2), the Hattori formula (7.3 mg/dL, limits of agreement -11.0 and 25.7), the De Cordova formula (9.7 mg/dL, limits of agreement -15.9 and 35.3), and the Anandaraja formula (–9.8 mg/dL, limits of agreement -42.6 and 23.0). The percentage error was the lowest for the Vujovic formula (30.2%), followed by the Friedewald formula (33.2%), the Chen formula (33.9%), Hattori formula (35.5%), De Cordova formula (50.7%), and lastly the Anandaraja formula (54.4%). Fig. 3 showed the reliability of different methods for measuring LDL-C using the Passing & Bablok linear regression analysis. As shown in Supplementary Table 3, calculation of the slope and the intercept in each formula against for directly measured LDL-C shows that the Friedewald formula indicated good agreement without both constant and proportional bias.

Discussion

Since the release of the first the National Cholesterol Education Program Adult Treatment Panel guidelines in 1988, LDL-C has been focused on therapeutic decision-making and the efficacy of medical intervention.19) It is essential to accurately estimate LDL-C, as it has significant implications on cardiovascular risk stratification and can affect therapy and outcomes.14) Over the last 40 years, the Friedewald formula has been used the most widely to estimate LDL-C in clinical practice as well as in health screenings. To improve its accuracy and reliability, several modified formulas have been suggested. However, these modifications were not found to be suitable replacements of the Friedewald formula.

In the present study, we compared Friedewald formula (developed in 1972) and other five relatively new formulas (developed in 1998-2013) against directly measured LDL-C in a Korean population. Overall, there were good correlations between estimated LDL-C and measured LDL-C. Among the six formulas, the Friedewald formula showed the best performance for estimating LDL-C (ICC=0.977; 95% CI 0.974–0.979), and there was only a small mean difference (0.5 mg/dL) compared to the directly-measured LDL-C without both a constant and proportional bias. These results showed a similar tendency in each of the different groups divided according to cardiovascular risk. However, when the serum TG concentrations exceeded 400 mg/dL, the Vujovic formula performed well in both the community-based group and the hospital-based group.

As in previous studies, of all clinical parameters, serum TG concentration was the most significant contributor in determining the difference between directly-measured LDL-C and estimated LDL-C.24)25)26) The differences between directly measured LDL-C and estimated LDL-C were related to TG concentration, as it was also shown in this study that underestimation of LDL-C increased with the concentration of TG.24)25)26) Results of the study were consistent with previous studies, indicating that the Friedewald formula performs poorly when TG concentrations are very high.7)8)14)16)17)24)

The present study also had several limitations that need to be addressed. First, the β-quantification method was not used, which is considered the gold standard method for measuring LDL-C. Instead, LDL-C was measured using the enzymatic method, which had an assay precision within the NCEP performance guidelines, producing a total error rate of ≤12%, an accuracy rate of ±4%, and a CV rate ≤4%.4)27) Second, taking only a single measurement of LDL-C may have resulted in misclassification of the participants. Despite being commonly used in clinical decision-making, most of the guidelines suggested sequential measurements to improve the accuracy and precision of LDL-C with intervention. In addition, direct comparison was limited, as the lipid measurement methods differed between the community-based group and the hospital-based group. A different method of evaluation of the directly measured LDL-C could lead to misclassification of the outcome. However, the effects of non-differential misclassification would have resulted in a bias toward null. Finally, based on the exclusion criteria, a bias in the selection of participants is possible. In addition, we did not exclude participants who were taking statins or other lipid-modifying agents, which could have affected results.

In conclusion, most of the LDL-C formulas correlated well with directly-measured LDL-C overall, especially at a serum TG concentration of <300 mg/dL. Among the six LDL-C formulas, the Friedewald formula showed the best performance for estimating LDL-C, while the Vujovic formula showed a higher accuracy in people with TG ≥300 mg/dL compared with other formulas. Results indicated that the Friedewald formula could be used as an alternative cost-effective tool to measure LDL-C when a direct measurement cannot be afforded or accuracy is not crucial. In addition, the Vujovic formula could be used instead of Friedewald formula for the estimation of LDL-C in participants with serum TG concentrations is greater than 400 mg/dL, which is well known as the limitation of Friedewald formula. However, with the hypertriglyceridemic samples, the LDL-C calculation obtained from LDL-C formulas exhibited the poorer accuracy, which could affect clinical decision-making.

Figures and Tables

Fig. 1

Flow chart of study participants. LDL-C: low-density lipoprotein cholesterol, TG: triglycerides.

Fig. 2

Bland-Altman plots of estimated formulas against directly-measured LDL-C. The mean difference represents the estimation of bias between the two observations and the percentage error represents the proportion between the magnitude of measurement and error in measurement. LDL-C: low-density lipoprotein cholesterol.

Fig. 3

Passing & Bablok regression of estimated formulas against directly-measured LDL-C. The dotted line represents the line of identity. No significant deviation from linearity. LDL-C: low-density lipoprotein cholesterol.

Table 1

General characteristics of study participants (n=1498)

Variables	Total (n=1498)	Population-based cohort (n=1051)	Hospital-based cohort (n=447)	p
Age, years	53.0 [41.0–60.0]	50.0 [37.0–56.0]	61.0 [53.0–68.0]	<0.001
Sex, n(%)
Men	654 (43.7)	409 (38.9)	245 (54.8)	<0.001
Women	844 (56.3)	642 (61.1)	202 (45.2)	<0.001
Body mass index, kg/m²	24.1±3.4	23.6±3.2	25.4±3.6	<0.001
Total cholesterol, mg/dL	189.2±35.2	195.8±34.3	173.7±32.4	<0.001
Triglycerides, mg/dL	104.0 [76.0–149.0]	101.0 [74.0–145.0]	111.0 [80.0–163.0]	0.004
HDL-C, mg/dL	53.0 [44.0–62.0]	55.0 [47.0–66.0]	48.0 [41.0–56.0]	<0.001
LDL-C, mg/dL
Directly-measured, mg/dL	110.7±31.3	116.4±30.6	97.5±28.9	<0.001
Friedewald, mg/dL	110.3±31.0	115.0±30.4	99.0±29.4	<0.001
Chen, mg/dL	108.9±28.3	113.0 ± 28.0	99.3±26.7	<0.001
Vujovic, mg/dL	116.1±31.1	120.7±30.6	105.1±29.4	<0.001
Hattori, mg/dL	103.4±29.1	107.9±28.5	92.8±27.7	<0.001
De Cordova, mg/dL	101.0±25.1	104.2±25.0	93.5±23.7	<0.001
Anandaraja, mg/dL	120.6±31.6	127.0±30.5	105.5±29.2	<0.001
Previously known diseases, n(%)
Hypertension	487 (32.5)	142 (13.5)	345 (77.2)	<0.001
Diabetes mellitus	148 (9.9)	39 (3.7)	109 (24.4)	<0.001
Dyslipidemia	313 (20.9)	156 (14.8)	157 (35.1)	<0.001
Medication history, n(%)
Antihypertensive drug	474 (31.6)	128 (12.2)	346 (77.4)	<0.001
Antidiabetic drug	128 (8.5)	35 (3.3)	93 (20.8)	<0.001
Lipid lowering drug	337 (22.5)	92 (8.8)	245 (54.8)	<0.001

Data expressed as a mean±standard deviation for normal distribution, median [interquartile range] for non-normal distribution, or number (percent) for categorical variables. HDL-C: high-density lipoprotein cholesterol, LDL-C: low-density lipoprotein cholesterol

Table 2

Comparison of estimated formulas to directly-measured LDL-C according to serum TG concentration (TG ≤400 mg/dL)

LDL-C measurement	Mean±SD (mg/dL)	Mean difference	ICC (confidence interval)^*
All TG ranges (n=1498)
Directly-measured	110.7±31.3	NA	1.000
Friedewald	110.3±31.0	0.5	0.977 (0.974–0.979)
Chen	108.9±28.3	1.8	0.973 (0.969–0.977)
Vujovic	116.1±31.1	−5.3	0.972 (0.934–0.985)
Hattori	103.4±29.1	7.3	0.961 (0.849–0.983)
De Cordova	101.0±25.1	9.7	0.916 (0.734–0.960)
Anandaraja	120.6±31.6	−9.8	0.901 (0.787–0.943)
TG<100 mg/dL (n=697)
Directly-measured	106.0±29.5	NA	1.000
Friedewald	107.7±29.4	−1.7	0.980 (0.974–0.984)
Chen	102.7±26.7	3.3	0.975 (0.957–0.984)
Vujovic	111.1±29.5	−5.2	0.973 (0.903–0.988)
Hattori	101.1±27.6	4.9	0.972 (0.910–0.987)
De Cordova	91.8±22.7	14.1	0.896 (−0.268–0.976)
Anandaraja	123.4±30.1	−17.5	0.843 (−0.129–0.953)
TG 100–199 mg/dL (n=623)
Directly-measured	116.5±32.5	NA	1.000
Friedewald	115.0±32.4	1.4	0.981 (0.976–0.985)
Chen	114.5±29.1	2.0	0.976 (0.969–0.981)
Vujovic	121.6±32.4	−5.1	0.975 (0.922–0.988)
Hattori	107.9±30.4	8.6	0.960 (0.638–0.988)
De Cordova	107.0±24.5	9.4	0.930 (0.641–0.974)
Anandaraja	121.6±32.6	−5.1	0.946 (0.912–0.965)
TG 200–299 mg/dL (n=145)
Directly-measured	110.0±31.8	NA	1.000
Friedewald	105.2±30.1	4.8	0.957 (0.915–0.976)
Chen	113.3±26.8	−3.3	0.952 (0.923–0.970)
Vujovic	116.4±29.9	−6.4	0.952 (0.869–0.977)
Hattori	98.4±28.3	11.6	0.925 (0.278–0.979)
De Cordova	114.1±22.3	−4.1	0.920 (0.870–0.949)
Anandaraja	107.6±30.2	2.4	0.957 (0.933–0.972)
TG 300–399 mg/dL (n=33)
Directly-measured	106.1±27.5	NA	1.000
Friedewald	96.9±27.0	9.2	0.862 (0.575–0.950)
Chen	114.4±24.4	−8.3	0.865 (0.600–0.950)
Vujovic	113.3±27.0	−7.1	0.876 (0.668–0.951)
Hattori	90.4±25.4	15.7	0.809 (−0.071–0.947)
De Cordova	124.0±20.6	−17.9	0.757 (−0.309–0.937)
Anandaraja	97.1±27.9	9.0	0.852 (0.576–0.944)

The mean difference (directly-measured LDL-C – estimated LDL-C) represents the estimation of bias between the two observations. ^*ICC (95% confidence interval) for all TG ranges and ICC (98.75% confidence interval) for each partial TG ranges. LDL-C: low-density lipoprotein cholesterol, TG: triglycerides, SD: standard deviation, ICC: intraclass correlation coefficient, NA: not applicable

Table 3

Cohort-specific comparison of estimated formulas to directly-measured LDL-C according to serum TG concentration (TG ≤400 mg/dL)

LDL-C measurement	Community-based group		Hospital-based group
LDL-C measurement	Mean±SD (mg/dL)	ICC (confidence interval)^†	Mean±SD	ICC (confidence interval)^*
All TG ranges	(n=1051)		(n=447)
Directly-measured	116.4±30.6	1.000	97.5±28.9	1.000
Friedewald	115.0±30.4	0.976 (0.973–0.979)	99.0±29.4	0.973 (0.967–0.978)
Chen	113.0±28.0	0.972 (0.959–0.980)	99.3±26.7	0.970 (0.963–0.976)
Vujovic	120.7±30.6	0.974 (0.952–0.984)	105.1±29.4	0.959 (0.812–0.983)
Hattori	107.9±28.5	0.955 (0.754–0.982)	92.8±27.7	0.966 (0.934–0.980)
De Cordova	104.2±25.0	0.904 (0.488–0.963)	93.5±23.7	0.932 (0.908–0.948)
Anandaraja	127.0±30.5	0.888 (0.741–0.939)	105.5±29.2	0.898 (0.817–0.936)
TG<100 mg/dL	(n=513)		(n=184)
Directly-measured	110.0±29.3	1.000	94.6±27.3	1.000
Friedewald	110.8±29.3	0.985 (0.981–0.988)	98.9±27.9	0.953 (0.920–0.971)
Chen	105.5±26.7	0.977 (0.919–0.990)	94.9±25.3	0.962 (0.945–0.974)
Vujovic	114.3±29.5	0.980 (0.936–0.991)	102.4±28.0	0.947 (0.684–0.981)
Hattori	104.0±27.5	0.973 (0.790–0.991)	92.8±26.2	0.962 (0.945–0.974)
De Cordova	94.2±22.8	0.885 (−0.270–0.976)	85.3±21.4	0.914 (0.512–0.970)
Anandaraja	128.0±29.7	0.842 (−0.210–0.956)	110.8±27.6	0.805 (0.029–0.933)
TG 100–199 mg/dL	(n=422)		(n=201)
Directly-measured	123.9±30.8	1.000	100.9±30.3	1.000
Friedewald	121.7±30.9	0.978 (0.968–0.984)	101.1±31.0	0.982 (0.974–0.987)
Chen	120.4±27.8	0.971 (0.953–0.981)	102.1±27.9	0.979 (0.970–0.985)
Vujovic	128.2±30.9	0.973 (0.939–0.986)	107.7±31.0	0.969 (0.767–0.990)
Hattori	114.1±29.1	0.949 (0.442–0.985)	94.7±29.1	0.971 (0.831–0.990)
De Cordova	111.9±23.4	0.909 (0.197–0.973)	96.8±23.5	0.954 (0.918–0.972)
Anandaraja	129.8±30.8	0.932 (0.878–0.958)	104.3±29.6	0.955 (0.930–0.970)
TG 200–299 mg/dL	(n=94)		(n=51)
Directly-measured	118.6±29.5	1.000	94.2±30.3	1.000
Friedewald	112.3±28.0	0.933 (0.841–0.967)	92.1±29.5	0.983 (0.965–0.992)
Chen	119.7±25.1	0.935 (0.891–0.962)	101.6±26.2	0.963 (0.607–0.990)
Vujovic	123.5± 27.9	0.936 (0.876–0.965)	103.4±29.3	0.962 (0.114–0.992)
Hattori	105.1± 26.3	0.888 (0.036–0.969)	86.1±27.8	0.964 (0.408–0.991)
De Cordova	119.4± 21.0	0.905 (0.840–0.944)	104.5±21.6	0.917 (0.327–0.977)
Anandaraja	115.4±27.5	0.942 (0.900–0.966)	93.2±30.1	0.964 (0.925–0.982)
TG 300–399 mg/dL	(n=22)		(n=11)
Directly-measured	110.2±30.7	1.000	97.9±17.9	1.000
Friedewald	98.4±29.6	0.859 (0.419–0.959)	93.9±21.8	0.882 (0.395–0.978)
Chen	116.2±26.2	0.886 (−0.652–0.963)	110.9±20.8	0.778 (−0.382–0.964)
Vujovic	115.0±29.3	0.893 (0.677–0.965)	109.7±22.5	0.802 (−0.239–0.967)
Hattori	91.8±27.8	0.805 (−0.213–0.954)	87.6±20.4	0.830 (−0.150–0.972)
De Cordova	125.9±21.6	0.801 (−0.087–0.950)	120.1±18.8	0.600 (−0.337–0.934)

^*ICC (95% confidence interval) for all TG ranges and ICC (98.75% confidence interval) for each partial TG ranges. LDL-C: low-density lipoprotein cholesterol, TG: triglycerides, SD: standard deviation, ICC: intraclass correlation coefficient, NA: not applicable

Acknowledgments

This work was supported by the Research Program funded by the Korean Health Technology R&D Project, Ministry of Health & Welfare (HI13C0715).

Notes

The authors have no financial conflicts of interest.

References

1. Expert Panel on Detection, Evaluation, and Treatment of High Blood Cholesterol in Adults. Executive summary of the third report of the National Cholesterol Education Program (NCEP) expert panel on Detection, Evaluation, and Treatment of high blood cholesterol in adults (Adult Treatment Panel III). JAMA. 2001; 285:2486–2497.

2. European Association for Cardiovascular Prevention & Rehabilitation. Reiner Z, Catapano AL, et al. ESC/EAS Guidelines for the management of dyslipidaemias: the Task Force for the management of dyslipidaemias of the European Society of Cardiology (ESC) and the European Atherosclerosis Society (EAS). Eur Heart J. 2011; 32:1769–1818.

3. Son JI, Chin SO, Woo JT. The Committee for Developing Treatment Guidelines for Dyslipidemia, Korean Society of Lipidology and Atherosclerosis (KSLA). Treatment guidelines for dyslipidemia: summary of the expanded second version. J Lipid Atheroscler. 2012; 1:45–59.

4. Bachorik PS, Ross JW. National Cholesterol Education Program recommendations for measurement of low-density lipoprotein cholesterol: executive summary. The National Cholesterol Education Program Working Group on Lipoprotein Measurement. Clin Chem. 1995; 41:1414–1420.

5. Anandaraja S, Narang R, Godeswar R, Laksmy R, Talwar KK. Low-density lipoprotein cholesterol estimation by a new formula in Indian population. Int J Cardiol. 2005; 102:117–120.

6. Anwar M, Khan DA, Khan FA. Comparison of Friedewald formula and modified Friedewald formula with direct homogeneous assay for low density lipoprotein cholesterol estimation. J Coll Physicians Surg Pak. 2014; 24:8–12.

7. Chen Y, Zhang X, Pan B, et al. Short paper A modified formula for calculating low-density lipoprotein cholesterol values. Lipids Health Dis. 2010; 9:52.

8. de Cordova CM, de Cordova MM. A new accurate, simple formula for LDL-cholesterol estimation based on directly measured blood lipids from a large cohort. Ann Clin Biochem. 2013; 50(Pt 1):13–19.

9. Friedewald WT, Levy RI, Fredrickson DS. Estimation of the concentration of low-density lipoprotein cholesterol in plasma, without use of the preparative ultracentrifuge. Clin Chem. 1972; 18:499–502.

10. Hattori Y, Suzuki M, Tsushima M, et al. Development of approximate formula for LDL-chol, LDL-apo B and LDL-chol/LDL-apo B as indices of hyperapobetalipoproteinemia and small dense LDL. Atherosclerosis. 1998; 138:289–299.

11. Vujovic A, Kotur-Stevuljevic J, Spasic S, et al. Evaluation of different formulas for LDL-C calculation. Lipids Health Dis. 2010; 9:27.

12. Scharnagl H, Nauck M, Wieland H, März W. The Friedewald formula underestimates LDL cholesterol at low concentrations. Clin Chem Lab Med. 2001; 39:426–431.

13. Martin SS, Blaha MJ, Elshazly MB, et al. Comparison of a novel method vs the Friedewald equation for estimating low-density lipoprotein cholesterol levels from the standard lipid profile. JAMA. 2013; 310:2061–2068.

14. Martins J, Olorunju SA, Murray LM, Pillay TS. Comparison of equations for the calculation of LDL-cholesterol in hospitalized patients. Clin Chim Acta. 2015; 444:137–142.

15. Rubiés-Prat J, Reverter JL, Sentí M, et al. Calculated low-density lipoprotein cholesterol should not be used for management of lipoprotein abnormalities in patients with diabetes mellitus. Diabetes Care. 1993; 16:1081–1086.

16. Choi SY, Park HE, Kim MK, Shin CS, Cho SH, Oh BH. Difference between calculated and direct-measured low-density lipoprotein cholesterol in subjects with diabetes mellitus or taking lipid-lowering medications. J Clin Lipidol. 2012; 6:114–120.

17. Oliveira MJ, van Deventer HE, Bachmann LM, et al. Evaluation of four different equations for calculating LDL-C with eight different direct HDL-C assays. Clin Chim Acta. 2013; 423:135–140.

18. Kapoor R, Chakraborty M, Singh N. A leap above Friedewald formula for calculation of low-density lipoprotein-cholesterol. J Lab Physicians. 2015; 7:11–16.

19. Goodman DS, Hulley SB, Clark LT, et al. Report of the National Cholesterol Education Program Expert Panel on detection, evaluation, and treatment of high blood cholesterol in adults. Arch Intern Med. 1988; 148:36–69.

20. Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986; 1:307–310.

21. Hanneman SK. Design, analysis and interpretation of method-comparison studies. AACN Adv Crit Care. 2008; 19:223–234.

22. Passing H, Bablok W. A new biometrical procedure for testing the equality of measurements from two different analytical methods. Application of linear regression procedures for method comparison studies in clinical chemistry, Part I. J Clin Chem Clin Biochem. 1983; 21:709–720.

23. Bilic-Zulle L. Comparison of methods: Passing and Bablok regression. Biochem Med (Zagreb). 2011; 21:49–52.

24. Hwang YC, Ahn HY, Jeong IK, Ahn KJ, Chung HY. Optimal range of triglyceride values to estimate serum low density lipoprotein cholesterol concentration in Korean adults: the Korea National Health and Nutrition Examination Survey, 2009. J Korean Med Sci. 2012; 27:1530–1535.

25. Tanno K, Okamura T, Ohsawa M, et al. Comparison of low-density lipoprotein cholesterol concentrations measured by a direct homogeneous assay and by the Friedewald formula in a large community population. Clin Chim Acta. 2010; 411:1774–1780.

26. Onyenekwu CP, Hoffmann M, Smit F, Matsha TE, Erasmus RT. Comparison of LDL-cholesterol estimate using the Friedewald formula and the newly proposed de Cordova formula with a directly measured LDL-cholesterol in a healthy South African population. Ann Clin Biochem. 2014; 51(Pt 6):672–679.

27. Miller WG, Waymack PP, Anderson FP, Ethridge SF, Jayne EC. Performance of four homogeneous direct methods for LDL-cholesterol. Clin Chem. 2002; 48:489–498.

Supplementary Materials

The online-only Data Supplement is available with this article at http://dx.doi.org/10.4070/kcj.2016.46.5.688.

Supplementary Table 1

Comparison of estimated formulas to directly measurement LDL-C according to serum TG concentration (TG >400 mg/dL)

Supplementary Table 2

Lipid profiles of participants with serum TG concentrations >400 mg/dL (n=24)

Supplementary Table 3

Parameters of estimated formulas against directly-measured LDL-C

Supplementary Fig. 1

Q-Q plot of total study population. HDL: high-density lipoprotein, LDL-C: low-density lipoprotein.

Supplementary Fig. 2

Q-Q plot of community-based group. HDL: high-density lipoprotein, LDL-C: low-density lipoprotein.

Supplementary Fig. 3

Q-Q plot of hospital-based group. HDL: high-density lipoprotein, LDL-C: low-density lipoprotein.

Supplementary Fig. 4

Correlation of directly-measured LDL-C with estimated LDL-C. LDL-C: low-density lipoprotein cholesterol.

Supplementary Fig. 5

Intraclass correlation coefficients (98.75% confidence interval) for the degree of absolute agreement according to serum TG concentrations. LDL-C: low-density lipoprotein cholesterol.

TOOLS

Similar articles