Abstract
Computational fluid dynamics (CFD) is a mechanical engineering field for analyzing fluid flow, heat transfer, and associated phenomena, using computer-based simulation. CFD is a widely adopted methodology for solving complex problems in many modern engineering fields. The merit of CFD is developing new and improved devices and system designs, and optimization is conducted on existing equipment through computational simulations, resulting in enhanced efficiency and lower operating costs. However, in the biomedical field, CFD is still emerging. The main reason why CFD in the biomedical field has lagged behind is the tremendous complexity of human body fluid behavior. Recently, CFD biomedical research is more accessible, because high performance hardware and software are easily available with advances in computer science. All CFD processes contain three main components to provide useful information, such as pre-processing, solving mathematical equations, and post-processing. Initial accurate geometric modeling and boundary conditions are essential to achieve adequate results. Medical imaging, such as ultrasound imaging, computed tomography, and magnetic resonance imaging can be used for modeling, and Doppler ultrasound, pressure wire, and non-invasive pressure measurements are used for flow velocity and pressure as a boundary condition. Many simulations and clinical results have been used to study congenital heart disease, heart failure, ventricle function, aortic disease, and carotid and intra-cranial cerebrovascular diseases. With decreasing hardware costs and rapid computing times, researchers and medical scientists may increasingly use this reliable CFD tool to deliver accurate results. A realistic, multidisciplinary approach is essential to accomplish these tasks. Indefinite collaborations between mechanical engineers and clinical and medical scientists are essential. CFD may be an important methodology to understand the pathophysiology of the development and progression of disease and for establishing and creating treatment modalities in the cardiovascular field.
Computational fluid dynamics (CFD) is a mechanical engineering field for comprehensively analyzing fluid flow, heat transfer, and associated phenomena with the use of computer-based simulation. The technique is very powerful and spans a wide range of areas. In the beginning, CFD was primarily limited to high-technology engineering areas-, but now it is a widely adopted methodology for solving complex problems in many modern engineering fields. CFD is becoming a vital component in the design of industrial products and systems. Examples are aerodynamics and hydrodynamics of vehicles, power plants including turbines, electronic engineering, chemical engineering, external and internal environmental architectural design, marine and environmental engineering, hydrology, meteorology, and biomedical engineering.1)2) The merit of CFD is developing new and improved devices and system designs, and optimization is conducted on existing equipment through computational simulations resulting in enhanced efficiency and lower operating costs. However, CFD is still emerging in the biomedical field. The main reason why CFD in the biomedical field has lagged behind is the tremendous complexity of human anatomy and human body fluid behavior. Recently, biomedical research with CFD is more accessible because high performance hardware and software are easily available with advances in computer science.1)
The study of fluid mechanics includes the study of fluids either in motion (fluid in dynamic mode) or at rest (fluid in stationary mode). CFD is usually dedicated to fluids that are in motion, and how the fluid flow behavior influences processes. Additionally, the physical characteristics of fluid motion can usually be described through fundamental mathematical equations, usually in partial differential form, which govern the process of interest and are often called governing equations. These mathematical equations are solved by being converted by computer scientists using high-level computer programming languages. The computations reflect the study of fluid flow through numerical simulations, which involves employing programs performed on high-speed digital computers to attain numerical solutions.2)
Using CFD, medical researchers can gain an increased knowledge of how body fluids and system components are expected to perform, to make the required improvements for bio-fluid physiology studies, and to develop medical devices. CFD offers chances for simulation before a real commitment is undertaken to execute any medical design alteration and may provide the correct direction to develop medical interventions.
Computational fluid dynamics is usually performed with use of commercial CFD codes. CFD codes are structured by numerical algorithms that consider fluid-flow problems. All CFD codes must contain three main components to provide useful information; 1) a pre-processor, 2) a solver, and 3) a post-processor.1)
Pre-processing consists of inputting a fluid flow problem into a CFD program. This includes defining the geometry of the region of interest, grid or mesh generation, selection of the physical and chemical phenomena that need to be modeled, a definition of fluid properties, and specification of appropriate boundary conditions at the inlet and outlet. The larger the number of cell grids the better the solution accuracy. The accuracy of a solution and the required time for computational problem solving are dependent on grid fineness. Most of the time spent is devoted to this process. In cardiovascular systems, computational imaging tools may confer the grid generation information, but limitations are that the resolution of current imaging tools is still low and geometry varies according to the cardiac cycle. Blood acts as a non-Newtonian fluid, because blood has varying viscosities according to its shear rate. Fig. 1 shows the correlation between blood viscosity and shear rate.3-5) Thus, the correct viscosity model using a mathematical equation should be selected according to the range of shear rates. The energy conservation law of fluid motion is an important consideration for basic concepts. Boundary conditions, such as blood pressure, blood flow velocity, and temperature are readily available from invasive and non-invasive measurements based on the region of interest. Another essential consideration is that these boundary conditions also vary according to the cardiac cycle and the unique conditions of coronary circulation. Fig. 2 shows a sample of these pressure and velocity profiles during cardiac cycles for modeling and CFD.6)
Numerical solution techniques are available such as finite difference, finite element, finite volume, and spectral methods. Each has a distinct numerical technique, but the basis of the solver is to perform an approximation of unknown flow variables by means of simple functions, discretisation by substitution of the approximations into the governing flow, and an algebraic solution. If the user uses a solution technique, the time spent depends upon the calculating capacity of the computer. Usually, the finite volume method is adopted for cardiovascular systems.
The object of this process is to visualize the computational results. Many visualization tools have been developed, including domain geometry and grid display, vector plots, line and shaded contour plots, two-dimensional and three-dimensional surface plots, particle tracking, and color postscript outputs. After this process, the researcher can easily understand the simulation results. For example, the changes in blood flow profiles, pressure distribution, wall shear stress (WSS), oscillating shear index (OSI), and shear rate can be visualized using color rendering techniques. Furthermore, a cyclic motion view can be obtained during cardiac cycles.
Recently, medical researchers have used simulation tools to assist in predicting the behavior of circulatory blood flow inside the human body. Computational simulations provide invaluable information that is extremely difficult to obtain experimentally and is one of the many CFD sample applications in the biomedical area in which blood flow through an abnormal artery can be predicted. CFD analysis is increasingly performed to study fluid phenomena inside the human vascular system. Medical simulations of circulatory function offer many benefits. They can lower the chances of postoperative complications, assist in developing better surgical procedures, and deliver a good understanding of biological processes, as well as more efficient and less destructive medical equipment such as blood pumps. Furthermore, medical applications using CFD have expanded not only into the diseased clinical situation, but also into health life supportives, such as sport medicine and rehabilitation. Several examples are discussed as follows.
Although many systemic risk factors predispose development of atherosclerosis, it preferentially affects certain regions of circulation, suggesting that lesion-prone areas may at least in part be due to biomechanically related factors. Furthermore, luminal hemodynamics, such as flow velocity, pressure changes, and WSS have been suggested as other risk factors for developing coronary atherosclerosis.7-9)
Information regarding the spatial distribution of intraluminal hemodynamics of the coronary vascular tree are available using CFD.10-14) Fig. 3 shows an example of performing CFD from pre-processing to post-processing. At first, a mesh or grid of region of interest is generated from the coronary extract images of computerized tomogram. The researchers might use any three dimensional medical images. The Digital Imaging and Communications in Medicine (DICOM) files should be converted into a file which can be used in a soft ware analyzing three dimensional vector information. All the digitalized data, such as velocity and pressure information according as cardiac cycle as a boundary condition were selected to put into an appropriate algebraic solution. And, the next step is mathematic solving process by the computer. At this process, mechanical engineers and medical scientists should discuss about all the clinical situations for selecting an appropriate viscosity models due to non-Newtonian fluid analysis, governing equations. Final step is visualization process for user. There are so many representative processing results, such as pressure profiles, velocity profiles, particle tracing, time-averaged wall shear stress (TAWSS), OSI, etc. This figure shows high TAWSS, OSI at bifurcation. TAWSS shows higher at bifurcation apex, but OSI shows higher at lateral side of side branch.
Fig. 4 shows an final example of flow velocity and WSS profiles in a artificial coronary artery model.9) Low WSS and low flow velocity are formed at the outer wall of a curved artery at the bifurcation with the inner wall. Spatial fluctuations in flow-velocity and recirculation occur at the curved outer wall of the left anterior descending coronary artery and are due to differences in flow-velocity and shear stress, particularly during the declaration phase of pulsatile flow. These results suggest that hemorheologic properties may be a part of the atherogenic process in the bifurcated and curved areas.
This kind of study might be applied to a modified coronary artery geometry model or varying viscosity models.13)14) Furthermore, the effect of percutaneous coronary intervention15)16) and coronary bypass grafts17)18) can be simulated and suggest the best method of intervention. CFD may be useful to understand the biomechanical pathophysiology of atherosclerosis and its complications.
Fontan circulation, first described by Fontan and Baudet,19) is characterized by the absence of a right ventricle and functions under unique hemodynamics. The key targets of geometric correction of Fontan procedure are the separation of systemic and pulmonary venous return and establishing the pathway of a passive, direct, and unobstructed connection between the systemic venous return and the pulmonary artery (PA) for treating single ventricle physiology, as one example of congenital heart disease.
While the Fontan procedure is a classic treatment procedure for a functional single ventricle in patients with congenital heart diseases, it has a potentially harmful effect for normal circulation. The absence of a right ventricle induces a pressure elevation in the venous system. The basic pathophysiological mechanisms originate from increased central venous pressure and the superior vena cava (SVC) and inferior vena cava (IVC).
Elevated central venous pressure is poorly tolerated over time, particularly in the IVC, and has deleterious effects on liver and splanchnic circulation. Protein-losing enteropathy and plastic bronchitis20) characterize the worst outcomes. At the liver level, elevated central venous pressure may induce complex liver dysfunction and stimulate angiogenesis factors21) favoring a venovenous anastomosis, pulmonary venous fistula, and, potentially, aortopulmonary collateral anastomoses. At the lung level, the upper PA branches are poorly or not perfused, and the lymphatic circulation is globally impaired.22) The single ventricle faces a significant increase in total systemic resistance because it needs to "push" against not only the usual systemic resistance but also lung resistance. As a consequence, the systemic ventricle becomes hypertrophied, with elevated end-diastolic pressure, which diminishes diastolic performance.23)24) Several studies have focused on solving these problems.25-29)
Computational fluid dynamics was performed after artificially modeling the Fontan circulation using medical information. Fig. 5 shows the velocity profiles at maximal flow among cardiac cycle time periods. Significantly increased flows were driven from the SVC, particularly during inspiration, indicating that unmixed blood flow to the PA and blood flow in the IVC may be more congested during inspiration than during expiration. During standing and inspiration, blood flow profiles aggravate the stagnation of systemic venous blood flow return and failure of the blood mixing function, suggesting that an artificial pumping device is essential for correcting Fontan circulation failure.
This is another example of using CFD as a diagnositic tool for evaluating heart function.
Work of the heart (WHO) is calculated using a pressure-volume curve. Some new indirect diagnostic tools are available to evaluate the WOH. The modified Windkessel model was used with blood viscosity models to develop a mathematical model for estimating WOH utilizing the pulse waves between two points of a vessel. The human arterial system is a network of vessels that converts intermittent flow of the heart into steady flow through the capillaries and venous system. The modified Windkessel model is a type of lumped parameter model that allows simulation of blood flow in the entire circulatory system as an electrical circuit (Fig. 6).
In this figure, Qin, Q1, and Q1 are defined as the flow rate exiting from the left ventricle during systole, the flow rate passing through the peripheral system, and the flow rate passing through the distal system, respectively. Similarly, p1 and p2 are the pressures measured at the proximal and distal locations, representatives of central and peripheral blood pressure, respectively. Moreover, C1 and C2 are proximal and distal compliances, where L corresponds to the inertia of blood (L=0.017 mmHgs2/mL). Flow rate in the left ventricle can be calculated with the mathematical fluid analysis shown in Fig. 7 by measuring blood pressure curves at two points in the peripheral arteries (brachial and radial arteries).30) The blood viscosity model is essential to solve the problem of an increased burden of work on the heart, so further study will be needed to verify which viscosity model results are similar compared to in vivo results. However, this type of study might suggest the possibility of developing non-invasive devices for measuring WHO.31)32)
Physiology and diseases of the aorta, carotid, and cerebral arteries are also studied with CFD. CFD is being increasingly employed to understand carotid stenosis and its biological properties according to geometric risks,33-36) or via virtual prototyping to recommend the best design for surgical reconstruction during a carotid endarterectomy,37) and conjunctional research magnetic resonance images.37-42) Furthermore, CFD is being used to better understand blood flow through an aneurysm in the abdominal artery, and the development and progression of aortic dissection.43-47) In intracranial cerebral artery disease, CFD is also used to identify the geometric and hemodynamic risks for rupture of a cerebral aneurysm and for stent design for a cerebral aneurysm.48-52)
There are many advantages when considering CFD. Theoretical development in the computational sciences focuses on the construction and solution of governing equations and the study of various approximations to these equations. CFD complements experimental and analytical approaches by providing an alternative cost-effective means of simulating real fluid flow, particularly in human body fluids. CFD has the capacity to simulate flow conditions that are not reproducible during experimental tests found in geophysical and biological fluid dynamics, such as scenarios that are too huge, too remote, or too small to be simulated experimentally. Furthermore, CFD provides rather detailed visual and comprehensive information when compared to analytical and experimental fluid dynamics.
Although CFD is advantageous, it cannot easily replace experimental testing as a method to gather information for design purposes. Despite its many advantages, the researcher must consider the inherent limitations of applying CFD. Numerical errors occur during computations; therefore, there will be differences between the computed results and reality. Visualizing numerical solutions using vectors, contours, or animated movies of unsteady flow are the most effective ways to interpret the huge amount of data generated from numerical calculations. Wonderfully bright color pictures may provide a sense of realism to the actual fluid mechanics inside a flow system, but they are worthless if they are not quantitatively correct. Thus, numerical results must always be thoroughly examined before they are believed; therefore, a CFD user needs to learn how to properly analyze and make critical judgments about the computed results.
Another important comment is collaboration between mechanical engineers and medical scientists. Not any one department can deliver a result. Each discipline should provide feedback on the results at each step.
Rapid advances of many industrial applications in computer science are outstanding, which requires changes in CFD. This changing situation is partly attributed to the rapid evolution of CFD techniques and models. Excellent creative models for simulating complex fluid mechanics problems in the human body and therapeutic models are now being progressively applied, particularly with the availability of commercial CFD computer programs. The increasing use of these programs in medicine might reveal how demanding the practical problems analyzed by CFD are. With decreasing hardware costs and rapid computing times, researchers and medical scientists may be relying increasingly on this reliable CFD tool to deliver accurate results. However, a realistic multidisciplinary approach is essential to accomplish these tasks. Indefinite collaborations between mechanical engineers and clinical and medical scientists are essential. CFD may be an important methodology for understanding the pathophysiology of developing and progressing cardiovascular disease and for establishing creative treatment modalities in the cardiovascular field.
Figures and Tables
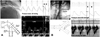 | Fig. 2Pressure and velocity of the coronary artery and aorta as a boundary condition in the bifurcation model (Lee et al.). A: left coronary artery. B: abdominal aorta. |
 | Fig. 3An example of CFD in left coronary artery. Finite volume method, adapting Rhie-Chow algorithm, computed with ANSYS CFX package program (Anflux, Seoul, Korea) in SUN SPARC station 20 (Sun Korea Co., Seoul, Korea) were used. At first, a mesh or grid of region of interest is generated from the coronary extract images of computerized tomogram. All the digitalized data velocity, pressure information according as cardiac cycle as a boundary condition was selected to put into an appropriate algebraic solution. And, the next step is mathematic solving process by the computer. At this process, mechanical engineers and medical scientists should discuss about all the clinical situations for selecting an appropriate algebraic solution. Final step is visualization process for user. There are so many representative processing results, such as pressure profiles, velocity profiles, particle tracing, time-averaged wall shear stress (TAWSS), oscillating shear index (OSI), etc. This figure shows high TAWSS, OSI at bifurcation. |
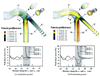 | Fig. 4The velocity vectors (upper) and distribution of wall shear stress (lower) in the coronary artery model. Prominent abrupt changes in velocity and wall shear stress at the outer wall around the branched site are noted during the deceleration period. |
 | Fig. 5Maximal velocity profile at inspiration (A) and expiration (B) in the supine position and inspiration (C) and expiration (D) in the standing position at an model of Fontan circulation. Tube structures represent cross-shaped reconstructed model of superior vena cava, inferior vena cava, right pulmonary artery, and left pulmonary artery at upper, lower, left and right tube. |
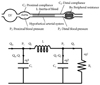 | Fig. 6Modified Windkessel model for the human arterial system (Qin, Q1, and Q1 are defined as the flow rate exiting from the left ventricle during systole, the flow rate passing through the peripheral system, and the flow rate passing through the distal system, respectively. Similarly, p1 and p2 are the pressures measured at the proximal and distal locations, respectively. C1 and C2 are proximal and distal compliances where L corresponds to the inertia of blood. |
References
1. Versteeg HK, Malalasekera W. Introduction To Computational Fluid Dynamics. The Finite Volume Method. 1995. 1st ed. New York: Longman Scientific & Technical.
2. Tu J, Yeoh GH, Liu C. Computational Fluid dynamics. A Practical Approach. 2008. 1st ed. Oxford: Elesevier.
3. Fung YC. Biomechanics. 1981. New York: Springer-Verlag.
4. Cho YI, Cho DJ. Hemorheology and microvascular disorders. Korean Circ J. 2011. 41:287–295.
5. Nichols WW, O'Rouke MF. McDonald's Blood Flow in Arteries Theoretical, Experimental and Clinical Principles. 2005. 5th ed. London: Hodder Arnold.
6. Lee BK, Kwon HM, Hong BK, et al. Hemodynamic effects on atherosclerosis-prone coronary artery: wall shear stress/rate distribution and impedance phase angle in coronary and aortic circulation. Yonsei Med J. 2001. 42:375–383.
7. Friedman MH, Deter OJ, Mar FF, Bargeron CB, Hutchins GM. Arterial geometry affects hemodynamics: a potential risk factor for atherosclerosis. Atherosclerosis. 1983. 46:225–231.
8. Fuster V, Badimon L, Badimon J, Chesebro JH. The pathogenesis of coronary artery disease and acute coronary syndromes. N Engl J Med. 1992. 326:242–250.
9. Lee BK, Kwon HM, Kim DS, et al. Computed numerical analysis of the biomechanical effects on coronary atherogenesis using human hemodynamic and dimensional variables. Yonsei Med J. 1998. 39:166–174.
10. Qiu Y, Tarbell JM. Numerical simulation of pulsatile flow in a compliant curved tube model of a coronary artery. J Biomech Eng. 2000. 122:77–85.
11. Ramaswamy SD, Vigmostad SC, Wahle A, et al. Fluid dynamic analysis in a human left anterior descending coronary artery with arterial motion. Ann Biomed Eng. 2004. 32:1628–1641.
12. Giannoglou GD, Soulis JV, Farmakis TM, Giannakoulas GA, Parcharidis GE, Louridas GE. Wall pressure gradient in normal left coronary artery tree. Med Eng Phys. 2005. 27:455–464.
13. LaDisa JF Jr, Olson LE, Douglas HA, Warltier DO, Kersten JR, Pagel PS. Alterations in regional vascular geometry produced by theoretical stent implantation influence distributions of wall shear stress: analysis of a curved coronary artery using 3D computational fluid dynamics modeling. Biomed Eng Online. 2006. 16:40.
14. Papafaklis MI, Bourantas CV, Theodorakis PE, Katsouras CS, Fotiadis DI, Michalis LK. Association of endothelial shear stress with plaque thickness in a real three-dimensional left main coronary artery bifurcation model. Int J Cardiol. 2007. 115:276–278.
15. Lee BK, Lee JY, Hong BK, et al. Hemodynamic analysis of coronary circulation in angulated coronary stenosis following stenting. Yonsei Med J. 2002. 43:590–600.
16. Ramaswamy SD, Vigmostad SC, Wahle A, et al. Comparison of left anterior descending coronary artery hemodynamics before and after angioplasty. J Biomech Eng. 2006. 128:40–48.
17. Sankaranarayanan M, Chua LP, Ghista DN, Tan YS. Computational model of blood flow in the aorto-coronary bypass graft. Biomed Eng Online. 2005. 4:14.
18. Freshwater IJ, Morsi YS, Lai T. The effect of angle on wall shear stresses in a LIMA to LAD anastomosis: numerical modelling of pulsatile flow. Proc Inst Mech Eng H. 2006. 220:743–757.
19. Fontan F, Baudet E. Surgical repair of tricuspid atresia. Thorax. 1971. 26:240–248.
20. Feldt RH, Driscoll DJ, Offord KP, et al. Protein-losing enteropathy after the Fontan operation. J Thorac Cardiovasc Surg. 1996. 112:672–680.
21. Starnes SL, Duncan BW, Kneebone JM, et al. Angiogenic proteins in the lungs of children after cavopulmonary anastomosis. J Thorac Cardiovasc Surg. 2001. 122:518–523.
22. Matthews IL, Fredriksen PM, Bjørnstad PG, Thaulow E, Gronn M. Reduced pulmonary function in children with the Fontan circulation affects their exercise capacity. Cardiol Young. 2006. 16:261–267.
23. Gewillig M. The Fontan circulation. Heart. 2005. 91:839–846.
24. Cheung YF, Penny DJ, Redington AN. Serial assessment of left ventricular diastolic function after Fontan procedure. Heart. 2000. 83:420–424.
25. Gerdes A, Kunze J, Pfister G, et al. Addition of a small curvature reduces power losses across total cavopulmonary connections. Ann Thorac Surg. 1999. 67:1760–1764.
26. Myers CD, Boyd JH, Presson RG Jr, et al. Neonatal cavopulmonary assist: pulsatile versus steady-flow pulmonary perfusion. Ann Thorac Surg. 2006. 81:257–263.
27. Hager A, Fratz S, Schwaiger M, Lange R, Hess J, Stern H. Pulmonary blood flow patterns in patients with Fontan circulation. Ann Thorac Surg. 2008. 85:186–191.
28. Bove EL, de Leval MR, Magliavacca F, Guadagni G, Dubini G. Computational fluid dynamics in the evaluation of hemodynamic performance of cavopulmonary connections after the Norwood procedure for hypoplastic left heart syndrome. J Thorac Cardiovasc Surg. 2003. 126:1040–1047.
29. de Zelicourt DA, Pekkan K, Parks J, Kanter K, Fogel M, Yoganathan AP. Flow study of an extracardiac connection with persistent left superior vena cava. J Thorac Cardiovasc Surg. 2006. 131:785–791.
30. Suh SH, Kaptan Y, Roh HW, et al. Estimation of Heart work by means of modified Windkessel model and different whole blood viscosity models. Proceedings of 7th International Conference on Computational Heat and Mass Transfer. 2011. Istanbul.
31. Westerhof N, Lankhaar JW, Westerhof BE. The arterial Windkessel. Med Biol Eng Comput. 2009. 47:131–141.
32. Yılmaz Y, Gündoğdu MY. A critical review on blood flow in large arteries: relevance to blood rheology, viscosity models and physiologic conditions. Korea-Aust Rheol J. 2008. 20:197–211.
33. Milner JS, Moore JA, Rutt BK, Steinman DA. Hemodynamics of human carotid artery bifurcations: computational studies with models reconstructed from magnetic resonance imaging of normal subjects. J Vasc Surg. 1998. 28:143–156.
34. Lee SW, Antiga L, Spence JD, Steinman DA. Geometry of the carotid bifurcation predicts its exposure to disturbed flow. Stroke. 2008. 39:2341–2347.
35. Lee SE, Lee SW, Fischer PF, Bassiouny HS, Loth F. Direct numerical simulation of transitional flow in a stenosed carotid bifurcation. J Biomech. 2008. 41:2551–2561.
36. Martin D, Zaman A, Hacker J, Mendelow D, Birchall D. Analysis of haemodynamic factors involved in carotid atherosclerosis using computational fluid dynamics. Br J Radiol. 2009. 82:S33–S38.
37. Hayase H, Tokunaga K, Nakayama T, et al. Computational fluid dynamics of carotid arteries after carotid endarterectomy or carotid artery stenting based on postoperative patient-specific computed tomography angiography and ultrasound flow data. Neurosurgery. 2011. 68:1096–1101. discussion 1101.
38. Xue YJ, Gao PY, Duan Q, et al. Preliminary study of hemodynamic distribution in patient-specific stenotic carotid bifurcation by image-based computational fluid dynamics. Acta Radiol. 2008. 49:558–565.
39. Hammer S, Jeays A, Allan PL, et al. Acquisition of 3-D arterial geometries and integration with computational fluid dynamics. Ultrasound Med Biol. 2009. 35:2069–2083.
40. LaDisa JF Jr, Bowers M, Harmann L, et al. Time-efficient patient-specific quantification of regional carotid artery fluid dynamics and spatial correlation with plaque burden. Med Phys. 2010. 37:784–792.
41. Marshall I. Computational simulations and experimental studies of 3D phase-contrast imaging of fluid flow in carotid bifurcation geometries. J Magn Reson Imaging. 2010. 31:928–934.
42. Groen HC, Simons L, van den Bouwhuijsen QJ, et al. MRI-based quantification of outflow boundary conditions for computational fluid dynamics of stenosed human carotid arteries. J Biomech. 2010. 43:2332–2338.
43. Frauenfelder T, Lotfey M, Boehm T, Wildermuth S. Computational fluid dynamics: hemodynamic changes in abdominal aortic aneurysm after stent-graft implantation. Cardiovasc Intervent Radiol. 2006. 29:613–623. Erratum in: Cardiovasc Intervent Radiol 2006;29:724.
44. O'Rourke MJ, McCullough JP. A comparison of the measured and predicted flowfield in a patient-specific model of an abdominal aortic aneurysm. Proc Inst Mech Eng H. 2008. 222:737–750.
45. Suh GY, Les AS, Tenforde AS, et al. Quantification of particle residence time in abdominal aortic aneurysms using magnetic resonance imaging and computational fluid dynamics. Ann Biomed Eng. 2011. 39:864–883.
46. Filipovic N, Ivanovic M, Krstajic D, Kojic M. Hemodynamic flow modeling through an abdominal aorta aneurysm using data mining tools. IEEE Trans Inf Technol Biomed. 2011. 15:189–194.
47. Karmonik C, Bismuth J, Davies MG, Shah DJ, Younes HK, Lumsden AB. A computational fluid dynamics study pre- and post-stent graft placement in an acute type B aortic dissection. Vasc Endovascular Surg. 2011. 45:157–164.
48. Tremmel M, Xiang J, Natarajan SK, et al. Alteration of intra-aneurysmal hemodynamics for flow diversion using enterprise and vision stents. World Neurosurg. 2010. 74:306–315.
49. Radaelli AG, Augsburger L, Cebral JR, et al. Reproducibility of haemodynamical simulations in a subject-specific stented aneurysm model: a report on the Virtual Intracranial Stenting Challenge 2007. J Biomech. 2008. 41:2069–2081.
50. Cebral JR, Mut F, Weir J, Putman C. Quantitative characterization of the hemodynamic environment in ruptured and unruptured brain aneurysms. AJNR Am J Neuroradiol. 2011. 32:145–151.
51. Sforza DM, Löhner R, Putman C, Cebral J. Hemodynamic Analysis of intracranial aneurysms with moving parent arteries: basilar tip aneurysms. Int J Numer Method Biomed Eng. 2010. 26:1219–1227.
52. Cebral JR, Mut F, Weir J, Putman CM. Association of hemodynamic characteristics and cerebral aneurysm rupture. AJNR Am J Neuroradiol. 2011. 32:264–270.




 PDF
PDF ePub
ePub Citation
Citation Print
Print




 XML Download
XML Download