Abstract
Purpose
To efficiently evaluate phased array coil performance using a software tool box with which we can make visual comparison of the sensitivity of every coil element between the real experiment and EM simulation.
Materials and Methods
We have developed a C++- and MATLAB-based software tool called Phased Array Coil Evaluator (PACE). PACE has the following functions: Building 3D models of the coil elements, importing the FDTD simulation results, and visualizing the coil sensitivity of each coil element on the ordinary Cartesian coordinate and the relative coil position coordinate. To build a 3D model of the phased array coil, we used an electromagnetic 3D tracker in a stylus form. After making the 3D model, we imported the 3D model into the FDTD electromagnetic field simulation tool.
Results
An accurate comparison between the coil sensitivity simulation and real experiment on the tool box platform has been made through fine matching of the simulation and real experiment with aids of the 3D tracker. In the simulation and experiment, we used a 36-channel helmet-style phased array coil. At the 3D MRI data acquisition using the spoiled gradient echo sequence, we used the uniform cylindrical phantom that had the same geometry as the one in the FDTD simulation. In the tool box, we can conveniently choose the coil element of interest and we can compare the coil sensitivities element-by-element of the phased array coil.
In magnetic resonance imaging (MRI), we can improve the signal-to-noise-ratio (SNR) of the images and reduce the scan time in parallel imaging by increasing the number of receiver coil elements (1). As the number of coil elements increases in the phased array coil, the complexity of the whole receive array coil increases and electromagnetic (EM) coupling among the coil elements also increases (2, 3). In developing phased array RF coils, comparing the imaging performances of each coil element with the ones predicted by an electromagnetic simulation is desirable (4). The imaging performance of each coil element usually differs from the one predicted by the EM simulation due to many RF engineering factors like EM couplings between the coil elements, the RF signal lines and the bias lines. The coil performance estimated from the finite difference time domain (FDTD) simulation could be used as a reference since we can exclude all the possible electromagnetic couplings between the coil elements by exciting only one element with opening the others.
Accurate coil modeling in the FDTD simulation should be assured in order to use the simulation results as references for the coil performance evaluation. The design, fabrication and evaluation of RF coils have been commonly performed for a given geometry of the coil elements (5, 6). However, it is often the case that the exact coil geometry is not available, for example, if we use a commercial RF coil or if we develop a RF coil through ad hoc modification of the coil shape (7). Kim et al. introduced a simple but efficient method to build 3D models of a RF coil in which modeling of the coil geometry was done manually in a 3D design tool with aids of the landmarks taken by a 3D tracker.
A phased array coil usually consists of multiple coil elements having irregular geometries in order to cover a specific area of the body. For example, in a helmet-style head coil like the one shown in Fig. 1, the shape of the coil elements placed at the upper part differ from the ones located in the inferior part of the coil. This is the case where the coil elements of the array have different shape and consequently the coil sensitivity profiles will vary considerably from coil to coil (8). Therefore, the performance of each coil element should be evaluated based on the image quality of every coil element (9).
In this paper, we introduce a tool box that can build a geometric model of the phase array coil automatically. The coil model, then, can be used to generate the coil sensitivity data through the EM simulation. The simulated coil sensitivity data will be compared with the real MRI experiment data on the tool box platform.
To build a 3D model of a phased array coil, we used the FASTSCAN (COBRA C1, Polhemus, USA) system which includes a 3D tracker in a stylus form that tracks the tip by receiving the electromagnetic signals emitted from the stylus. The stylus has a small tip the size of about 1 mm and the positioning accuracy of the 3D tracker is 0.75 mm within a 60 inch sphere. With the tracking tip we pinpointed few landmarks that define the coil element geometry (structure landmarks). Using these landmarks, a script is generated which contains all the information to produce the coil model. The script is loaded to a 3D design software which will generate the complete 3D model automatically. We imported the model into a FDTD EM simulator. The resulting simulation is imported together with a real MRI experiment, from the same examined phased array coil, to a visualization tool in order to analyze its performance. We have developed a C++ and MATLAB (MathWorks, Natick, MA, USA) based software tool called 'Phased Array Coil Evaluator' (PACE) with three main functions:
A complete scheme of the protocol to use PACE toolbox is shown in Fig. 2.
As explained in (7), the 3D model of the coil element could be built based on landmarks taken at the middle of the cooper lines which can constitute the skeleton of each coil elements in the whole model. In the present approach, a more accurate coil geometry structure will be generated by acquiring the landmarks at the sides of the cooper lines to construct the periphery of each coil element. As is represented in Fig. 3, the landmarks should be acquired consecutively at the periphery of the coil element. When the landmarks are connected consecutively from the first to the last point, the periphery of the coil element is obtained. This procedure should be repeated for all the coil channels.
The PACE tool box includes the Automatic Retrospective Coil Structure (ARCS) generator that requires the file given by the 3D tracker (.txt) containing the coordinates of each pinpointed landmark of the periphery. The ARCS tool will shape this periphery to create a surface with a user given thickness, creating a volumetric 3D model. In order to achieve an accurate representation of the coil geometry, ARCS builds each coil element as a series of connected triangular prisms and by repeating this procedure for every single channel, the whole 3D structure is created. ARCS automatically generates a script (.scr file) that can be used in a 3D design software to generate the complete 3D coil structure. In this work, the 3D design software AUTOCAD (Autodesk, San Rafael, California, USA) imports the ARCS's script and constructs the 3D coil model to further export the model in a compatible format with EM simulation software. Figure 4 shows how ARCS builds each coil geometry through triangular shape formation interconnecting the first three closest neighboring landmark points (Fig. 4a) with a giving thickness specified by the user. A second triangle is made up using one more neighboring point and the two closest points of the previous created triangle (Fig. 4b) and so on until connecting the all points of each coil element (Fig. 4c).
In order to make a good agreement between the coil sensitivity maps of the FDTD simulations and the acquired MRI data, we must keep the same parameters for both simulation and experiments, this condition is fundamental for the correct operation of the PACE tool box.
The MRI data must be a volumetric data set (3D data in a single file) of a uniform cylindrical water phantom placed at the magnet isocenter in the middle of the coil structure using the phase encoding gradient along the y- and z-directions with the field of view (FOV) being the same along the x- and y-directions (FOVx=FOVy) while the FOV along z-direction (FOVz) is leaved to the free choice of the user. The FDTD simulations must give the 3D B1 field map of each coil element, placing a uniform phantom model having the same dimensions and electrical properties of the experimental phantom and located inside the simulated coil structure considering the same FOV sizes of the MRI acquisitions. In this work, a 3T MRI system was used to acquire the volumetric data set and the above mentioned conditions were followed for the experiment and the simulations.
The coil sensitivity is defined as the B1 field induced by the RF coil at a given point per unit of supplied power (10, 11) and is possible to estimate the coil sensitivity map by calculating the magnetic field distribution. Since the phased array coil of this study is designed for receive-only mode, its receiving characteristics can be determined by simulating it in transmit mode according to the principle of reciprocity (10, 11, 12).
The 3D structure generated by AUTOCAD is exported to a FDTD software in order to compute the B1 field of the coil geometry. In this study, SEMCAD (SEMCAD X, SPEAG, Switzerland) (13) was used as FDTD tool. The simulation has been performed in a model having the same physical dimensions and electrical properties of the phantom used in the experimental work. Figure 5 shows the FDTD-computed B1 field distributions for a single-element coil after excitation.
Comparing the image quality of the coil elements based on orthogonal Cartesians planes (x=0, y=0, and z=0 planes) relative to the object under study will not be optimal if the coil element is not orthogonal with respect to the x-, y- or z-axis. In another words, if the coil element is well localized and has no coupling with other coil elements, the ordinary orthogonal Cartesian planes will not show the sensitivity of the coil as is illustrated at the bottom of Figure 6b. To overcome this limitation (8) intent to place the planes close to the coil element but still this will not be a consistent evaluation protocol since the geometry of the coil is not taken into account and the results may be biased. If the coil element is inclined, a more accurate measurement would be considering three relative orthogonal planes whose central axes x', y' and z' align perpendicularly to the plane of the coil element as is shown in Figure 6a. This rotated orthogonal coordinates make a consistent and unbiased visualization of the coils sensitivities because takes into account individual information of each coil element. Since the maximum imaging depth of a surface coil element is limited by its diameter we propose to evaluate the relocated relative planes at a distance proportional to the coil's radius r to visualize its maximum signal. The visualization of the coil sensitivities in rotated Cartesian coordinates relative to the coil element (x', y' and z') results more convenient if we want to compare the experimental coil sensitivities with the simulated ones, improving the evaluation of the SNR and the image-quality.
FASTSCAN tool was used again to obtain a second data set (.txt) containing three key points (Coil element plane points) from each coil element. This important points are used to generate the coil element plane which will be used later as a reference to form the relative planes used for the visualization of the coil sensitivity. Since the data of the FASTSCAN is given in units relative to its own reference, we need to co-register the measured points of each coil element with the respective spatial position of the image data obtained during the MRI experiment to create accurate coil element plane reference for each coil channel. The co-registration is a simple transformation of two or more set of data into one coordinate system. Following the protocol for MRI acquisition and simulations mentioned two sections before and having the acquired MRI data in millimeter units, a simple coordinate translation will be sufficient to achieve a good co-registration. At this point, the 3D MRI data is combined with the model obtained with the 3D scanner as shown in Figure 7. By computing the MRI data isocenter as well as the coil structure center, both the MRI data and the coil 3D model are matched to share the same spatial domain.
Each set of coil element plane points obtained by the FASTSCAN tool from each coil element after co-registration are used to create the normal vector of the coil's plane which is given by the cross-product:
where ni is the normal vector of the ith coil element plane and p0, p1 and p2 are the measured coil element plane points from each coil channel. In the following we exclusively refer to p0 as the point acquired at the center of the coil element while the other two are obtained at arbitrary points of its own periphery. We consider p0 = (a, b, c) where a, b and c represent the x, y and z coordinates of p0 respectively, using the same terminology for p1 and p2, we will have p1 = (d, e, f) and p2 = (g, h, i). The two arbitrary points (p1 and p2) will determine the orientation of the coil plane so these are given to the free choice depending on how the user wants to create the relative planes. In this work we choose p1 and p2 to be orthogonal with respect to p0 to obtain a standard visualization of the relative planes. After the normal vector is obtained, the coil element plane equation from each channel can be driven by using the plane equation:
where ni,x, ni,y and ni,z are the components of the normal vector ni given by Eq. 1.
Eq. 1 and 2 are used to find the plane equation for each coil element and form its reference coil element plane. Based on this plane reference, three more planes are generated for each coil channel, these planes are the relative planes: relative-axial (r-Axial), relative-sagittal (r-Sagittal), and relative-coronal (r-Coronal) planes. The so called relative planes are just planes in Cartesian coordinates rotated in the way that the rotated z-axis meets the center point perpendicularly of the coil element plane as shown in Figure 6. The r-Axial plane is parallel to the coil plane but shifted by a distance equal to the coil radius r, from the coil plane, then the plane equation will be similar to Eq. 2 but shifted by a distance r as given in Eq. 3.
The r-Sagittal and r-Coronal planes are determined by rotating the coil element plane of Eq.2 by 90° over a determined axis. For the r-Sagittal plane, p0 and p1 will determine the axis rotation vector as <u, v, w>=<d - a, e - b, f - c>while for the r-Coronal plane, p0 and p2 will form the axis rotation vector <u, v, w>=<g - a, h - b, i - c>. The matrix rotation about an arbitrary axis that passes through a point (p0), is presented in Eq. 4:
where L = u2 + v2 + w2, VW = v2 + w2, UW = u2 + w2, UV = u2 + v2, θ is the rotation angle, ζ= 1 - cosθ and δ = √L sin θ. In our case, the rotation angle θ is 90° which will simplify Eq. 4 and the whole procedure of relative planes creation is depicted in Figure 8.
Following the diagram of Figure 2 we develop the PACE toolbox in MATLAB and C++ for the phased array coil performance evaluation. A MATLAB version of the toolbox is shown in Figure 9. PACE (Fig. 9a) contains ARCS for the creation of the script to form the 3D structure, and a visualization environment (Fig. 9b and c) to observe the coil performance.
The physical helmet-style phased array coil structure of Figure 1 was scanned using the FASTSCAN 3D tracker. The data was imported to ARCS (PACE toolbox tool) by selecting the 'ARCS' option in the Figure 9a. The script generated by ARCS was loaded in AUTOCAD to create the 3D structure. The result of the modeling process took around 1 hour and is shown in Figure 10. Finally, the model was exported to SEMCAD for further EM simulations.
The simulated coil sensitivity maps were obtained from SEMCAD by exciting a single channel and opening the others to obtain the B1 field distributions, having a coupling-free reference to be compared with the real phased array coil. On the simulations, we set a uniform grid distribution in a FOV of 256×256×320 mm3 with the step sizes of hx = 2.0 mm, hy=2.0 mm and hz=1.25 mm. The total matrix size for the FDTD computation was 128×128×256. We also perform an MRI experiment using a spoiled GE 3D sequence, with: FOV = 256×256×320 mm, image matrix size = 256×256×32, TE = 7 ms, TR = 50 ms, FA = 50° and NEX=1. A cylindrical phantom with 200 mm of diameter and 300 mm height was used with εr = 76.7, µr = 1 and σ = 0.6 S/m, where εr, µr and σ are the relative permittivity, relative permeability and conductivity, respectively. For the FDTD simulations, the same phantom was modeled. Both simulations and experiments were conducted with similar characteristics as the above mentioned protocol demand.
By selecting 'Visualization' on the main window (Fig. 9a), the data from the MRI experiment, the simulation, and the coil element plane points were imported into PACE toolbox in order to compare and visualize the coil sensitivities and detect coupling by visual inspection. Two independent windows should be opened for comparing both set of data, one for the simulation (Fig. 9c) and other for the experimental (Fig. 9b) data.
In the visualization interface (Fig. 9b and c) is possible to select the channel of interest, select the ordinary orthogonal or the relative view, and also adjust the contrast for a better visualization (Fig. 9d). Additionally, in the left side of the PACE visualization window (Fig. 9b and c), the coil structure together with the isosurface of the phantom is displayed as a reference. Each coil element is represented by points and circles. The maximum signal of each coil element is highlighted with the same color as the selected coil revealing how its coil sensitivity is localized and its penetration through the phantom.
The performance of the real phased array coil was evaluated by visual comparison of the measured sensitivity maps with the simulated sensitivity maps from each coil element. Figure 11 shows a comparison between the real and the simulated sensitivity maps extracted from PACE. Figure 11a is the 3D view of the coil structure with highlighting in magenta the coil element #19 and its maximum signal localization on the simulated phantom isosurface while Figure 11b shows the same things for the experimental case, both from the same coil element. The simulated data is visualized in planes on Figure 11c-h while the MRI experimental results on Figure 11i-n. A visualization of the ordinary orthogonal Cartesian planes is shown for the simulation (Figs. 11c-e) and experiment (Figs. 11i-k) data while an observation through the relative planes is also shown for the simulation (Figs. 11f-h) and MRI (Figs. 11l-n) data.
An improvement of the retrospective 3D modeling of RF coils presented by Kim et al. was achieved by avoiding the time consuming procedure of building the 3D model by hand, reducing to hours a task that may take days. Figure 10 shows the final model of the real helmet-style phased array coil in Figure 1, where the dimensions and frame structure resemble each other. As can be seen, complex structures can be accurately modeled based on the physical coil design without been skillful in software modeling tools. With an accurate model of the real phased array coil is possible to perform also an accurate EM simulations. The performance of the real phased array coil is evaluated by visual comparison of the measured sensitivity maps with the simulated sensitivity maps, taking into account individual information from each coil element.
Both Cartesian and relative views complement each other to obtain a more complete coil performance analysis. Since the relative views are expected to show the maximum signal at every view for a particular well-decoupled coil element, these planes are more useful for coil sensitivity evaluations improving its analysis of SNR and quality-image. On the other hand, since the ordinary orthogonal Cartesian planes are related with the spatial localization of the coil elements, the visualization of these planes will be more useful for coupling evaluations. As is shown in Figure 11, the coupling of the real coil element was evident when we compared the localization and penetration of the sensitivity from the MRI and the simulation data. When a coil element is well decoupled, the ordinary orthogonal views will show signal intensity only on the plane's area where the coil element is localized (Fig. 11c-e). On the other hand, a coupled coil element will show a wide spread signal distribution along all views without any signal localization (Fig. 11i-k). The necessity of using relative planes is manifested in Figure 11c and d. Since ordinary Cartesian views will not show enough signal intensity at some views, the coil sensitivity and SNR evaluations may not be reliable. Based on the spatial position of the real coil channel #19 and its penetration area (Fig. 11b) as well as its coil sensitivity visualization on Figure 11i-k, is possible to see that this channel has more spread sensitivity than expected (Fig. 11a and Fig. 11c-e), which is not good for some parallel imaging techniques (14, 15), therefore, hardware improvements in this channel should be done. In future works, we plan to expand the function of the PACE tool box to include quantitative comparison between the simulated and experimental images, which needs further developments to take into account the transmit coil effects on the MRI image formation.
The present approach can be implemented to enhance existing coil performance methods that are based on SNR maps (9). With this tool, we could easily identify malfunctioning coil elements and also can be greatly used in improving phased array coils designs or performing periodic maintenance of coils in a more accurate and consistent manner.
Figures and Tables
 | Fig. 1A physical phased array 36 channel helmet-style coil structure.
(a) Lateral view and (b) frontal view of the 36-ch passed array coil structure.
|
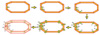 | Fig. 3Representation of the pinpointed landmarks (green circles) obtained by the 3D tracker of the FASTSCAN to define the coil element geometry. Starting at the upper-left figure: The first landmark acquired, second landmark, etc. Bottom-left: All the landmarks connected giving the periphery of the coil element. |
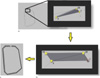 | Fig. 4Representation of the coil element construction done in ARCS by using the 3D tracker file containing the landmarks.
(a) Connection of the first three points of the first coil element at a specified thickness. (b) Second triangular prism created with the nearest neighboring point. Each coil element is completed by repeating this procedure until all the points are connected. (c) Creation of a complete coil element.
|
 | Fig. 5Distribution of the simulated magnetic field produced by a coil element of the phased array coil. The coil model was created by AUTOCAD with the ARCS (from PACE toolbox) script, while the FDTD evaluation was done in SEMCAD X.
(a) YZ plane, (b) XY plane, and (c) XZ plane. The signal was normalized to 0.000498 Vs/m^2.
|
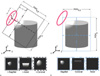 | Fig. 6Representation of the rotated Cartesian coordinate relative to the coil plane and the traditional one.
(a) The rotated Cartesian coordinate should meets the highest signal from a well decoupled element on a phase array coil. The rotated z-axis points perpendicularly to the center of the coil element plane. (b) Traditional Cartesian coordinate visualization planes at x=0, y=0 and z=0 will not fully represent the sensitivity of a well decoupled and localized coil element.
|
 | Fig. 7Representation of co-registration process of the coil structure points and the acquired volume sensitivity map.
(a) Isosurface of the Sum-of-Square (SoS) from the experimental data in mm. (b) Points representing each coil element in mm. (c) Both set of data located in different coordinate systems. (d) Both set of data after co-registration.
|
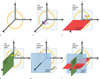 | Fig. 8Representation of the relative-planes creation.
(a) Three points (Coil element plane points) representing each coil element. (b) Computed coil element plane using Eq. 2. (c) The r-Coronal plane generated by rotating 90° the coil element plane with an axis rotation along x'. (d) The r-Sagittal plane generated by rotating 90° the coil element plane with an axis rotation along y'. Equation 4 was used in (c) and (d) cases. (e) The r-Axial plane generated using Eq. 3, the coil element plane shifted to a distance given by the radius of the coil element. (f) The three relative-planes and coil element plane positions.
|
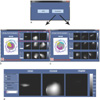 | Fig. 9The MATLAB-based PACE toolbox visualization software comparing the sensitivities of the coil elements between the real MRI experiment and the expected performance through the FDTD simulation.
(a) Main PACE window where is possible to choose ARCS or the visualization window. (b) MRI experiment on PACE visualization window. (c) FDTD Simulation on PACE visualization window. (d) Zoom from the dotted box on (b). (b) and (c) shows coils #8, #19 and #1 from top to the bottom.
|
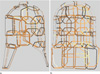 | Fig. 10SEMCAD visualization of the reconstructed 3D model of the 36 channel helmet-style coil structure shown in Fig. 1. (a) Lateral view and (b) frontal view of the 3D model. The 3D model was reconstructed by AUTOCAD using PACE tool box from the landmarks measured by the 3D tracker. |
 | Fig. 11Extracted figures from the MATLAB-based PACE toolbox visualization software, comparing the MRI data and the simulation sensitivities of a single coil element (channel #19) by the relative (Proposed) and Cartesian (Ordinary) views.
(a) Coil structure and simulation isosurface co-registered. In magenta, the analyzed coil element with its maximum signal distribution. (b) Coil structure and MRI data isosurface co-registered. In magenta, the analyzed coil element with its maximum signal. (c-e) Cartesian -axial, -coronal and -sagittal views, respectively, from the simulation. (f-h) relative -axial, -coronal and -sagittal views, respectively, from the simulation. (i-k) Cartesian -axial, -coronal and -sagittal views, respectively, from the MRI data. (l-n) relative -axial, -coronal and -sagittal views, respectively, from the MRI data.
|
Acknowledgements
This work was supported in part by Samsung Electronics and in part by a National Research Foundation of Korea (NRF) grant funded by the Korean Government (MEST), Ministry of Education and Science Technology (NRF-2013R1A2A2A03006812).
References
1. Roemer PB, Edelstein WA, Hayes CE, Souza SP, Mueller OM. The NMR phased array. Magn Reson Med. 1990; 16:192–225.
2. Lee RF, Giaquinto RO, Hardy CJ. Coupling and decoupling theory and its application to the MRI phased array. Magn Reson Med. 2002; 48:203–213.
3. Keil B, Wald LL. Massively parallel MRI detector arrays. J Magn Reson. 2013; 229:75–89.
4. Wong EY, Hillenbrand CM, Lewin JS, Duerk JL. Computer simulations for optimization of design parameters for intravascular imaging microcoil construction. Proc Intl Soc Mag Reson Med. 2003; 11:2386.
5. Constantinides C, Angeli S, Gkagkarellis S, Cofer G. Intercomparison of performance of RF coil geometries for high field mouse cardiac MRI. Concepts Magn Reson Part A Bridg Educ Res. 2011; 38A:236–252.
6. Hernandez D, Perez M, Lee SY. A bi-planar surface coil for parietal lobe imaging. Proc Intl Soc Mag Reson Med. 2013; 21:2793.
7. Kim DE, Park YM, Perez M, Hernandez D, Lee JH, Lee SY. Retrospective 3D modeling of RF coils using a 3D tracker for EM simulation. Concepts Magn Reson Part B. 2013; 43:126–132.
8. Wiggins GC, Triantafyllou C, Potthast A, Reykowski A, Nittka M, Wald LL. 32-channel 3 tesla receive-only phased-array head coil with soccer-ball element geometry. Magn Reson Med. 2006; 56:216–223.
9. Lattanzi R, Grant AK, Polimeni JR, et al. Performance evaluation of a 32-element head array with respect to the ultimate intrinsic SNR. NMR Biomed. 2010; 23:142–151.
10. Hoult DI. The principle of reciprocity in signal strength calculations-A mathematical guide. Concepts Magn Reson Part A. 2000; 12:173–187.
11. Hartwig V, Tassano S, Mattii A, et al. Computational analysis of a radiofrequency knee coil for low-field MRI using FDTD. Applied Magn Reson. 2013; 44:389–400.
12. Darrasse L, Kassab G. Quick measurement of NMR-coil sensitivity with a dual-loop probe. Review Scientific Instruments. 1993; 64:1841–1844.
13. SEMCAD X MRI. Web site. http://www.speag.com/.
14. Griswold MA, Jakob PM, Nittka M, Goldfarb JW, Haase A. Partially parallel imaging with localized sensitivities (PILS). Magn Reson Med. 2000; 44:602–609.
15. Seiberlich N, Griswold M. Parallel imaging in angiography. Magnetic Resonance Angiography. Springer;2012. p. 188.




 PDF
PDF ePub
ePub Citation
Citation Print
Print


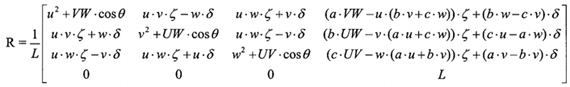
 XML Download
XML Download