PDF
ePub
Citation
Print
Introduction
Perfusion is a physiological parameter that refers to the delivery of oxygen and nutrients to tissues via the flow of blood (1). Cerebral blood flow (CBF) is generally quantified in terms of milliliters of blood per gram of tissue per second ml/g/sec (2). Perfusion measurements provide information regarding tissue viability and function, and are therefore of fundamental significance in the fields of medical research and clinical diagnostics.
Arterial spin labeling (ASL) perfusion (3), which involves an endogenous tracer on MR images, is one of the techniques used for perfusion imaging without injection or inhalation of contrast agent or radioisotopes (4). Generally speaking, a perfusion-weighted image gathered by this technique is derived from the subtraction of two successively acquired images: one with, and one without, the proximal labeling of arterial water spins after a short delay time (5). The water employed as a tracer in ASL is largely free-diffusible.
Most ASL approaches in common use employ either pulsed labeling (PASL) with an instantaneous spatially selective saturation or inversion pulse (6), or continuous labeling (CASL), most typically via flow-driven adiabatic fast passage (7). In both of these approaches, arterial spins are tagged outside the imaging slice. Tagged spins are then permitted to flow into the slice of interest, and the image is acquired. The control image is acquired without tagging, and the signal difference between the two scans provides perfusion-weighted imaging (PWI) to estimate a quantitative CBF (8). Several PASL methods, including EPI and signal targeting with alternating radiofrequency (RF) (EPISTAR) (9, 10), flow sensitive alternating inversion recovery (FAIR) (11, 12), and proximal inversion with a control for off-resonance effects (PICORE) (7), have been proposed. Recently, additional, better PASL methods have been proposed, such as the double inversion of both tagged and reference images (DIPLOMA) (13) and improved arterial spin labeling methods (IDOL) (14).
PASL signals generally depend on several parameters (15). First, the tagging efficiency of RF pulse (α) is a key factor in improving PASL signals. The second parameter is the tissue-to-blood partition coefficient (λ). Knowledge of λ is usually required for the quantification of CBF. λ changes during development of the brain and varies regionally in it, even among different gray matter structures, owing to variations in brain water content. In addition, λ would be expected to vary with the hematocrit, owing to changes in blood water content. The impact of using an incorrect value will result in errors in the quantifications of CBF. Third, the arterial transit delay time (δt) can affect measurements of the PASL signal. The transit delay for the flow of blood from the tagging region to the imaging slices in humans is not small compared with the T1 blood, and varies significantly across voxels, creating a variable attenuation of the ASL signal (7, 16); thus resulting in errors in the calculated CBF. Intravascular tagged blood that is flowing through the imaging slices and destined to perfuse more distal tissue can induce very large-amplitude focal artifacts in the difference signal that do not represent perfusion of the imaging slices (17). Finally, the longitudinal relaxation time of blood (T1b) and magnetic field strength (B0) are other factors.
The objective of this study was to determine optimal parameters using simulation for perfusion signals of PASL MRI. Perfusion signals, ΔM/M0b, derived from the Bloch equation were evaluated with the four most important parameters in PASL MRI: λ, T1b, δt, and B0. Although α is an important factor in acquisitions of high signals in ASL perfusion MRI, we did not include it in this simulation because perfusion signals are only linearly scaled by it.
Theory
PASL perfusion is based on the phenomenon of the inversion of signals. Fig. 1a is the schematic illustration of the labeling (inversion) of the spins in the arteries. The proton spins of blood flow to the arteries. The Bloch equation for tissue water, including flow, can be described as follows Eq. [1] :
in which M0 is the amplitude of the fully relaxed signal, f is the cerebral blood flow (ml g-1s-1), T1 is the longitudinal relaxation time of water in tissue (sec), and M(t), Ma(t), and Mv(t) are the magnetizations of water in tissue, arterial blood, and venous blood, respectively. Assuming that water is freely diffusible, Mv = M/λ and Ma = M0/λ, in which λ is the brain-blood partition coefficient (ml/g).
In PASL, the arterial blood is tagged near the imaging slice by inversion, and sequential images are acquired in which blood is alternately inverted and not inverted. We refer to these as tag and control states, respectively. Subtraction of the tag from the control images then leaves a difference signal, ΔM which is based on a general kinetic model for PASL signals (18):
in which M0b is the relaxed magnetization of arterial blood, α is the inversion efficiency, T1b is the T1 of arterial blood (sec), δt is the arterial transit delay (ATT, sec) from the application of the tag to the first arrival of tagged blood in the imaging slice, τ is the time width of the tag (sec), and T1 is the longitudinal relaxation time of water in tissue. TIt is the total labeling delay time. The timing diagram schematic of the PASL pulse sequence is provided in Fig. 1b.
The q-factor is a correction factor for the fact that the rate of decay of the tag switches from that of blood to the tag by flow. If we assume that blood water exchanges instantly and completely with tissue water upon reaching the capillary bed, and that tissue water follows single-compartment kinetics, then the q-factor is represented as Eq.[3]. A typical CBF value is 60 mL/100 mL/min, providing a rate constant of 0.01 s-1. The rate constant for the clearance of tagged water by T1 decay is 1/T1, or approximately 1.1 s-1. Thus, the clearance of the tag is dominated by T1 decay, and clearance by flow is likely to be insignificant. The q-factor is dimensionless and typically has a value near 1. If T1b = 1.6 sec, T1 for gray matter is 0.9 sec, f = 0.01 sec-1, λ = 0.9, δt = 1.0 sec, and TIt = 1.3 sec--which are the general parameters used at 3T (7) are assumed, the q-factor value is approximately 0.94. That is, it approaches 1 in accordance with the parameter values.
It is important to note that the expressions provided here for the difference signal assume that the parameters (δt, τ, T1b, etc.) are uniform across each voxel, which is certainly not the case. The actual signal is an average across heterogeneous populations of vessels and tissues, but we begin with these simple expressions to determine how well they describe the experimental data and provide insights into the relevant contrast mechanisms.
Materials and Methods
To determine how to change the q-factor and the corresponding magnetization signal for each of the parameter, we simulated (M/M0b and the q-factor based on Eq. [2] and [3]. Mathematica 7.0 (Wolfram Research Inc., IL, USA) software was used to simulate these parameters. Values of the parameters employed in the four simulations are shown in Table 1.
a. Tissue-to-blood partition coefficient λ effect on the q-factor and ΔM/M0b
To evaluate the effect of λ on the q-factor and (M/M0b, λ was varied according to brain tissue (19). For the well-perfused tissue, the incompleteness was no more than 1%. Therefore, the coefficient of tissue in brain would be only slightly affected by errors in the assumed perfusion (20). Parameter values to simulate λ were λgm = 1.03 ml/g , λwm = 0.86 ml/g, and λwh = 0.95 ml/g for gray matter, white matter, and whole brain, respectively. The range of TI was 0 ~ 5.0 sec. Other factors except for λ were fixed as α = 1, T1b = 1.6 sec, δt = 0.7 sec, and T1 = 0.977 sec. The simulation was assumed to be 3T.
b. Blood longitudinal relaxation time T1b effect on the q-factor and ΔM/M0b
To evaluate the effect of T1b on the q-factor and (M/M0b, the q-factor was evaluated for T1b values of 1.4, 1.6, and 2.2 sec for 1.5T (21, 22) 3.0T (22, 23), and 7T (22, 24) MRI. The range of TI was from 0 to 5 sec. (M/M0b was simulated using the simulation result of the q-factor. Factors except for T1b values were fixed as α = 1, δt = 0.7 sec, and λgm = 1.03 ml/g. The factor λ was used the value of gray matter in the brain. T1b values were 1.4 sec, 1.6 sec, and 2.2 sec, for 1.5T, 3.0T, and 7.0T respectively.
c. Arterial transit delay δt effect on the q-factor and ΔM/M0b
To evaluate the effect of δt on the q-factor and (M/M0b, the q-factor was evaluated for δt values of three different cases, which were 0.5, 0.7, and 0.9 sec. The range of TI was from 0 to 5 sec. (M/M0b was simulated using the simulation results for the q-factor. Factors except for the δt values were fixed as α = 1, T1b = 1.6 sec, and λgm = 1.03 ml/g. The factor λ was used the value of gray matter in the brain. The simulation was assumed to be 3T.
d. Strength of the magnetic field M0b effect on the q-factor and ΔM
The strengths of the magnetic field also do not affect the q-factor because there is no M0b term in Eq. [2]. Therefore, M0b simulated only the difference in magnetization. We considered the three different magnetic field strengths of 1.5T, 3.0T, and 7T in regard to our ASL perfusion MRI. In this simulation, we also took into consideration the longitudinal relaxation time of blood values (23). T1b values were 1 sec, 1.3 sec, and 1.5 sec, for 1.5T, 3.0T, and 7.0T respectively. Other factor values were α = 1, δt = 0.7 sec, λgm = 1.03 ml/g, and T1b values were assumed to be 1.4 sec, 1.6 sec, and 2.2 sec, for 1.5T, and 3.0T, and 7.0T, respectively.
Results
The maximum value of perfusion signals and the
corresponding inversion time are shown in Table 2.
a. Tissue-to-blood partition coefficient λ effect on the q-factor and ΔM/M0b
Fig. 2 shows the simulation results of the q-factor (2a) and ΔM/M0b (2b) in accordance with λ for gray matter, white matter, and whole brain. All three q-factor lines showed a similar pattern of monotonic decrease with increasing TI values. The q-factor was least, with the largest λ for all TI ranges.
ΔM/M0b shown in Fig. 2b was dramatically varied with varying λ. ΔM/M0b was increased with increasing λ or decreasing the q-factor. ΔM/M0b was progressively increased with increasing TI, reached a broad maximum at TI ~ 1.7 sec, and declined with further increases in TI for all three different tissues. The maximum values of ΔM/M0b were 0.390 at TI = 1.53 sec for gray matter, 0.365 at TI = 1.55 sec for whole brain, and 0.341 at TI = 1.58 sec for white matter.
b. Blood longitudinal relaxation time T1b effect on the q-factor and ΔM/M0b
Fig. 3 shows the simulation results of the q-factor (3a) and ΔM/M0b (3b) depended on the T1 of blood for three different magnetic strengths for the gray matter in the brain. All three q-factor lines evidenced a similar pattern of monotonic decrease with increasing TI values. The q-factor was largest with the largest T1b for all TI ranges.
ΔM/M0b shown in Fig. 3b increased progressively with increasing TI, reached a broad maximum at TI ~ 1.7 sec, and then declined with further increases in TI. Perfusion signals were increased with increasing T1b, as anticipated. The maximum values of ΔM/M0b were 0.351 at TI = 1.48 sec for T1b = 1.4 sec (1.5T), 0.390 at TI = 1.53 sec for T1b = 1.6 sec (3T), and 0.481 at TI = 1.64 sec for T1b = 2.2 sec (7T).
c. Arterial transit delay δt effect on the q-factor and ΔM/M0b
Fig. 4 shows the simulation results of the q-factor (3a) and ΔM/M0b (3b) depended on δt for gray matter in the brain at 3T. All three q-factor lines evidenced a similar pattern of monotonic decrease with increasing TI value. The q-factor was largest with the largest δt for all TI ranges.
ΔM/M0b shown in Fig. 4b increased progressively with increasing TI, reached a broad maximum at TI ~ 1.7 sec, and declined with further increasing TI. Perfusion signals were reduced with increasing δt. The maximum values of ΔM/M0b were 0.526 at TI = 2.1 sec for δt = 0.5 sec, 0.464 at TI = 2.3 sec for δt = 0.7 sec, 0.410 at TI = 2.5 sec for δt = 0.9 sec.
d. Strength of magnetic field M0b effect on ΔM
Fig. 5 shows the simulation results of ΔM depending on M0b for 1.5, 3.0, and 7.0T for the gray matter in the brain. ΔM increased progressively with increasing TI, reached a broad maximum at TI ~ 1.7 sec, and declined with further increasing TI values. Perfusion signals were increased with increasing B0, as anticipated. The maximum values of ΔM were 0.593 at TI = 1.48 sec for 1.5T, 1.154 at TI = 1.52 sec for 3 T, and 2.557 T at TI = 1.60 sec for 7 T.
Discussion
For improved CBF quantification using ASL MRI, several parameters must be optimized to reduce systematic errors. In this paper, we attempted to optimize four parameters: the tissue-to-blood coefficient (λ), the longitudinal relaxation time of blood (T1b), the arterial transit time (δt), and the of magnetic field strength (M0b) by simulating the q-factor and the perfusion signals of PASL MRI to determine the optimum labeling time (TI). Based on the simulation results, we can optimize the TI values with the highest perfusion signals (23, 25).
a. Tissue-to-blood partition coefficient λ effect on the q-factor and ΔM/M0b
The first simulation was the estimation of the q-factor and ΔM/M0b against TI depending on λ. Variations in λ occur in accordance with the water contents in brain tissues, including the white matter and gray matter. The q-factor was not dependent on the state of the brain tissues. However, the perfusion signals, ΔM/M0b, depended on brain tissues. Perfusion signals were at a maximum at TI = 1.53 sec for the gray matter. Perfusion signals in the gray matter were 1.14 times greater than that in white matter, due primarily to λ. The error for white matter may be greater than that for gray matter (26).
b. Blood longitudinal relaxation time T1b effect on q-factor and ΔM/M0b
The second simulation was the estimation of the q-factor and ΔM/M0b against TI depending on T1b. The q-factor did not depend greatly on T1b. However, perfusion signals, ΔM/M0b, were dependent on T1b. Perfusion signals were at a maximum at TI = 1.64 sec for T1b = 2.2 sec. The early part of the signal curve was weakly sensitive to T1b. T1b increases as hematocrit increases (27-29). Perfusion signals in the T1b = 2.2 sec (7T) were 1.37 times greater than in T1b = 1.4 sec (1.5T). Perfusion signals at 7T are increased by the increase in T1b. However, a loss in perfusion signals can occur as the result of a reduction in T2 and tagging efficiency loss.
c. Arterial transit delay δt effect on the q-factor and ΔM/M0b
The third simulation was the estimation of the q-factor and ΔM/M0b against TI depending on δt. The q-factor values were reduced with increasing TI for any δt. Because the signals rose rapidly after the delay, measurements at only one delay could potentially be strongly sensitive to variations in δt across the imaged plane. As a result, at any single time delay, the perfusion signal could evidence large errors. The quantification of CBF can be depended greatly upon the value of the transit delay.
d. Strength of magnetic field M0b effect on q-factor and ΔM
The last simulation was the estimation of ΔM against TI for three magnetic field strengths. The three q-factor curves had identical values because relaxed magnetization cannot affect the q-factor. The signal increase at higher field strengths was due primarily to the elongated T1. The maximum perfusion signal increased by approximately 51% at 3.0T compared to 1.5T. The perfusion signal at 7.0T would be approximately 431% greater than that seen at 1.5T. The signal is dependent on magnetic field strength and is greater at higher field strengths, due to the longer T1. In the case of ΔM for magnetic field strength as shown in the above result, it is possible to obtain high perfusion signals at high field strengths as the impact on TI. Additionally, however, because the amount of spin polarization increases with increases in M0b. Therefore, when multiplied by ΔM and M0b, the overall impact is significantly greater. Additionally, pseudo-continuous ASL (pCASL) and velocity-selective ASL (VSASL) are other types of PASL. We can also optimize those methods based on the simulation in this work.
Conclusion
In this paper, we reported the optimized TI values for several conditions to obtain the highest perfusion signal for PASL MRI. Both the q-factor and perfusion signals depended strongly on the longitudinal relaxation time of blood and the arterial transit delay. The tissue-to-blood coefficient affected the perfusion signals, but not the q-factor. Based on our results, it is important to select the optimized TI value by estimating the values of the longitudinal relaxation time of blood and the arterial transit delay.
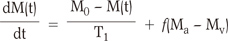
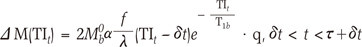
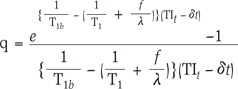
XML Download