Abstract
Purpose
Localization using MRI is difficult due to susceptibility induced artifacts caused by metal electrodes. Here we took an advantage of the B0 pattern induced by the metal electrodes by using an oblique-view imaging method.
Materials and Methods
Metal electrode models with various diameters and susceptibilities were simulated to understand the aspect of field distortion. We set localization criteria for a turbo spin-echo (TSE) sequence usingconventional (90° view) and 45° oblique-view imaging method through simulation of images with various resolutions and validated the criteria usingphantom images acquired by a 3.0T clinical MRI system. For a gradient-refocused echo (GRE) sequence, which is relatively more sensitive to field inhomogeneity, we used phase images to find the center of electrode.
Results
There was least field inhomogeneity along the 45° line that penetrated the center of the electrode. Therefore, our criteria for the TSE sequence with 45° oblique-view was coincided regardless of susceptibility. And with 45° oblique-view angle images, pixel shifts were bidirectional so we can detect the location of electrodes even in low resolution. For the GRE sequence, the 45° oblique-view anglemethod madethe lines where field polarity changes become coincident to the Cartesian grid so the localization of the center coordinates was more facilitated.
For neuro-electrophysiologic studies using metal electrodes, the knowledge of the precise location of these electrodes is important for both the experimental accuracy and efficiency. Magnetic resonance imaging (MRI) has been used for localizing recording sites or guiding neurosurgery such as deep brain stimulation (DBS) (1). But it has a critical problem called susceptibility artifact, caused by difference of susceptibility of electrodes that are usually made of metal. Metallic materials severely distort the main magnetic field (B0) and this inhomogeneity causes image artifacts. Aspects of susceptibility artifacts have been described well (2) and several groups experimentally and numerically examined the field perturbation and image artifact due to electrode (3-5), but it is still difficult to find accurate location of metal electrode.
There have been many studies to overcome this artifact of metal electrode so far. Previous studies have been focused on needle sheath, so they set electrode parallel to B0 field because it makes the sheath have minimal artifact (2-6). However, there is another artifact at a needle tip called blooming artifact (4). And for microelectrode, usually 20-30 µmin diameter at 100 µm from the tip end, electrode parallel to B0 cannot be distinguished well (7). Trajectory guidance systems (8, 9) or stereotactic atlas-based methods (10, 11) also have been introduced,but there is a possibility that the brain is moving during surgery.
Here, we used anoblique-viewangle method for the accurate localization of metal electrodes. Magnetic field patterns produced by the electrodes were simulated using numerical methods. The locations in the field patterns generated where the least inhomogeneity was produced were used for MR imaging. In particular, we show a case where perpendicular positioning of the metal electrodes with respect to the main field is used. We suggest that localization of electrode center can be done using a phase image for a gradient-refocused echo (GRE) sequence and also by using the signal pile-up pattern of a turbo spin-echo (TSE) sequence in 45° oblique-view angle, where the angle refers to readout line direction with respect to B0.
A first-order approximation of the B0 field perturbation induced by a magnetic susceptibility distribution can be represented as
where B0 is the main magnetic field strength, k is the Fourier domain coordinates, χ(r) is the magnetic susceptibility distribution and ΔB0 (r) is the perturbed field distribution (12, 13). The field perturbation induced by a metallic electrode was calculated by substituting the 3D spatial susceptibility distribution of an electrode to Eq. [1] (Fig. 1a). The 3D susceptibility distribution was modeled as a finite cylinder with uniform material.
Then we simulated signal pile-up patterns at various susceptibilities and resolutions in 90° and 45° oblique-view angles by applying virtual gradient and excitation RF to the calculated field map (Fig. 2a, b). The positional shift in the readout direction caused by field perturbation ΔB0 is Δx=ΔB0 (x,y,z)/GR (14). For simulation with various susceptibilities, we set electrodes with radius of 0.5 mm made of tungsten (χ = 77.2 ppm), titanium (χ= 182 ppm) and platinum (χ = 279 ppm) at 0.125 mm2 resolution (Fig. 3), and an electrode same as the one in phantom study (R = 0.25 mm, tungsten) was used for simulation with various resolutions. The lower resolution images (res = 0.15, 0.25, 0.5, 1.0 mm2) were made by down-sampling the base image with resolution of 0.05 mm2 and we simulated signal pile-up pattern with respect to the relative location of center of the electrode in a pixel (Fig. 4). All simulations were done under condition of RF bandwidth=1000 Hz and readout bandwidth = 130 Hz/pixel, using MATLAB (The Mathwork, Natick, MA, USA).
For phantom study, we localized a tungsten electrode with radius of 0.25 mm to the center of grid which has 0.5 mm width and fixed it with 1% agar gel. MR images were acquired on a 3.0T MRI scanner (Siemens, Tim Trio) using two dimensional TSE and GRE sequences with various resolutions (0.13, 0.25, 0.5, 1.0 mm2) in 90° and 45° view angle (Figs. 5, 6). And for the rat brain model, we used tungsten electrode with diameter of 0.125 mm inserted into an extracted rat brain fixed with paraformaldehyde. The 3DTSE sequence was used with 0.25×0.25×0.3 mm3 resolution (Fig. 7).
For TSE images, we set three points (a, b and c in Fig. 2a, b) that have local maximum intensity near the electrode from both simulated and experimentally acquired images by plotting the lines along the readout (RO) and the phase encoding (PE) direction. In general parallel or perpendicular view angle images, say 90°, where the pixel shifts occur unidirectionallyat a single readout line, we chose the center of the local maximums as the center of the electrode on the assumption that the amounts of pixel shift are similar in both direction, i.e., the severities of field distortion are similar in both positively and negatively distorted area. In other words, if we think of RO and PE axis as a coordinate system, we can estimate the coordinates of the center of the electrode as the PE coordinate of the point (c) and the RO coordinate of the middle of the two points (a, b) and another point (c) (Fig. 2c). On the other hand, in 45° or (90n+45)° oblique-view angle images, say 45°, pixel shifts are bidirectional and point (c) now lies on the PE line, meaning that it is given the center RO coordinate. And we found the point where the signal pile-up decreases rapidly, which makes it the center of PE coordinate, by plotting the max value of RO lines (Fig. 2d).
For GRE images, we chose the location of electrode as the center of the phase pattern in both 90° and 45° view angle.
With the metal electrode perpendicular to the main magnetic field (B0), field distortion due to susceptibility difference occurs as shown in Fig. 1a. As we can see in Fig. 1b, the 45° line across the center of the electrode experiences no or only minor inhomogeneity, which makes it the null-field line. In Fig. 2 we can see pixel shifts areunidirectional for 90° view angleand bidirectional for 45° oblique-view angle and the resulting location of electrode using our criteria for TSE images.
At 90°, our criterion for PE coordinate looks valid. But we can see that higher the susceptibility, worse the estimation of RO coordinates. It seems that the peaks of PE line-plot become more asymmetric with higher susceptibility. However, at 45° our criteria are effective regardless of susceptibilities.
The criterion for RO coordinate is valid at all resolutions. Furthermore,through simulation of signal pile-up pattern with respect to the relative location of center of the electrode in a pixel, we can estimate the location of center of the electrode with sub-pixel resolution by examining the signal level of pixels next to the center pixel. The PE coordinate is the point where the signal decreases most rapidly, rather than the point that the signal pile-up disappears. We have found that it has at least one pixel resolution's accuracy.
This method is quite accurate in finding the location
in both angles and all resolutions. However, 45° view angle is better due to its coincidence to the Cartesian
grid, and this advantage is further useful in high
resolution images.
Unlike our simulation results, PE coordinate at 90° view angle is by far incorrect. The criterion for RO coordinate seems to be accurate but we know that it is affected by susceptibility, so the resultsshould be regarded coincidental. The results at 45° are more accurate than at 90° at high resolution, and even though it seems to have similar accuracy to 90° results at low resolution, we should remember that we can estimate the location with sub-pixel resolution at 45°.
The result was acquired at the base pixel size nearly quadruple the cross sectional area of the electrode. At 90° view angle, we cannot decide which pixel in the yellow box the electrode is located exactly. But at 45°, we can precisely find the location of electrode with sub-pixel resolution that has accuracy down to just twice the cross sectional area of the electrode.
The criteria for localization of metal electrodes using 45° oblique-view angle method were defined by simulations and verified by experiments.
The GRE sequence is relatively more sensitive to field inhomogeneity (4) because it does not have refocusing processes. However in our case, this fact can be used to easily estimate the location of center of the electrode using the phase image. The results were quite accurate regardless of view angle, but 45° oblique-view angle has advantage that the lines where field polarity changes are coincident to the Cartesian grid, facilitating the localization of the center coordinate. We can expect reliable results even when the electrode is not exactly perpendicular to B0 if the slice thickness is thin enough.
On the other hand, the TSE sequence can overcome field inhomogeneity with its 180° refocusing pulse, thus obscuring the field distortion pattern in phase images. However, pixel shifts do occur if the field inhomogeneity is severe enough, even when using the TSE sequence. Even though the severe artifact due to metallic materials cannot be perfectly corrected (2), we can estimate the electrode center by analyzing the pattern of signal pile-up in these areas.
When the subject is exposed to field inhomogeneity, there will be signal void or pixel shift along readout line in the MR image. The pixels in positive field shift toward RO direction and those in negative field shift to the opposite direction. As we can see in Fig. 1a, each readout line meets only a single polarity of field inhomogeneity when we acquire an image in 90° view angle. Therefore the pixels shift to one direction on one readout line and then are piled up at specific point due to gradual change of the inhomogeneity. The reason why our criteria for 90° view angle were not valid is that the inhomogeneities of the area over the electrode and below the electrode in the image itselfare same but near center is not (see Fig. 1a). The larger susceptibility an electrode has, the greater inhomogeneity difference occurs. Therefore, although we can calculate the amount of pixel shift accurately, it is impossible to determine the location of electrode with unknown susceptibility in conventional view angle.
However, in 45° oblique-view angle, the readout line always meets both polarities of the field inhomogeneity and pixels either spread to opposite directions or accumulate to its center. The accumulated pixel will coincide with the RO coordinate of the electrode center since the magnitudes of field inhomogeneities arealmost equal. Additionally, since the readout direction is at 45° with the respect to B0, there exists a 'null-field line' (Figs. 1b, 2b) across the center of the electrode. Because there is low degree of pixel shift and signal pile-up here, the center position can be decided as the point where the maximum intensity drops sharply. Furthermore, pixels which are located close to the electrode experiences severe inhomogeneity and no RF excitation, which creates a series of signal void points until the signal pile-up point. Therefore, the decision criteria can also work well in low resolution images. Although there may be subtle difference in the sizes of positive and negative fields due to large susceptibility, simulation results showed that materials with susceptibility value around that of platinum could still be accurately localized.
Experiments for TSE sequence showed that the 45° case was almost identical to the simulation results, but 90° case was different that the PE coordinate deviated more and the RO coordinate was closer to the real position than expected. This is due to the fact that the field distortion pattern depends on a variety of factors concerning imaging parameters and material characteristics. Nevertheless, 45° oblique-view angle approach works excellently since it provides reliable pixel shift patterns regardless of field distortions.
Our work suggests an intuitive and reliable method for localizing the center of the electrode using conventional GRE and TSE sequences when the electrode is positioned perpendicular to the B0 field. However, further work is needed for cases where the angle between the electrode and B0 deviates from 90°.
We showed that the localization criteria were accurate when the metal electrodes are positioned perpendicular to the main field by using GRE phase image and TSE signal pile-up pattern. We took advantage of the 45° oblique-view angle to find accurate location in both GRE and TSE sequences. The criteria are robust to various susceptibilities and have credible accuracy at high resolution and are even capable of having sub-pixel accuracy at low resolution. Our study indicates that MRI, with its capability to image at arbitrary view angles, can be effectively used for accurate localization of metal electrodes used in invivo electrophysiology studies.
Figures and Tables
 | Fig. 1(a) Simulation results of field inhomogeneity pattern due to an electrode with d=125 µm, χ=77.2 ppm (tungsten). (b) Field inhomogeneity along the solid line (90°) and dashed line (45°) across the center of the electrode shown in (a). The blue line and red line in (b) indicate the 90° and 45 °line profiles, respectively. Note that there is a null-field line where least field inhomogeneity occurs in 45° line. |
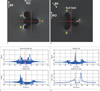 | Fig. 2Simulation results of signal pile-up patterns due to an electrode with d=250 µm, χ=77.2 ppm (tungsten) in (a) 90° and (b) 45° view angle and their RO/PE line-plots ((c) 90°, (d) 45°). The lines indicate the estimated coordinate center by using localization criteria. |
 | Fig. 3Simulation results of various susceptibilities with electrodes of R=0.5 mm, χ=77.2 ppm (a, d), 182 ppm (b, e), and 279 ppm (c, f) in 90° (a-c) and 45° (d-f). Red lines and green lines indicate the real center and incorrectly estimated coordinate center respectively. |
 | Fig. 4Simulation results of various resolutions with electrodes of R=0.25 mm and (a) res=0.15 mm2, (b) res=0.25 mm2, (c) res=0.5 mm2, (d) res=1.0 mm2. First rows are simulated TSE images and second rows show the relative location of electrodes in pixels of respective resolution. Third rows are the RO/PE line-plot results of images. Red lines indicate the coordinate center of the electrode. Each column shows how the relative location of an electrode affects the pixel pile-up pattern in image and localization of electrode in line-plots. |
 | Fig. 52DGRE results in (a) 90° and (b) 45°. First and second rows are GRE magnitude and phase images of an electrode, respectively. Third rows show the grid which marks the real location of electrodes. Resolution of each column is shown at the top of the first image. Red lines indicate the estimated center of the electrode. |
 | Fig. 62DTSE results in (a) 90° and (b) 45°. Each subfigure consists of four sets of images with respective resolution that are shown at the top left of the image sets. In each image set, there are TSE images of an electrode and the reference grid on the left side and respective RO/PE line-plots on the right side. Red lines indicate the estimated center of the electrode. |
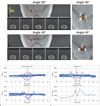 | Fig. 7(a) 3DTSE results for the rat brain model. The image on the top left of each view angle is the axial image showing the electrode position and image below it is series of 5 coronal images showing inhomogeneity due to the electrode. The regions near electrode center (red box) are magnified in the image on the right. (b) and (c) are RO/PE line-plots at the position of the yellow lines in (a) for 90° and 45°, respectively. Red lines indicate the estimated center and the yellow box shows the expected region where the electrode is located. Note that there is small amount of image distortion at the center slice of coronal image in 45° view angle. It implies that the RO line of that slice has almost crossed the electrode center, where the null-field exists. |
Acknowledgements
This work was supported by the Korea Science and Engineering Foundation (KOSEF) grant funded by the Korea government (MEST) (No. 2010-001538).
References
1. Schrader B, Hamel W, Weinert D, Mehdorn HM. Documentation of electrode localization. Mov Disord. 2002. 17:S167–S174.
2. Lüdeke KM, Röschmann P, Tischler R. Susceptibility artifacts in NMR imaging. Magn Reson Imaging. 1985. 3:329–343.
3. Ladd ME, Erhart P, Debatin JF, Romanowski BJ, Boesiger P, McKinnon GC. Biopsy needle susceptibility artifacts. Magn Reson Med. 1996. 36:646–651.
4. Müller-Bierl B, Graf H, Lauer U, Steidle G, Schick F. Numerical modeling of needle tip artifacts in MR gradient echo imaging. Med Phys. 2004. 31:579–587.
5. Martinez-Santiesteban FM, Swanson SD, Noll DC, Anderson DJ. Magnetic field perturbation of neural recording and stimulating microelectrodes. Phys Med Biol. 2007. 52:2073–2088.
6. Liu H, Hall WA, Martin AJ, Truwit CL. Biopsy needle tip artifact in MR-Guided Neurosurgery. J Magn Reson Imaging. 2001. 13:16–22.
7. Matsui T, Koyano KW, Koyama M, et al. MRI-based localization of electrophysiological recording sites within the cerebral cortex at single-voxel accuracy. Nat Methods. 2007. 4:161–168.
8. Truwit CL, Liu H. Prospective stereotaxy: a novel method of trajectory alignment using real-time image guidance. J Magn Reson Imaging. 2001. 13:452–457.
9. Martin AJ, Larson PS, Ostrem JL. Placement of deep brain stimulator electrodes using real-time high-field interventional magnetic resonance imaging. Magn Reson Med. 2005. 54:1107–1114.
10. Zrinzo L, Zrinzo LV, Tisch S, et al. Stereotactic localization of the human pedunculopontine nucleus: atlas-based coordinates and validation of a magnetic resonance imaging protocol for direct localization. Brain. 2008. 131:1588–1598.
11. Oya H, Kawasaki H, Dahdaleh NS, Wemmie JH, Howard MA. Stereotactic atlas-based depth electrode localization in the human amygdala. Stereotact Funct Neurosurg. 2009. 87:219–228.
12. Salomir R, De Senneville BD, Moonen CTW. A fast calculation method for magnetic field inhomogeneity due to an arbitrary distribution of bulk susceptibility. Concept Magn Reson B. 2003. 19B:26–34.
13. Koch KM, Papademetris X, Rothman DL, de Graaf RA. Rapid calculations of susceptibility-induced magnetostatic field perturbations for in vivo magnetic resonance. Phys Med Biol. 2006. 51:6381–6402.
14. Hopper TAJ, Vasilic B, Pope JM, et al. Experimental and computational analyses of the effects of slice distortion from a metallic sphere in an MRI phantom. Magn Reson Imaging. 2006. 24:1077–1085.




 PDF
PDF ePub
ePub Citation
Citation Print
Print


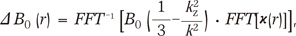
 XML Download
XML Download