1. Lüdeke KM, Röschmann P, Tischler R. Susceptibility artefacts in NMR imaging. Magn Reson Imaging. 1985. 3:329–343.
2. Schenck JF. The role of magnetic susceptibility in magnetic resonance imaging: MRI magnetic compatibility of the first and second kinds. Med Phys. 1996. 23:815–850.
3. Butts K, Pauly JM, Daniel BL, Kee S, Norbash AM. Management of biopsy needle artifacts: techniques for RF-refocused MRI. J Magn Reson Imaging. 1999. 9:586–595.
4. Cho ZH, Kim DJ, Kim YK. Total inhomogeneity correction including chemical shifts and susceptibility by view angle tilting. Med Phys. 1988. 15:7–11.
5. Lu W, Pauly KB, Gold GE, Pauly JM, Hargreaves BA. SEMAC: Slice Encoding for Metal Artifact Correction in MRI. Magn Reson Med. 2009. 62:66–76.
6. Arbogast-Ravier S, Gangi A, Choquet P, Brunot B, Constantinesco A. An in Vitro Study at Low Field for MR Guidance of a Biopsy Needle. Magn Reson Imaging. 1995. 13:321–324.
7. Ladd ME, Erhart P, Debatin JF, Romanowski BJ, Boesiger P, McKinnon GC. Biopsy needle susceptibility artifacts. Magn Reson Med. 1996. 36:646–651.
8. Lufkin R, Teresi L, Hanafee W. New Needle for MR-Guided Aspiration Cytology of the Head and Neck. AJR Am J Roentgenol. 1987. 149:380–382.
9. Lufkin R, Teresi L, Chiu L, Hanafee W. A Technique for MR-Guided Needle Placement. AJR Am J Roentgenol. 1988. 151:193–196.
10. Liu H, Martin AJ, Truwit CL. Interventional MRI at High-Field (1.5 T): Needle Artifacts. J Magn Reson Imaging. 1998. 8:214–219.
11. Balac S, Caloz G, Cathelineau G, Chauvel B, de Certaines JD. Integral method for Numerical Simulation of MRI Artifact Induced by Metallic Implants. Magn Reson Med. 2001. 45:724–727.
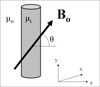
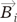 and
and 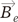 denote the magnetic field inside and outside cylinder, respectively.
denote the magnetic field inside and outside cylinder, respectively.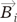 and
and 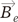 denote the magnetic field inside and outside cylinder, respectively.
denote the magnetic field inside and outside cylinder, respectively.