1. Urban B, Ratner L, Fishman E. Three-dimensional Volume-rendered CT Angiography of the Renal Arteries and Veins: Normal Anatomy, Variants, and Clinical Application 1. Radiographics. 2001. 21(2):373–386.
2. Zanzonico P, Rothenberg L, Strauss H. Radiation Exposure of Computed Tomography and Direct Intracoronary Angiography Risk has its Reward. J Am Coll Cardiol. 2006. 47(9):1846–1849.
3. Lee VS. Cardiovascular MRI: Physical principles to practical protocols. 2006. Philadelpia: Lippincott Williams & Wilkins.
4. Pruessmann KP, Weigher M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magn Reson Med. 1999. 42(5):952–962.
5. Sodickson DK, Manning WJ. Simultaneous acquisition of spatial harmonics (SMASH): fast imaging with radiofrequency coil arrays. Magn Reson Med. 1997. 38(4):591–603.
6. Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med. 2002. 47(6):1202–1210.
7. Sodickson D, McKenzie C, Li W, Wolff S, Manning W, Edelman R. "Contrast-enhanced 3D MR Angiography with Simultaneous Acquisition of Spatial Harmonics: A Pilot Study 1. Radiology. 2000. 217(1):284–289.
8. Wilson GJ, Hoogeveen R, Willinek W, Muthupillai R, Maki J. "Parallel Imaging in MR Angiography". Top Magn Reson Imaging. 2004. 15(3):169–185.
9. Lustig M, Donoho D, Pauly J. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007. 58(6):1182–1195.
10. Donoho DL. Compressed sensing. IEEE Trans Inf Theory. 2006. 52(5):1289–1306.
11. Jung H, Ye JC, Kim EY. Improved k-t BLAST and k-t SENSE using FOCUSS. Phys Med Biol. 2007. 52(11):3201–3226.
12. Jung H, Sung K, Nayak KS, Kim EY, Ye JC. k-t FOCUSS: a general compressed sensing framework for high resolution dynamic MRI. Magn Reson Med. 2009. 61:103–116.
13. Winkelmann S, Schaeffter T, Koehler T, Eggers H, Doessel O. An optimal radial profile order based on the Golden Ratio for time-resolved MRI. IEEE Trans Med Imaging. 2007. 26(1):68–76.
14. Poor HV. An Introduction of Signal Detection and Estimation. 1994. 2nd ed. New York: Springer-Verlag.
15. Liang Z. Spatiotemporal Imaging with Partially Separable Functions. 2007. In : 4th IEEE International Symposium on Biomedical Imaging: From Nano to Macro; 988–991.
16. Mistretta C, Wieben O, Velikina J, Block W, Perry J, Wu Y, Johnson K, Wu Y. Highly constrained backprojection for time-resolved MRI. Magn Reson Med. 2006. 55(1):30–40.
17. O'Halloran RL, Wen Z, Holmes JH, Fain SB. Iterative projection reconstruction of time-resolved images using highly-constrained back-proejction (HYPR). Magn Reson Med. 2008. 59(1):132–139.
18. Wild J, Paley M, Kasuboski L, Swift A, Fichele S, Woodhouse N, Griffiths P, van Beek E. Dynamic radial projection MRI of inhaled hyperpolarized 3 He gas. Magn Reson Med. 2003. 49(6):991–997.
19. Liang ZP, Lauterbur PC. Principles of magnetic resonance imaging: A signal processing perspective. 2000. New York: IEEE press.
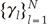 and
and 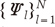 are the eigenvalues and the corresponding orthonormal eigenvectors of C (14). Then, the original signal σk can be represented as follows (14):
are the eigenvalues and the corresponding orthonormal eigenvectors of C (14). Then, the original signal σk can be represented as follows (14):
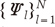 and coefficients
and coefficients 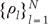 correspond to the sparsifying transform Ψ and unknown sparse signal ρ in Eq. [1], respectively.
correspond to the sparsifying transform Ψ and unknown sparse signal ρ in Eq. [1], respectively.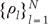 while the time variation in the process is embodied in the deterministic functions
while the time variation in the process is embodied in the deterministic functions 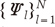 (14). Therefore, if each pixel of CE-MRA has similar behavior along temporal direction, we can represent the temporally varying images very sparsely with a small amount of randomness.
(14). Therefore, if each pixel of CE-MRA has similar behavior along temporal direction, we can represent the temporally varying images very sparsely with a small amount of randomness.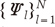 can be estimated using eigenvector decomposition of C as in Eq. [7]. Here, it is important to note that even though KLT bases are obtained from low spatial resolution images, the temporal changes are not smoothed at all because the resultant basis is complete in CN and we can represent any temporal variation in CN with linear combination of KLT bases. Therefore, the only concern about the approximated KLT bases is if the unknown signal can be represented with sparse coefficients ρ. We confirmed that the resultant coefficients are sparse enough in the following experiments. This is one of the main differences from partially separable function (PSF) approach (15), where only l significant principle components are used for temporal transform by assuming that the rank of the unknown x-t images is l. However, in real cases, it is hard to know the rank of the unknown x-t images a priori. In contrast, in our approach, the bases are complete and the sparse non-zero coefficients are obtained using l minimization.
can be estimated using eigenvector decomposition of C as in Eq. [7]. Here, it is important to note that even though KLT bases are obtained from low spatial resolution images, the temporal changes are not smoothed at all because the resultant basis is complete in CN and we can represent any temporal variation in CN with linear combination of KLT bases. Therefore, the only concern about the approximated KLT bases is if the unknown signal can be represented with sparse coefficients ρ. We confirmed that the resultant coefficients are sparse enough in the following experiments. This is one of the main differences from partially separable function (PSF) approach (15), where only l significant principle components are used for temporal transform by assuming that the rank of the unknown x-t images is l. However, in real cases, it is hard to know the rank of the unknown x-t images a priori. In contrast, in our approach, the bases are complete and the sparse non-zero coefficients are obtained using l minimization.



 PDF
PDF ePub
ePub Citation
Citation Print
Print


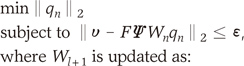
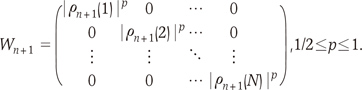
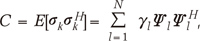
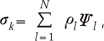




 XML Download
XML Download