This article has been
cited by other articles in ScienceCentral.
Abstract
Background
Measurement uncertainty characterizes the dispersion of the quantity values attributed to a measurand. Although this concept was introduced to medical laboratories some years ago, not all medical researchers are familiar with it. Therefore, the evaluation and expression of measurement uncertainty must be highlighted using a practical example.
Methods
In accordance with the procedure for evaluating and expressing uncertainty, provided by the Joint Committee for Guides in Metrology (JCGM), we used plasma glucose (Glu) as an example and defined it as the measurand. We then analyzed the main sources of uncertainty, evaluated each component of uncertainty, and calculated the combined uncertainty and expanded uncertainty with 2 budgets for single measurements and continuous monitoring, respectively.
Results
During the measurement of Glu, the main sources of uncertainty included imprecision, within-subject biological variance (BVw), calibrator uncertainty, and systematic bias. We evaluated the uncertainty of each component to be 1.26%, 1.91%, 5.70%, 0.42%, and -2.87% for within-run imprecision, between-day imprecision, BVw, calibrator uncertainty, and systematic bias, respectively. For a single specimen, the expanded uncertainty was 7.38% or 6.1±0.45 mmol/L (κ=2); in continuous monitoring of Glu, the expanded uncertainty was 13.58% or 6.1±0.83 mmol/L (κ=2).
Conclusions
We have demonstrated the overall procedure for evaluating and reporting uncertainty with 2 different budgets. The uncertainty is not only related to the medical laboratory in which the measurement is undertaken, but is also associated with the calibrator uncertainty and the biological variation of the subject. Therefore, it is helpful in explaining the accuracy of test results.
Keywords: Measurement uncertainty, Glucose, Quality control
INTRODUCTION
Error and error analysis have long been a part of practice in medical laboratories. The classic error theory comprises random error and systematic error. The random error is the component of measurement error that, in replicate measurements, varies in an unpredictable manner, whereas the systematic error is the component of measurement error that, in replicate measurements, remains constant or varies in a predictable manner [
1]. Thus, the random error can be estimated using frequency-based statistics, but the systematic error cannot be estimated using statistical methods. Therefore, error analysis, which includes statistical and non-statistical procedures, leads to inconsistencies in data analysis, particularly in error propagation [
2]. Additionally, it is impossible to measure a routine specimen more than a certain number of times in a medical laboratory. Therefore, the classic theory of error is no longer suitable for the actuality of laboratory medicine.
Measurement uncertainty is a non-negative parameter characterizing the dispersion of the quantity values being attributed to a measurand [
1]. Although introduced in the 1960s, the evaluation and expression of measurement uncertainty were only generally accepted in the 1990s. The medical community is not yet familiar with this new concept [
3]. When faced with the requirements of accreditation, medical laboratory researchers are unsure how to evaluate the uncertainty of measurement. Meanwhile, numerous studies have debated its practical application [
4-
6]. For example, there are no accepted criteria for which components should be introduced into measurement uncertainty. Therefore, training and explanations are necessary to introduce this concept into routine practice [
3].
Plasma glucose (Glu) is an important laboratory marker for diabetes mellitus. Clinical doctors and patients pay close attention to the concentration of Glu. In this study, the mea-surement of Glu was used as an example to demonstrate the procedure of evaluating uncertainty, and 2 budgets have been designed to combine the measurement uncertainty according to different measurement purposes.
MATERIALS AND METHODS
1. Materials
A Roche automatic biochemical analyzer (DDP; Roche Diagnostics, Penzberg, Germany) was used. Reagents, control materials, and the calibrator for Glu were also from Roche Diagnostics. The control materials were measured for the imprecision data. The proficiency test was organized by the College of American Pathologists (CAP). Biological variation documentation was obtained from the Westgard website [
7].
2. Evaluation methods
1) Definition of the measurand
From January to September 2010, plasma Glu was measured by the glucose hexokinase method in our laboratory, which was accredited by ISO 15189 (Certification Number: CNAS MT0034).
2) Identifying the sources of uncertainty
The main sources of uncertainty are analyzed in
Fig. 1 and are shown to come from pre-analysis and analysis.
(1) Pre-analysis
In pre-analysis, the sources of uncertainty included subject preparation, specimen collection, storage, and centrifugation. In the medical laboratory, the within-subject biological variance (BV
w) of the subject is an important source and should not be neglected for individuals whose Glu is continuously monitored. We obtained the BV
w data from the Westgard website [
7]. However, in cases where there was a single specimen, no BV
w could be calculated. The process of specimen preparation and storage could influence the result of the measurement. However, these factors can be reduced to a minimum by strictly executing the standard operating procedure.
(2) Analysis
Before measurement, the measurement system must be calibrated. According to the traceability reports, the measurement of Glu traces to the reference method of isotopedilution mass spectrometry (ID-MS). Because different levels of uncertainty in the calibrator will give rise to different uncertainty results, this uncertainty was evaluated as type B according to the uncertainty report provided by the manufacturer. Additionally, systematic bias is a factor affecting the accuracy of measurement. We evaluated the uncertainty of systematic bias according to the reports of the CAP proficiency test.
In the analytical process, many components of uncertainty, such as the repeatability of the absorbance, the stability of room temperature and humidity, and changes of operator and reagent lots, were involved. Fortunately, all these could be represented by imprecision. As shown in
Fig. 1, we calculated the within-run imprecision and between-day imprecision to represent the uncertainty caused by these factors.
3) Evaluation of the component of uncertainty [µ(χi)]
(1) Type A evaluation
According to the International Vocabulary of Metrology (VIM), type A evaluation is based on a statistical analysis of measured quantity values obtained under defined measurement conditions [
1]. Among all the above sources of uncertainty, the uncertainty of within-run imprecision [µ(χ
within-run)] and between-day imprecision [µ(χ
between-day)] belong to type A.
(2) Type B evaluation
According to VIM, type B evaluation is determined by means other than a type A evaluation [
1]. Type B includes the following sources of uncertainty. (i) BV
w: the data was quoted from the Westgard website [
7] and the uncertainty [µ(χ
BVw)] was calculated. (ii) Calibrator: according to the report of traceability and uncertainty provided by Roche Diagnostics, when the calibrator value of Glu was 10.70 mmol/L, the uncertainty was 0.0905 mmol/L (κ=2). We calculated the uncertainty [µ(χ
calibrator)] according to the data. (iii) Systematic bias: according to EP-15A [
8], the regression equation was constructed between the means of the proficiency test and the results of our lab (10 CAP survey data points, twice in 2010). Because the intercept denotes the fixed errors, we obtained the systematic bias [µ(χ
bias)] by setting the intercept as zero.
4) Determination of the combined uncertainty [µc(y)]
After evaluating each component of uncertainty [µ(χ
i)], all the components were combined. The combined uncertainty [µ
c(
y)] is equal to the positive square root of a sum of terms [
1], and the combined standard uncertainty of Glu should be calculated as shown below:
µc(Glu)=[µ2(χwithin-run)+µ2(χbetween-day)+µ2(χBVw)+µ2(χcalibrator)+µ2(χbias)]1/2
In this study, because all the components of uncertainty were relative quantities, we changed the computational formula as follows:
There is no agreement on whether BVw should be combined in a medical laboratory. According to the different purposes of measurement, we designed 2 budgets to combine the standard uncertainty. For a single specimen, budget 1 included imprecision, calibrator uncertainty, and bias; for those individuals who required consecutive monitoring, the BVw should be added as budget 2.
5) Calculation of the expanded uncertainty (U)
According to VIM, the expanded uncertainty (
U) equals to the product of a combined uncertainty and a coverage factor (κ) larger than the number 1 [
1]. In medical laboratories, κ is generally set to 2, which is associated with a coverage probability of 95%. So
U(
Glu)=2×µ
c(
Glu).
RESULTS
1. The components of uncertainty
1) Type A
According to the results of the within-run imprecision analysis, the µ(χwithin-run) was calculated as 1.26% (mean=6.77 mmol/L, n=20). Moreover, the µ(χbetween-day) was 1.91% (me-an=6.71 mmol/L, n=20).
2) Type B
The components of type B included BV
w, calibrator unce-rtainty, and bias. The sources and uncertainty of each component are listed in
Table 1.
2. The combined uncertainty
1) Budget 1
For a single specimen, the BVw component was not taken into consideration; therefore, the computational formulation for combined uncertainty was:
µC(Glu)=[1.262+1.912+0.422+(-2.87)2]1/2=3.69%
2) Budget 2
The BVw was added, and the computational formulation for combined uncertainty was changed to
µC(Glu)=[1.262+1.912+5.72+0.422+(-2.87)2]1/2=6.79%
3. The expanded uncertainty
According to the characteristics and requirements of the medical laboratory, we set the coverage factor (κ) to 2 with a coverage probability of 95%. Therefore, U=µc(Glu)×κ.
In this study, in order to combine the components of uncertainty, the relative uncertainty was used initially, and the expanded uncertainty was thus the relative expanded uncertainty (Urel). Generally, since patients and doctors pay great attention to the upper limit of a reference interval, we took 6.1 mmol/L as an example to calculate the expanded uncertainty (U). For budget 1, Urel=3.69%×2=7.38%, or U=6.1 mmol/L×7.38%=0.45 mmol/L; for budget 2, Urel=6.79%×2=13.58%, or U=6.1 mmol/L×13.58%=0.83 mmol/L.
We have listed all the uncertainties in this study in
Table 2.
DISCUSSION
The development of measurement uncertainty has come a long way. In 1963, the National Institute of Standards and Technology (NIST) suggested that the uncertainty should be expressed in quantitative methods, but no more detail on usage and expression was provided. In 2008, the Working Group 1 of the JCGM (JCGM/WG1) published the latest version of the Guide to the Expression of Uncertainty in Measurement (GUM), and it became the conventional standard for expressing the uncertainty of measurement [
9]. However, the concept of uncertainty is still relatively new in the field of quantity measurement, particularly in the medical laboratory. Therefore, in the present study, we have highlighted the evaluation and expression of uncertainty using a practical example.
With the development and standardization of clinical medicine, doctors and patients are expecting high-quality test results, which is a challenge to the medical laboratory. The measurement uncertainty may assist in facing this challenge; however, the process of measurement has been restricted by multiple factors such as reference measurements, the values assigned to the calibrator, the methods of calibration, and the preparation of subjects, not all of which can be controlled in a medical laboratory. These factors have evoked a dispute regarding the use of uncertainty in medical laboratories. Some experts in laboratory medicine have even expressed doubt regarding the applicability and usefulness of uncertainty in routine tests carried out by medical laboratories [
4,
5].
In this study, we chose the measurement of Glu to demonstrate the application of uncertainty in routine tests. Following the evaluation procedures recommended by JCGM [
9], we identified the sources of uncertainty and evaluated the components as type A and type B. While identifying the source of uncertainty, we took into account the accuracy of values assigned to the calibrator, because occasionally, the calibrator lot change leads to the violation of inner quality control. With regard to the physiological variation within an individual, this is very important for diabetics who require consecutive Glu monitoring. Consequently, we took the BV
w into consideration in budget 2. However, other potential uncertainty factors in pre- and post-analysis (for example, poor specimen collection or transportation, the pre-sence of drugs in the patient, and clerical and reporting errors), do not affect the inherent uncertainty of the testing procedure itself [
10], because we could control these factors well if all staff performed the tests in strict accordance with standard operating procedure. Therefore, these factors were excluded from the procedure for evaluating uncertainty.
The concentration of Glu is important for both endocrino-logists and diabetics, particularly when the concentration is close to the upper limit of the reference interval (6.1 mmol/L). We should apply different budgets of uncertainty to explain the accuracy and variation of Glu depending on the measurand. If the measurand is the plasma Glu taken from a patient at a specific time, then budget 1 is suitable. If the measurand is the plasma Glu taken from a patient who monitors his/her Glu concentration continuously over a time period, then the BVw becomes of interest, and budget 2 could be used, for example, if the specimen was from a patient taking the oral glucose tolerance test. In addition to the uncertainty, we should notify doctors and patients that κ=2 is generally associated with a coverage probability of 95%.
In summary, complying with the latest procedures provided by JCGM, we have demonstrated the overall process of evaluating uncertainty and designed 2 budgets to combine the uncertainty for different purposes. We hope that this can promote the use of measurement uncertainty in medical laboratories and can help doctors and patients to better understand the accuracy of results.
Acknowledgement
In this study, we thank Roche Diagnostics for the uncertainty report. Dr. Chun-hua Ding, at the University of California, San Francisco, provided great help in modifying the syntax of this article.
References
1. Working Group 2 of the Joint Committee for Guides in Metrology. JCGM 200:2008. International vocabulary of metrology: basic and general concepts and associated terms (VIM). 2008. 3rd ed. JCGM.
2. Ehrlich C, Dybkaer R, Wöger W. Evolution of philosophy and description of measurement (preliminary rationale for VIM3). Accred Qual Assur. 2007; 12:201–218.

4. Krouwer JS. Uncertainty intervals based on deleting data are not useful. Clin Chem. 2006; 52:1204. PMID:
16723686.

5. Krouwer JS. Critique of the guide to the expression of uncertainty in measurement method of estimating and reporting uncertainty in diagnostic assays. Clin Chem. 2003; 49:1818–1821. PMID:
14578312.

6. Kristiansen J. The guide to expression of uncertainty in measurement approach for estimating uncertainty: an appraisal. Clin Chem. 2003; 49:1822–1829. PMID:
14578313.
7. Westgard QC. Desirable specifications for total error, imprecision, and bias, derived from intra- and inter-individual biologic variation.
http://www.westgard.com/biodatabase1.htm. (Updated on Sep 2010).
8. National Committee for Clinical Laboratory Standards. User demonstration of performance for precision and accuracy: approved guideline. 2001. Wayne, PA: National Committee for Clinical Laboratory Standards.
9. Working Group 1 of the Joint Committee for Guides in Metrology. JCGM 100:2008. Evaluation of the measurement data: guide to the express of uncertainty in measurement. 2008. JCGM.
10. White GH, Farrance I. Uncertainty of measurement in quantitative medical testing: a laboratory implementation guide. Clin Biochem Rev. 2004; 25:S1–S24. PMID:
18650962.




 PDF
PDF ePub
ePub Citation
Citation Print
Print


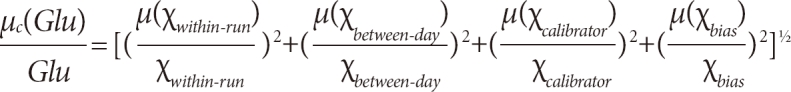
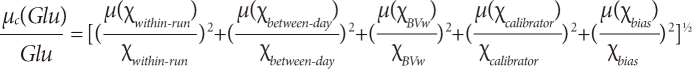



 XML Download
XML Download