Comparative Analysis of the Humphrey Static Perimetry and the Goldmann Kinetic Perimetry: Application of the Humphrey Static Perimetry to Visual Disability Evaluation

Jin Hee Shin; Song Hee Park

doi:10.3341/jkos.2013.54.12.1907

Journal List > J Korean Ophthalmol Soc > v.54(12) > 1009568

Go to TopGo to Top Go to BottomGo to Bottom

TOOLS

Shin and Park: Comparative Analysis of the Humphrey Static Perimetry and the Goldmann Kinetic Perimetry: Application of the Humphrey Static Perimetry to Visual Disability Evaluation

Original Article

J Korean Ophthalmol Soc 2013;54(12):1907-1917.

Published online: 7 September 2013

DOI: https://doi.org/10.3341/jkos.2013.54.12.1907

Comparative Analysis of the Humphrey Static Perimetry and the Goldmann Kinetic Perimetry: Application of the Humphrey Static Perimetry to Visual Disability Evaluation

Jin Hee Shin, MD, Song Hee Park, MD, PhD

Department of Ophthalmology, Soonchunhyang University College of Medicine, Seoul, Korea

Address reprint requests to Song Hee Park, MD, PhD Department of Ophthalmology, Soonchunhyang University Seoul Hospital, #59 Daesagwan-ro, Yongsan-gu, Seoul 140-743, Korea, Tel: 82-2-709-9354, Fax: 82-2-710-3196, E-mail: scheye@schmc.ac.kr

Received 19 April 201325 June 2013 Accepted 10 November 2013

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Purpose

In the evaluation of visual field defect, Goldmann kinetic perimetry is the preferred method. However, in many cases, Humphrey static perimetry is performed for visual disability evaluation in Korea. In the present study we investigated the correlation between Goldmann kinetic perimetry and Humphrey static perimetry for disability evaluation using visual field score (VFS).

Methods

This study included 126 eyes, classified into the following groups: 60 eyes, normal group; 11 eyes, contraction of central visual field group; 42 eyes, irregular visual field group; 13 eyes, hemianopsia group. All subjects were examined with Goldmann kinetic perimetry and Humphrey static perimetry. We studied the correlation of the VFS between Goldmann kinetic perimetry and Humphrey static perimetry according to the Korean Academy of Medical Science Guides for Impairment Evaluation (KAMS Guides) and American Medical Association Guides for the Evaluation of Permanent Impairment (AMA Guides).

Results

Regarding contraction of central visual field group, Goldmann VFS, Humphrey VFS and extended Humphery VFS showed no statistical significance (AMA: p = 0.50, p = 0.30, KMAS: p = 0.36, p = 0.18. respectively). In the irregular visual field and hemianopsia groups, Goldmann VFS and Humphrey VFS showed statistical significance (AMA: p = 0.00, p = 0.00, KMAS: p = 0.00, p = 0.00. respectively). Goldmann VFS and extended Humphrey VFS showed no statistical significance (AMA: p = 0.13, p = 0.12, KMAS: p = 0.08, p = 0.99. respectively).

Conclusions

The contraction of central visual field based on Humphrey static perimetry can be applied to visual disability evaluation. However, in the majority of cases, there is a difference between the two tests and Goldmann kinetic perimetry should be used first in the evaluation of visual field disability evaluation.

Keywords: Goldmann kinetic perimetry, Humphrey static perimetry, Visual field score

References

1. Schiller J, Paetzold J, Vonthein R. . Quantification of stato-ki-netic dissociation by semi-automated perimetry. Vision Res. 2006; 46(1-2):117–28.

2. Trobe JD, Acosta PC, Shuster JJ, Krischer JP. An evaluation of the accuracy of community-based perimetry. Am J Ophthalmol. 1980; 90:654–60.

3. Mills RP, Hopp RH, Drance SM. Comparison of quantitative test-ing with the Octopus, Humphrey, and Tübingen perimeters. Am J Ophthalmol. 1986; 102:496–504.

4. Beck RW, Bergstrom TJ, Lichter PR. A clinical comparison of vis-ual field testing with a new automated perimeter, the Humphrey Field Analyzer, and the Goldmann perimeter. Ophthalmology. 1985; 92:77–82.

5. Trope GE, Britton R. A comparison of Goldmann and Humphrey automated perimetry in patients with glaucoma. Br J Ophthalmol. 1987; 71:489–93.

6. Katz J, Tielsch JM, Quigley HA, Sommer A. Automated perimetry detects visual field loss before manual Goldmann perimetry. Ophthalmology. 1995; 102:21–6.

7. Heijl A, Drance SM. A clinical comparison of three computerized automatic perimeters in the detection of glaucoma defects. Arch Ophthalmol. 1981; 99:832–6.

8. American Medical Association. Guides to the evaluation of Permanent impairment. 5th ed.Chicago: AMA Press;2001. p. 267–94.

9. Korean Academy of Medical Science. Guides for impairment evaluation. Korea: Pakyoungsa. 2011; 81–95.

10. Chung SE, Lee SJ, Choi KS, Park SH. Comparison of the normal visual fields between the goldmann and humphrey kinetic perimetries. J Korean Ophthalmol Soc. 2009; 50:904–10.

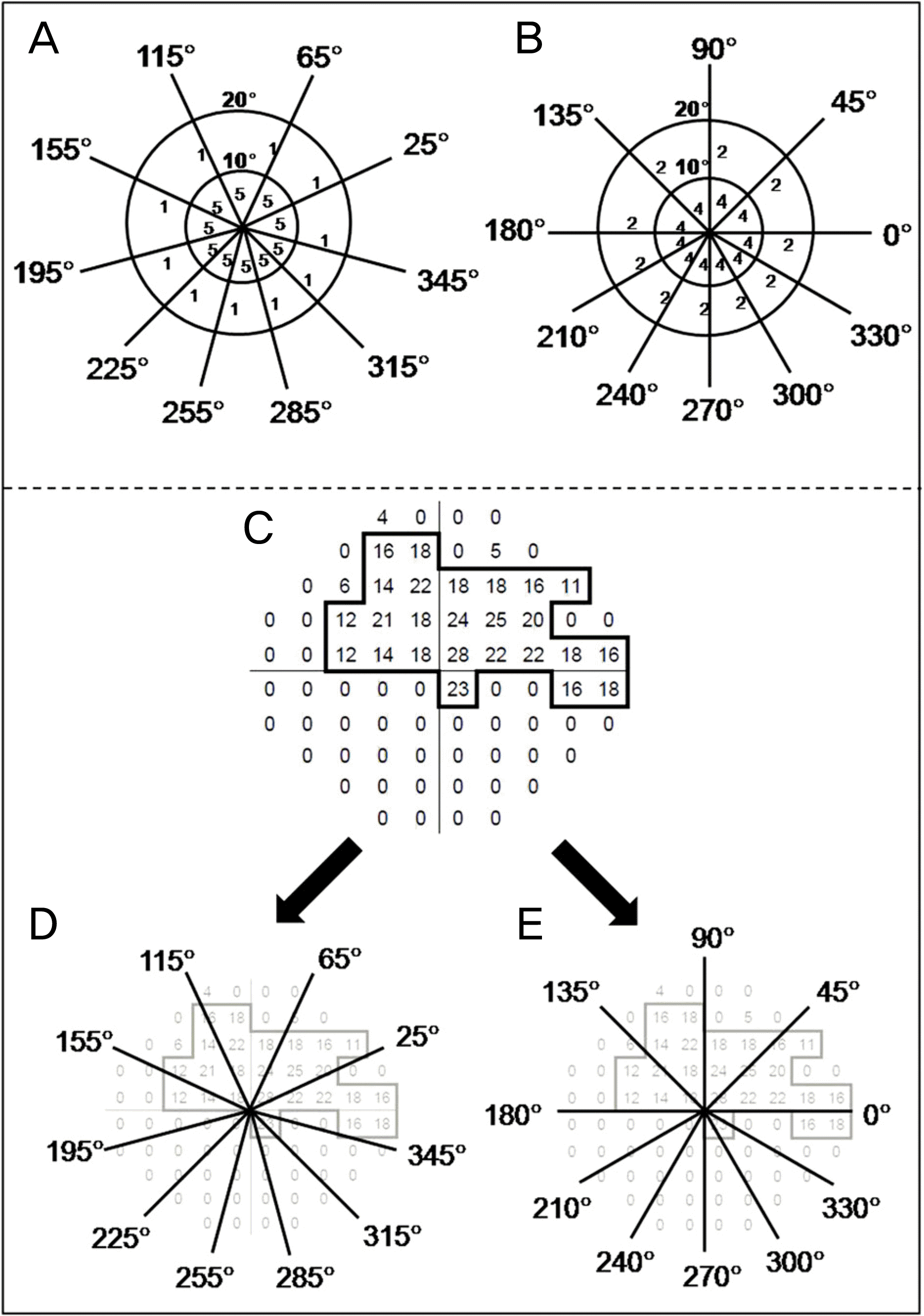Figure 1.

(A) The visual field score (VFS) calculated by American Medical Association’s Guides (AMA Guides, 2001, 5th edition). The testing grid is constructed by drawing 10 meridians (25°, 65°, 115°, 155°, 195°, 225°, 255°, 285°,315°, 345°). (B) The VFS calculated by Korean Academy of Medical Sciences’s Guides (KAMS Guides, 2011, 1st edi-tion). The testing grid is constructed by drawing 10 meridians (0°, 45°, 90°, 135°, 180°, 210°, 240°, 270°, 300°, 330°).(C) If only automated visual field plots are available, determine a pseudoisopter by drawing a line surrounding all points with a sensitivity of 10 dB or better, excluding points with <10 dB sensitivity. (D) The VFS calculated by AMA Guides, (E) The VFS calculated by KAMS Guides.

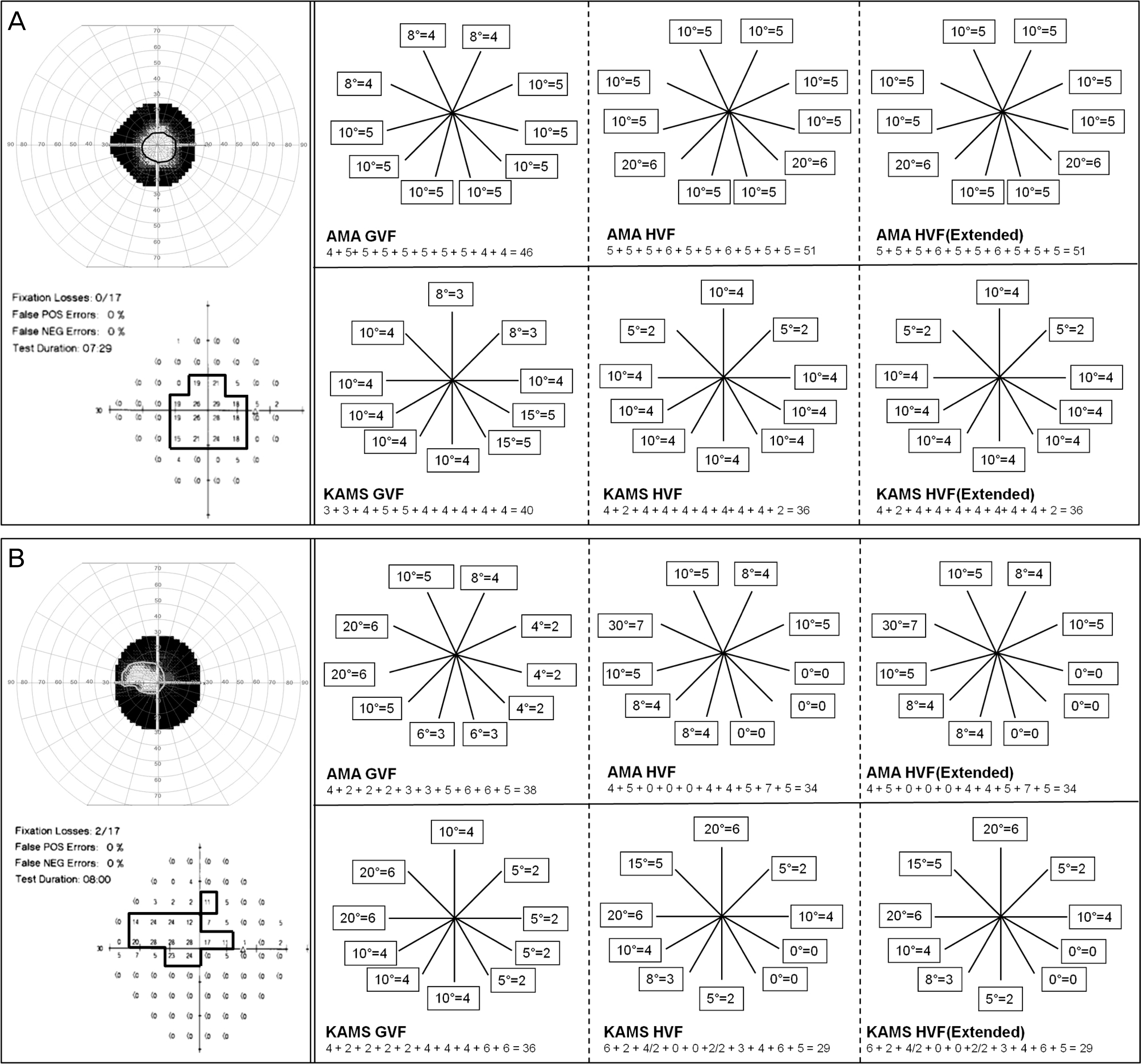Figure 2.

Central visual field groups. (A) 48-year-old, female, retinitis pigmentosa. Goldmann VFS is closely akin to Humphrey VFSs in both guides. (B) 48-year-old, male, after panretinal photocoagulation state due to proliferative diabetic retinopathy. Goldmann VFS is closely akin to Humphrey VFSs in both guides.

Figure 3.

Irregular visual field groups. (A) 68-year-old, male, glaucoma. Humphery VFSs are underestimated than Goldmann VFS in both guides. (B) 57-year-old, male, glaucoma. Humphery VFSs are underestimated than Goldmann VFS in both guides. (C) 75-year-old, male, glaucoma. Extended Humphery VFS is overestimated than Goldmann VFS.

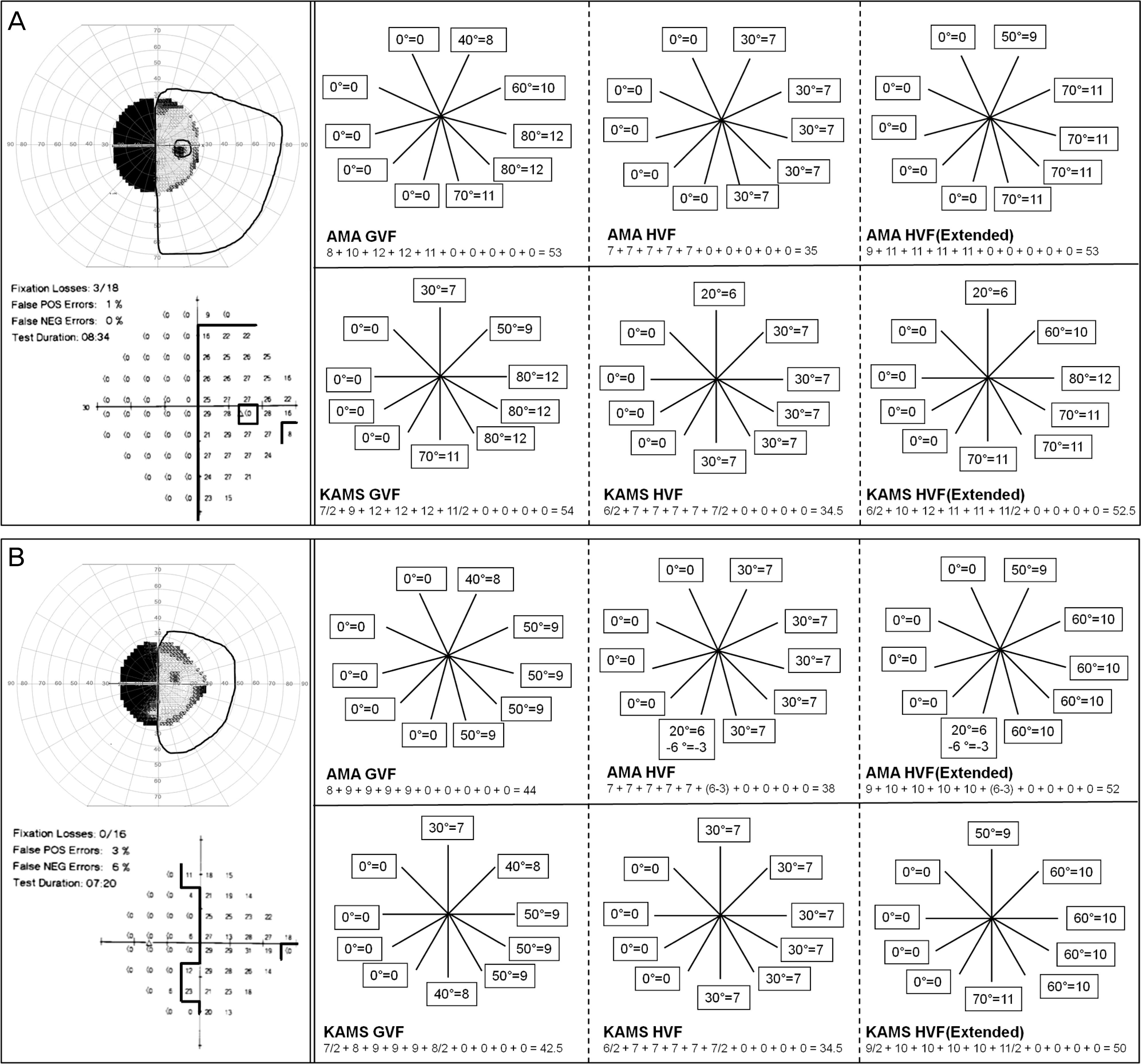Figure 4.

Hemianopsia groups. (A) 47-year-old, male, subarachnoid hemorrhage. Goldmann VFS is closely akin to extended Humphrey VFS in both guides. (B) 75-year-old, female, intracranial hemorrhage. Extended Humphrey VFS is overestimated than Goldmann VFS in both guides.

Table 1.

Diagnosis of visual field defect groups

Group (n)	Dignosis	No. of patients (HVF 30-2/24-2)
Central VF (11)	Retinitis pigmentosa	6 (4/2)
	After PRP state	4 (4/0)
	Panuveitis	1 (1/0)
Irregular VF (42)	Glaucoma	32 (26/6)
	Retinal detachment	3 (3/0)
	Opitc neuritis	3 (3/0)
	Branch Retinal Vein Occlusion	2 (2/0)
	Traumatic Optic Neuropathy	2 (2/0)
Hemianopsia (13)	Central Nervous System disease	13 (10/3)

VF = visual Field; PRP = panretinal photocoagulation; HVF = humphrey visual field.

Table 2.

Descriptive statistics for demographics and clinical characteristics of the study participants

Group (n)	Normal (n=60)	Central VF (n=11)	Irregular VF (n=42)	Hemianopsia (n=13)	p-value^*
Mean (age, years)	46.8 ± 14.6	53.6 ± 5.0	55.7 ± 16.1	41.2 ± 19.0	0.02
Sex (M:F, number)	36:24	5:6	30:12	7:6	0.21
CDVA (log MAR)	0.00 ± 0.00	0.19 ± 0.21	0.05 ± 0.11	0.00 ± 0.00	0.00
SE (D)	-1.13 ± 2.17	-0.92 ± 1.42	-0.64 ± 2.01	-0.84 ± 1.49	0.88
MD	-3.0 ± 1.9	-23.0 ± 6.5	-12.1 ± 6.0	-17.4 ± 2.7	0.00
PSD	2.2 ± 0.7	8.9 ± 3.2	9.4 ± 3.2	16.1 ± 1.9	0.00

Values are presented as mean ± SD.

VF = visual field; CDVA = corrected distance visual acuity; log MAR = logarithm of the minimum angle of resolution; SE = spherical equivalence; D = diopter; MD = mean deviation; PSD = pattern standard deviation.

^* Statistical significances were tested by Oneway analysis of variances among groups.

Table 3.

Comparison between Goldmann and Humphrey visual field score by AMA Guides

Group	GVFS	HVFS (p-value^*)	Extended HVFS (p-value^*)
Normal	100.0 ± 0.0	70.0 ± 0.0	100.0 ± 0.0
Central VF	41.1 ± 15.6	38.3 ± 20.6 (0.50)	45.5 ± 21.7 (0.30)
Irregular VF	71.4 ± 19.6	56.1 ± 14.6 (0.00)	77.4 ± 21.7 (0.13)
Hemianopsia	54.0 ± 7.2	38.9 ± 6.2 (0.00)	55.5 ± 6.2 (0.12)

Values are presented as mean ± SD.

AMA = American medical association’s guides; GVFS = goldmann visual field score; HVFS = humphrey visual field score; VF = visual field.

^* Statistical significances compared with GVFS were tested by paired t-test.

Table 4.

Comparison between Goldmann and Humphrey visual field score by KAMS Guides

Group	GVFS	HVFS (p-value^*)	Extended HVFS (p-value^*)
Normal	100.0 ± 0.0	70.0 ± 0.0	100.0 ± 0.0
Central VF	35.9 ± 14.4	32.18 ± 22.2 (0.36)	42.1 ± 24.3 (0.18)
Irregular VF	72.1 ± 18.5	54.2 ± 14.9 (0.00)	76.7 ± 24.4 (0.08)
Hemianopsia	53.4 ± 8.1	37.4 ± 8.9 (0.00)	53.4 ± 8.9 (0.99)

Values are presented as mean ± SD.

KAMS = Korean academy of medical sciences’ guides; GVFS = goldmann visual field score; HVFS = humphrey visual field score; VF = visual field.

^* Statistical significances compared with GVFS were tested by paired t-test.

TOOLS

Similar articles