From February 2012 to July 2013, 46 aneurysms in 44 consecutive patients were treated with endovascular coiling (with or without stent-assisted technique) at our center. Retreated patients and those with incomplete image data were excluded. Hence we reviewed 38 aneurysms in 38 patients, of which 36 were ruptured aneurysms and two were unruptured. There were 23 male and 15 female patients with a mean age of 57 years (age range, 34-76). Six aneurysms were bi-lobed, and 32 were saccular.

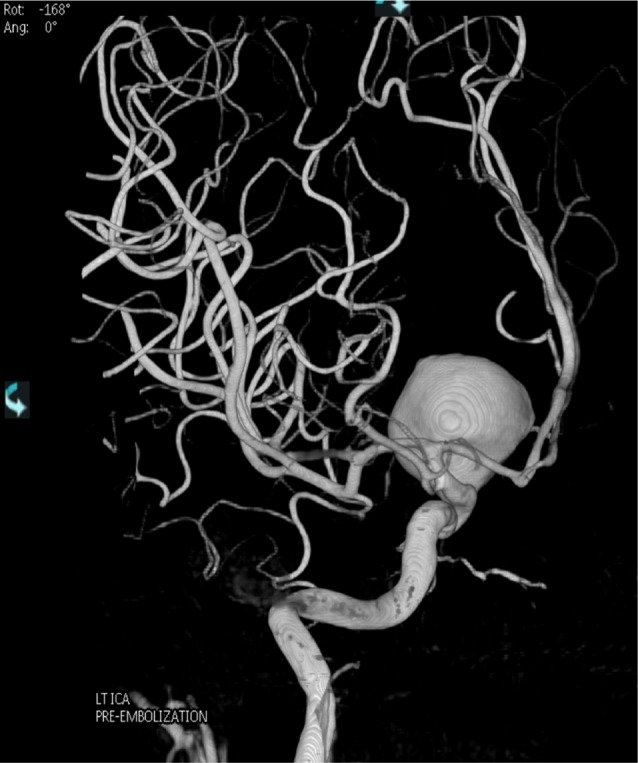
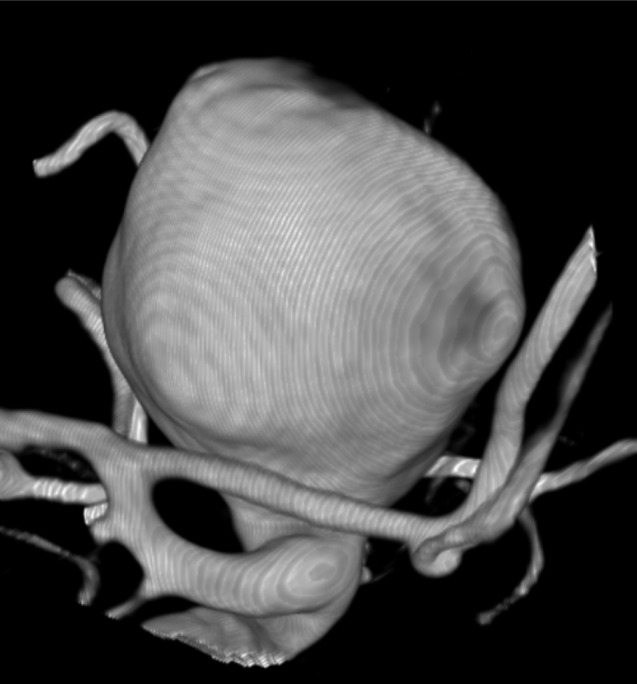
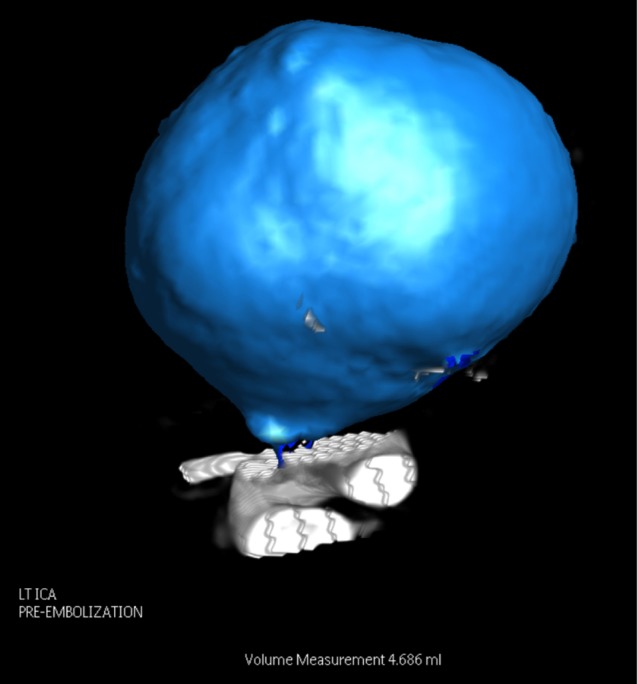
Neck size, height, width, and depth were measured using three-dimensional rotational angiography (3DRA). 3DRA images were acquired using an angiographic unit (Integris Allura Neuro; Philips Healthcare, Best, The Netherlands) and injection of a non-ionic contrast agent into an internal carotid artery or a vertebral artery. On a dedicated 3DRA workstation, the relevant cerebral vasculature was reconstructed and a three-dimensional "road-map" was acquired with a 256³ matrix. The aneurysm, with its parent vessels was first identified (Fig. 1) and outlined individually by a neurosurgeon who specialized in angiographic neuro-intervention, as well as by the primary author, a radiologist, for the purposes of segmentation. The histogram was standardized to default settings to eliminate inter-observer variability of aneurysm size. Next, using a "cut" tool provided by the workstation, the aneurysm was isolated from the parent vessels and related vasculature (Fig. 2). To ensure accuracy, the reconstructed and isolated aneurysm image would be viewed from different three-dimensional angles, before placing the automatic segmentation cursor over the perceived epicenter of the aneurysm. The computer workstation then proceeded with the interactive contouring based on isointensity surface extraction (ISE) and subsequent measurement of the aneurysm volume (Fig. 3). The isointensity surface is defined3) as the interface between the regions of the image I: I ≥ c (the inside), and I < c (the outside), where c is a constant intensity value, the surface is obtained by marching cubes method, where the points of the voxel cube are obtained by linear interpolation, producing a mesh with subvoxel accuracy, displayed with a measured aneurysm volume on the workstation. ISE and other forms of automatic segmentation have been previously reviewed and are known to have differed from the gold standard of manual segmentation within acceptable limits.3)

Geometric formulae were also applied for calculation of aneurysm volume. The shape of the aneurysm was first categorized according to "Sphere", "Ellipsoid", and "Bi-lobed". The mathematical calculations were as follows. The formulae of specific aneurysm configurations were defined as: "Spherical" volume equating to π/6 × diameter³; "Ellipsoid" volume equating to π/6 × width × depth × height; and "Bi-lobed" volume equating to the addition of the volumes of each of the two individual "ellipsoid lobes".

Aneurysm volumes were dichotomized according to two groups; those with a volume of less than 54 mm³ ("small" aneurysm, n = 20), a value corresponding to the median volume of all 38 aneurysms, and those with a volume of 54 mm³ or greater ("large" aneurysm, n = 18). This method of dichotomization was selected based on a previous study by Piotin et al.5) reviewing the relationship of aneurysm volumes and packing densities with angiographic recurrence that had employed similar research methodology.

Packing densities were also categorized accordingly; those with coil packing of less than 24% ("low packing") and those with packing of 24% or greater. This method of dichotomization was derived from the 2004 study by Sluzewski et al.,8) which noted that coiled aneurysms with packing densities of 24% or greater had no coil compaction at 6-month follow-up in their cohort.

Statistical analysis was subsequently performed using IBM SPSS software version 20 (IBM corp., Armonk, NY, USA). Volumes and relevant packing densities were compared between those measured by automatic segmentation against those measured by geometric formulae using the non-parametric Wilcoxon signed rank test. The number of aneurysms categorized as "large" and "small" volumes measured by the respective methods were compared and analyzed. p values of less than 0.05 were considered to indicate a statistically significant difference.

The median aneurysm volume (mm³) obtained was 54.5 by 3DRA (mean, 172.8; range, 5- 3527) and 30.6 by the geometric formulae (mean, 234.3; range, 4-6084). In application of 3DRA measurements, there were 18 large aneurysms (47.4%) and 20 small aneurysms (52.6%). In comparison, there were 14 large aneurysms (36.8%) and 24 small aneurysms (63.2%) when mathematical formulae were applied. Volumes were analyzed using the Wilcoxon signed rank test yielding a Z value of -1.646 (p = 0.1), r = 0.189 for the difference of values obtained by simple formulae when compared against 3DRA.

The median coil packing density (%) by 3DRA was 17.8% (mean, 21.6; range, 7.2-84.5) and 22.9 by the geometric formulae (mean, 32.4; range, 11.0-192.9). In application of 3DRA measurements, there were eight highly packed aneurysms (21.1%) and 30 with low coil packing density. In comparison, there were 14 highly packed aneurysms (36.8%) and 24 with low coil packing (63.2%) when mathematical formulae were applied. Coil packing densities were analyzed using the Wilcoxon signed rank test yielding a Z value of -3.053 (p = 0.002), r = 0.35 for the difference of values obtained by simple formulae when compared against 3DRA.

In their 2004 study Sluzewski et al.8) employed biplanar angiography for measurement of aneurysm volumes, analyzing the volumes of 145 aneurysms treated with coils and the relevant follow-up outcomes at 6 months post-treatment. Their results demonstrated that aneurysm volume, packing density, and compaction at 6 months follow-up were closely related and concluded that the common practice of inserting as many coils as possible to achieve a high packing density was sensible, and that high packing density was essential to preventing recurrence, as patients in their study with packing density of 24% or more had no coil compaction. They also noted that high packing density could not be achieved in larger aneurysms with high volumes of more than 600 mm³, which resulted in compaction in the majority of these aneurysms.

In contrast, in their 2007 review Piotin et al.5) published an opposite viewpoint on the issue regarding packing density. They retrospectively assessed the post-treatment angiography results of 255 aneurysms in 223 patients with a mean follow-up period of 12 months, dichotomizing them according to the presence or absence of recurrence. This group utilized 3DRA system software segmentation as the measurement tool of choice, but no specific details regarding the segmentation method were discussed. Their results showed that both recurring and stable aneurysms had a mean packing density of 27%, concluding that more angiographic recurrences would be detected over time, and that packing density was not related to protection against recurrence.

It is notable that both groups employed different methods of volume measurement, which largely affect the resultant measured packing density. 3DRA has been increasingly utilized as the main technique of choice for measurement of related geometric indices and configurations in later studies.6) Increased accuracy, improved resolution of images, better evaluation of anatomy and enhanced treatment planning1) were observed in 3DRA compared to previous methods of volumetric measurement, which included mathematical equations and bi-planar digital subtraction angiography.7)

Our study showed that there were a greater number of "small" aneurysms when geometric formulae were used as compared to automatic segmentation, although this underestimation was not statistically significant. More aneurysms were also categorized as being "highly packed" when mathematical formulae were applied (p = 0.002). Indeed, some of the packing densities calculated from the formulae exceeded 100% due to the gross underestimation of cerebral aneurysm volumes. This may reflect inherent inaccuracies in the use of these equations due to the irregularities of aneurysm shapes and the presence of various configurations such as blebs and daughter-sacs.

The majority of the aneurysms included in this study were ruptured (i.e. 36 out of the 38 aneurysms analyzed). Indeed, ruptured aneurysms often have a bleb or daughter sac that may have an effect on the measurement of aneurysm volume. This could account for the consistent underestimation of volumes when measured using geometric formulae, being unable to account for the additional volume while automatic segmentation has the ability to detect this particular configuration.

The relatively consistent overestimation of coil packing density in the treated patient may then confer the neuro-interventionist a false sense of security in terms of technical success and a possibly varied prognosis for aneurysm recurrence. Although the idea of simple geometry may seem attractive as previously discussed, it remains a poor model for establishing aneurysm volumes.

Due to the lack of 3DRA images prior to 2012 at our center, our retrospective analysis included a restricted study population. In addition, wide-necked, bi-lobed and "small" aneurysms occasionally presented difficulty in digital volume reconstruction and detection by the incorporated software. The edges of the segmented aneurysm were often not well delineated, demonstrating the problem of an "indented" aneurysm. Use of default window and histogram settings would occasionally result in an unregistered volume measurement, requiring several attempts before automatic detection could be made and hence prolonging user analysis time and affecting repeatability of results. Although these settings could be manually manipulated could be performed to enhance the appearance and outline of the aneurysm image to aid computer measurement, it was not carried out in this study, as it would then have erroneously translated to a significant fluctuation of aneurysm size and its related parent vessels.

Studies investigating packing density should describe in detail the arrival of aneurysm volume calculations with manual segmentation using 3DRA for better reproducibility and consistency. Further research should also focus on validating the assumption that automatic segmentation is truly superior in volume measurement compared to that of geometric formulae by analyzing phantom models. Improving the accuracy and precision of volume reconstruction and segmentation software and enhancing its application to clinical practice will also be of great interest. This would enable enhanced monitoring of coil packing density and determining its relation to coil compaction and aneurysm recurrence in future prospective studies.